纱筒残余氨的扩散过程建模与数值模拟
2017-09-25张东,孟婥
张 东, 孟 婥
(东华大学 机械工程学院, 上海 201620 )
纱筒残余氨的扩散过程建模与数值模拟
张 东, 孟 婥
(东华大学 机械工程学院, 上海 201620 )
为准确把握液氨整理后纱筒中残余氨的传质特性,提高氨的回收率与回收速率,首先建立了经综合考虑扩散传质和对流传质机制的传质数学模型,对柱坐标系下的传质方程进行归一化处理,将其转换成易于分析的一维平板类传质方程。然后利用Crank-Nicolson隐式差分法对归一化的传质方程进行差分近似求解,证明了算法的稳定性与收敛性。最后将数值计算结果与实验数据对比,验证模型的正确性。结果表明,提高风速以及减小纱筒外径都可加快氨的挥发,小风速下氨挥发过程是一个近似稳态过程。
纱筒; 残余氨回收; 液氨整理; 传质数学模型; 数值模拟
对氨和天然纤维材料之间的改性机制和工艺过程的大量深入研究证实了氨对天然纤维的改性作用具有显著效果[1]。纱筒从改性釜中改性取出后仍然有残余氨存在,因此,需对残余氨的扩散过程进行研究。
棉麻纤维纱线通常缠绕在筒芯上形成纱筒,纤维或纱线作为固体骨架,缠绕时的物理间隙形成纱筒内部孔隙,因此,纱筒是一种多孔材料,残留的液氨和气氨为流体填充在纱筒中。目前对多孔材料中流体传质过程特性的研究主要集中在一维平板类传热传质方面[2-4],鲜有对纱筒这种柱状多孔材料传质特性的研究,并且柱坐标系下传质方程的解析解极其复杂,这给数学计算及工程应用带来极大困扰。
本文首先建立了基于传质学原理的纱筒传质数学模型,能够模拟纱筒中残余氨的散发行为,明确反映其物理过程。然后通过坐标变换使圆柱坐标系下的问题转换为平板问题,为圆柱状材料的传热传质提供计算方法。再利用隐式差分法近似求解传质方程,并证明算法的稳定性与收敛性。最后将数值模拟结果与实验数据作对比,对其传质特性进行分析,指出影响残余氨挥发速率的因素,以期为工程实践中准确预测纱筒残余氨挥发过程提供模型与计算方法。
1 纱筒传质模型
1.1模型的提出
多孔材料中流体挥发具有相当复杂的过程特性,现有研究多是根据流体力学基本理论和传质传热原理,对实际挥发过程进行简化,基于合理的假设条件建立数学模型,因此,对本文研究的改性后纱筒中残余氨的挥发过程做以下建模条件假设。
1) 纱筒中纱线层视为均质的等效圆柱体多孔材料,且只考虑该等效圆柱体内部扩散和表面对流扩散[5]。2) 圆柱体内的扩散是由纱线层内不同位置处液氨浓度差引起的,由于回收残余氨过程中纱筒是首尾相接逐个堆砌的,故只考虑圆柱体内径向一维扩散,忽略轴向扩散。采用等效扩散系数代替径向扩散系数。3) 假定纱层圆柱体表面存在一个界限层,该界限层靠近纱层一侧,以液相状态存在;靠近空气流一侧,残余氨以气相状态存在。在界限层处液相氨和气相氨发生相变,并处于平衡状态,液相浓度和气相浓度分配关系服从亨利定律[5]。4) 初始时刻,纱线层内氨浓度是均匀的。5) 挥发过程中纱线层温度和空气流温度均视为不变,整个过程中氨的质量传输是连续的。
1.2残余氨挥发模型的建立
由建模假设条件,根据多相传质基本理论并结合纱筒的物理结构形式,建立纱线中残余氨挥发模型,如图1所示。
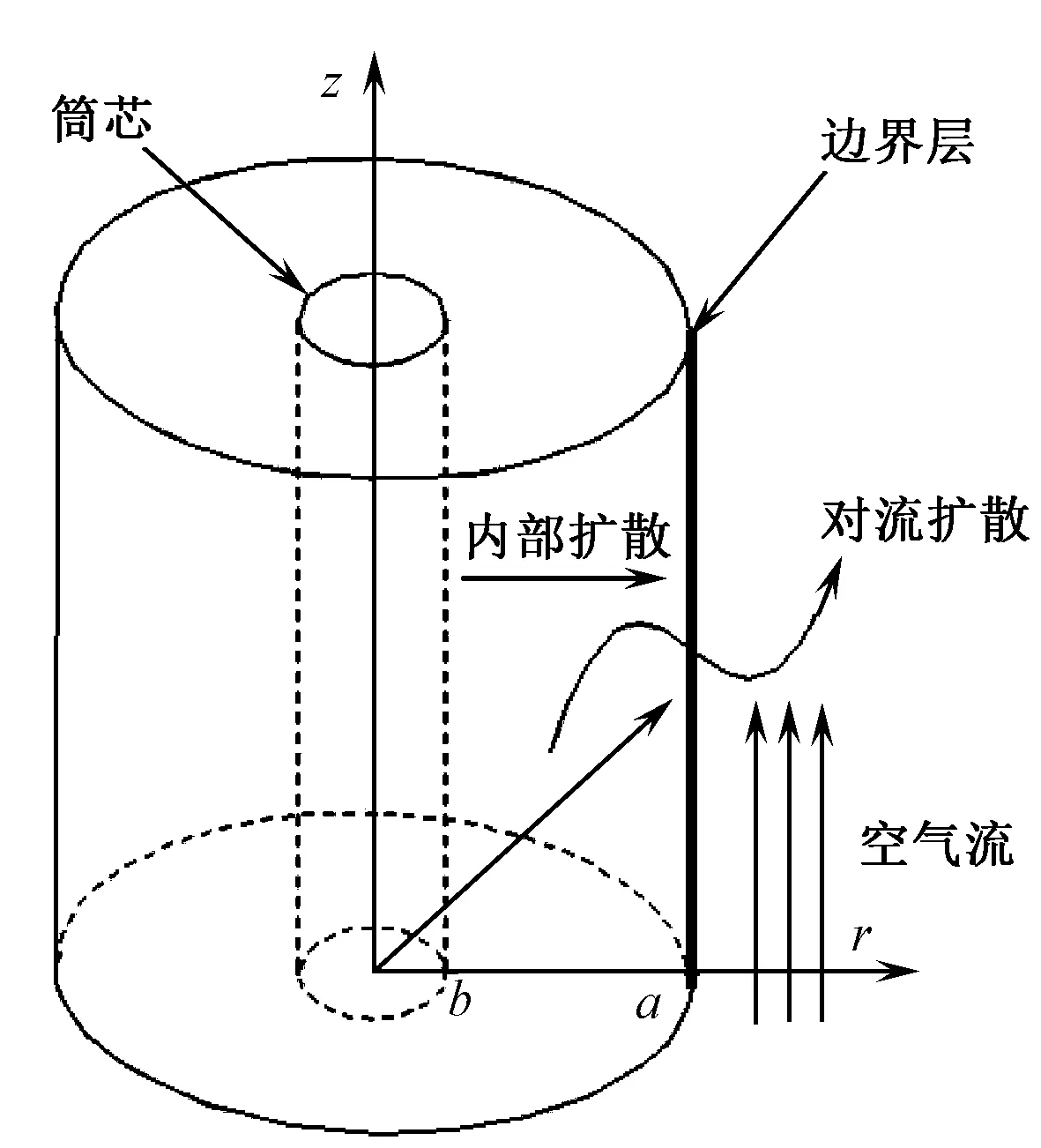
图1 纱筒传质模型Fig.1 Model of mass transfer
纱筒简化为空心圆柱体,以纱筒底面中心为原点,沿轴向和径向建立柱坐标系,纱层位于内外半径为a和b的同心环形体内,纱筒外部为空气流,其流动方向与纱层表面平行,且纱筒圆柱体表面各位置处的空气流流速及方向相同,由于是数个纱筒堆砌放在改性釜中,可忽略上表面及下表面空气流作用。纱层表面与外界空气流之间存在边界层,纱层内液相氨以扩散方式向边界层传输,在边界层内液相氨转化为气相氨,并在边界层外侧通过对流扩散方式扩散到空气流中。如图1所示,残余氨挥发模型将纱筒中氨挥发过程描述为由纱层到边界层到空气流层的3层结构传质体系,其中边界层内通过动态吸附脱附作用在纱层表面形成液相氨与气相氨的浓度分配,实现内部扩散与外部对流扩散之间物质传输过程的衔接。
1.3数学模型的建立
扩散传质区内,r=a处为纱层与筒芯交界面,在筒芯侧液氨浓度梯度为零,纱层侧液氨浓度为ρ(r,t),简记为ρ。其扩散由浓度梯度与等效扩散系数D决定,故由菲克第二定律知,纱层内传质控制方程[6]为
(1)
式中:ρ为氨的质量浓度,kg/L;r为散发方向的坐标,m;t为传质经历的时间,s。
由假设条件5可知,纱层扩散初始条件为
ρ|t=0=ρ0
(2)
边界层指纱筒和空气的接触面,厚度可忽略,层内氨浓度由纱层到空气发生骤降,存在动态吸附平衡,控制方程边界条件为
(3)
式中:a为纱筒外径,m;b为纱筒的内径,m;ρ∞为空气流中氨的质量浓度,kg/L;D为等效扩散系数,m2/s;k为空气中氨的对流扩散系数,m/s;β为氨在纱筒和空气交界面处的浓度分配系数,为无量纲数。
1.4归一化处理
由于1.3中建立的数学模型难以用有限差分法进行数值计算,并且不易确定算法的精度与稳定性,因此,为了能与平板类传质方程相类比、分析问题的本质,必须要转换成直角坐标的数学方程,令

(4)

(5)
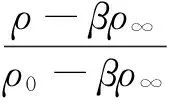
(6)
式中:T为无量纲时间;X为无量纲坐标;C为无量纲质量浓度。且T≥0,0≤X≤1,0≤C≤1,对式(4)~(6)进行坐标变换得

(7)
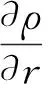
(8)
(9)
将式(7)~(9)代入式(1),得到归一化的纱筒内扩散控制方程
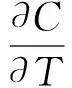
(10)
同理可得归一化的初始条件为
C|T=0=1
(11)
内边界条件为
(12)
外边界条件为
(13)
自此,已将模型中的物理方程进行了归一化处理,为后面验证算法稳定性与收敛性奠定了基础。
2 传质方程离散化
传质方程(1)的解析解求解比较复杂[7],在工程实践中不易计算,本文采用有限差分法求解式(10),使其更具实用性。式(10)是抛物线型偏微分方程,其影响域为半域,宜采用中心差分计算。将0≤X≤1等分成N份,从而△X=N-1,Xi=i△X,Tn=n△T,C(Xi,Tn)=C(i△X,n△T)简记为Cin,下标i代表第i空间层,上标n代表第n时层,在数值计算中Cin即是节点(i,n)的数值。为了使式(10)对时间和空间都具有二阶精度,采用对网格点(n,n+0.5)进行中心差分计算,得到式(10)的相容性隐式差分方程,如式(14)所示。
(14)
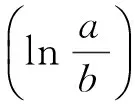
(15)
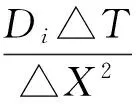

(16)
即得到内边界条件。同理假设外虚拟点CN+1,由式(13)得:
(17)
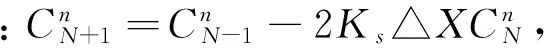
将其代入式(15)中得到外边界条件:
(18)
综合式(15)、(16)、(18)得到时间推进方式的代数方程组
C(n)=A-1BnC(0)
(19)
式中:

A、B为N+1阶三对角方阵;C(n+1)、C(n)为N+1维向量。
由Von Neumann分析法即傅里叶分析法知,差分格式的误差放大系数[8]为
即g≤1
式中,θ为相邻2个节点上的谐波相位角之差,rad。从而可知式(14)的差分格式是稳定的,由Lax定理可知差分格式也是收敛的[8]。三对角阵A满足优对角条件,代数方程组(19)的解亦恒稳定,可取较大时间步长,计算省时,精度也满足要求。通过解方程组(19)便可得出氨的浓度随位置与时间的变化规律,再通过高精度数值积分,便可获得任意时刻纱筒内剩余氨的质量,可与实验数据作对比,验证模型和算法的合理性。
3 传质参数确定
3.1扩散系数与分配系数
扩散系数D与纱筒内纱线的组织结构、缠绕方式以及松紧程度等因素相关。分配系数β描述了在纱筒边界层液相氨与气相氨的比例关系,其中D和β的取值可参考文献[9],D=1.777 8×10-6m2/s,β=8 340。
3.2对流扩散系数
由对流传质Sherwood(Ss)准数[10]知:
层流时Ss=0.664Sc1/3Re1/2(Re<500 000)
湍流时Ss=0.037Sc1/3Re4/5(Re>500 000)
式中:Sc=kzDa-1;雷诺数Re=uzv-1;z为纱筒高度,m;k为对流扩散系数;Da为氨在空气中的传质系数。
Da=D0P0Pair-1Tair3/2T0-3/2
式中:D0、P0、T0和Da、Pair、Tair分别是氨气在标准状态下和实验条件下的扩散系数、压强和温度;u是空气流流速,m/s;v是运动黏度,m2/s。由于Re<500 000,从而对流扩散系数为

当风速u=0.1 m/s时,k=2.3×10-3m/s;当u=0.5 m/s时,k=5.2×10-3m/s;当u=1 m/s时,k=7.3×10-3m/s。
4 数值计算结果
改性前称量纱筒,改性后再次称量纱筒,二者相差即为纱筒内残余氨的初始质量M0。将改性后的纱筒首尾相接堆砌放置在烘干炉中,在恒定温度(293 K,使传质系数都是常量)下,再调控风机风速,不同风速(u分别为0.1、0.5、1.0 m/s)条件下进行残余氨的回收,挥发出的氨气通入水中,再经过后处理回收氨。由于在持续通风条件下ρ∞≈0,每隔1 h称量1次,共称量20次,结果取平均值,获得了纱筒残余氨挥发速率曲线,将所得实验数据与数值计算结果作对比,结果如图2所示。
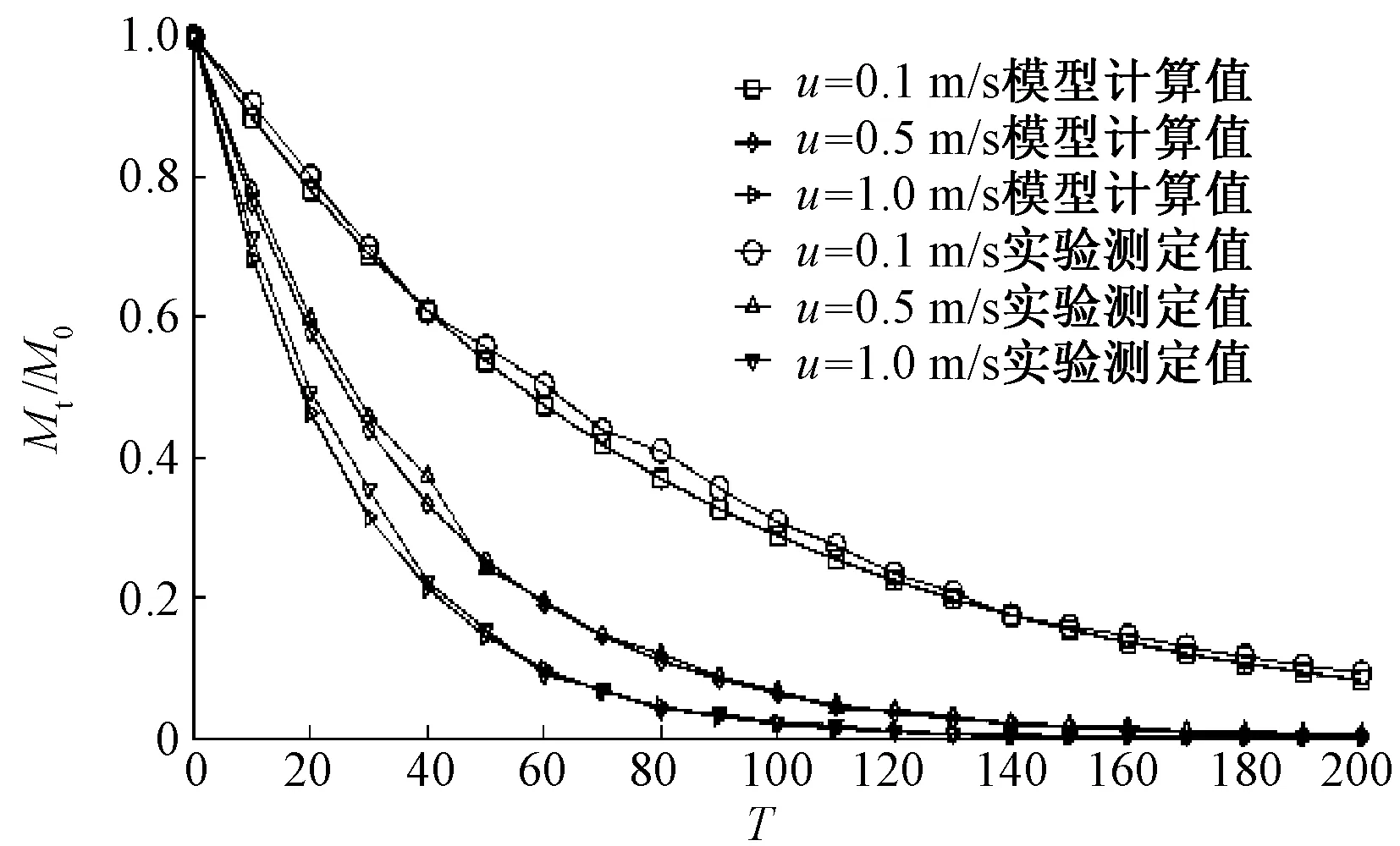
图2 实验结果与模拟结果对比Fig.2 Comparison between experimental data and calculated data
图2中M0是初始时刻纱筒中残余氨的质量,Mt是任意时刻纱筒中残余氨的剩余质量,纵坐标Mt/M0即是纱筒内残余氨与总传质质量之比。在开始一段时间内,仿真数据与实验数据有些偏差,主要原因是没有考虑传质速度的有限性[11],以及氨挥发时大量吸热,导致温度降低,挥发速率降低。在传质稳定后,传质速度有限性对扩散速率的影响可以不计,从而能很好地表达实际情况,故本文模型可作为工程实践的计算模型。从图还可看出,在开始的一段时间氨的剩余量下降得最快,表明挥发速率最快。
图3示出不同风速不同时间时纱筒内的归一化残余氨质量浓度,图中纵坐标C是无量纲质量浓度。可看出,提高风速可加快残余氨的挥发速率,但随着时间推移,挥发速率不断降低,这时单纯依靠提高风速来增加挥发速率已不可行,必须要提高环境温度等其他因素才能达到工程需求。故本文可为优化风速提供借鉴增加达到节能减排的效果。
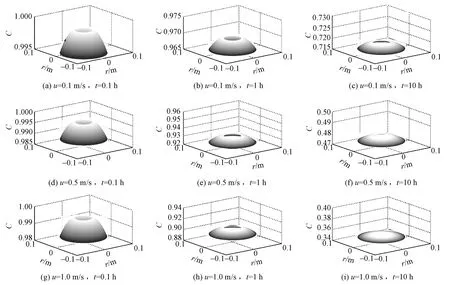
图3 不同风速和不同时间时纱筒内的归一化残余氨质量浓度Fig.3 Normalized concentration distributions under conditions of different air flow velocities and different time
图4示出不同时间不同位置处的浓度曲线。由图可知,在同一时刻纱筒内外的浓度差别是很小的,其原因是残余氨挥发过程是缓慢的,是一近似稳态过程,但当边界层挥发速度较快即风速极快时便不再是准稳态过程,必须要考虑到传质松弛时间的问题[11]。

图4 不同时间不同位置处的浓度曲线Fig.4 Concentration curves under conditions of different time and positions

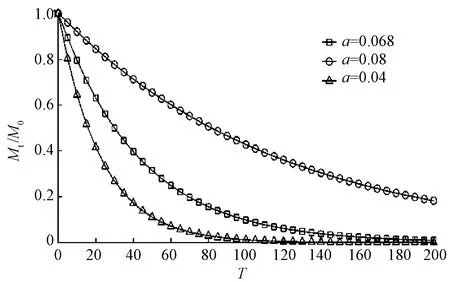
图5 不同纱筒外径下的传质速率曲线Fig.5 Mass transfer rate curves of different diameters
5 结 论
1)在综合考虑了二大传质机制条件下,建立了纱筒残氨挥发模型。通过对方程进行归一化处理使得柱状传质问题转变成了一维平板类传质问题,为柱坐标系下的传质问题提供了一种新的求解方法。
2)利用Crank-Nicolson隐式差分法对归一化的传质方程进行差分近似求解,证明了算法的稳定性与收敛性,并求得了与实验数据吻合很好的结果,验证了模型的正确性,可为工程实践提供借鉴。
3)通过对计算结果的分析可知,提高风速可加快氨的挥发,并指出了纱筒外径对氨挥发时间和风机空气流利用率的影响,为工程实践中优化纱筒外径提供了模型与计算基础。
FZXB
[1] 隽海艳, 孟婥, 孙以泽, 等. 改性处理对亚麻纤维形态结构和结晶度的影响[J].棉纺织技术, 2013, 41(7):499-501. JUAN Haiyan, MENG Zhuo, SUN Yize, et al. Effect modifiction on morphology and crystallinity of flax fiber[J]. Cotton Textile Technology, 2013, 41(7): 499-501.
[2] 宋伟, 孔庆媛, 李洪枚. 木家具表面挥发性污染物散发传质特性[J].化工学报, 2013, 64(5): 1550-1558.SONG Wei, KONG Qingyuan, LI Hongmei. Characteristics of VOC mass transfer from wood furniture surface[J]. CIESC Journal, 2013, 64(5): 1550-1558.
[3] 宋伟, 孔庆媛, 李洪枚. 建材VOC散发过程模拟与传质参数测定新方法[J].化工学报, 2013, 64 (3):913-922. SONG Wei, KONG Qingyuan, LI Hongmei. New method for simulation of VOC emission from building materials and measurement of mass transfer para-meters[J]. CIESC Journal, 2013, 64(3): 913-922.
[4] 林庚,倪文,于昕. 纳米孔真空绝热板一维稳定导热数学推导及其数值分析[J].中国矿业, 2008, 17(3):85-88. LIN Geng, NI Wen, YU Xin.Nonporous vacuum insulation panel one dimensional stable heat conduction mathematic deduction and numerical analysis[J]. Chinese Mining Industry, 2008, 17(3):85-88.
[5] RANA P, BHARGAVA R, BEG O A. Numerical solution for mixed convection boundary layer flow of a nanofluid along an inclined plate embedded in a porous medium[J]. Comput Math Appl, 2012,64(9):2816-2832.
[6] THORSTENSON D C, POLLOCK D W. Gas transport in unsaturated zones: multi-component systems and the adequacy of Fick′s laws[J]. Water Resources Research, 1989, 25(3):477-507.
[7] CRANK J. The Mathematics of Diffusion[M]. London: Clarendon Press, 1975:138-159.
[8] ANDERSON J D. Computational Fluid Dynamics: the Basics with Applications[M]. New York: McGraw-Hill, 1995:10-50.
[9] ZHU Helei, MENG Zhuo, SUN Yize, et al. Unsteady multi-phase mass transfer modeling and analysis for the process of the ammonia volatilization from yarn bobbin[J]. International Journal of Heat and Mass Transfer, 2016(103): 231-241.
[10] WHITE FM. Heat and Mass Transfer[M]. [S.l.]:Addison-Wesley, 1988:20-30.
[11] 淮秀兰,姜任秋. 快速瞬态传质过程中非菲克效应的实验与理论研究[J]. 工程热物理学报, 2000, 21(5):595-599. HUAI Xiulan, JIANG Renqiu. Theoretical and experimental study on the effect of the non-Fick in fast transient mass transfer process[J]. Journal of Engineering Thermophysics, 2000, 21(5):595-599.
Modelingandnumericalsimulationforresidualammoniavolatilizationfromyarnbobbin
ZHANG Dong, MENG Zhuo
(CollegeofMechanicalEngineering,DonghuaUniversity,Shanghai201620,China)
In order to accurately grasp the mass transfer characteristics of residual ammonia in yarn bobbins after liquid ammonia treatment and increase the recovery ratio and recovery rate of ammonia, a mathematical model of mass transfer was established by considering diffusion and convection. It became easier to analyze the mechanism of the emission of ammonia when the mass transfer equations was normalized. Then the Crank-Nicolson implicit difference method was used to solve the normalized mass transfer equations, and the stability and convergence of the algorithm were proved. Finally, the numerical results were compared with the experimental data, which proved the correctness of the model. The conclusion shows that the method of increasing wind velocity and decreasing the bobbin outer diameter can accelerate the volatilization of ammonia, and the ammonia volatilization process under low wind speed condition is an approximate steady state process.
yarn bobbin; residual ammonia recovery; liquid ammonia treatment; mathematical model of mass transfer; numerical simulation
TS 19
:A
10.13475/j.fzxb.20160903706
2016-09-21
:2017-06-16
长江学者与创新团队发展计划滚动支持项目(IRT_16R12);东华大学博士创新基金项目(16D310303)
张东(1989—),男,博士生。主要研究方向为流体及热质传递学。孟婥,通信作者,E-mail:mz@dhu.edu.cn。
