基于空间连通度的江南园林庭院空间研究

徐 勇，王伟娜，周莹莹，苏金乐

(1.河南农业大学林学院，河南 郑州 450002; 2.中共中央党校研究生院，北京 100091;3.河南中医药大学，河南 郑州 450008)

基于空间连通度的江南园林庭院空间研究

徐 勇1，王伟娜2，周莹莹3，苏金乐1

(1.河南农业大学林学院，河南 郑州 450002; 2.中共中央党校研究生院，北京 100091;3.河南中医药大学，河南 郑州 450008)

以何园“片石山房”和艺圃“响月廊”2个景观节点为例，结合几何和数学的方法，基于空间连通度对2个庭院空间进行量化分析，发现主要节点的空间平均连通度均趋近于黄金比例0.618。以此为切入点，构建出一个空间平均连通度为0.618的空间模型—凹型模，在符合中国园林传统美学基础上使园林庭院空间及建筑空间的数字化设计成为可能。

空间连通度；量化分析；黄金比例

“步移景异”是江南园林空间营造的一个重要手法，它是指在园林空间内，随着观测者位置的移动，所观测到的景观也随之发生改变。这里的“移”和“异”都是一种变化，是由空间的“移”带来景观上的“异”，这种变化在江南园林庭院空间中也得到了充分体现[1]。很多研究都是通过图片、插图或者文学化的描述从“移”和“异”的结果来阐释“步移景异”，而“步移景异”表象下各个空间和景观要素之间的绝对位置其实是没有发生变化的，这些空间和景观要素之间存在一定的关联性和逻辑性。本研究尝试弥补传统的仅从园林表象上“移”和“异”——即仅从空间观测者角度考虑，而是兼顾空间、景观要素的客观绝对位置和观测者主观感受两方面出发——既能实现空间研究的可操作性，便于形成直观有效的设计方法，又能尊重江南园林庭院空间的流动性和观测者的能动性，运用数学方法研究江南园林“步移景异”表象背后的内在联系[2]。利用空间连通度对江南园林庭院的空间序列进行量化研究，将其数据化并进行定量分析和美学比较，为园林庭院的空间设计提供数字化支持。

1 概念与方法

空间连通度的概念是基于匀质空间和园林美学两个不同研究领域而发展来的，多适用于园林庭院空间[3-4]。

“匀质空间”理论最早是由密斯·凡德罗提出的，他是将“匀质空间”运用到建筑实例中的践行者。匀质空间的主要特征是：各空间要素处于同等地位，具有各向同性，空间的轴线性减弱，没有主要空间和次要空间，以匀质的理念处理建筑的每一寸空间，空间本身就是一个产生较小的偏差和动感的匀质场，使建筑外部具有完整轮廓[5]。

关于园林美学的研究，金学智[6]首先在《中国园林美学》中提出了“中国园林美学”的概念，他认为中国园林在生态意识的启发下将“走向新的私家院落、庭院”；宗白华[7]从“建筑空间”的角度来看待中国园林的艺术性，将中国园林称之为“建筑空间艺术”，他认为“建筑和园林的艺术处理，是处理空间的艺术”；汉德宝[8]在美学的基础上，认为中国园林从西方功能主义的角度来判断，园林建筑满足了美的需要，是具有美学功能的建筑。

1.1概念

空间连通度(COS，C)：连通体积与母空间的总体积之商[9]。

所以在同一水平面内，当2个围合空间A和B通过连通媒介S相连通，2个空间的空间连通度0≤C≤ 1。

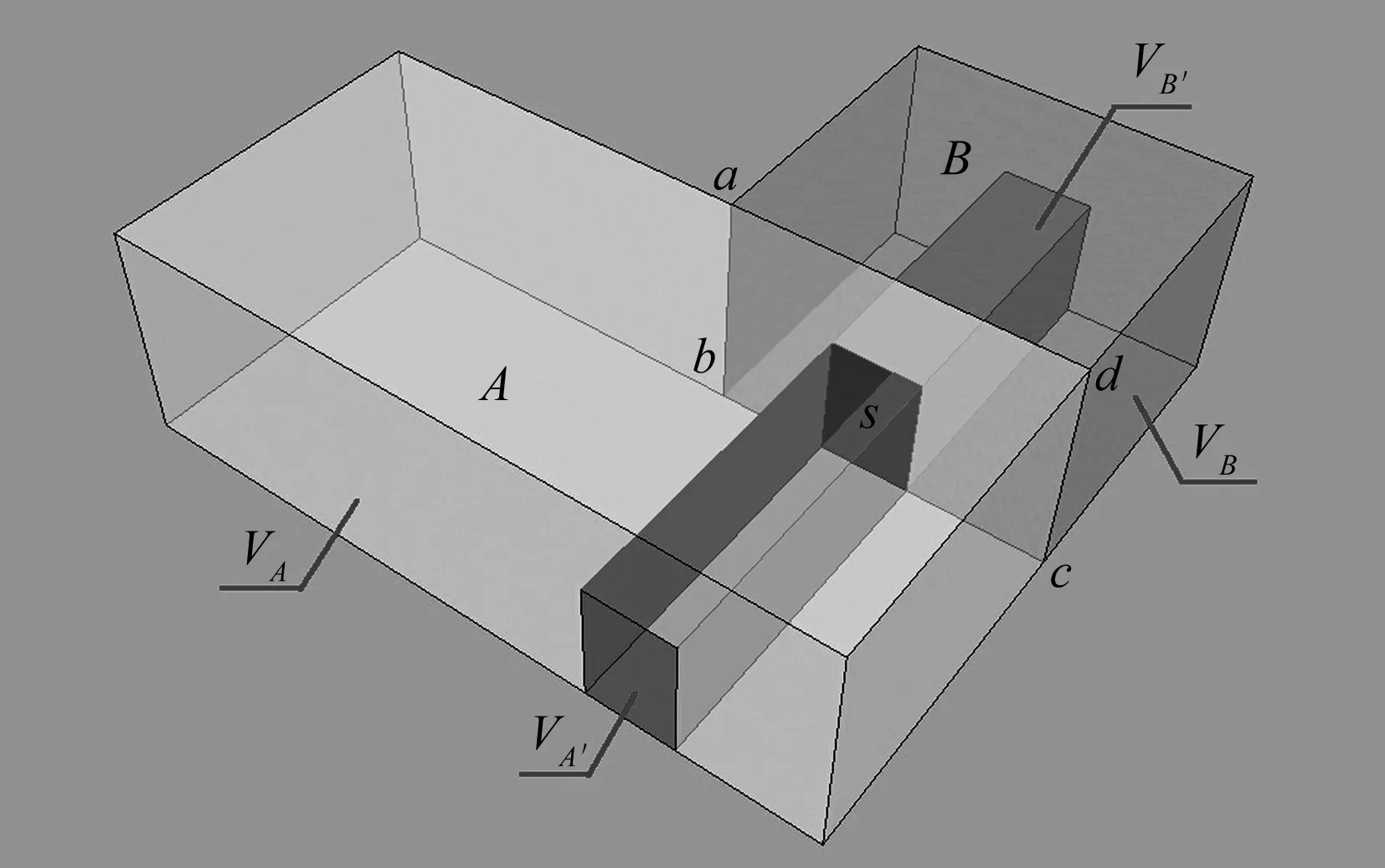
图1 空间连通度示意图aFig.1 COS a

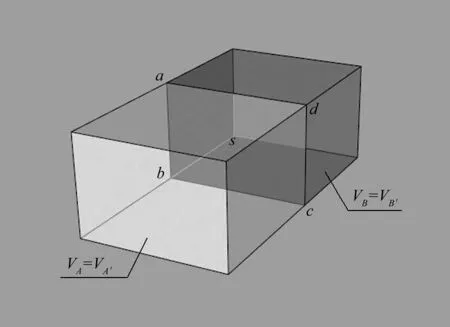
图2 空间连通度示意图bFig.2 COS b

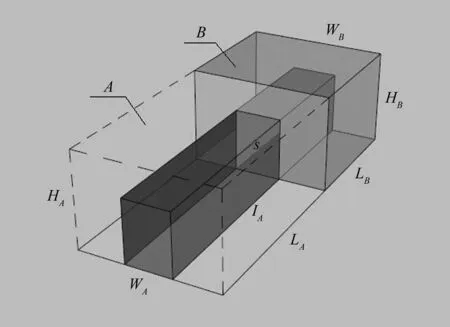
图3 空间连通度示意图cFig.3 COS c

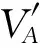
所以在同一水平面内，当围合空间B与开敞空间A通过连通媒介S相连通，两个空间的空间连通度0≤C≤ 1。

空间平均连通度C均：在水平空间内，中心空间V1与周围相邻空间(V2、V3、V4、V5)的空间连通度均值，即为V1空间的空间平均连通度C均(图4、图5)。

因为0≤C≤ 1，所以0≤C均≤ 1。

图4 主空间与相邻空间连通示意图Fig.4 The diagram of central space and its connecting spaces around

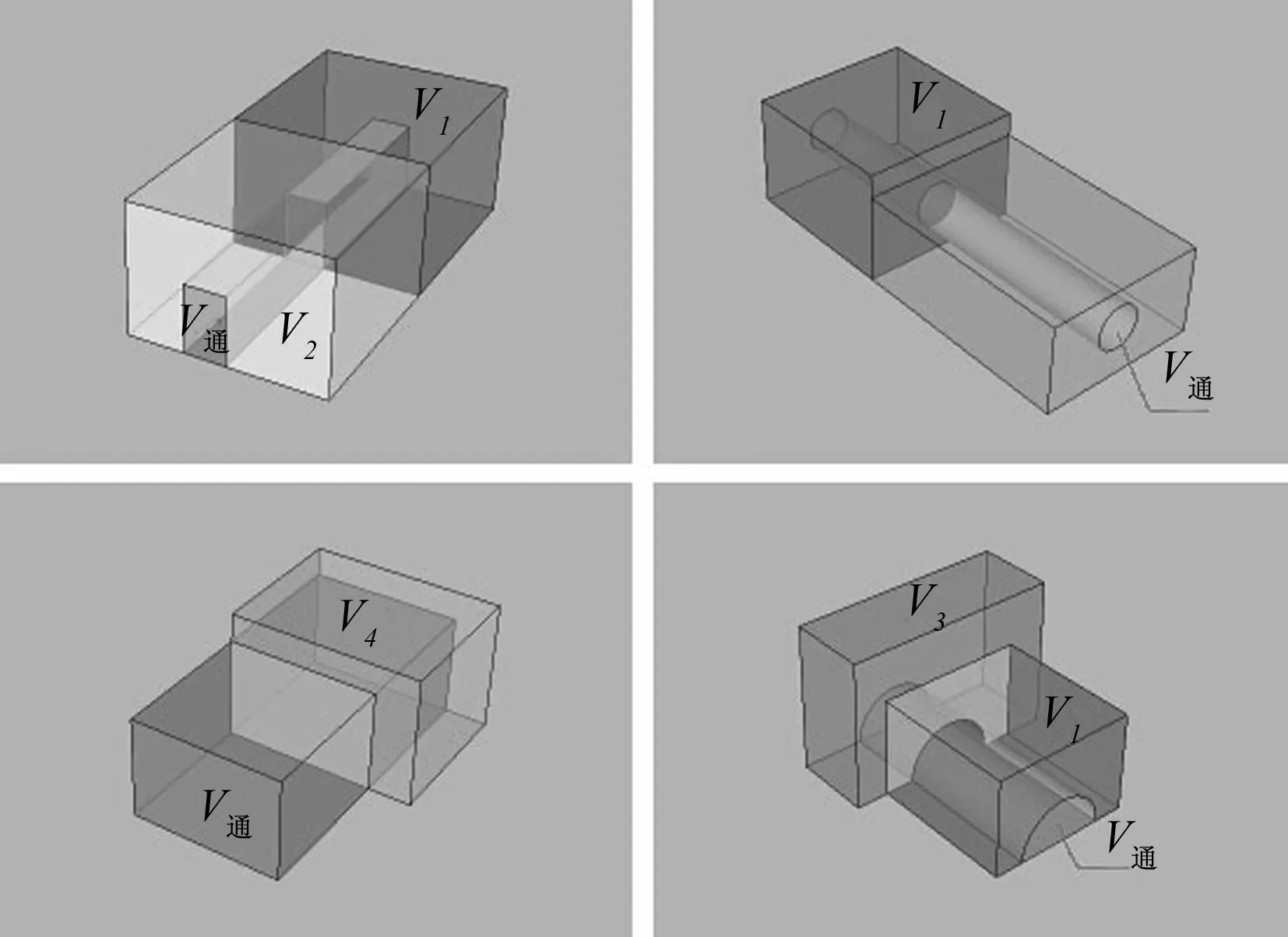
图5 主空间与各空间连通示意图Fig.5 The diagram of central space and other spaces around

1.2方法

以空间连通度为基础，对中国江南园林庭院的景观节点空间进行量化分析，分别以片石山房的“琴棋书画厅”和艺圃的“响月廊”两个重要景观节点为例。首先对两个景观节点的空间进行划分，然后计算得出各空间的空间连通度C以及空间平均连通度C均，通过分析比较各C均值，归纳出空间与景观要素之间的内在关联性和逻辑性。

2 研究过程与结果

2.1片石山房现状分析

片石山房相传是清代大画家石涛和尚的叠石孤本，坐落在扬州何园一隅，自成一院。院内假山、流水、建筑相映成趣，尤以“琴棋书画厅”最易引起游客驻足，品室内之意，赏室外之景，乃院内最佳观景点(图6)。下面将以“琴棋书画厅”及厅前水榭为例，对其进行空间连通度分析。

图6 片石山房鸟瞰图Fig.6 The aerial view of Pianshishanfang

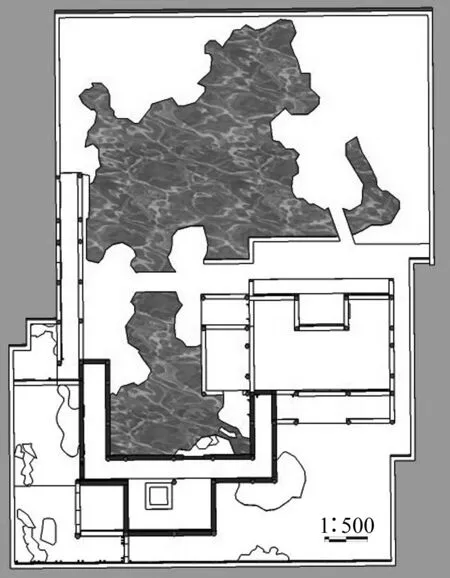
图7 “琴棋书画厅及长廊”计算范围示意图Fig.7 The calculation range diagram of Qinqishuhua Hall and the gallery

2.1.2 “琴棋书画厅”及厅前水榭空间连通度的计算分析 为方便计算，将“琴棋书画厅”及厅前水榭空间划分4个独立的空间，分别是(V1)空间、(V2+V3+V5)空间、(V4)空间和(V6)空间(图9)。V2是(V1)空间与(V2+V3+V5)空间相连通的位于(V2+V3+V5)空间的部分，(V1)空间和(V2+V3+V5)空间的连通总空间为(V1+V2)；V5是(V6)空间与(V2+V3+V5)空间相连通的位于(V2+V3+V5)空间的部分，(V6)空间和(V2+V3+V5)空间的连通总空间为(V5+V6)；(V2+V3+V5)空间与(V4)空间因为有高差，所以两个空间相连通的位于(V2+V3+V5)空间的部分不再单独标注，而在计算过程中直接写出(图4、图5)。

图8 “琴棋书画厅及长廊”空间划分示意图Fig.8 The space division diagram of Qinqishuhua Hall and the gallery

图9 “琴棋书画厅及长廊”空间连通示意图 Fig.9 The cos diagram of Qinqishuhua Hall and the gallery

图10 “琴棋书画厅及长廊”空间计算示意图Fig.10 The space calculation diagram of Qinqishuhua Hall and the gallery

C1：(V2+V3+V5)空间和V1空间的空间连通度，C1≈0.406

C2：(V2+V3+V5)空间和V4空间的空间连通度，C2≈0.733

C3：(V2+V3+V5)空间和V6空间的空间连通度，C3≈0.315

C4：(V2+V3+V5)空间和开敞水面的空间连通度，C4≈1

C均：(V2+V3+V5)空间的空间平均连通度，C均≈0.614

2.2艺圃现状分析

艺圃全园分住宅、花园两部分，宅分5进，园在宅西，水池居中。池北以建筑为主，池南以山景为主，延光阁、响月廊、乳鱼亭抱水而立，体量由大变小，是园内的主要观景点。响月廊滨水而倚，由北向南行。既可漫步赏景，又可驻足休憩。以响月廊为例，对其空间连通度进行分析计算。

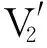
2.2.2 响月廊空间连通度的计算分析 左侧空间(V1)、中心空间(V2+V3+V4))、右侧空间(V5)分别是3个独立空间。观测者易在中心空间内驻足休憩，所以将中心空间设为主体空间。为方便计算，将中心空间划分为V2、V3、V43个小空间。中心空间与左侧空间的空间连通体积为(V1+V3)，中心空间与右侧空间的空间连通体积为(V3+V4+V5)(图12)。

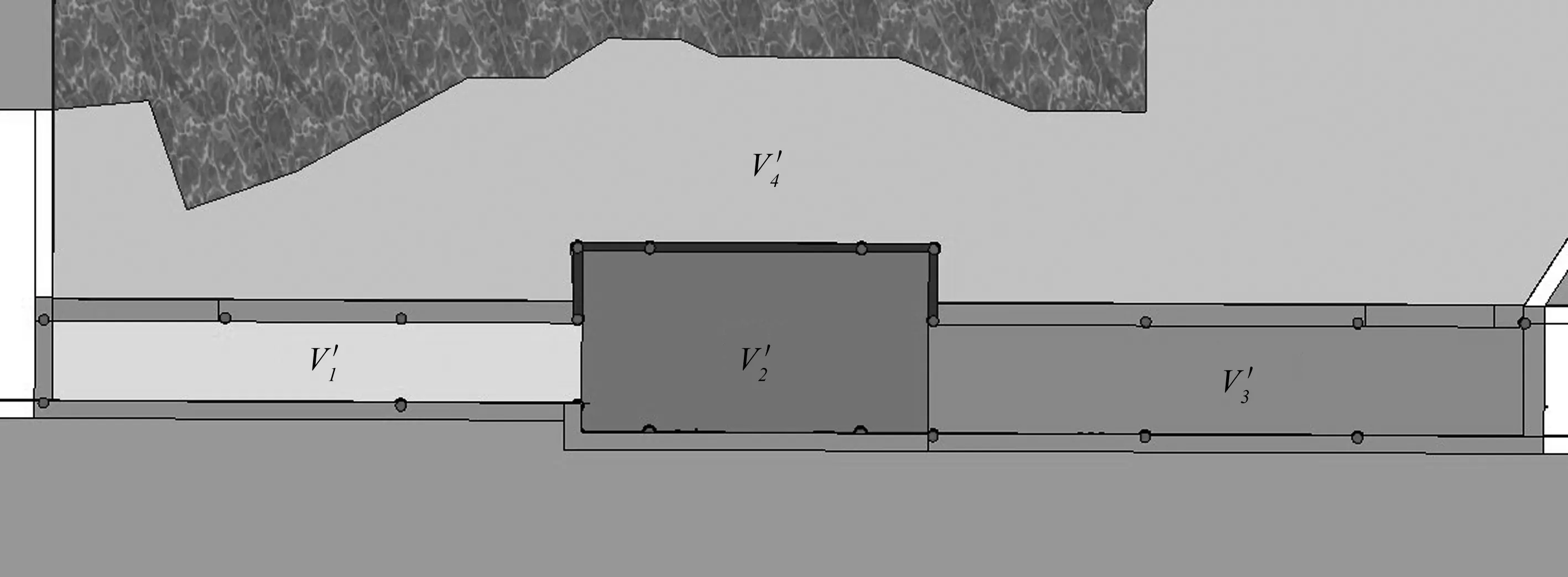
图11 响月廊空间划分示意图 Fig.11 The space division diagram of Xiangyue Gallery

图12 响月廊空间连通示意图Fig.12 The space division diagram of Xiangyue Gallery

中心空间是驻足休憩空间，此观景点廊壁上有一矩形窗与外界相连通(图13)。此窗以窗界为框，以窗外的竹子为图，以白墙为底，窗与窗外之景构成了一幅随四季更替而变化的画卷。其功能更多是以画卷为表现形式，故此窗在本次计算中忽略不计，中心空间在该方向的C值为0。

图13 透窗示意图Fig.13 The diagram of through the window

图14 响月廊空间计算示意图Fig.14 The space calculation diagram of Xiangyue Gallery

C1：中心空间和左侧空间的空间连通度，C1≈0.661

C2：中心空间和右侧空间的空间连通度，C2≈0.802

C3：如图13所示，C3=0

C4：中心空间和水面的空间连通度，C4≈1

C均：中心空间的空间平均连通度，C均≈0.616

3 结论与建模

3.1结论

片石山房“琴棋书画厅”及长廊、艺圃的响月廊2个庭院空间的空间平均连通度C均的值分别为0.614、0.616，都接近黄金比例0.618。这种现象的出现不是偶然的，而是一种客观存在，类似园林庭院空间结构的空间平均连通度与黄金比例0.618之间有着必然的内在联系[10]。

以上2个例子在空间类型上，都是中国江南园林庭院空间里的主要节点，功能皆以赏景为主；它们的体量不大，均以精致小巧见长；它们的主要连通空间一侧都紧邻开敞空间，两侧与小空间相连通，整体空间呈“凹”型分布。

综上所述可以得出以下结论：江南园林庭院空间的设计在主观上满足观测者“步移景异”这种视觉变化的同时，客观上的园林构筑物空间及景观要素之间的绝对位置是保持不变的。这种不变是以空间连通度COS的形式，以0.618为“锚点”上下浮动而存在。庭院空间的景观设计评判除了以给人视觉的舒适或者感觉上的愉悦等主观的抽象的概念为标准之外，也可以以几何学的空间平均连通度C均值为0.618为准则，在尊重江南园林空间流动性和观测者能动性的基础上，运用几何学方法对园林庭院空间进行数字化设计。这种量化的数学逻辑之美与中国江南古典园林所追求“虽由人作，宛自天开”的自然美殊途同归，有着异曲同工之妙，在江南园林庭院空间中得到了充分体现。

3.2建模

根据以上结论构建出一个以空间连通度为基础的“凹”型园林庭院空间模型：

在“凹”型空间模型里(图15)，V1～V5空间不仅是建筑空间，也可以是由园林植物构成的围合空间或者其他空间。其中V2是主体空间，与V1、V3、V4、V54个空间相连通；V5空间是开敞空间，可为水面、草坪等，V2与V5的空间连通度C≈1。

当V2的空间体积不变时，(V1+V4)的空间体积与V3的空间体积成反比例，当(V1+V4)的空间体积变大，则V3的空间体积变小；V3的空间体积的最小值为0，即该方向不连通，V2与V3的空间连通度C≥0；当(V1+V4)的空间体积变小，则V3的空间体积变大。按此规则，V1、V2、V3、V44个空间的空间整体体积处于一种平衡状态，这种平衡以V2的空间平均连通度C均=0.618为“锚点”上下浮动。当V2的空间平均连通度C均值接近0.618时，观测者处于V2空间内就会获得较舒适的观感，以此模型为基础设计的景观节点适于规划在景区较好的景观位置；当V2的空间平均连通度C均值远离0.618时，观察者在V2空间内的观赏到的景观效果就会削弱，由此设计的景观节点应设置在景区的次要景观位置。

图15 “凹”型模示意图Fig.15 The diagram of the “concave” model

江南园林庭院空间的空间平均连通度C均=0.618的发现以及“凹形模”的构建，是从江南古典园林中走出的现代数学之美。以此模型为基础设计的庭院空间，符合中国古典园林传统美的同时，还具备数学美感，符合几何学的比例性和逻辑性规律[11]。隐藏在“步移景异”表象背后的空间平均连通度0.618，与“移”和“异”有着异曲同工之妙，给观测者带来视觉上的舒适和情感上的愉悦，使庭院空间的数字化设计成为可能。

[1] 李帅波,周莹莹,田国行.被掩盖的理性—留园石林小院院落空间解读[J].华中建筑,2011,38(1):169-173.

[2] 原口秀昭.空间构成的比较分析[M].谭纵波,译.北京:中国建筑工业出版社,1997.

[3] 余树勋.园林美与园林艺术[M]. 北京:科学出版社,1987.

[4] 李泽厚.美的历程[M]. 北京:文物出版社,1989.

[5] 原口秀昭.世界20世纪经典住宅设计[M].谭纵波,译.北京:中国建筑工业出版社,1997.

[6] 金学智.中国园林美学[M]. 南京:江苏文艺出版社,1990.

[7] 宗白华.中国园林艺术概观[M]. 南京:江苏人民出版社,1987.

[8] 汉宝德.物象与心境:中国的园林[M].北京:生活·读书·新知三联书店,2014.

[9] 金伯利·伊拉姆.设计几何学:关于比例和构成的研究[M].李乐山,译.北京:中国水利水电出版社,2003.

[10] 丹·艾瑞里.怪诞行为学[M]. 赵德亮,夏蓓洁,译.北京:中信出版社,2010.

[11] 亚历山大·佐尼斯.机器与隐喻的诗学[M].金秋野,王又佳,译.北京:中国建筑工业出版社,2004.

(责任编辑：李 莹)

ResearchoncourtyardspaceofChinesesoutherngardensbasedontheconnectivityofspaces

XU Yong1，WANG Weina2，ZHOU Yingying3，SU Jinle1

(1.College of Forestry， Henan Agriculture University，Zhengzhou 450002，China; 2.Graduate School of CCPS，Beijing 100091，China; 3.Henan University of Chinese Medicine，Zhengzhou 450002，China)

This article, using geometric and mathematical methods, quantizes the space on courtyard-space of Chinese southern classical gardens-taking the “Pian Shi Shan Fang” of He yuan Garden and the “Xiang Yue Lang” of Yi Pu as examples-based on the connectivity of spaces. The author found that the average spatial connectivity of the important landscape nodes are close to the gold ratio of 0.618. Taking this as the breakthrough point, a space model called “concave mold” is constructed, whose average connectivity of spaces are 0.618. This makes the digital design of courtyard space and architectural space possible.

connectivity of spaces(COS)；quantitative analysis； golden ratio

TU 986.2

：A

2016-07-30

河南省社科类基金项目(SKPJ201414)

徐 勇(1984-)，男，河南许昌人，博士研究生，主要从事风景园林规划与设计的研究。

苏金乐(1953-)，男，河南新郑人，教授,博士研究生导师。

1000-2340(2017)02-0195-06