运动目标跟踪的粒子滤波算法

于 勇，车燕芳

(中国船舶重工集团公司第七二三研究所, 江苏 扬州 225001)

运动目标跟踪的粒子滤波算法

于 勇，车燕芳

(中国船舶重工集团公司第七二三研究所, 江苏 扬州 225001)

提出一种基于对数极坐标变换的改进粒子滤波算法，以解决传统粒子滤波算法中由于红外成像目标信息量少所导致的目标跟踪稳定性低、易于发散的问题。该算法在粒子滤波的理论框架下，利用跟踪区域的对数极坐标变换作为目标描述，建立了一种稳健的系统观测模型，有效突出了目标信息，减弱了目标的旋转和尺度变化对跟踪算法的影响。该算法结合了粒子滤波运动估计的鲁棒性以及对数极坐标变换目标描述的稳健性，可在复杂环境中实现对目标的稳定跟踪。

运动目标跟踪；粒子滤波；对数极坐标变换；灰度直方图

0 引 言

运动目标跟踪是红外成像目标探测的关键技术。由于红外成像目标的信息量少、运动不规律、机动性强，易产生的遮挡与淹没效应等，使得目标跟踪算法较为复杂。传统的红外目标跟踪采用模板匹配的方法[1]，跟踪过程中目标姿态以及尺度的变化会对该方法的匹配精度产生较大影响。

基于统计学的目标跟踪算法以马尔可夫随机场为基础对图像进行建模与优化估计，主要包括Mean Shift算法、卡尔曼滤波以及粒子滤波算法等。粒子滤波的基本思想是采用带有权重的粒子集来表示系统的状态估计，并通过序贯重要性采样更新粒子集，实现系统状态的动态估计[2]。相对卡尔曼滤波以及Mean Shift算法，粒子滤波提供了一种非线性非高斯系统状态估计的方法。系统观测模型是影响粒子滤波算法跟踪性能的关键问题，常用的方法中采用颜色分布作为目标的描述来建立系统观测模型[3]，由于红外图像的信噪比低、目标信息量不足且灰度级数少，仅仅依靠灰度分布很难准确区分目标与背景，在场景复杂或目标高速运动时跟踪可能会不稳定甚至完全失败。

图像对数极坐标变换(LPT)[4]提供了一种具有旋转和尺度不变性的目标匹配方法，但该方法在处理笛卡尔坐标系下较为简单的平移变换时，需要对图像进行逐点匹配，从而降低了目标跟踪的效率。从粒子滤波对目标运动估计的鲁棒性以及对数极坐标变换对目标描述的稳健性出发，本文提出了一种基于对数极坐标变换的改进粒子滤波算法，其核心思想是将粒子采样位置作为对数极坐标变换的中心，利用样本区域与参考模板对数极坐标变换后的图像相关性计算粒子权值，从而得到目标跟踪位置。对数极坐标变换的旋转和尺度不变性提高了系统观测概率模型的区分性和稳定性。相对于传统的利用灰度分布描述红外目标的粒子滤波算法，本文算法的跟踪鲁棒性与稳定性有较大提高。

1 粒子滤波

离散系统的状态方程和测量方程可表示为：

(1)

式中：xk为k时刻的状态向量；yk为k时刻的观测向量；fk为状态转移函数；hk为观测函数；wk为零均值噪声；vk为测量噪声。

则xk在最小方差意义下的最优估计可由下式的条件均值给出：

(2)

根据Bayes准则，p(xk|y1:k)的递推过程由预测与更新2步组成。已知k-1时刻的概率密度p(xk-1|y1:k-1)，k时刻的先验密度可根据Chapman-Kolmogorov方程预测为：

(3)

在得到时刻k的测量值yk之后，可利用Bayes准则对预测值进行更新，即求取下式的后验概率密度：

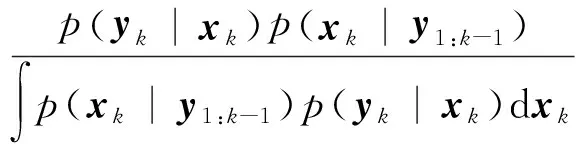
(4)

这样，式(3)与式(4)的组合就构成了贝叶斯估计预测与更新的过程。

粒子滤波是利用状态空间的一组带权值的随机样本粒子来逼近后验概率的方法。根据蒙特卡罗理论，当粒子的数目足够多时，这组具有权值的粒子就能完全地描述后验概率分布，此时粒子滤波就是最优的贝叶斯估计。

π(x0:k|y1:k)=π(xk|x0:k-1,y1:k)π(x0:k-1|y1:k-1)

(5)

如果π(xk|x0:k-1,y1:k)=π(xk|x0:k-1,yk)，即重要性分布函数仅与当前观测值yk和前一个状态xk-1相关，则可得到权值的更新为:

(6)

则k时刻的后验概率密度可利用冲激函数δ近似为:

(7)

2 基于对数极坐标变换的目标观测模型

目标描述的区分性和稳定性是影响跟踪算法稳健性的关键。描述目标的常用特征有颜色分布以及轮廓曲线等。然而，红外目标一般都没有鲜明、稳定的轮廓，同时红外目标灰度级数少，复杂场景下灰度分布与背景差异不明显，因此采用灰度分布作为目标描述也是不可靠的。

本文采用目标区域对数极坐标变换后的图像作为目标的描述，通过计算对数极坐标变换后的目标样本与参考目标图像的相似性度量，建立系统观测概率模型。该方法具有以下优点：首先，对数极坐标变换后图像的中心分辨率较高且沿径向呈指数递减，充分突出了处于区域中心的目标信息，克服了红外目标信息量低的缺点；其次，笛卡尔坐标系下目标图像的尺度和旋转变换经对数极坐标变换后转变为沿对数极坐标系的平移运动，具有较好的尺度和旋转不变性。

2.1 红外目标的对数极坐标描述

对数极坐标变换来源于对人眼空间变分辨率机制的研究，它表达了一种图像描述的变化。对于选定区域的坐标原点O(0,0)，假设均匀取样的图像空间(笛卡尔坐标系)像素点的坐标为(x,y)，可将其用复数表示为z=x+iy，对z进行对数映射可得:

w=ln(z)=ξ+jφ

(8)

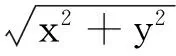
(9)

(10)

式中：(r,θ)为(x,y)对应的极坐标点。

从上式可以看出，z空间(笛卡尔坐标系)中的像素点(x,y)映射成w空间(对数极坐标系)中的坐标点(ξ,φ)。

接下来分析对数极坐标的尺度和旋转不变性，假设z空间目标相对于坐标原点的尺度变化因子为r0，旋转角度为θ0，则经过尺度和旋转变化后的对数极坐标映射为w=lnz=lnr0r+i(θ0+θ+2π)，即：

ξ=ln(r0r)=lnr0+lnr

(11)

φ=θ0+θ+2kπ

(12)

显然，笛卡尔坐标系中目标尺度与旋转变化，映射到对数极坐标变换阵中，目标区域的形状未发生变化，尺度与旋转变化仅仅表现为目标区域沿极径(ξ)以及极角(θ)方向的平移，而这种平移可以通过归一化的方法较容易地处理。

图1为不同尺度与姿态下红外图像以及相应的对数极坐标变换，由图1可见同一目标的对数极坐标描述不因目标大小以及飞行姿态的变化而变化，且离中心越远的像素分辨率越低，突出了模板中心的飞机目标信息，提高了目标描述的可靠性。本文的目标LPT模板中图像分布比较均匀，有多个波峰与波谷存在，这种依靠形状信息的目标描述方法所包含的信息较为丰富，使得目标相对于背景以及干扰的区分性更强，在干扰状态下的跟踪也更为稳健。

2.2 目标观测模型

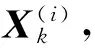
(13)

(14)

因此，观测概率模型可定义为：

(15)

由上式可见，相似性度量越小，样本的权值越大，样本越可靠。

3 运动目标跟踪的改进粒子滤波算法

粒子滤波通过状态空间中1组随机的自适应演化粒子去探索状态空间的发展变化，每个粒子代表1个可能的目标状态变化轨迹。在运动目标跟踪中，可以将状态向量表示为Xk=[cx,cy,vx,vy]T，其中(cx,cy)是目标中心位置，(vx,vy)表示目标的运动速度。与传统的跟踪算法不同，粒子滤波随机模拟的特性使得算法的稳健性不会过度依赖于状态转移模型。因此，本文采用线性模型作为系统状态转移模型的近似描述：

Xk-Xk-1=Xk-1-Xk-2+uk

(16)

式中:uk为零均值高斯随机过程。

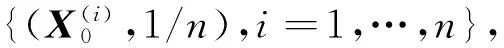
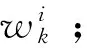
4 实验分析

采用1组含干扰的飞机目标图像序列进行运动目标跟踪，并将跟踪结果与传统的粒子滤波跟踪结果进行比较，以考察本文算法在干扰环境下的跟踪鲁棒性。图2(a)为采用灰度直方图作为目标特征描述的传统粒子滤波跟踪结果，从图中可以看出，飞机抛洒出的诱饵与目标的灰度基本一致，使得该方法中一旦出现诱饵，很容易使得跟踪偏离目标区域，导致最终的跟踪失败。

图2(b)为采用本文算法的目标跟踪结果。可以看出，在目标被部分遮挡时，本文方法仍能够准确跟踪目标，而当目标被短暂遮挡时，粒子的权值非常小(LPT相关系数低)，因此跟踪的准确性主要依赖于状态转移模型。在较短的时间间隔内，本文状态转移模型所采用的二阶自回归方程可以近似认为与目标的运动是一致的。因此，在遮挡状态下跟踪点并未产生大的偏移。当目标脱离诱饵时，算法能够再次捕获目标。从上述分析可见，本章算法在短暂遮挡状态下跟踪性能受影响较小，鲁棒性超过了传统的粒子滤波算法。

5 结束语

本文提出了一种基于对数极坐标变换的改进粒子滤波算法。利用跟踪区域的对数极坐标变换作为目标描述，建立了一种稳健的系统观测模型，有效突出了目标信息，减弱目标的旋转和尺度变化对跟踪算法的影响，使得算法更加适合于处理信息量少、机动性强的红外目标跟踪问题。实验结果表明，相对于传统的粒子滤波算法，本文算法的跟踪鲁棒性与稳定性有较大提高，可实现复杂环境下的红外目标跟踪。

[1] 杨皞昀,张桂林.一种新的相关跟踪算法的设计与实现[J].红外与毫米波学报,2000,19(5):377-380.

[2] GORDON N,SALMOND D,SMITH A.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].IEE Proceedomgs.F，1993(140)：107-113.

[3] NUMMIARO K,KOLLER M E,GOOL L.An adaptive color-based particle filter[J].Image and Vision Computing,2003，21(1)：99-110.

[4] 许东,安锦文.基于图像对数极坐标变换的多分辨率相关匹配算法.西北工业大学学报,2004,22(5):653-656

[5] RISTIC B,ARULAMPALAM S,GORDON N.Beyond The Kalman Filter:Particle Filters for Tracking Applications[M].Boston,USA:Aretech House,2004.

[6] DOUCET A，FREITAS N，GORDON N.Sequential Monte Carlo Methods in Practice[M].New York,USA：Springer-verlag，2001.

[7] DOUCET A，GODSILL A，ANDRIEU C.On sequential Monte Carlo sampling methods for Bayesian filtering[J].Statistics and Computing，2000,10(3)：197-208．

[8] NUMMIARO L,KOLLER-MEIER E,VAN GOOL L.An adaptive color-based particle filter[J].Image Vision Comput.,2003，21(1):99-110.

[9] 于勇,郭雷.基于粒子滤波的红外运动目标跟踪[J].计算机应用,2008,28(6):1543-1545.

[10] MASKE S,GORDON N.A tutorial on particle filters for nonlinear/non-gaussian bayesian tracking[C]//Proceedings of IEEE Workshop,Target Tracking：Algorithms and Applications，2001.

ParticleFilteringAlgorithmforMovingTargetTracking

YU Yong,CHE Yan-fang

(The 723 Institute of CSIC,Yangzhou 225001,China)

An improved particle filtering algorithm based on log-polar transform (LPT) is presented,which can solve the problems that target tracking stability is low and easy to be diverged due to little infrared imaging target information in the traditional particle filtering algorithms.Based on the theory of particle filtering,the algorithm uses the LPT of tracking area as target description,sets up a stable system observation model,which effectively highlights the target information,weakens the influence of target rotation and scale transformation on tracking algorithm.The algorithm combines the robustness of particle filtering movement estimation and the solidity of LPT target description,which can realize the stable tracking to target in complex environment.

moving target tracking;particle filtering;log-polar transform;grey level histogram

TP391

：A

：CN32-1413(2017)04-0046-04

10.16426/j.cnki.jcdzdk.2017.04.012

2017-06-22