一种基于帧间差分与模板匹配的河水表面流速测量方法
2017-09-23赵晓刚王书志
赵晓刚 冯 全* 王书志
1(甘肃农业大学工学院 甘肃 兰州 730070)2(西北民族大学电气工程学院 甘肃 兰州 730030)
一种基于帧间差分与模板匹配的河水表面流速测量方法
赵晓刚1冯 全1*王书志2
1(甘肃农业大学工学院 甘肃 兰州 730070)2(西北民族大学电气工程学院 甘肃 兰州 730030)
为了解决常见几种流速测量方法受含沙量与漂浮物影响大、设备与人力成本高的局限性,提出一种基于机器视觉的河水表面流速测量方法。我们分析了图像空间与现实空间的位置映射关系,得出了物理速度与图像速度之间的关系。通过垂直于水面的摄像头获取河流视频,采用帧差处理获得帧差图像,检测出其中运动显著性比较明显的一些区域作为模板。最后,基于模板匹配的方法检测出模板的像素位移,联立图像坐标系和与现实空间坐标系的位置映射关系以及帧间时间计算出河流表面实际流速。实验结果表明,该测速方法对自然条件下流速相对平缓的河流视频具有较好的效果,误差小于3%,可持续监测水流流速情况。
流速测量 模板匹配 视频处理 帧差法
0 引 言
我国的河流众多,水文监测信息对预防治理洪涝和水旱灾害以及水资源调控具有重要作用。而流速测量是水文监测的重要工作之一,但是目前的流速测量方法用方面都有一定的局限性。常用的河水流速测量方法主要分为三类。第一类是传统的流速仪测量法[1],其主要原理是通过水流带动旋桨转动,记录旋桨转速,通过一定的映射关系可算出流速,但存在着当水质突变,含沙量变大时误差会变大,且水中漂浮物会影响其结果甚至损毁旋浆的问题。第二类是通过声学多普勒效应来测量流速[1],主要用于测量船,也存在着设备和人类投入比较大、成本比较高的问题。第三类是浮标法,其中比较先进的是基于视频处理与浮标法相结合的水流速度测量方法,例如韩予皖[1]通过跟踪水流视频中浮标的运动轨迹结合摄像机标定来计算水流速度,但该方法需要投掷浮标,无法实现对水流速度的不间断实时监控。针对以上问题,本文试图探索一种不受含沙量与漂浮物影响,设备和人力成本低且可持续实时监控的水流流速测量方法。
传统模拟摄像机原本分辨率就不高,加之要受到反复的A/D转换、电磁传输干扰、D1画面的合成反交错等视频损伤,使得图像细节纹理丢失严重。流水运动产生的细节在视频上往往观察不清,因此传统的方法需要投掷浮标或者抛洒示踪粒子,通过观察浮标的运动才能在图像中分析流水的运动。随着科技的发展与技术的进步,数百万乃至千万分辨率的高清摄像机应用越来越广泛。借助高清摄像机能很好地观测到水面波动的纹理细节。本文在利用高清摄像头拍摄序列图像(视频)的基础上,提出了一种河水表面流速测量方法。该方法分析河水流动过程中本身产生的波动纹理特征或自然漂浮物来检查具有显著运动的区域,以这些区域为模板,在随后的视频图像中搜索匹配区域,以此估计这些区域的运动位移,结合摄像机标定来计算水流速度。具体来说是采用帧差法[2-6]计算出帧差图像,在t时刻帧差图像提取出其中具有显著运动的小目标作为模板,在t+△t时刻帧差图像中,用模板匹配[7-11]法找到与之对应的最佳匹配坐标,从而计算出各模板的相对位移,求出所有模板的平均相对位移后,最终结合摄像机标定结果计算水流流动速度,流程如图1所示。本方法的优点是不需要投掷浮标,可连续测量,人力和设备成本低。

图1 系统流程图
1 摄像机标定
基于机器视觉的速度测量方法需要通过摄像机标定来建立二维图像尺度与世界三维空间坐标系中的真实尺度之间的映射关系。如果将摄像机固定在水面正上方,并将摄像头光轴垂直指向水面,则水流流动可看做是一种二维运动,流速计算可简化为二维运动估计问题[12-14],摄像机标定模型为一种线性模型,即透视投影成像模型[1]。
根据透视投影成像模型,二维图像尺度与世界三维空间坐标系中的真实尺度之间存在线性关系。应用到本文中,水面上存在的B、C两点其在二维图像上的映射为B’、C’,则B、C的距离dbc与B’、C’的距离db′c′(像素意义)有如下数学关系:
dbc=k·db′c′
(1)
由于水流都是在河道中流动,实验时只需要计算流速,而不必考虑其方向。当光照可靠时,物距固定且摄像头焦距固定的情况下,其成像大小总是一致的。所以放大倍数k是一定的。摄像机标定主要工作就是获取k,通过实验可获得k值,从而建立像平面速度与实际速度之间的关系。
2 流水视频处理与表面流速测量
2.1 模板提取
当视频中有物体运动时,帧与帧之间会有明显的差异,两帧相减得到两帧差的绝对值作为帧差图像,可以在帧差图像上分析物体的运动特性。在自然条件下,河流流动时,受到重力和表面张力的影响,总是不平静的,会天然地产生波动。一帧图像上波动可能很弱,但从帧差图像上却容易判断水流的波动,这为本文通过视频处理来获取水流速度提供了可靠的目标。
假设很短的时间内小目标的运动状态基本不变,本文通过检测跟踪这些天然目标最终得出水流流动速度。而为了捕捉这些细小的波动,本文计算了帧差图像:
ΔI(u,v,t1)=|I(u,v,t1)-I(u,v,t2)|
(2)
其中:I(u,v,t1)是视频在t1时刻那一帧在点(u,v)处的灰度值,ΔI(u,v)是t1时刻与t2时刻灰度图像差的绝对值。本文需要统计连续多帧上的小目标速度,采用连续帧差的检测方案(通常取连续三帧,分别是t-Δt、t和t+Δt,Δt为相邻两帧的间隔时间),即让t-Δt时刻的灰度图像与t时刻的灰度图像做帧差,表示为Ct-;再让t时刻的灰度图像与t+Δt时刻的灰度图像做帧差,表示为Ct+。然后将Ct-进行二值化处理,其数学表达为:
(3)
其中:T为设定的阈值函数。
因为同一视频每一帧的灰度存在差异,设定固定的阈值会造成某些帧无法检测到目标或者目标数量太少,所以本文采用动态阈值,会自动根据灰度最大值调整系统阈值,即:
T=α·max(ΔI(u,v,t))
(4)
其中:α为常数因子,实验中取0.95。
帧差图像经过二值化后被分割为多个连通域,将各个连通域用最小矩形包围,本文将二值图C2t-中各矩形区域做为掩模,将它们在Ct-中对应的矩形区域设定为模板。考虑到本文后续处理采用的是模板匹配的方式来计算河流速度,模板面积太大则运算量大,耗费时间,模板面积太小则匹配精准度不高,故应选取模板面积大小合适的连通域作为检测目标,如此则选取合适的掩模PS,其面积属于区间[S1,S2]。一个模板可表示为:
bboxPs=(u,v,w,h)
(5)
其中:(u,v)为模板左上角坐标,w与h分别矩形的宽和高。模板提取传输图如图2所示。其中:(a)为原始视频中提取的某帧,(b)为(a)做帧差图像(10倍亮度显示),(c)为(b)的二值化图像,(d)图上白色框表示自动选取出的掩模。

图2 模板的提取传输图
2.2 模板匹配
模板匹配是一种应用很广泛的定位方法,其主要过程为已知一个模板,在待检图像中通过滑动与模板同尺寸的框得到当前输入图像,利用一定数学方法统计各输入图像与原模板的差异,从而找出最佳匹配点。在帧差图Ct-中检测出多个模板,在Ct+中匹配出这些模板,就可以知道模板的运动速度。
本文采用式(6)来计算模板f在Ct+中的匹配程度:
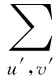
(6)
其中:f表示模板,f(u′,v′)表示模板在(u′,v′)处的灰度值;F为Ct+中的区域,F(u+u′,v+v′)表示左上角坐标为(u,v)的输入图像在(u′,v′)处的灰度值;R(u,v)表示模板与左上角坐标为(u,v)的输入图像的差异值;R(u,v)越小则以(u,v)为左上角坐标的输入图像块与模板差异越小。
展开式(6)可得:


(7)
在式(7)中第一项为模板各点的平方和,当模板已知时,为常量,所以本文只需计算后两项,而第二项为输入图像与模板的互相关项,第三项为输入图像块的能量。

(8)

(9)
Rs(u,v)=R1(u,v)-2R2(u,v)
(10)
本文取使得Rs(u,v)在取最小值的(u,v)作为模板f在Ct+中的最佳匹配坐标,即:
(u,v)*=arg(u,v)minRs(u,v)
(11)
为了提高计算Rs(u,v)的速度,可采用快速傅里叶变换计算式(10)。
2.3 流速计算
利用式(5)可获取到在Ct-上的模板bboxA,因为模板运动速度有限,则在很小的时间间隔有一定的运动范围,即匹配时选取一定的搜索范围可节省运算开销并提高精度。另一方面,考虑到模板匹配故有的检测漂移[15]问题,本文采用文献[15]的方法解决模板漂移问题,即先使用Ct-作为待检图像并找出模板的最佳匹配坐标,再使用Ct+作为待检图像中并找出模板的最佳匹配坐标,以这两个坐标作为位移计算的原始数据。对于某个模板,通过上述方法在Ct-上的最佳匹配坐标(r1,c1),在Ct+上的最佳匹配坐标(r2,c2),则将两个坐标的差作为模板真正的运动距离。为了得到可靠的运动速度,本文记录连续η帧上所有模板的位移(实验中η值取100)。
以横坐标为ω,纵坐标为模板位在范围[ω-ω0,ω+ω0](实验中ω0值取5)内出现的次数做统计。可见统计图为单峰分布,找出使得模板位移出现次数取得最大值的ω,统计在[ω-ω0,ω+ω0]范围内的剩余O组模板位移的平均值。
(12)
如图3所示,为某段河流视频令ω0=5时连续100帧的模板位移统计图,横坐标为ω值,纵坐标为[ω-ω0,ω+ω0]内模板位移出现的次数。
则水流表面运动速度:
(13)

图3 模板位移统计图
3 实验结果与数据分析
对于本文方法的准确性,需要通过实验进行验证,其方法是将本文算法计算得到结果与传统的机械旋转浆式水流测量仪的测量结果做对比。
3.1 实验设备及参数设置
本文实验采用的水流测量仪型号为LS1206B型旋浆式流速仪,其相对误差δ≤±5%,全线相对均方差|m|≤1.5%。视频采集使用的摄像机为佳能公司EOS1200D,镜头采用EF 75-300 mm Ⅲ,图片尺寸为1 920×1 088,帧率25即Δt=0.04 s。图像处理过程是在PC上完成,操作系统是Windows 7,算法运行环境是Matlab 2016。
3.2 低速河流速度测试与数据分析
为验证本方法的有效性,在自然条件下采集多段水流视频,并同时使用水流测量仪测量水流速度。在采集视频时,摄像机镜头轴线垂直于水面。经过实地采集,获得低速河流运动视频A、视频B,视频采集地点为兰州市银滩公园黄河支流。受试验条件限制,无法实地对中速河流进行测试,对中速河流通过进行模拟测试。本文认为河流在中速情况下,拍摄的视频中目标运动距离会变大;而在不同的拍摄距离下,拍摄的视频中的纹理特征会有不同的尺寸变化。由此本文通过两种方法来对其他速度情况与其它距离情况进行模拟。第一种是计算帧差图像时采用隔一帧做帧差的方法来模拟流速较高的情况,第二种是通过缩小视频尺寸来模拟拍摄距离较远的情况。
表1为河水表面流速测试误差统计表。其中,情形1与情形2为原始采集的视频A与视频B。情形3与情形4分别视频A与视频B隔帧采样后的视频。情形5与情形6为视频A与视频B的图像分别对宽和高缩小到原来0.5倍时的视频。

表1 河水表面流速测试误差统计表
其中:V0表示水流测量仪多次测量结果的平均值或通过模拟技术对视频处理后的计算值,V表示本方法或通过模拟技术对视频处理后的计算值,V表示本方法实验结果,k表示摄像机标定的放大系数,Δt表示帧间时差,l表示视频缩放系数,δ表示相对误差。
通过表1的情形1~2可以看出,本文方法对不同的视频都能进行检测,证明本文方法对低速河流具有普遍性。通过情形1与情形3、情形2与情形4对比,证明本文方法在目标位移变大时误差较小,表现良好。通过情形1与情形5、情形2与情形6对比,证明本文方法在目标尺寸变小时误差较小,表现良好。通过情形3~6可以看出,本文方法对中速河流也可以进行检测。综上所述,本文方法对中低速河流都能进行监测,并且结果稳定可靠,具有一定的可靠性与普遍性。
4 结 语
本文方法在通过帧间差分法与模板匹配相结合的技术对河流流动时产生的自然波纹进行跟踪,再联合摄像机标定来测算河水表面流速,基本实现了预期目标,是一种不受含沙量与漂浮物影响,设备和人力成本低且可持续实时监控的河水表面流速测量方法。本文通过实验与理论论证,证明基于机器视觉的水流速度测量方法是可行的,为进一步采用其他机器视觉处理方法测量水流速度提供了先期探索。实验结果表明,本文方法在单帧位移变大,目标尺寸变小的情况下,误差小于3%,效果良好,是一种可靠的河水表面流速测量方案。
[1] 韩予皖. 基于视频处理的河水流速监测系统设计[D]. 太原理工大学, 2013.
[2] 邓文浩, 唐立才, 张南锋,等. 基于改进的帧差法和Mean-shift结合的运动目标自动检测与跟踪[J]. 现代电子技术, 2016, 39(4):108-111.
[3] 於正强, 潘赟, 宦若虹. 一种结合帧差法和混合高斯的运动检测算法[J]. 计算机应用与软件, 2015,32(4):129-132,270.
[4] 张赛钰, 朱小玲, 汪衍广,等. 基于帧差法与Mean-shift算法相结合的运动熔滴识别与跟踪方法[J]. 上海交通大学学报, 2016,50(10):1605-1608.
[5] 刘青芳. 基于帧差法的运动目标检测方法研究[J]. 数字通信世界, 2015(11):54,120.
[6] 安云凤, 潘海鹏. 一种新的三帧差运动气泡检测方法[J]. 光电子·激光, 2016(9):963-972.
[7] 彭玉青, 李木, 高晴晴,等. 基于动态模板匹配的移动机器人目标识别[J]. 传感技术学报, 2016,29(1):58-63.
[8] 王雷, 姜久雷. 基于改进的模板匹配的设计模式自动识别[J]. 计算机工程与设计,2016,37(9):2429-2434.
[9] Fredriksson K, Mäkinen V, Navarro G. Rotation and lighting invariant template matching[J].Information & Computation, 2004,205(7):1096-1113.
[10] 唐琎, 李青. 一种快速的模板匹配算法[J]. 计算机应用, 2010, 30(6):1559-1561.
[11] 李超, 于飞, 康晓军. 一种模板匹配的快速实现方法[J]. 航天返回与遥感, 2016,37(1):63-70.
[12] 李世扬, 储泽楠. 一种视频图像目标平移运动估计算法[J]. 计算机应用与软件, 2015, 32(12):184-187,200.
[13] 修彬, 李成龙, 汤进,等. 一种基于运动估计的红外目标跟踪方法[J]. 计算机工程与应用, 2014,50(12):125-128.
[14] 禹晶, 苏开娜. 块运动估计的研究进展[J]. 中国图象图形学报, 2007, 12(12):2031-2041.
[15] 潘吉彦, 胡波, 张建秋. 抑制模板漂移的目标跟踪算法[J].电子学报, 2009,37(3):622-627.
MEASURINGSURFACEVELOCITYOFRIVERFLOWBASEDONIMAGESOFFRAMEDIFFERENCEANDTEMPLATEMATCHING
Zhao Xiaogang1Feng Quan1*Wang Shuzhi21
(CollegeofEngineering,GansuAgriculturalUniversity,Lanzhou730070,Gansu,China)2(SchoolofElectricalEngineering,NorthwestUniversityforNationalities,Lanzhou730030,Gansu,China)
There are some limitations in traditional velocity measure methods of river flow. For example, sediment concentration, floating objects and the cost of device and human resource are too high. In order to overcome the limitations, this paper proposes a method to measure the surface velocity of the river flow based on computer vision. We analyzed the relationship between image space and real world space, and derived the physical velocity from the image velocity. We captured the video of river by a camera whose optic axis was perpendicular to the surface of the river. The frame difference method was used to produce difference image in which the salient moving regions were detected as templates. In the succeeding difference image, the template matching algorithm was employed to find out the regions matched those template best, indicating the templates’ movement. The shift of a template between two images was evaluated by the pair of the template and the corresponding region and used to calculate the velocity of the template. The experimental results show that the proposed method can evaluate the surface velocity effectively and accurately for smooth flow. The error is lower than 3%, and the flow velocity can be monitored continuously.
Flow velocity measurement Template matching Video processing Frame difference method
TP3
A
10.3969/j.issn.1000-386x.2017.09.014
2016-12-28。国家自然科学基金项目(61461005)。赵晓刚,硕士生,主研领域:图像处理,模式识别。冯全,教授。王书志,副教授。
