基于岭回归的气体预警穿戴系统的灵敏度校正

袁方红，许武军,2，赵海森

(1. 东华大学 信息科学与技术学院，上海 201620; 2. 数字化纺织服装技术教育部工程研究中心，上海 201620)

基于岭回归的气体预警穿戴系统的灵敏度校正

袁方红1，许武军1,2，赵海森1

(1. 东华大学 信息科学与技术学院，上海 201620; 2. 数字化纺织服装技术教育部工程研究中心，上海 201620)

在气体预警穿戴系统中，使用电化学气体传感器来采集环境中CO气体的浓度。由于电化学气体传感器的灵敏度随着温度有着非常显著的变化，为了提高传感器的检测精度，采用一种基于岭回归算法对电化学气体传感器进行灵敏度校正。开发算法的软件工具采用Python语言进行编程，根据传感器和温度关系的已有关系样本对其进行拟合，并对拟合结果进行交叉性验证分析。通过分析对比可知，基于岭回归算法的电化学气体传感器灵敏度曲线拟合效果好于普通的最小二乘法拟合。

气体预警穿戴系统；电化学气体传感器；灵敏度校正;岭回归；Python

0 引言

电化学气体传感器是把测量对象气体在电极处氧化或还原而测电流，得出对象气体浓度的探测器。且其具有体积小、结构简单、选择性及响应快等特点，被广泛运用于气体泄漏等环境监测中。但由于气体传感器对温度有一定的敏感度, 当工作环境温度发生变化时, 致使传感器的零点和灵敏度发生变化，从而造成输出值随环境温度变化，导致测量出现附加误差[1]。在实际监测环境中，被检测的气体大部分为有毒气体，微小的误差便可能造成巨大的损失，因此根据温度变化对传感器的灵敏度进行校正十分必要。

对电化学气体传感器进行灵敏度校正，可以采用硬件和软件校正。但由于硬件电路校正调试困难、精度低、适用性差等缺点，通常采用软件进行校正。软件校正可采用最小二乘法、回归算法、神经网络等方法。通过BP神经网络对气体和温度传感器进行有效的数据融合，在特定浓度范围内消除温度对气体传感器交叉敏感的影响，从而改善了气体预警装置的检测精度[2]。考虑气体传感器所在的硬件平台及处理器的运算能力，本文将采用岭回归方法进行校正。这种方法相对于简单的最小二乘法一元线性拟合提高了校正精度，并且比一些人工智能算法降低了对处理器运算能力的要求，能更好地运用于实际工程中去。

1 系统介绍

1.1穿戴式气体预警系统

穿戴式毒害气体预警系统由本地服务器、气体预警装置和无线路由组成[3]。其中气体预警装置包括系统平台(微控制器、无线连接和电源管理)，传感模块(EC气体传感模块和温湿度传感模块)和执行模块(视觉告警模块、听觉告警模块、触觉告警模块和气体交换模块)。本地服务器和气体预警装置通过AP连接，气体预警装置将采集的气体浓度转换为电流信号，并经过信号放大、模数转换以及气体浓度换算，将换算数据发送到上位机中[3]。

其中系统平台的微控制器采用TI公司的FRAM系列MSP430单片机MSP430FR5739[3]。考虑到运算能力不足，本文将MSP430向PI Zero进行迁移，以解决实时计算能力的问题。

树莓派PI Zero， 使用Broadcom BCM2835 1 GHz处理器，拥有512 MB RAM， 支持micro SD存储槽、mini-HDMI接口，1 080 p/60 fps输出和microUSB接口传输数据及充电，并拥有40针的GPIO。电化学传感器采用CO1000 Micro3。

气体预警装置框图如图1所示。

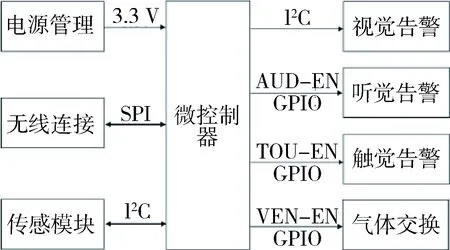
图1 穿戴式毒害气体预警系统气体预警装置框图

1.2岭回归算法介绍

随着互联网人工智能的发展，机器学习已经成为当今科技领域的热门内容，被用来处理生活中不断爆发的数据问题。而岭回归[4]便属于机器学习中的一种常见算法。岭回归是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法[4]。

岭回归是线性回归的一种补充。对于线性回归来说，假设x为输入矩阵，y为输出矩阵，回归系数矩阵为ω，目标就是要找出使误差最小的ω。其平方误差为：

(1)

用矩阵可表示为：(y-xω)T(y-xω),对ω求导，解出：

(2)

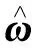
岭回归就是在矩阵xTx上加一个λI，从而使矩阵非奇异，进而对xTx+λI求逆。其中I是一个单位方阵[4]。因此回归系数变为:

(3)

岭回归最先用于处理特征多于样本的情况，现在也用于在估计中加入偏差，从而得到更好的估计[4]。

1.3软件平台简介

系统硬件平台为PI Zero，PI Zero搭载Linux系统，支持Python语言。且由于Python语法清晰，易于操作文本文件，且使用广泛，因此选择Python作为实现算法的编程语言。

Python是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。Python的设计具有很强的可读性，相比其他语言经常使用英文关键字以及其他语言的一些标点符号，它具有更有特色的语法结构[5]。

其中Scipy和Numpy等许多科学函数都实现了向量和矩阵操作，也可运用matplotlib绘制2D、3D曲线图形。MATLAB等高级程序语言虽然也可以进行矩阵操作并构造机器学习应用，但MATLAB的软件费用过高，虽然也有比较适合MATLAB的第三方插件，但是没有一个有影响力的大型开源项目[4]。

Java和C 也拥有数学矩阵库，但是这些语言的编写效率较低，完成一个简单的工作就要花费大量时间。

2 基于岭回归算法的灵敏度校正

2.1利用岭回归法的一般步骤

(1)收集数据；

(2)准备数据；

(3)分析数据：可视化并观察数据；

(4)训练算法：采用岭回归算法构建不同的模型；

(5)测试算法：使用交叉验证来测试不同的模型；

(6)使用算法。

2.2电化学气体传感器及其灵敏度随温度变化曲线

根据CO1000 Micro3使用手册可得知，电化学气体传感器的灵敏度随温度变化的曲线如图2。

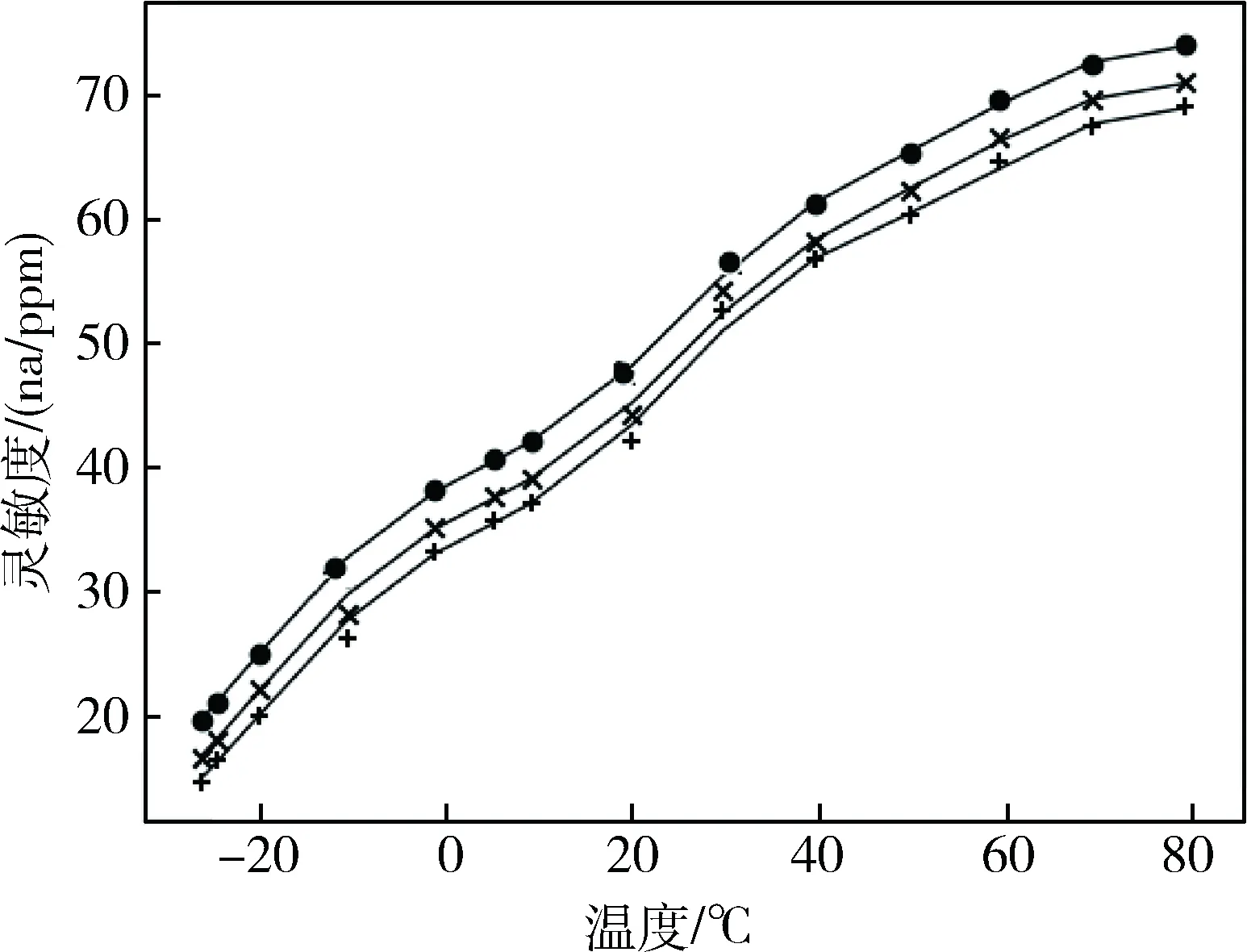
图2 CO1000 Micro3 灵敏度和温度的关系

根据图2，对传感器进行数据读取标定(平均值)。如表1所示。将样本数据制作成文本文件，并命名为Sensitivity.txt文件。

其中x为输入矩阵，为温度值；输出矩阵为y，是灵敏度。x是一个14×2的矩阵，因为计算灵敏度系数需要输入矩阵的初始状态，所以需要定义温度的初始值，这个值可以是任意常数，由前文公式可知，设定初始值不会对结果造成太大影响。

第一列的初始值不能为相同值，若第一列为相同数值，在对角权重矩阵的求逆过程中会出现问题，导致xTx成为非奇异矩阵，无法求逆，违背了岭回归算法的初衷。

2.3算法流程

算法流程如图3所示。

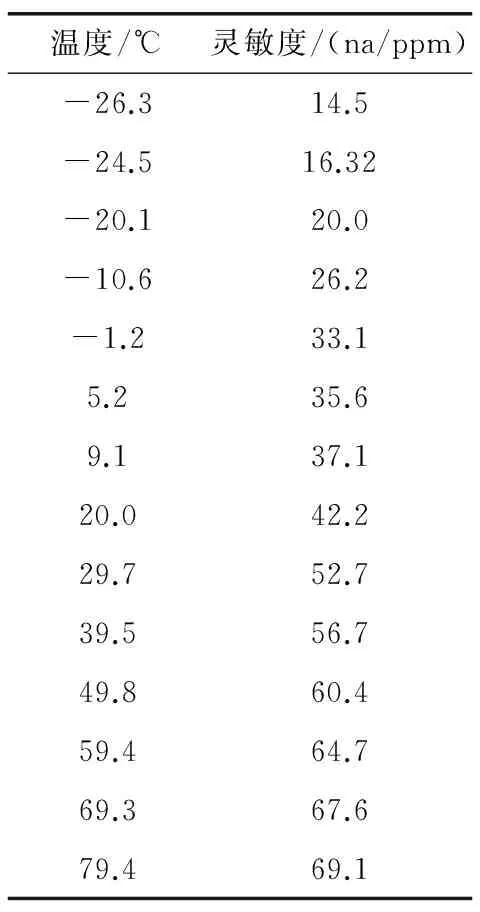
表1 传感器灵敏度与温度的关系

图3 算法流程图

将数据导入函数。

(1)定义文件读取函数：

def loadDataSet(fileName):

(2)定义曲线拟合函数：

def standRegres(x,yArr):

(3)创建对角权重矩阵：

def lwlr(testPoint,x,y,k=1.0):

(4)遍历数据集：for循环遍历

输入的参数k控制衰减的速度。在权重矩阵计算完之后，可以得到对回归系数的一个估计。

(5)定义计算回归系数函数：

def ridgeRegres(xMat,yMat,la=0.2):

(6)定义测试λ函数：

def lwlrTest(testArr,xArr,yArr,k=1.0):

由于增加了λI，在普通线性回归产生计算错误时，岭回归仍然能继续工作。

(7)创建训练集和测试集：

def crossValidation(xArr,yArr,numVal=10):

(8)用训练时的参数将测试数据标准化：

for k in range(30):

matTestX=mat(testX); matTrainX=mat(trainX)

meanTrain = mean(matTrainX,0)

varTrain = var(matTrainX,0)

matTestX= matTestX-meanTrain)/varTrain

在基于岭回归的局部加权回归中若对缩减系数设置过小，将出现过拟合现象。由于本文数据较少，因此其系数不宜小于1。

另外，岭回归由于引入了λI，所以，λ的取值也将对拟合曲线的精确度产生影响。对50个不同的λ调用岭回归函数，得到了对应的回归系数，如图4所示。

图4 回归系数与λ的关系

由图4可以看到，当λ很小时，回归系数是与线性回归一致的原始值；当λ很大时，其系数逐步缩减为0。在横坐标上，当λ取中间部分的值时，可以得到较好的预测效果。为了定量地找出最佳的λ，还需对模型进行交叉验证。

最小二乘法的回归系数：

>>> regression.standRegres(a,b)

matrix([[ 28.09934246], [0.80421217]])

通过交叉验证的岭回归系数:

>>> regression.crossValidation(a,b)

zui jia mo xing:

[[ 1.00676092 0.50575633]]

bu bian zhi: 32.0155989087

通过比较可以看出，岭回归的回归系数相对于最小二乘法进行了缩减，提高了预测精度。

3 结果分析

将岭回归算法与逐步加权回归相结合，加入“惩罚项”来对回归系数进行限制，并通过逐步加权回归的引入,理论上会比最基本的最小二乘法线性回归得到更精确的拟合效果。本文将岭回归的结果与最小二乘法进行比较，来观察具体效果。

3.1最小二乘法效果图

使用matplotlib函数，绘制图形，如图5所示。

图5 最小二乘拟合效果图

3.2基于岭回归的逐步加权回归效果图

基于岭回归的逐步加权回归如图6所示，所有数据点均位于拟合曲线上。

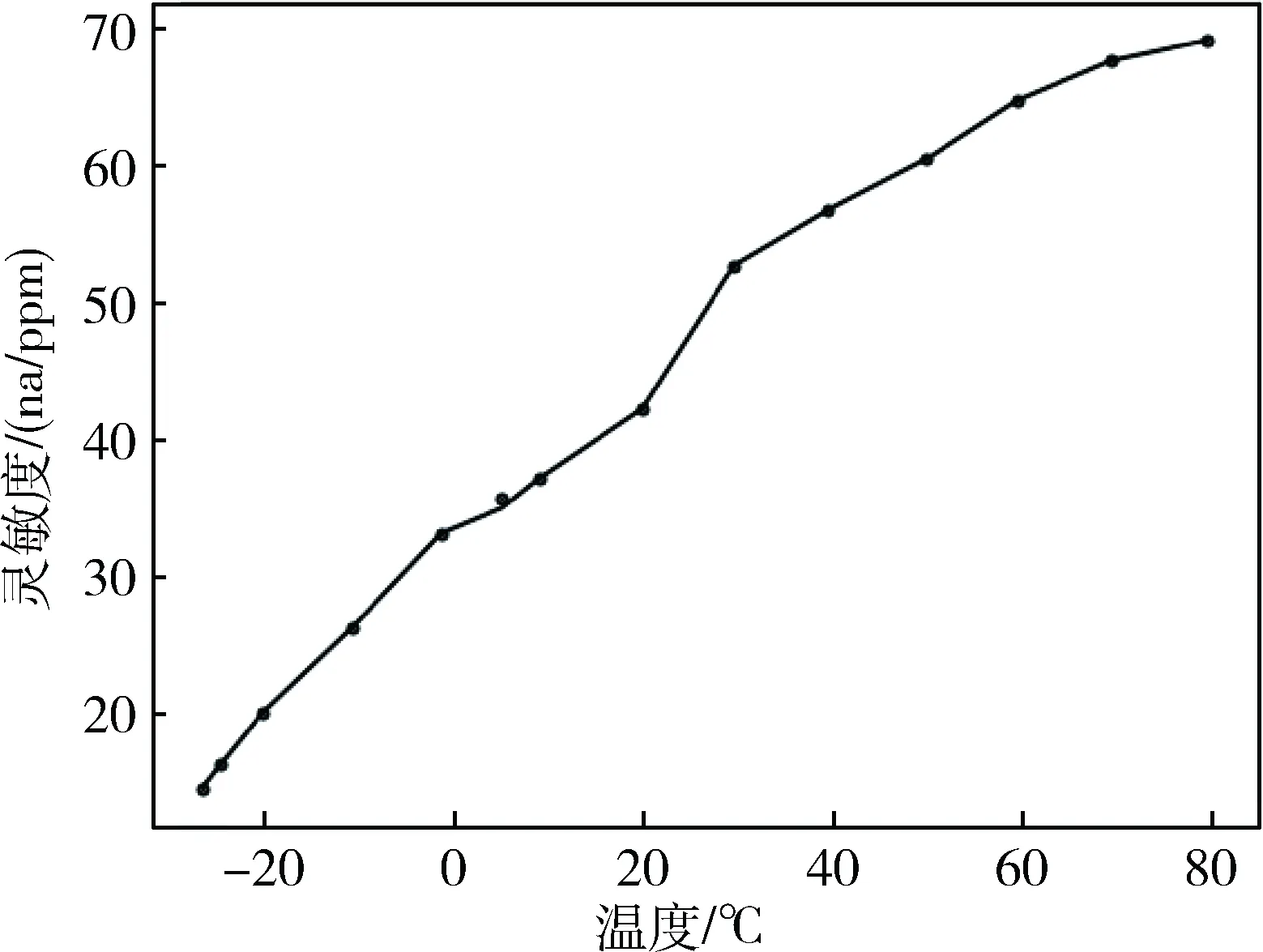
图6 基于岭回归的逐步加权回归效果图

3.3分析

由图5、图6可知，最小二乘法接近于直线拟合，对曲线的拟合不尽理想，而基于岭回归的逐步加权则将原始数据充分拟合，使原始数据均位于拟合曲线上，取得了更好的拟合效果。

[1] 史雪飞,冯淑红.DS1820芯片在电化学传感器温度补偿中的应用[J] .工业计量, 2006, 16(2):29-31.

[2] 于浩,许武军,袁方红,等.基于神经网络的气体预警穿戴系统的温度补偿[J]．微型机与应用，2016，35(15): 18-20，23．

[3] 曾凯.穿戴式作业现场毒害气体预警系统[D].上海：东华大学，2015.

[4] HARRINGTON P.机器学习实战[M].李锐,李鹏,曲亚东,等译.北京:人民邮电出版社,2013.

[5] 自然学堂.Python基础教程[EB/OL].[2017-04-01].http://www.ziqiangxuetang.com/python/python-intro.html.

Sensitivity correction in wearable gases alarm system based on ridge regression

Yuan Fanghong1, Xu Wujun1,2, Zhao Haisen1

(1. College of Information Science and Technology, Donghua University, Shanghai 201620, China;2. Engineering Research Center of Digitized Textile & Fashion Technology, Ministry of Education, Shanghai 201620, China)

The electrochemical gas sensor is used to get the concentration of CO in wearable gases alarm system. Science the sensitivity of electrochemical gas sensor changes much more when the environment temperature has changed, and it will have a bad effect on the accuracy of electrochemical gas sensor. So this paper presents a method which is based on ridge regression to regulate the sensitivity of electrochemical gas sensor. The software which we use is python. And we carry out linear fitting according to the relationship between the sensor and the temperature from the samples, and the fitting results are cross checked and analyzed. The results show that the sensitivity curve of the electrochemical gas sensor based on the ridge regression algorithm is better than that of the ordinary least squares fitting.

wearable gases alarm system; electrochemical gas sensors; sensitivity correction;ridge regression; Python

TP391

：A

10.19358/j.issn.1674- 7720.2017.17.023

袁方红，许武军，赵海森.基于岭回归的气体预警穿戴系统的灵敏度校正[J].微型机与应用，2017,36(17)：79-81,85.

2017-04-10)

袁方红(1990-)，女,硕士研究生，主要研究方向：控制工程。许武军(1972-)，通信作者，男，博士，副教授，硕士生导师，主要研究方向：穿戴电子与智能服装，短距无线通信，嵌入式计算与机器视觉，卫星导航与组合定位。E-mail:wujun.hsu@gmail.com。赵海森(1993-)，男，硕士研究生，主要研究方向：控制工程。