钢管桩码头抗震设计中曲率延性指标的计算
2017-09-22陶桂兰乔赵阳阮健
陶桂兰,乔赵阳,阮健
钢管桩码头抗震设计中曲率延性指标的计算
陶桂兰1,乔赵阳1,阮健2
(1.河海大学港口海岸与近海工程学院,江苏南京210098;2.中交第二航务工程勘察设计院有限公司,湖北武汉430071)
能够快速方便的计算得到高桩码头的曲率延性系数,对基于性能的高桩码头抗震设计具有重要意义。应用纤维模型法对高桩码头所采用的钢管桩进行了弯矩-曲率分析,计算了不同设计参数下钢管桩截面的等效屈服曲率以及不同极限状态下钢管桩截面的曲率,讨论了不同轴压比、壁厚对钢管桩截面等效屈服曲率和极限曲率的影响。在考虑了轴压比、壁厚和管径等因素的情况下,对钢管桩截面曲率进行拟合,获得了钢管桩的等效屈服曲率的计算回归公式以及不同设计极限状态下的曲率的计算回归公式。通过算例分析验证了所得回归公式的可靠性。同时导出了不同极限状态下钢管桩截面的曲率延性系数的计算公式,供工程设计人员参考。
钢管桩码头;抗震设计;弯矩曲率分析;等效屈服曲率;极限曲率;曲率延性系数;回归公式
0 引言
近年来,基于性能的抗震设计方法已在建筑、公路桥梁领域逐步得到应用[1-2],曲率延性系数[3]是工程结构基于性能的抗震设计中一种十分重要的评价指标,一般工程结构的曲率延性系数可通过截面的极限曲率和等效屈服曲率计算得到。在港口工程领域,美国已于2014年实施新的抗震设计规范《防波堤及码头抗震设计准则》[4],其给出了高桩码头钢筋混凝土桩基的曲率延性需求的计算公式,但并未就钢管桩码头做出规定。此外,国内阮健等[5]讨论了高桩码头预应力高强度混凝土管桩(PHC)极限曲率的计算方法。目前,国内关于高桩码头钢管桩基于曲率延性指标的抗震设计的研究较少,现行规范[6]对此也尚未涉及,有必要对此开展深入研究。鉴此,针对我国常用的钢管桩码头结构形式,研究了确定高桩码头钢管桩的等效屈服曲率及3种极限状态下的曲率的计算方法,并拟合得到相应的曲率计算回归公式,同时,进一步推导了曲率延性系数的计算公式,为基于性能的钢管桩码头抗震设计提供依据。
1 计算方法
1.1 计算简图
图1为钢管桩截面曲率的计算简图(图中着c为钢管边缘的压应变;着s为钢管边缘的拉应变;孜为受压区高度系数;D为截面高度)。
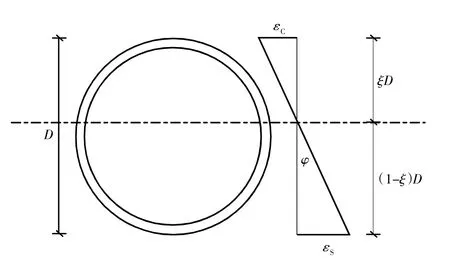
图1 钢管桩截面曲率计算简图Fig.1Section curvature calculation of steel pipe piles
由图1可得桩截面曲率渍计算公式为:

1.2 等效屈服曲率及极限曲率
钢管桩截面等效屈服曲率的定义[7]如图2所示,钢材弯矩曲率(M-渍)曲线可以等效成为双线性模型,假定截面屈服后的刚度为0,将原点与受拉钢材首次屈服点(渍y忆,My忆)的连线视为初始弹性阶段,调整塑性阶段水平线的位置使得图2中两块阴影部分的面积相等,等效屈服曲率即为渍y。
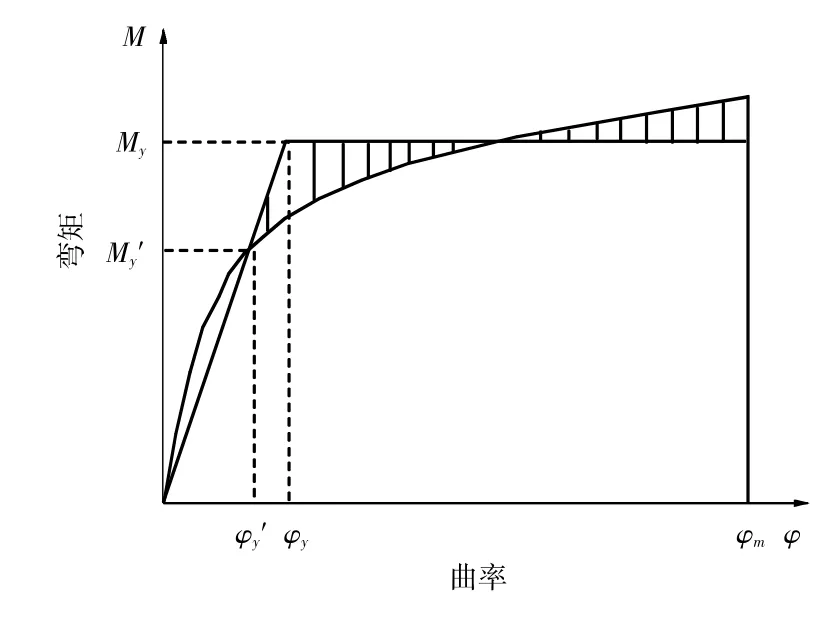
图2 等效屈服曲率的定义Fig.2Definition of equivalent yield curvature
本文中的不同极限状态的曲率渍m对应于一定的性能目标[8]。对于钢管桩结构的设计极限状态,美国码头抗震设计规范Seismic Design of Piers and Wharves[4]规定了3个地震动水准:运营水平地震(OLE)、偶遇水平地震(CLE)、设计水平地震(DE)。其性能目标分别为:OLE地震发生后,码头可继续使用;CLE地震发生后,码头经修复可继续使用;DE地震发生后,码头能够保障生命安全,不倒塌。定义相应的3种极限状态分别为正常使用极限状态、损伤控制极限状态和不倒塌极限状态(分别记为A极限状态、B极限状态、C极限状态)。文献[4]用钢管桩的拉应变定量表示不同极限状态,钢管桩桩基材料不同极限状态下应变限值的规定见表1。
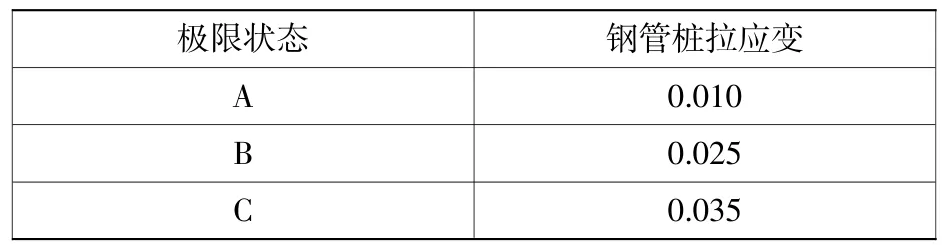
表1 钢管桩材料应变限值Table 1Strain limits of steel pipe piles
1.3 应力-应变关系
在受拉和受压的情况下,钢材具有相同的应力应变关系,本文所研究的钢管桩的钢材型号均为Q345B,屈服强度为Re=345 MPa,弹性模量为Es=2伊105MPa,应力-应变关系采用理想弹塑性模型。
1.4 弯矩曲率分析
使用通用截面分析软件Xtract进行截面弯矩-曲率分析[9]。该软件基于纤维面模型将截面离散为一系列的纤维单元。
建模过程中的假定主要有:l)钢管桩的横截面在受力变形后仍为平面,并且同变形后的钢管桩轴线垂直;2)钢管桩的剪切变形可以忽略;3)钢管桩扭转的影响可以忽略。
通过弯矩曲率分析可得到不同设计参数下钢管桩截面的等效屈服曲率和极限曲率。
2 截面等效屈服曲率的计算分析
2.1 计算工况
钢管桩截面外径D取800 mm、1 000 mm和1 200 mm,管桩壁厚t取14 mm、16 mm、18 mm和20 mm,轴压比浊取0、0.1、0.2、0.3、0.4,共60种计算工况。
2.2 截面等效屈服曲率影响因素分析
将3种桩径钢管桩的截面等效屈服曲率数据根据管径进行标准化[10],令截面曲率与钢管桩截面外径的乘积为K,即K=渍·D,从而可以消除截面尺寸的影响,取3种钢管桩截面对应的K值的平均值。等效屈服曲率随轴压比和壁厚的变化分别如图3、图4所示。

图3 等效屈服曲率随轴压比的变化Fig.3Variation of equivalent yield curvature with axial compression ratio

图4 等效屈服曲率随壁厚的变化Fig.4Variation of equivalent yield curvature with wall thickness
从图3、图4可以明显看出,钢管桩截面的等效屈服曲率受轴压比和壁厚的影响很小,可忽略不计。
2.3 截面等效屈服曲率公式拟合
利用Origin软件对钢管桩截面的等效屈服曲率进行拟合,在轴压比0~0.4,壁厚14~20 mm范围内,钢管桩截面的等效屈服曲率可由式(2)近似求得:

式中:渍y为截面的等效屈服曲率;D为截面外径,m。
为验证式(2)是合理的,利用式(2)计算了外径为900 mm、壁厚18 mm的钢管桩在轴压比0、0.1、0.2、0.3、0.4下的等效屈服曲率,并与Xtract软件纤维模型法曲率分析值进行了比较,比较结果表明所拟合公式误差均控制在2%以内,利用其进行截面等效屈服曲率的计算可满足工程需要。由于在上述分析过程中,钢材采用Q345B,仅对一定范围的轴压比和壁厚进行了研究,因此,在使用拟合公式(2)时,宜考虑轴压比和壁厚的适用范围,我国高桩码头常用钢管桩都在这个范围内。
3 截面极限曲率的计算分析
[4]对高桩码头A、B、C极限状态对应的材料极限应变限值的规定,计算3种极限状态下钢管桩截面的曲率。
3.1 计算工况
钢管桩截面外径D取800 mm、1 000 mm和1 200 mm,壁厚t取14 mm、16 mm、18 mm和20mm,轴压比浊取0、0.1、0.2、0.3、0.4,控制计算的钢材拉应变着s取0.01、0.025和0.035,共180种计算工况。
3.2 截面极限曲率影响因素分析
将3种桩径钢管桩的截面极限曲率数据根据桩径进行标准化[10],取3种管桩截面对应的K值的平均值,依据5种轴压比对应的壁厚作图,得到3种极限状态下曲率随钢管桩壁厚的变化规律如图5。
从图5可以看出,壁厚的变化对极限状态下的截面曲率基本无影响,所以将4种壁厚下的截面的K值取平均值,仅对轴压比的影响进行分析。依据对应的轴压比进行作图,得到3种极限状态截面曲率变化规律,结果如图6所示。
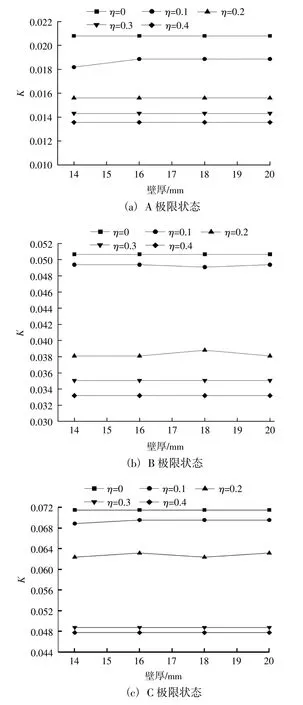
图5 3种极限状态下曲率随壁厚的变化Fig.5Variation of the curvature with the wall thickness under 3 limit states

图6 3种极限状态曲率变化曲线Fig.6Curvature change curve under 3 limit states
从图6可以看出,对应于A极限状态、B极限状态和C极限状态的截面曲率依次增大。3种极限状态的截面曲率都随轴压比的增大而减小,A极限状态下的截面曲率随轴压比的变化较平缓,近似呈线性关系;B极限状态的截面曲率随轴压比的变化也比较平缓,在轴压比0.1~0.2的范围内变化的幅度相对于其他轴压比的情况下较大;C极限状态的截面曲率随轴压比的变化也比较平缓,在轴压比0.2~0.3的范围内变化的幅度相对于其他轴压比的情况下较大。
3.3 截面极限曲率公式拟合
从图6的分析结果可以看出,轴压比是钢管桩极限状态下的截面曲率的重要影响因素,考虑轴压比的影响,对钢管桩在A、B、C极限状态下的截面曲率进行线性拟合,式(3)、式(4)、式(5)分别为A、B和C极限状态下的曲率计算公式的拟合结果:
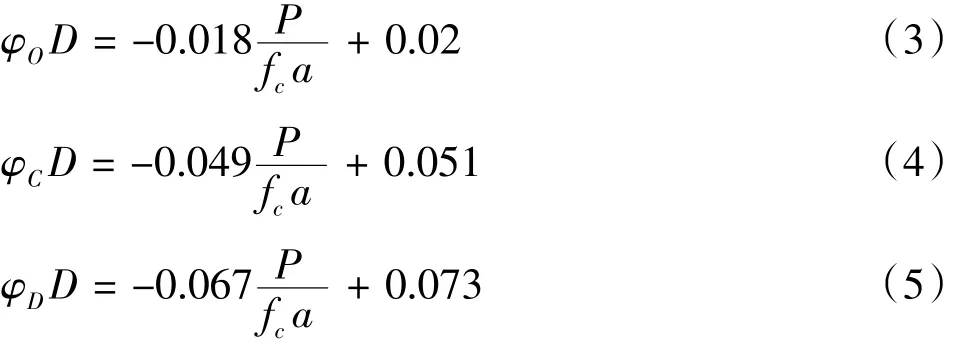
式中:D为钢管桩截面外径;渍O、渍C、渍D分别为A、B、C 3种极限状态下的截面曲率;a为截面面积;fc为钢管桩屈服强度设计值;P为轴压力;浊为轴压比。
为验证式(3)、式(4)和式(5)是合理的,利用3个公式计算了外径为900 mm、壁厚18 mm的钢管桩在轴压比0、0.1、0.2、0.3、0.4下对应3种极限状态下的曲率值,并与Xtract软件纤维模型法曲率分析值进行了比较,比较结果表明所拟合公式误差均控制在8%以内,其精度可满足实际工程极限状态的截面曲率计算的需要,且我国高桩码头常用钢管桩的轴压比和壁厚均在上述分析数据的范围内。
4 曲率延性系数的计算
参考文献[3]对钢管桩截面的曲率延性系数的定义为:

式中:滋渍为钢管桩截面的曲率延性系数;渍m为钢管桩截面的极限曲率;渍y为钢管桩截面的等效屈服曲率。
将式(2)和式(3)、式(4)、式(5)代入曲率延性系数的计算公式(6),得到3种极限状态下曲率延性系数的计算公式如下:

为验证所推导的公式是合理的,利用式(7)、式(8)和式(9)计算了外径为900 mm、壁厚18 mm的钢管桩在轴压比0、0.1、0.2、0.3、0.4下对应3种极限状态下的曲率延性系数,并与Xtract软件纤维模型法曲率延性系数分析值进行了比较,比较结果表明所拟合公式误差均控制在10%以内,其精度可满足实际工程极限状态的截面曲率延性系数计算的需要,且我国高桩码头常用钢管桩的轴压比和壁厚均在上述分析数据的范围内。
5 结语
采用基于纤维模型法的Xtract软件,计算了高桩码头中不同设计参数下钢管桩截面的等效屈服曲率,同时,参照美国最新的码头抗震规范中对于不同极限状态下应变限值的规定,计算了3种极限状态下钢管桩截面的曲率,主要得到以下结论:
1)轴压比和壁厚的变化对等效屈服曲率的影响可忽略不计;壁厚的变化对极限状态下的截面曲率基本无影响,3种极限状态的截面曲率都随轴压比的增大而减小,正常使用极限状态下的截面曲率随轴压比的变化较平缓,近似呈线性关系;损伤控制极限状态和不倒塌极限状态下的截面曲率随轴压比的变化也比较平缓,但分别在轴压比0.1~0.2、0.2~0.3范围内变化的幅度相对于其他轴压比的情况下稍大。
2)利用Origin软件拟合得到钢管桩截面等效屈服曲率的计算公式(2)及不同极限状态下截面曲率的计算公式(3)、公式(4)、公式(5),并进一步推导得到不同极限状态下钢管桩曲率延性系数的计算公式(7)、公式(8)、公式(9),并通过算例验证了上述公式的合理性,所拟合公式可为基于性能的钢管桩码头抗震设计中曲率延性指标的确定提供参考。
参考文献:
[1]李建中,管仲国.基于性能桥梁抗震设计理论发展[J].工程力学,2011,28(S域):24-30.
LI Jian-zhong,GUAN Zhong-guo.Performance-based seismic design for bridges[J].Engineering Mechanics,2011,28(S域):24-30.
[2]邓明科,梁兴文,孙宏哲.高性能混凝土剪力墙基于性能的抗震设计截面延性分析[J].工程力学,2010,27(S1):177-182.
DENG Ming-ke,LIANG Xing-wen,SUN Hong-zhe.Curvature ductility analysis of high performance concrete share wall in performance-based seismic design[J].Engineering Mechanics,2010, 27(S1):177-182.
[3]叶爱君,管仲国.桥梁抗震[M].2版.北京:人民交通出版社,2002:83-84.
YE Ai-jun,GUAN Zhong-guo.Seismic design of bridges[M].2nd ed.Beijing:China Communications Press,2002:83-84.
[4]American Society of Civil Engineers.Seismic design of piers and wharves[S].Virginia:American Society of Civil Engineers,2014.
[5]阮健,陶桂兰.高桩码头PHC管桩设计极限状态的曲率计算方法[J].水电能源科学,2016,34(4):92-95.
RUAN Jian,TAO Gui-lan.Curvature calculation method of PHC pipe pile used in high pile wharf under design limit states[J].Water Resources and Power,2016,34(4):92-95.
[6]JTS 146—2012,水运工程抗震设计规范[S]. JTS 146—2012,Code for seismic design of water transport engi原neering[S].
[7]Caltrans,Seismicdesigncriteria[S].Version 1.2,Sacramento, California:Califofnia Department of Transportation(CALTRANS), 2001.
[8]Port of Long Beach,wharf design criteria[S].Version 3.0,Long Beach:CA,2012.
[9]CHADWELL C B,IMBSEN R A.XTRACT:A tool for axial force-ultimatecurvatureinteractions[C]//StructuresCongress.ASCE, 2004.
[10]刘媛.钢筋混凝土桥墩的目标位移及基于性能的抗震设计[D].西安:长安大学,2009.
LIU Yuan.The target displacement of reinforced concrete pier and theperformance-basedseismicdesign[D].Xi忆an:Chang忆an University,2009.
Calculation of curvature ductility index in seismic design of steel pipe pile wharf
TAO Gui-lan1,QIAO Zhao-yang1,RUAN Jian2
(1.College of Harbor,Coastal and Offshore Engineering,Hohai University,Nanjing,Jiangsu 210098,China; 2.CCCC Second Harbor Consultants Co.,Ltd.,Wuhan,Hubei 430071,China)
For the seismic design of high pile wharf based on performance,it is very important to calculate expediently the curvature ductility factor of high pile wharf.The moment curvature analysis of steel piles used in high pile wharf was carried out by using the fiber model method,and then,the equivalent yield curvature under different design parameters and the curvature under different limit states of steel pipe pile sections were calculated.At the same time,the effects of axial compression ratio and wall thickness on the equivalent yield curvature and ultimate curvature of steel pipe pile sections were discussed.After consideration of axial compression ratio,wall thickness and pipe diameter,the cross section curvature of steel pipe pile was fitted,and the calculation regression formula of equivalent yield curvature and the calculation regression formulas of ultimate curvature under different design limit states were obtained.The reliability of the obtained regression formula was verified by example analysis.Finally,the calculation formula of the curvature ductility factor of steel pipe pile sections under different limit states was derived as reference for engineering designers.
steel pipe pile wharf;seismic design;moment curvature analysis;equivalent yield curvature;ultimate curvature; curvature ductility factor;regression formula
U656.113
A
2095-7874(2017)09-0027-05
10.7640/zggwjs201709006
2017-02-25
2017-05-05
江苏省基础研究计划(自然科学基金)(BK20151498)
陶桂兰(1962—),女,江苏南通人,副教授,博士,主要从事港航工程结构研究。
*通讯作者:乔赵阳,E-mail:zhaoyangqiao27@163.com
