基于D-S证据理论的发动机部件性能降级量化融合研究

魏 芳，梁茂宗，马晶玮，周登极，张会生

(1.中国航发商用航空发动机有限责任公司，上海201108；2.上海商用飞机发动机工程技术研究中心，上海201108；3.上海交通大学燃气轮机研究院，上海200240)

基于D-S证据理论的发动机部件性能降级量化融合研究

魏 芳1，2，梁茂宗3，马晶玮1，2，周登极3，张会生3

(1.中国航发商用航空发动机有限责任公司，上海201108；2.上海商用飞机发动机工程技术研究中心，上海201108；3.上海交通大学燃气轮机研究院，上海200240)

针对多方法计算所得发动机部件性能降级无法直接应用Dempster-Shafer(D-S)证据理论融合的问题，提出一种实现降级参数量化融合的方法。以一段时间内计算结果作为样本，融合性能模型输出结果和神经网络输出结果，通过划分区间统计样本落入区间的频率构造基本概率赋值(BPA)，从而实现性能降级的量化融合。对比了独立区间划分法和嵌套区间划分法两种BPA构造方法的融合结果，得出了嵌套区间划分法构造BPA具有更适合量化融合的主要结论。

航空发动机；D-S证据理论；性能降级；基本概率赋值；嵌套区间划分；量化融合；信息融合

1 引言

航空发动机使用过程中，气路部件因受高温、高压、高速旋转、封严磨损和外物冲击等因素的影响性能发生退化，与运行初期相比效率和流通能力明显下降，进而导致整机性能退化。发动机部件性能降级是发动机健康管理中必须监测的参数，可通过测量的温度、压力、转子转速和燃油流量等相关参数间接反映，检测这些参数的变化可实现对气路部件的监视或故障诊断。自Urban提出气路分析法利用测量参数进行气路故障诊断后，相继有大量学者研究不同的气路故障诊断方法及应用。其中，Li[1-2]研究了GPA、GA方法用于燃气涡轮发动机气路故障诊断；张鹏[3]以性能参数作为输入，利用卡尔曼方法对航空发动机气路故障进行诊断；翁史烈[4]以性能参数作为输入，通过模糊神经网络方法对燃气轮机故障进行诊断。由于不同诊断方法在诊断阶段、诊断信息源及诊断结果方面有不同的适用范围，需解决如何在维修决策中应用这些诊断结果、降低故障诊断的虚警率。信息融合可对多源信息在一定准则下进行自动分析综合，通过对不同发动机气路故障诊断算法结果的决策层融合，得到比单一方法诊断结果更可靠的状态估计或推理决策信息。资料显示，GEnx发动机故障诊断中就采用了信息融合技术。

决策层融合最常用的方法有贝叶斯推理和D-S证据理论两种，由于贝叶斯推理需要先验概率的输入，因此决策层融合更多地采用D-S证据理论的方法。D-S证据理论从思想方法上可看作是一种基于不精确概率进行推理的理论和方法[5]。Wen[6]使用D-S证据理论对不同特征数据进行决策融合，获取不同故障模式发生的概率；Dewallef[7]研究了利用贝叶斯网络(BBN)与卡尔曼滤波方法互相融合进行发动机气路故障诊断的方法；陈恬[8]采用两种神经网络对发动机进行气路故障诊断，并利用D-S证据理论进行决策级融合，胡金海[9]等研究了D-S证据理论对3个振动传感器诊断结果的决策级融合。但现有文献中关于D-S证据理论用于故障诊断时，其识别框架一般为故障模式等具体事件，BPA为满足一定形式的具有概率属性的幅值，而燃气涡轮发动机部件性能降级属于表示故障程度的数值，无法直接使用D-S证据理论融合。

基于上述原因，本文提出一种燃气涡轮发动机部件性能降级量化融合方法。通过提取降级计算结果离散序列求取降级分布，使用两种方法实现降级的证据理论描述。最后通过可转移信度模型，将证据理论形式的融合结果还原为概率分布形式，完成降级的多方法计算结果的量化融合。

2 量化融合中的证据理论描述和概率转换方法

2.1 D-S证据理论基本概念

在证据理论中，研究对象的离散取值范围成为识别框架[10]：

识别框架中的元素称为基元。对具体的故障诊断问题，对应于可能出现的故障模式，识别框架对应于所有可能出现的故障模式的并集。

设m1、m2、…、mn是同一识别框架Ω上的n组基本概率分配，焦元分别为 Ai(i=1,2,…,n)，则证据理论规则为：

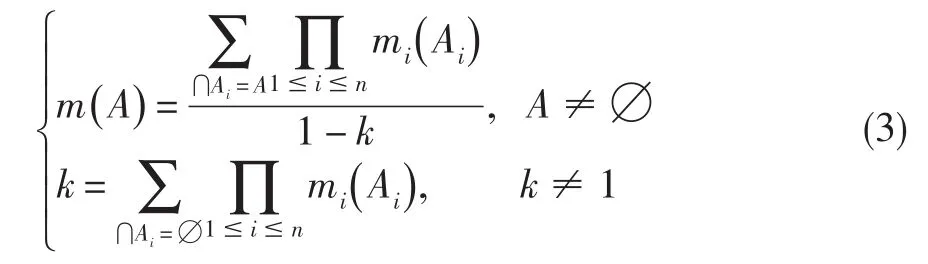
2.2 不确定量的证据理论描述方法

对于有一定测试样本的不确定量，可以通过概率统计方法求取不确定量落在某一区间的概率实现证据理论描述[11-13]。

2.2.1 独立区间划分法

设参数 x测试序列为x1,x2,…,xn，设定其可能性区间为[a,b]，将[a,b]分为k个子区间，记为Ω={ci=[ai,bi],i∈[1,2,…,k]}。对测试样本统计，记样本值属于区间 ci的个数为 qi，i∈[1,2,…,k]。

设识别框架为Θ，其焦元集合为Δi={Ci=(x∈ci)}，则使用数理统计手段得到焦元Ci的BPA为：

2.2.2 嵌套区间划分法

嵌套区间划分法首先设某参数的测试值为x1,x2,…,xn，其均值为：

依据证据理论中mass函数和信任函数(Bel函数)之间的关系，可以构造如下BPA：

2.3 证据理论合成结果的概率描述方法

可传递信度模型(TBM)中给出的Pignistic概率变换，可以将证据理论融合结果转换为概率形式[14]：

研究对象为5台双西门子SINUMERIK 828D系统的数控机床，因此总的监视容量为10套SINUMERIK 828D系统。同时机床监控系统要求系统的实时性强，因此选择了如下方案：整个系统采用C/S架构，采用面向对象的C#软件作为上位界面的开发软件，采用OPC UA通信协议作为系统数据采集以及数控系统与上位机之间的通信协议，选择SQL Server 2008作为服务器上的数据库软件，其他的客户端通过实时访问服务器的数据库实现客户端与服务器之间的数据同步。其主要的功能模块可分为数据采集单元配置、数据采集、数据同步通信、故障报警以及数据分析等，具体如图1所示。

该式是将多命题焦元对应的信度依据均分思想平均分配到各单命题焦元上。

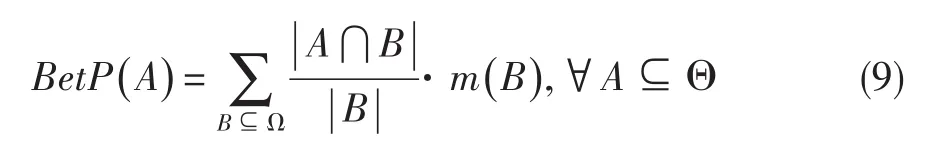
“||”表示命题或焦元的长度，当识别框架中的元素是命题时，则该运算值等于所包含命题的个数。当量化融合时，则运算结果应当是区间长度。采用上述方法可将嵌套区间的mass值分配到独立区间上。

3 压气机效率降级量化融合

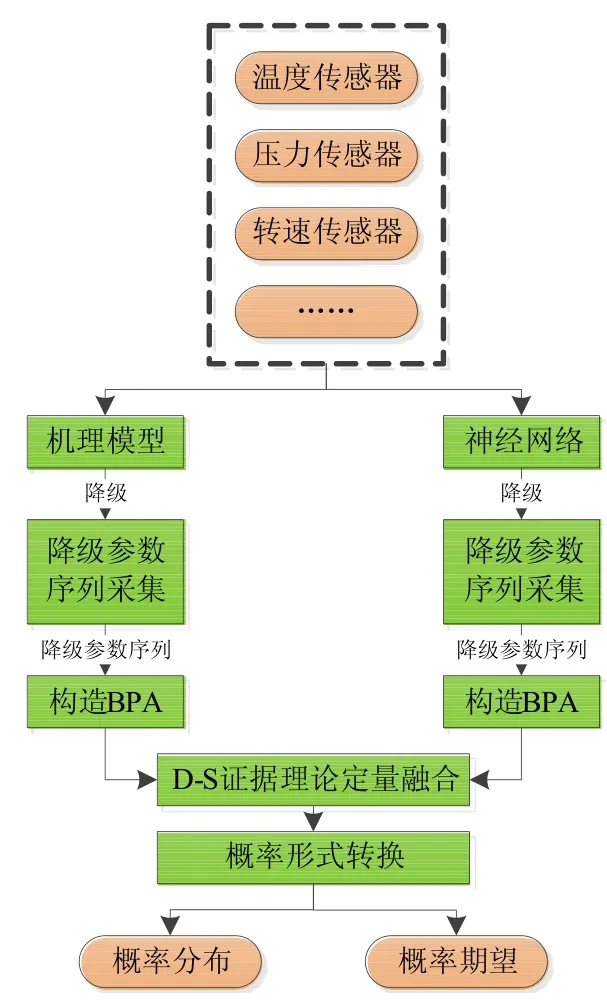
图1 量化融合结构Fig.1 Quantitative fusion architecture

本文构建的量化融合结构如图1所示，建立发动机自适应模型和神经网络模型，并通过发动机运行的传感器数据计算压气机和涡轮的效率降级。采用D-S证据理论对机理模型和神经网络求解的部件性能降级进行量化融合。认为发动机在较短时间内性能变化不大，可选取该时间段内的计算结果作为一组测试序列，通过概率统计方法求取分布，以划分区间的形式构造识别框架与BPA，使用D-S证据理论融合之后将融合结果还原为概率形式。

以压气机效率降级为例，对利用机理模型和神经网络两种降级估计方法计算的732个样本数据采用上述方法构造BPA，并使用D-S证据理论融合。首先采用独立区间划分法(简称方法一)，根据式(4)构造BPA得到m模型和mNN，采用D-S证据理论合成公式对两组证据的BPA合成得到m融合，结果如表1中所示。由于对两组测试样本序列采用了相同的独立区间划分法，因此构造的识别框架是相同的区间，且融合之后的区间划分形式也是相同的独立区间，即为一种概率形式，无需转换。将这种方法构造的BPA和融合结果(m模型、mNN和m融合)以概率统计柱状图的形式表示，如图2所示。从图中可看出，融合之后效率降级在各区间的概率分布更加明显，相同置信度下的置信区间缩小。

表1 方法一得到的BPA和融合结果Table 1 BPA and the fusion results of method one

对利用机理模型和神经网络两种降级估计方法得到的压气机效率降级样本数据采用嵌套区间划分法(简称方法二)。对样本空间从中间向两边逐渐扩大，采用式(7)构造BPA得到如表2所示的基于机理模型方法输出的Bel(Ai)和表3所示的利用神经网络方法输出的Bel(Bi)。可见，此时两种降级估计方法的识别框架不同。

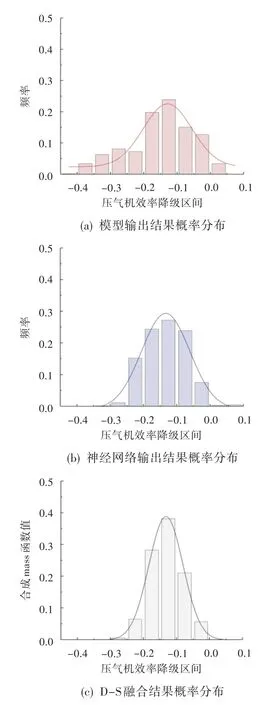
图2 融合前后压气机效率降级概率分布对比(方法一)Fig.2 Comparison of compressor efficiency degradation probability distribution before and after fusion(method one)

表2 方法二得到的BPA(模型输出结果)Table 2 BPA of method two(results of model)

表3 方法二得到的BPA(神经网络输出结果)Table 3 BPA of method two(results of neural network)

采用D-S证据理论合成公式对上述两组证据的BPA进行合成。合成后的区间除两组证据中的区间外，还包含了部分因交集而产生的区间，融合结果仍然是区间存在包含的嵌套形式，如表4所示。

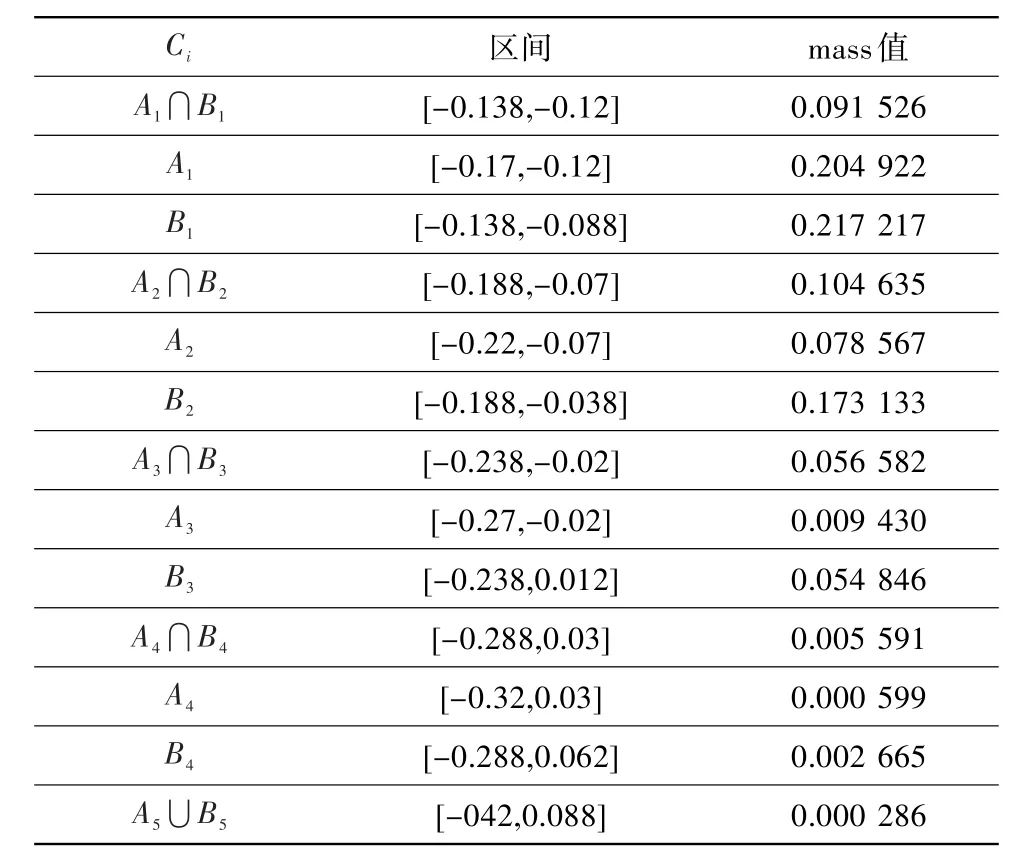
表4 方法二的融合结果Table 4 The fusion results of method two

嵌套区间形式的融合结果虽然可以最大mass值为依据选择其中一个区间作为最终决策结果，但是对于判断降级不够直观。因此，对上述包含嵌套区间的融合结果采用式(9)转换还原为概率形式，还原后的区间由两组BPA的节点共同决定，是互相独立连续的区间划分，结果如表5所示。

图3为方法二得到的两组BPA、融合结果以及还原为独立区间形式的概率分布。从图中可看出，对两组样本分别采用不同的节点划分嵌套区间，融合之后区间会增加，增加的区间依赖于划分节点之间的集合关系。图3(a)和图3(b)中横线越长表示区间越大，按照概率论描述，区间越大则参数落在该区间的概率越大，此时概率值对应于式(6)中的信任函数Bel，由此最大区间必然包含了样本中的所有值。正是由于这种确定性，以式(7)得出的BPA赋予最后一个大区间的mass值最小。从图3(d)可发现，压气机效率降级明显集中在中间三个区间，相对于融合前，对降级的置信区间更小，因此概率分布更集中、融合效果更好。

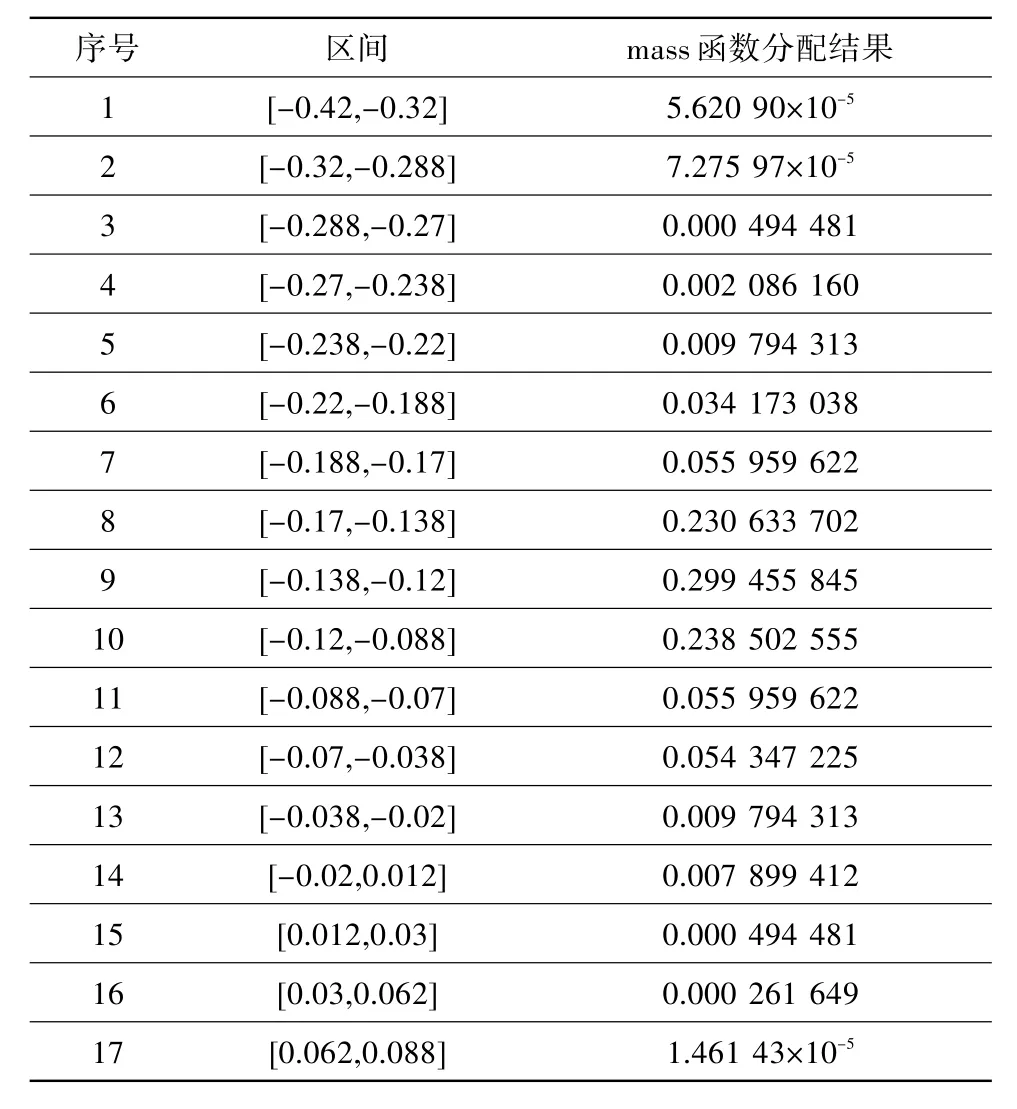
表5 方法二融合结果的概率分布形式Table 5 Probability distribution of method two

对比两种方法的特点，方法一BPA构造方便，合成公式简单，融合结果直观，不需要进一步转换为概率形式即可用于判断降级。但在一些情况如两组测试样本本身的分布均值相差较大时，方法一得到的两组BPA中，分别各有一边存在mass为0的区间，融合结果则只有中间区间有值，此时虽然融合结果集中于中间的区间，但由于证据冲突严重，融合结果可信度会降低。方法二BPA构造较为繁琐，合成公式也相对复杂，融合结果直观性不强，需要进一步还原为概率形式。但融合结果不会出现方法一中仅中间区间有值的现象，信息损失相对较小。由于方法二的区间划分是从均值或中值区间向两侧对称扩展，因此适用于样本为对称分布的情况。

4 结论

针对发动机部件性能降级这一类数值形式无法直接应用D-S证据理论融合的问题，提出两种区间划分方法构造D-S证据理论形式下的BPA。以燃气涡轮发动机压气机效率降级为例，分别采用独立区间划分法和嵌套区间划分法构造BPA，融合性能模

图3 融合前后压气机效率降级概率分布对比(方法二)Fig.3 Comparison of compressor efficiency degradation probability distribution before and after fusion(method two)

型输出结果和神经网络输出结果，并将嵌套区间划分法得到的融合结果还原为概率分布形式。通过研究部件降级的量化融合过程和对比两种BPA构造方法的结果，得出以下结论：

(1)提取较短时间内燃气涡轮发动机部件性能降级的计算结果作为样本，通过区间划分法构造BPA，可实现多方法的降级计算结果的量化融合。

(2)相比于独立区间划分法，嵌套区间划分法构造BPA能够更多地保留融合前的信息，相同置信度下的置信区间更小，融合结果更合理，更适合进行量化融合。

(3)采用多方法计算结果的D-S量化融合，可以提高性能降级参数估计的准确性。

[1]Li Y G.A GPA diagnostic system for aero engine applica⁃tions[J].Journal of Aerospace Power，2007，22(6)：898—908.

[2]Li Y G，Pilidis P.GA-based design-point performance ad⁃aptation and its comparison with ICM-based approach[J].Applied Energy，2010，87(1)：340—348.

[3]张 鹏.基于卡尔曼滤波的航空发动机故障诊断技术研究[D].南京：南京航空航天大学，2008.

[4]翁史烈，王永泓.基于热力参数的燃气轮机智能故障诊断[J].上海交通大学学报，2002，36(2)：165—168.

[5]Banakar A，Sadeghi M，Shushtari A.An intelligent device for diagnosing avian diseases:newcastle,infectious bron⁃chitis,avian influenza[J].Computers&Electronics in Agri⁃culture，2016，127：744—753.

[6]Wen D，Wu X H，Ling D，et al.Application of Demp⁃ster-Shafer evidence theory in fault diagnosis of aero-en⁃gine gas path[C]//.2013 International Conference on Quali⁃ty,Reliability,Risk,Maintenance,and Engineering.2013.

[7]Dewallef P，Romessis C，Léonard O，et al.Combining clas⁃sification techniques with Kalman filters for aircraft en⁃gine diagnostics[J].Journal of Engineering for Gas Tur⁃bines and Power，2006，128(2)：281—287.

[8]陈 恬，孙健国，郝 英.基于神经网络和证据融合理论的航空发动机气路故障诊断[J].航空学报，2006，27(6)：1014—1017.

[9]胡金海，余治国，翟旭升，等.基于改进D-S证据理论的航空发动机转子故障决策融合诊断研究[J].航空学报，2014，35(2)：436—443.

[10]沈怀荣，杨 露，周伟静，等.信息融合故障诊断技术[M].北京：科学出版社，2013.

[11]锁 斌.基于证据理论的不确定性量化方法及其在可靠性工程中的应用研究[R].四川绵阳：中国工程物理研究院，2012.

[12]锁 斌，程永生，曾 超，等.基于D-S理论的靶压幅度不确定性量化方法[J].强激光与粒子束，2011，23(4)：1096—1100.

[13]锁 斌，程永生，曾 超，等.基于证据理论的异类信息统一表示与建模[J].系统仿真学报，2013，25(1)：6—11.

[14]司麦斯.可转移信度模型[M].北京：高等教育出版社，2005.

Quantitative fusion of engine component performance degradation based on D-S evidence theory

WEI Fang1,2，LIANG Mao-zong3，MA Jing-wei1,2，ZHOU Deng-ji3，ZHANG Hui-sheng3
(1.AECC Commercial Aircraft Engine Co.,LTD，Shanghai 201108，China；2.Shanghai Engineering Research Center of Civil Aero Engine，Shanghai 201108，China；3.Gas Turbine Research Institute，Shanghai Jiao Tong University，Shanghai 200240，China)

Aiming at the problem that performance degradation calculated from multiple methods cannot be directly fused byDempster-Shafer(D-S)evidence theory,a method was proposed.The results calculated over a period of time were taken as sample,and the outputs of the performance model and the ANN model were fused.Through building basic probability assignment(BPA)by calculating the frequency in divided in⁃tervals,the quantitative fusion of degradation was realized.After compared the fusion results of two BPA building methods(independent interval method and nested interval method),the main conclusion was drawn that nested interval method was preferable for quantitative fusion.

aero-engine；D-S evidence；performance degradation；BPA；nested interval method；quantitative fusion；information fusion

V231.1+2；TK14

A

1672-2620(2017)04-0011-05

2017-03-13；

2017-06-20

上海市创新行动计划基础研究项目(15JC1404200)

魏 芳(1983-)，女，湖南岳阳人，工程师，硕士，从事发动机健康管理研究。