High Fidelity Simulation of Turbulent Jet and Identification of Acoustic Sources
2017-09-22DonghyukSHINVladAPARECESCUTARIUEdwardRICHARDSON
Dong-hyuk SHIN, Vlad APARECE-SCUTARIU, Edward RICHARDSON
(1. School of Engineering, The University of Edinburgh, Edinburgh, EH9 3DW, United Kingdom;2. Faculty of Engineering and the Environment, The University of Southampton, Southampton, SO17 1BJ, United Kingdom)
High Fidelity Simulation of Turbulent Jet and Identification of Acoustic Sources
Dong-hyuk SHIN1, Vlad APARECE-SCUTARIU1, Edward RICHARDSON2
(1. School of Engineering, The University of Edinburgh, Edinburgh, EH9 3DW, United Kingdom;2. Faculty of Engineering and the Environment, The University of Southampton, Southampton, SO17 1BJ, United Kingdom)
A turbulent round jet at the Reynolds number of 7,290 is simulated by direct numerical simulation to study jet noise source and its propagation. A large domain of 60 diameters in the axial direction, 30 diameters in the radial direction, and full 360 degrees is chosen to minimize the effect of boundary conditions. The spatial statistics of the simulated flow and the peak amplitude of acoustic radiation at 45-degree angle agree well with existing literature, confirming the quality of the data. Motivated by Ffowcs-Williams and Hawkings equation, acoustic source terms for the far-field sound propagation were identified both in the time and the frequency domains. The spectra at three respective locations of the potential core, the shear layer, and the ambient indicate that the fluctuation magnitudes are highest in the shear layer, followed by the potential core and the ambient. The turbulent characteristics are isotropic in the potential core and the shear layer, and the ambient exhibits an intermittent behavior.
jet noise; turbulent jet; self-similarity; Ffowcs-Williams and Hawkings Equation
1 Introduction
Noise is a pressure fluctuation perceived by human ears. Human ears and bodies are quite sensitive to the pressure fluctuations so that even a small of pressure fluctuation can cause people feel very uncomfortable. A good representation is that a loud cheering sound from the entire football stadium is equivalent to a heat energy which can fry one egg. Still, loud noise can cause discomfort at minimum, and health problems at large.
In aviation, aircraft noise is considered as one of pollutions, causing hypertension, hearing impairment, and sleep disorder for the people living near airports. Also, passengers on board also feel uncomfortable with the aircraft noise. As air traffic is expected to grow continuously, there are strong demands and responses to reduce aircraft noise (Dowling and Hynes, 2006).
The noise from aircraft can originate from unsteady flows from aircraft structures including wings, airframes, landing gears, struts, as well as vibrations of panel and engine fans, and engine exhaust gas. One of recent approaches to reduce jet noise is to introduce chevron nozzle at the engine exhaust (Callender et al., 2005). The principal idea of noise reduction by the chevron nozzle is the cancellation due to a phase difference. As the noise is represented by harmonic pressure fluctuation, if two noise sources emit pressure fluctuations out of phase, then the noise in the far field is greatly reduced compared to an in-phase situation. By having saw-tooth shape of chevron nozzle, the noise sources becomes pairs of out of phase. However, by having this complex nozzle, the engine efficiency is reduced by 0.5-1% (Bodony and Lele, 2008). Still, more installation of chevron nozzles indicate the importance of aircraft noise.
As noted, the noise is produced by unsteady flow fields especially turbulent fluctuations of boundary layers, wake regions, and engine exhaust. Turbulent flows are characterized by chaotic flow fields associated with a wide range of time and length scales. This chaotic behaviours are not purely random, but obey a series of conservation equations: conservation of mass, momentum, and energy. Although the governing equations are well formulated and validated for long time, their solutions for practical conditions are challenging and still remain as hot research topics. It is primarily due to the non-linear terms in the governing equations, and they easiliy lead to developments of bifurcations and instabilities.
A well known example of chaotic behaviours is Lorenz system, where Lorenz discovered that a very small difference in initial conditions can lead to a totally different solution at a later time (Lorenz, 1967). This was identified when he conducted numerical simulations of weather prediction on a computer. He conducted presummably two identical simulations—in one simulation, he finished the simulation in one go, and in another “presumably identical” simulation, he finished the simulation half-way, and printed out all the values on a paper, and continued the simulation by typing in the printed values. When he compared the two simulation outputs, he discovered large differences. The cause is a very small truncation error due to the different ways computers and humans recognize numbers—computers uses the base of 2 (binary), while the humans use the base of 10. That small truncation error, which might be in the order of 10-10 causes the deviation in the solution.
2 Characteristics of Turbulent Jet and Acoustics
2.1 Conventional Characteristics of Turbulent Jet
The turbulent round jet is one of the cannonical turbulent flows where the flow is sustained by a momentum source from an inlet surrounded by a quiescent ambient or a co-flow with a lesser momentum. Due to the momentum difference between the inflow and the surrounding, strong shear layers are developed from the edges of the inlet. Then, the acoustics is predominantly produced from the initial development of the shear layers, as the turbulent fluctuations are strongest in this region. Further downstream, the shear layers start to merge together, developing a self-similar region of the turbulent jet. Before the merge of the shear layers and near the centreline, there is a conical region unaffected by the shear layer, called potential core. In the potential core, the flow maintains the same characteristics of the inflow conditions.
In the self-similar region, all flow properties can be simplified to reduced independent variables. If a flow variable is scaled by the centreline velocity, the profiles at different locations collapse into a single curve with respect to a scaled radius. The scaled radius is typically the ratio of the radial coordinate to the axial coordinate, i.e.,r/(x-x0) including the virtual origin,x0. The mean axial velocity field is quite similar to the Guassian profile, and the mean radial profile can be calculated from the mean axial velocity profile through the mass continuity equation. In the self-similar region, the turbulent fluctuation is around 20% of the mean axial velocity at the centreline, and decays away from the centerline (Pope, 2000).
2.2 Ffowcs-Williams and Hawkings Equation
The noise, represented by a pressure fluctuation, is a small vibration compared to the mean atmospheric pressure. For example, an extremely unpleasant noise level of 100 dB, equivalent to hearing a fighter jet at 300 m, is caused by a pressure fluctuation of 2 Pa. Compared to the atmospheric pressure, this pressure fluctuation is less than 0.002% of 101,325 Pa. Because of this small magnitude, the noise propagation can be understood by linearized versions of flow equations.
Although the noise propagation is relatively simple, the noise sources in turbulent flows are not as simple. Ffowcs-Williams and Hawkings (1969) have formulated the pressure popagation from a volume of sound sources. The so-called Ffowcs-Williams and Hawkings equation is written as:
(1)
where
(2)
(3)
whereviis theithvelocity component,τijis the viscous shear stress,δijis the Kroneckerδ-function. Lyu et al. (2017) states that when the Reynolds number is high, which is of practical situations, the viscous terms inTijcan be neglected (Lighthill 1952; Goldstein 2003; Karabasov et al. 2010). Also, when the temperature difference between the jet and the ambient is small, which is a good approximation for cold jets at low Mach numbers, the pressure fluctuations is considered to be balanced out by the product of the density fluctuations (Lighthill, 1952).
3 Simulation of Turbulent Round Jet
The simulated flow is a canonical turbulent round jet, a stream of momentum source emitted into a stagnant ambient fluid. A representative flow field is depicted in Figure 1, where an instantaneous axial velocity field are shown in a middle plane. The turbulent jet is sustained by an injected flow at a bulk speed ofU0from the round inlet of a diameter,Dto the stagnant ambient. The injected flow has the same transport properties as the ambient, and all fluids obey the perfect gas law. The jet Reynolds numberReD=(U0D)/vis 7,290, wherevis the kinematic viscosity, and the Mach number is 0.304, based on the bulk velocityU0.
The inlet plane consists of the jet inlet surrounded by a wall boundary. Inside the jet inlet, the mean axial velocity is prescribed as a smoothened top-hat profile—the mean values are constant from the centerline to a radius ofr=0.475D, and drop smoothly to zero atr=0.5Dusing a half cosine function. Away from the jet inlet (r>0.5D), the wall boundary condition is imposed with the no-slip condition. For the fluctuating part at the jet inlet, pseudo-turbulent homogeneous isotropic velocity fluctuations are superimposed with a low turbulence intensity of 3% using the digital filter method (Touber et al., 2009).
All the other boundaries are non-reflecting outlets (Poinsot and Lele, 1992) with a small buffer region (Sandberg et al., 2006) at the downstream outlet boundary. In the buffer region, the viscosity is artificially increased to minimize spurious acoustic reflection from the boundaries. For transport properties, all scalar diffusivities are set by the assuming Lewis numbers equal to unity, and a Prandtl number equal to 0.72. Viscosity changes with temperature following Sutherland’s Law (Sutherland et al., 1893).
The simulation is conducted with the compressible DNS code, HiPSTAR, developed at the University of Southampton. The code is designed for high performance computing, and shows good scaling up to 10,000 cores. The code is recently used for turbulent boundary layer study (Bechlars and Sandberg, 2017). A fourth-order central finite difference scheme with energy conserving boundary schemes of same order (Nordstroem et al., 1999) are used in the longitudinal and the radial directions, while a pseudo-spectral method is used in the circumferential direction. The singularity of the axis resulting from the cylindrical coordinate system is treated using parity conditions (Sandberg et al., 2011). A fourth-order low-memory Runge-Kutta scheme (Kennedy et al., 2000) is used for time advancement. In addition, skew-symmetric splitting of the nonlinear terms is used to enhance the stability (Kennedy et al., 2008).
For the computational mesh, a stretched grid is used, modified from a previous round jet study (Sandberg et al., 2012). The original grid spacingΔwas scaled using the Kolmogorov scaling (Δ~ReD3/4). In the radial direction, the grid is most refined near theΔdge of the jet inlet (r=D/2) where flow gradients are the greatest, and 145 points are radially assigned within the jet diameter. In the axial direction, the grid is most refined near the inlet and gradually stretched away from the inlet. In the circumferential direction, 64 Fourier modes are used, which is equivalent to have 130 physical collocation points. The grid consists of 3020×834×130 structured nodes, spanning axially fromx=0-60Dand radially fromr=0-30D.
In order to speed up the development of the statistically-converged jet flow field, the initial simulation was conducted using a computational mesh with a half-resolved grid of the final grid for 540 jet times (τ=D/U0). By the 540 jet times, it was observed that the first and second order statistics have reached the statistically-stationary states. Then, the coarse-grid solutions are interpolated onto the final grid, and the simulation continued over an additional 80τ, confirming that statistical-stationarity is re-established. Subsequently, statistics are sampled over 380 jet times. The converged turbulent jet simulation also displays self-similarity downstream of 40 diameters.
4 Simulation Result and Discussion
In this section, the mean and fluctuating flow fields are presented and analyzed from the simulated turbulent jets. The radial profiles of mean and fluctuating velocity components agree well with other existing measurements. Furthermore, the temporal and spectral statistics of the flow fluctuations, which are relevant to acoustic source, are analyzed. Figure 2 shows a dilation field, an effective density fluctuation, of the turbulent jet on a middle plane. Spherical waves propagating from the jet inlet illustrate the acoustic sources are clustered around the shear layer near the inlet. The peak amplitude in the 45-degree angle agrees with existing literature (Bodony and Lele, 2008).
Figure 3 shows the axial evolution of the centerline mean and fluctuating velocities. Close to the inlet, the mean velocity remains constant because the regime is within the potential core. Downstream of the potential core, the mean velocity decays proportional to 1/x. The proportionality of the decay is known to differ by inlet conditions and boundary condition. The decay proportionality of our simulation is 6.7, which is within the reported ranges of 5.5 to 7.5. The turbulent intensity in the solid blue line shows the peak occurs nearx/D=7 and decays subsequently with 1/x. The same 1/x-dependency agrees well with the known characteristics of self-similar turbulent jets.
Figure 4 shows the first and second moments of the axial and radial velocity components from the simulation versus the scaled radius (η=r/(x-x0)), wherex0is a virtual origin. The experiment of Panchapakesan et al. (1993) was chosen for the comparison because they used the same boundary condition as the present DNS involving a near-laminar jet with a top hat velocity profile issuing from a converging nozzle. All the mean quantities of the current simulation show adequate agreement with the laboratory measurements. Panchapakesan et al. (1993) reported that the higher moments reach a self-similar state at aroundx/D=70. It was noted that the statistics achieved self-similarity already afterx/D=15 for the first moment, andx/D=25 for the second moment, and note that this might be attributable to the lower Reynolds number of the DNS, since the jet Reynolds number is 11,000 in the measurements reported by (Panchapakesan et al., 1993).
In incompressible flows, the mean radial velocity of self-similar turbulent round jet can be derived from the mean axial velocity profiles by the following formula:
(4)
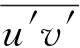
(5)
Figure 5 shows the temporal profiles of flow field at selected locations. The selected locations are at a fixedx-location (x/D=5) and three radial locations. The radial locations are chosen to be in the potential core (r/D=0), the shear layer (r/D=0.5), and the ambient (r/D=1.25). Overall, the fluctuation magnitude is highest in the shear layer, and the ambient exhibits some levels of intermittency-constant changes between turbulent and laminar regimes. Inside the potential core, the fluctuation is not completely zero-also note that 3% synthetic fluctuations are imposed at the inlet boundary condition.
The axial velocities shown in Figure 5a clearly demonstrate a separation of mean values by the radial locations. At the shear layer, the mean value drops to almost a half of the value in the potential core. In the ambient, the velocity is almost zero, but remains positive. The positive velocity in the ambient is related with entrainment, a process by which the ambient is entrapped into the jet.
All the radial velocities shown in Figure 5b fluctuate around zero. The mean values are slightly lower than zero, and the fluctuating components are much higher than the mean values. The fluctuation magnitudes are similar in both potential core and the shear layer, and the ambient exhibits very low level of fluctuations.
For both density and pressure fluctuations, they show a low frequency modulation. This low frequency modulation is due to small reflections of acoustic waves from boundaries. Although additional sponge layers are added near the boundaries, small artificial acoustic waves still reflect back to the internal domain. As the fluctuation magnitudes of density and pressure are much smaller than the means, the modulations are more visible than the velocity signals.
Figure 6 shows the spectra of the flow components of axial velocity, radial velocity, density, and pressure at the selected locations over the non-dimensional frequency, Strouhal number (St=f·D/U0). The selected locations are identical to the ones shown in Figure 5.
The spectra of the axial velocity in Figure 6a show that overall the fluctuation intensities are highest in the shear layer at all frequencies compared to the potential core and the ambient. In low frequencies (St<0.8), the values of the ambient are higher than those of the potential core. This may be related to an entrainment process in the ambient, which is a large length-scale process. In addition, the intermittency behavior in the ambient would contribute more to the low frequency response. In high frequencies, the values of the potential core are much higher than the ambient, which is consistent with the higher turbulent intensity inside the potential core.
In Figure 6a, best-fitted power-law lines are added for the high frequencies. For the shear layer and the potential cores,St-5/3was the best fitting power-law curve, whileSt-10/3for the ambient. TheSt-5/3scaling indicates that the corresponding regions (the shear layer and the potential core) are locally isotropic, while the ambient is not.
The spectra of the radial velocity show the similar trends as the axial velocity: (i) the values are highest in the shear layer at all frequencies; (ii) in low frequencies, the magnitudes of the ambient are higher than the potential core, but opposite in high frequencies; (iii) the fitted power-law curves are different in each regime, indicating the flows are locally isotropic in the shear layer and the potential core, but not in the ambient.
Next, the spectra of the density are slightly different from the velocity spectra. Overall, the magnitudes in the shear layer and the potential cores are comparable at all frequencies. In low frequencies, the magnitudes in the ambient are the highest, but decrease faster at high frequencies. At high frequencies, the fitted power-law curves areSt-5/6for the shear layer and the potential core andSt-3/5for the ambient. Each of the power exponents are a half of the velocities, respectively. As the density and the velocities are directly related by the mass conservation equation, the half exponent can be the artifact of the equation.
For the spectra of the pressure, the magnitudes show the clear separation among each regime. The magnitudes of the shear layer are highest at all frequencies, and those of the ambient are lowest. Interestingly, the fitted power-law curves have the same power exponent at all regimes,St-5/6. As the fluid obeys the perfect gas law (ρ=pRT), this indicates that spectra of temperature will can be deduced. However, as the magnitude of pressure is much higher than the magnitude of density, it is possible that the temperature spectrum can follow the same spectrum of pressure, i.e.,St-5/3for all regimes.
5 Conclusion
A turbulent round jet is simulated with direct numerical simulation. The simulation results are validated against the data from literature, and show good agreement. Motivated by Ffowcs-Williams and Hawkings equation, acoustic source terms for the far-field sound propagation were identified both in the time and the frequency domains. The spectra at three respective locations of potential core, shear layer, and the ambient indicate that the fluctuation magnitudes are highest in the shear layer, followed by the potential core and the ambient. The turbulent characteristics are isotropic in the potential core and the shear layer, and the ambient exhibits an intermittent behavior.
Reference
[1] Bechlars, P., and R. D. Sandberg. “Variation of enstrophy production and strain rotation relation in a turbulent boundary layer.” Journal of Fluid Mechanics 812 (2017): 321-348.
[2] Bodony, Daniel J., and Sanjiva K. Lele. “Current status of jet noise predictions using large-eddy simulation.” AIAA journal 46.2 (2008): 364.
[3] Callender, Bryan, Ephraim Gutmark, and Steve Martens. “Far-field acoustic investigation into chevron nozzle mechanisms and trends.” AIAA J 43.1 (2005): 87-95.
[4] Carpenter, Mark H., Jan Nordstr?m, and David Gottlieb. “A stable and conservative interface treatment of arbitrary spatial accuracy.” Journal of Computational Physics 148.2 (1999): 341-365.
[5] Dowling, A. P., and Tom Hynes. “Towards a silent aircraft.” The Aeronautical Journal 110.1110 (2006): 487-494.
[6] Goldstein, Marvin E. “A generalized acoustic analogy.” Journal of Fluid Mechanics, 488 (2003): 315-333.
[7] Karabasov, S. A. “Understanding jet noise.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 368.1924 (2010): 3593-3608.
[8] Kennedy, Christopher A., and Andrea Gruber. “Reduced aliasing formulations of the convective terms within the Navier-Stokes equations for a compressible fluid.” Journal of Computational Physics 227.3 (2008): 1676-1700.
[9] Kennedy, Christopher A., Mark H. Carpenter, and R. Michael Lewis. “Low-storage, explicit Runge-Kutta schemes for the compressible Navier-Stokes equations.” Applied numerical mathematics 35.3 (2000): 177-219.
[10] Lighthill, M. J. “On sound generated aerodynamically I. General theory.” Proc. R. Soc. Lond. A, 211 (1952): 564-587.
[11] Lorenz, Edward N. “The Nature and Theory of the General Circulation of the Atmosphere.” Geneva: World Meteorological Organization. (1967).
[12] Lyu, B., A. P. Dowling, and I. Naqavi. “Prediction of installed jet noise.” Journal of Fluid Mechanics, 811 (2017): 234-268.
[13] Panchapakesan, N. R., and J. L. Lumley. “Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet.” Journal of Fluid Mechanics 246 (1993): 197-223.
[14] Poinsot, T., and S. K. Lele. “Boundary conditions for subsonic Navier-Stokes calculations.” J. Comp. Phys 101 (1992): 104-129.
[15] Pope, Stephen B. “Turbulent flows.” (2001): 2020.
[16] Sandberg, Richard D. “An axis treatment for flow equations in cylindrical coordinates based on parity conditions.” Computers & Fluids 49.1 (2011): 166-172.
[17] Sandberg, Richard D., and Neil D. Sandham. “Nonreflecting zonal characteristic boundary condition for direct numerical simulation of aerodynamic sound.” AIAA journal 44.2 (2006): 402-405.
[18] Sandberg, Richard D., Neil D. Sandham, and Victoria Suponitsky. “DNS of compressible pipe flow exiting into a coflow.” International Journal of Heat and Fluid Flow 35 (2012): 33-44.
[19] Sutherland, William. “LII. The viscosity of gases and molecular force.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 36.223 (1893): 507-531.
[20] Touber, Emile, and Neil D. Sandham. “Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble.” Theoretical and Computational Fluid Dynamics 23.2 (2009): 79-107.
[21] Williams, J. F., and Hawkings, D. L. (1969). “Sound generation by turbulence and surfaces in arbitrary motion.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 264(1151), 321-342.
10.19416/j.cnki.1674-9804.2017.03.001
