温控射频消融温度场仿真模型参数敏感性分析

王笑茹，高宏建，吴水才，白燕萍

北京工业大学 生命科学与生物工程学院，北京 100124

温控射频消融温度场仿真模型参数敏感性分析

王笑茹，高宏建，吴水才，白燕萍

北京工业大学 生命科学与生物工程学院，北京 100124

目的研究温控射频消融温度场仿真模型中特性参数的敏感性，分析特性参数对于消融区温度分布的影响。方法利用有限元技术建立温度场仿真模型，基于方差分析理论研究基本特性参数变化对于消融区尺寸和不同点温度的方差贡献率（SS%）和主效应。结果研究表明，在近场区域中，消融前期电导率（Sigma）和组织等效电阻（R）的SS%约为22%，消融后期SS%约为47.5%；在远场区域中，消融前期Sigma和R的SS%约为26%，消融后期SS%约为43%；对于消融区尺寸而言，消融前期Sigma和R的SS%约为36%，消融后期SS%约为42%；根据主效应分析，参数Sigma和R与温度成正相关，比热容和密度与温度成负相关，导热率与温度的相关性随时间和位置而有所变化。结论在射频热消融过程中，相比于导热率、密度、比热容和介电常数，电导率和组织等效电阻具有显著敏感性。

射频消融；温度场仿真；模型参数；敏感性分析

引言

射频热消融（Radiofrequency Ablation，RFA）技术是将交流电场施加到肿瘤组织，通过电阻加热提升靶组织的温度，使之产生凝固性坏死，从而实现对肿瘤的原位灭活[1]。该技术因具有微创、治疗效果显著等优点而在肝肿瘤治疗中得到了广泛应用，但热消融的质量仍取决于临床医生的经验。研究表明[2-4]，热消融效果主要取决于消融区的范围、形状及其内部的温度场分布。因此，热消融温度场的精确表征显得尤为重要。

计算机建模仿真技术不仅能够观测消融区温度变化，还有助于医生术前制定合理手术计划。张曼[5]基于Pennes和Hyperbolic传热方程，讨论了不同传热模型对于温度场的影响。聂晓慧[6]研究了脊柱肿瘤射频消融适形治疗的温度场。Jin等[7]建立了基于MRI的甲状腺射频消融有限元模型。但这些文献中将温度场模型中的热参数和电参数取为固定值，未考虑生物组织热物性参数的特异性变化，从而使得消融结果存在较大的误差。黄维等[8]基于反馈温度的比例积分控制方法调节电极针施加电压，构建温控射频消融仿真模型，但未涉及特性参数对于中心电压的影响。针对上述问题，可通过温度反馈来调节组织参数，减少仿真误差。由于温度场仿真模型中具有多个特性参数，因此反馈调节需要重点关注对误差影响显著的因素，即敏感性参数。为了解决这一问题，本文通过方差分析对温度场模型中的特性参数进行敏感性分析，获得对模型具有显著性影响的参数，由此为特性参数的精确表征和温度场的反馈调节提供科学依据。

敏感性分析是一种定量描述输入参数对输出响应程度的方法[9]，其量化指标为误差的方差贡献率。方差贡献率越大，则参数对模型响应的影响也就越大[10]。本研究的目的在于通过敏感性分析，获得各特性参数的影响显著性，在反馈应用中去除敏感性较低的参数，重点考虑敏感性较高的参数，由此有效地降低模型的复杂度，减少数据运算，进一步提高仿真模型的精度。

在临床射频热消融手术中，常用的是温控射频消融仪，其根据所设置的参数（中心温度、温升速率等）实时地调节输出功率，通过功率补偿获得恒定的中心温度，最终获得所需的热凝固效果。本研究基于恒温热消融仪RFA-I（Blade Co.，Ltd.，Beijing，China）和仿肝组织体模建立温控射频热消融温度场模型，建模软件为COMSOL Multiphysics软件（COMSOL Inc.，Palo Alto，CA，USA）；然后利用Minitab（State College，PA，USA）中的因子分析来研究各特性参数的敏感性，为后续反馈工作提供可靠依据。

1 热消融温度场的建模

热消融仿真模型的构建主要基于电磁技术和生物传热技术，通过电磁技术获得各个点的热源，并且通过生物传热技术获得各个点的温度分布。

1.1 电磁源和生物传热建模

在射频消融仿真过程中，电流场作为热源，是焦耳热产生的主要原因，其控制方程为拉普拉斯方程(1)～(3)：

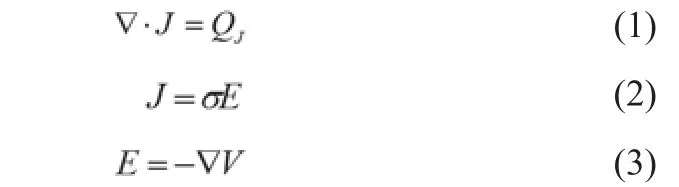
其中J表示电功，σ表示电导率，E表示电场强度，V表示电压源，由功率公式可知：

其中R（单位：Ω）为组织的等效电阻值，P（单位：W）根据实验中的温控射频消融仪获得，在本研究中为时间的函数：

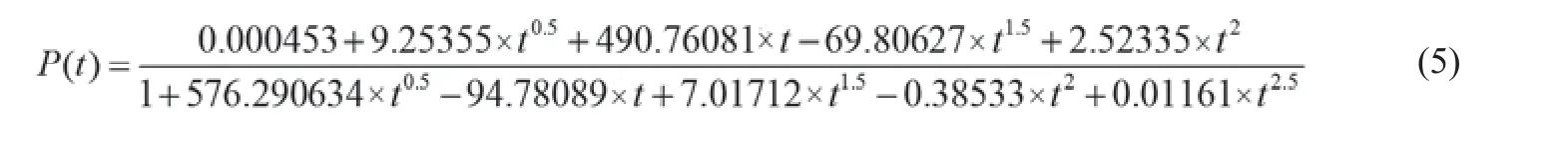
本研究中采用的生物传热方程为经典的Pennes生物传热方程（PBE），具体描述如下：

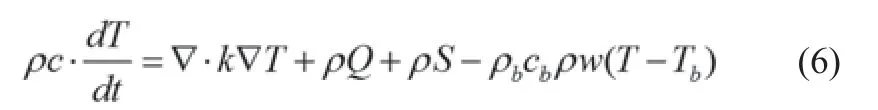
其中T为温度（℃），t为时间（s），ρ为体积质量密度（kg/m3），c为比热容（J/kg·℃），k为导热率[J/(s·m·℃)]，w为体积血液灌注率[kg/(m3·s)]，Q为代谢热生成速率[J/(m3·s)]，S为比吸收率SAR（W/kg），下标b表示组织的血液特性。

1.2 基于有限元技术的温度场模型求解

模型的建立和求解在COMSOL Multiphysics软件中完成，其中采用的技术为有限元方法（Finite Element Methods，FEM），其通过计算机采用分片近似，逼近整体的研究思想来求解物理问题[11]。本文采用基于多极射频电极的温控射频消融温度场模型，该模型的尺寸与实验体模（50 mm×50 mm×70 mm）的尺寸相同。考虑到射频电极分布的对称性，并且为了减少仿真计算时间，仅建立1/2几何模型，大小为50 mm×25 mm×70 mm，见图1。多极射频电极形状，见图2。电极周围的长方体为仿肝组织，6个子电极均匀分布在几何模型的一侧，两个子电极间的夹角为55°，每个子电极的挠曲度不同，相邻两个子电极的挠曲度为104°和57°。

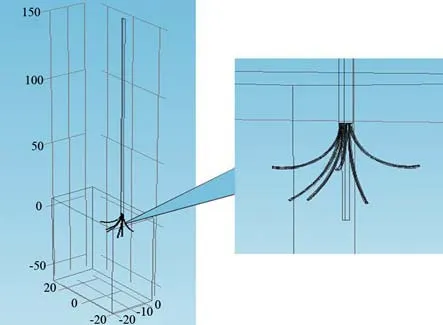
图1 多极射频消融温度场仿真的几何模型

图2 多极射频消融电极的实际模型

为了得到有限元模型的定解，设定仿真模型的边界条件和初始条件。对于电流场，多极射频电极的边界设定为热源，肝组织边界设定为地电极，电势为0 V；对于生物传热物理场，模型初始温度为28℃，模型外部热边界条件为28℃；模型加热时间为360 s；忽略组织血液灌注率w对仿真温度的影响。

2 特性参数的敏感性分析

为研究热物性参数和电特性参数对热消融温度场的影响，利用Minitab软件设计32组仿真实验，具体设置见表1。其中各参数的取值范围源自已有报道[12-13]，见表2。为了研究特性参数对温度分布的影响，选取包括远场点（1.5 cm，0 cm）和近场点（0.5 cm，0 cm）的多个点以及消融区等温面进行敏感性分析。

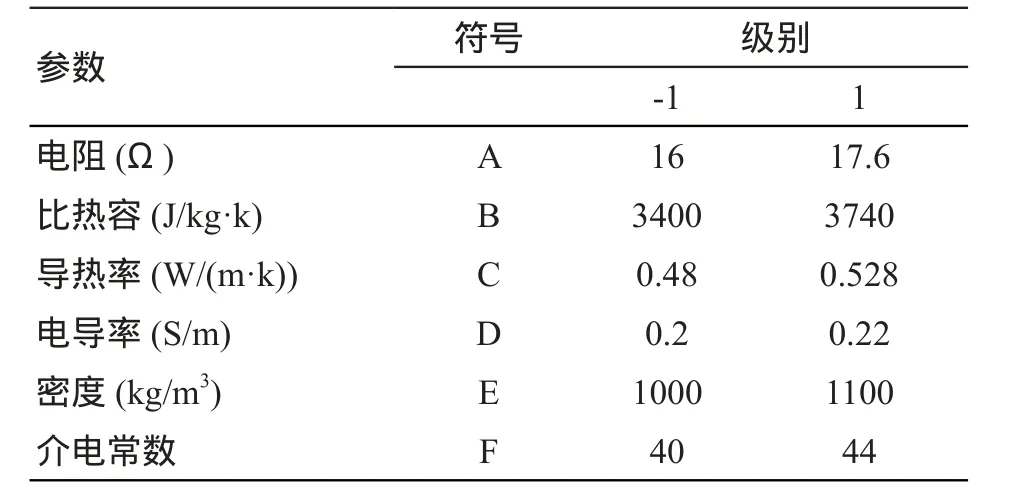
表1 特性参数和取值范围

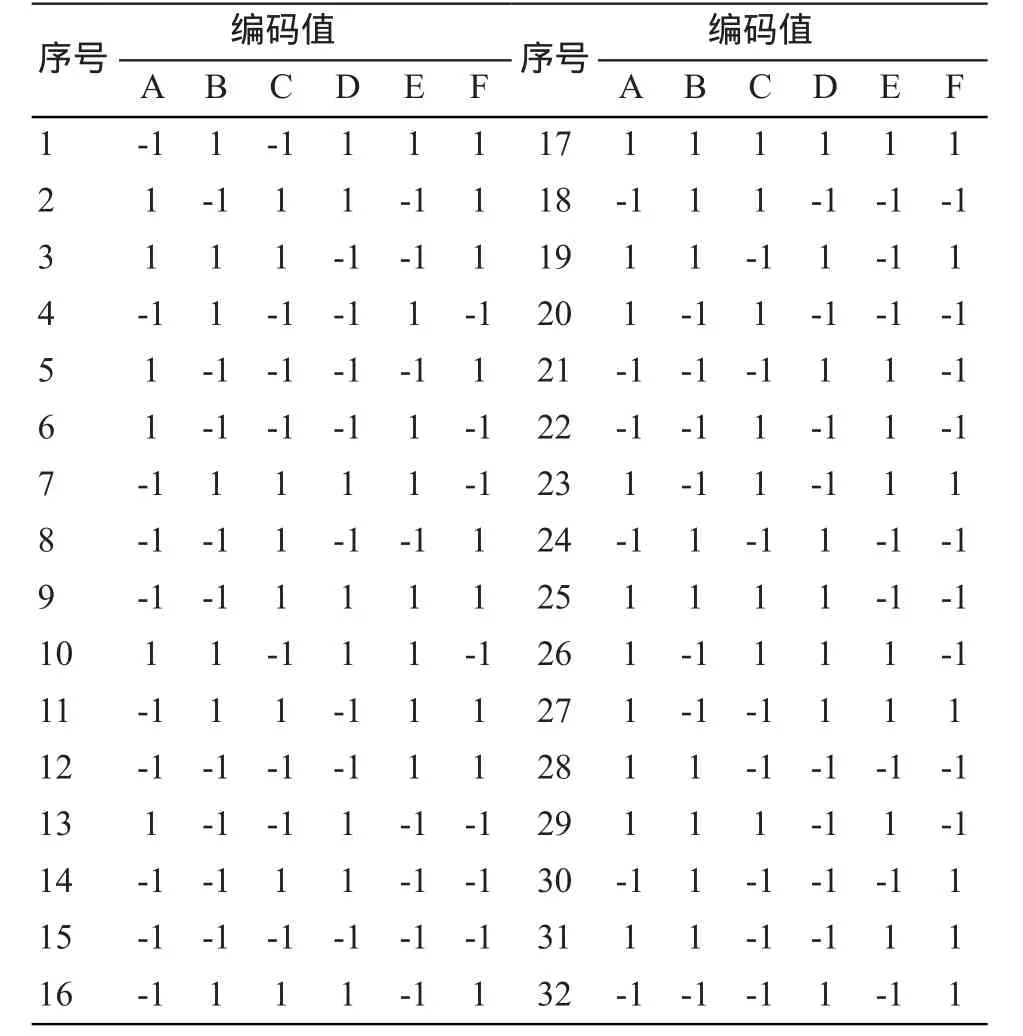
表2 方差分析的32实验安排

2.1 远场点参数敏感性分析

根据表2中的32组实验安排，分别在Comsol软件中进行温度场模型仿真，每组实验消融时间为360 s。参数R、Cp、k、Sigma、rho和Epsilon在t=50 s和t=360 s时对远场点的主效应图，见图3。该主效应图反映了各参数对消融温度的影响趋势。各参数在整个仿真过程中远场点方差贡献率的趋势图，见图4，其中Cp和rho变化趋势相同，在图中重合；R和Sigma的变化趋势十分相似。由图3和图4可知，随着仿真时间的增加，Cp和rho对远场点消融温度的影响越来越小，且呈负相关；k对远场点消融温度的影响一直很弱；R和Sigma对远场点消融温度的影响一直很大，为显著性影响因素；Epsilon对消融温度结果无影响。

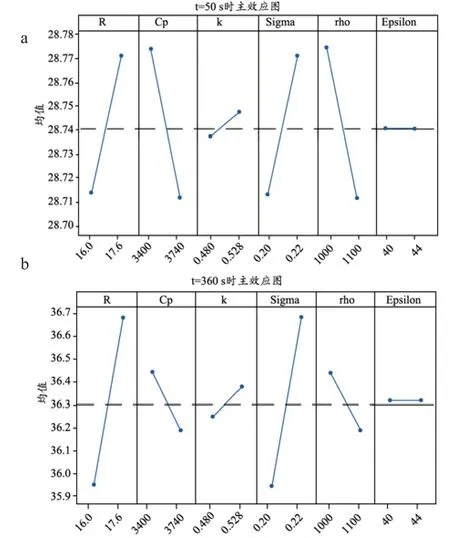
图3 各参数在t=50 s（a）和t=360 s（b）时对远场点温度的主效应图

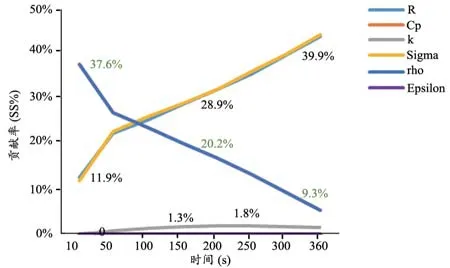
图4 仿真过程中各参数对远场点方差贡献率趋势图

为了得到各参数对消融温度场影响的定量分析，进一步对各组实验结果进行方差分析，结果见表3。F值是衡量数据均值的方差，该值越大则参数影响越显著；P值为用于判定假设检验结果的参数[9]，根据方差分析，P值＜0.05说明该参数具有显著性；Adj_SS(SS)表示参数的方差和；Adj_MS(MS)表示参数方差的平均值；贡献率SS%表示方差偏离均值的平方和，其大小可定量地反应各参数对消融温度场的影响显著性，如公式(7)所示：

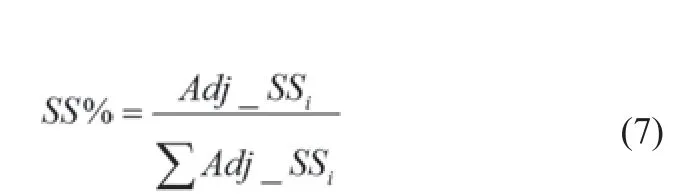
式中，i取A、B、C、D、E和F；Adj_SSi表示参数i的方差和。

表3中的SS%结果和图4的趋势图表明，消融前期各参数敏感性为：Cp（rho）＞Sigma＞R＞k＞两因子交互作用＞Epsilon（Epsilon=0，故表3中未列出）；在消融后期各参数的敏感性为：Sigma＞R＞Cp（rho）＞k＞两因子交互作用＞Epsilon；其中Epsilon对消融温度始终没有影响，因此在后续分析中可忽略参数Epsilon。

为了直观地观测对温度场影响显著的参数Sigma和R之间的交互作用，进一步绘制出不同参数和消融温度结果的等值线图，该等值线图反映了两个参数变量和响应之间的关系，见图5。该图表示Sigma和R同时增大时，消融温度会略有增加，如图5中右上角区域所示。另外结合因子交互作用的SS%值（＜0.2%），可忽略不计参数间交互作用对消融区的影响。

2.2 近场点参数敏感性分析

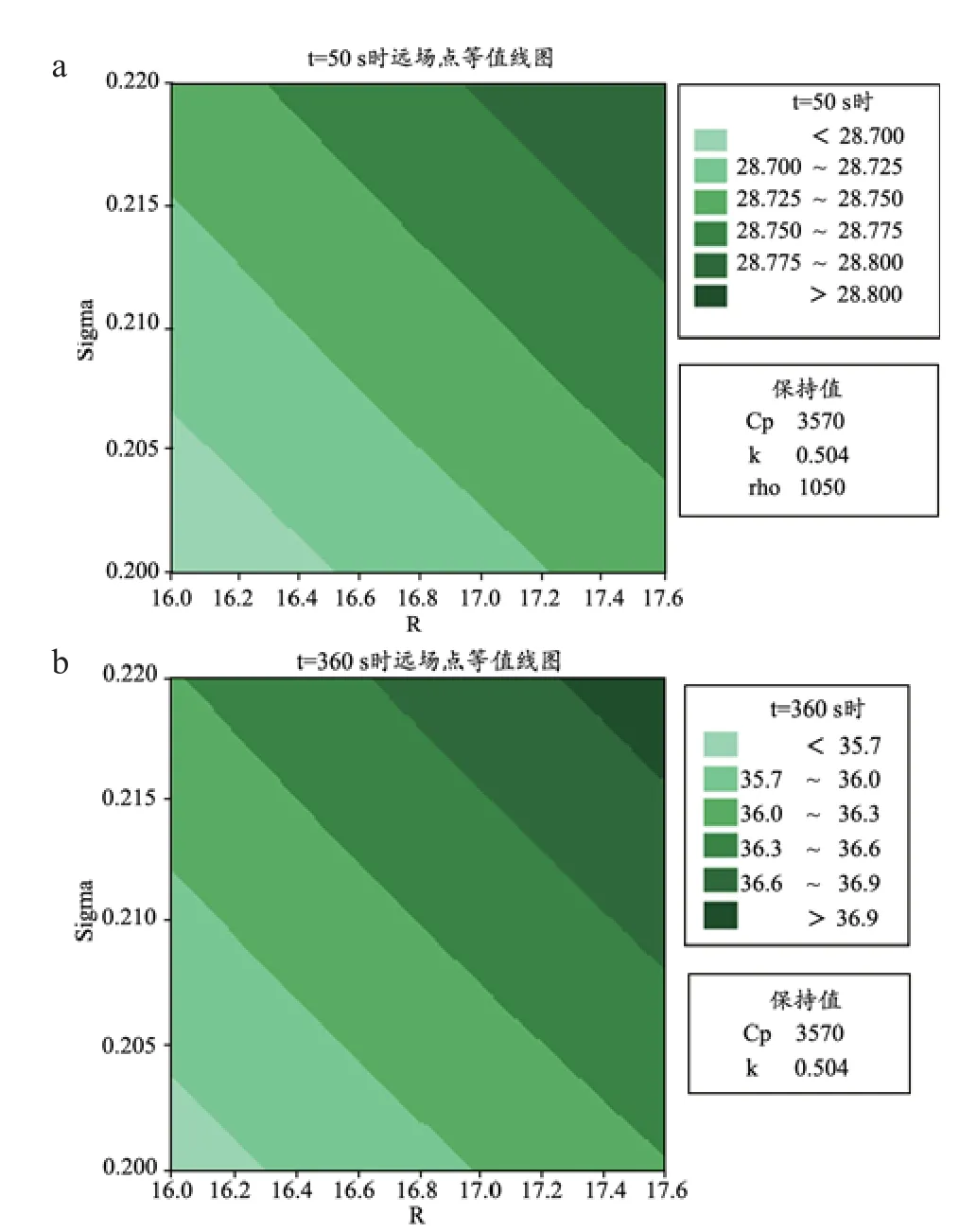
图5 Sigma和R在t=50 s（a）和t=360 s（b）的远场等温线图

表3 t=50 s以及t=360 s 时的远场点方差分析

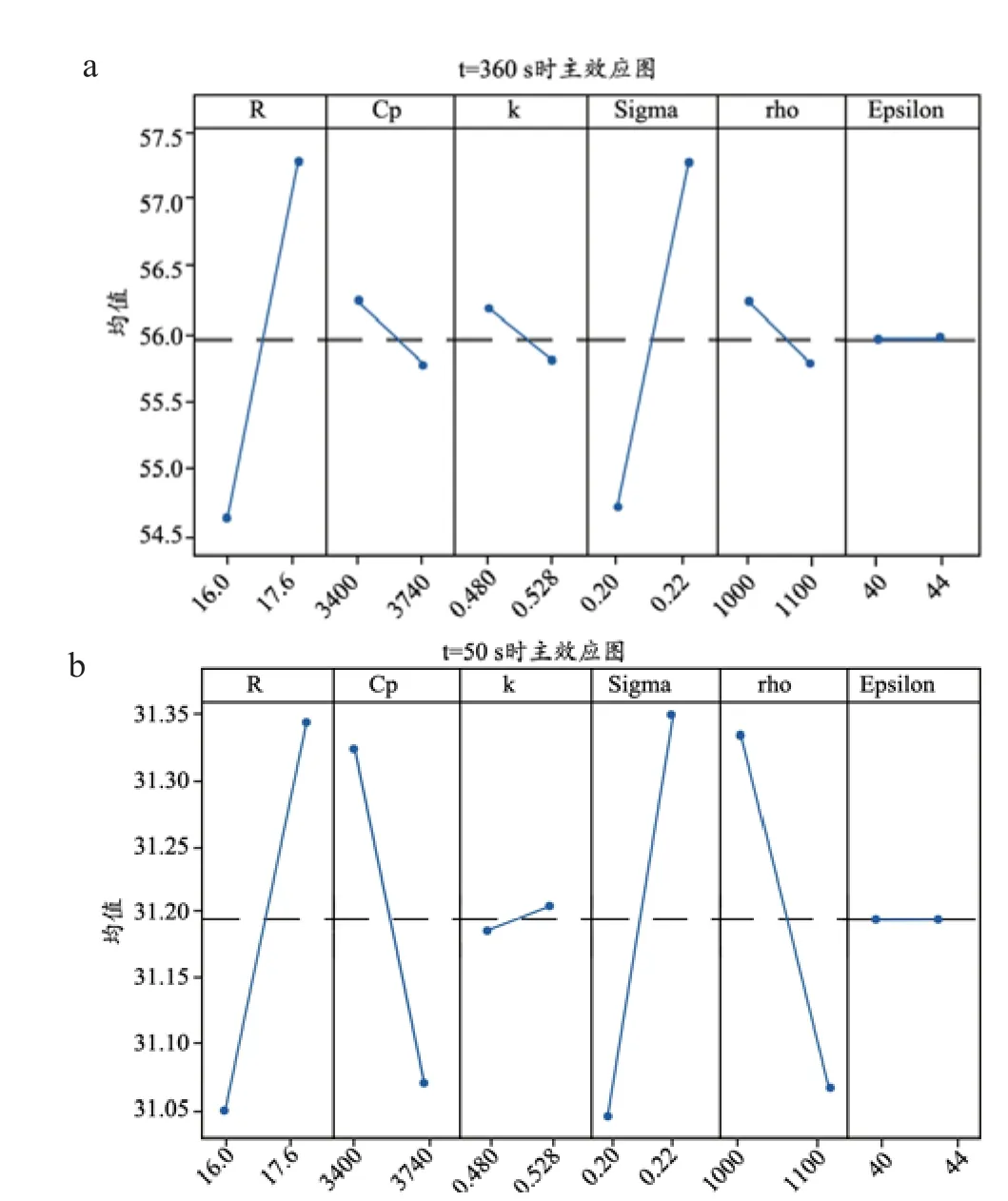
图6 各参数在t=50 s（a）和t=360 s（b）时对近场点温度的主效应图

图7 仿真过程中各参数对近场点方差贡献率趋势图

该分析采用与远场点参数敏感性分析相同的模型仿真条件。参数R、Cp、k、Sigma、rho和Epsilon在t=50 s、和t=360 s时对近场点的主效应图，见图6。各参数在整个仿真过程中近场点方差贡献率的趋势图，见图7，其中Cp和rho变化趋势相同，在图中重合；R和Sigma的变化趋势十分相似。由图6和图7可知，随着仿真时间的增加，Cp和rho对近场点消融温度的影响越来越小，呈负相关；k对近场点消融温度的影响一直很弱；R和Sigma对远场点消融温度的影响一直很大，为显著性影响因素；Epsilon对近场点温度始终无影响。

t=50 s以及t=360 s时的近场点方差分析结果，见表4。表4中的SS%结果和图7的趋势图表明，消融前期各参数的敏感性大小为：Cp（rho）＞Sigma＞R＞k＞交互作用＞Epsilon；消融后期各参数的敏感性为：Sigma＞R＞Cp（rho）＞k＞交互作用＞Epsilon。

参数Sigma和R的交互作用对消融温度的影响，见图8。随着Sigma和R的增大近场点消融温度升高，如图中右上角区域所示。结合因子交互作用的SS%值（＜0.2%），故可忽略不计参数间交互作用对消融区的影响。

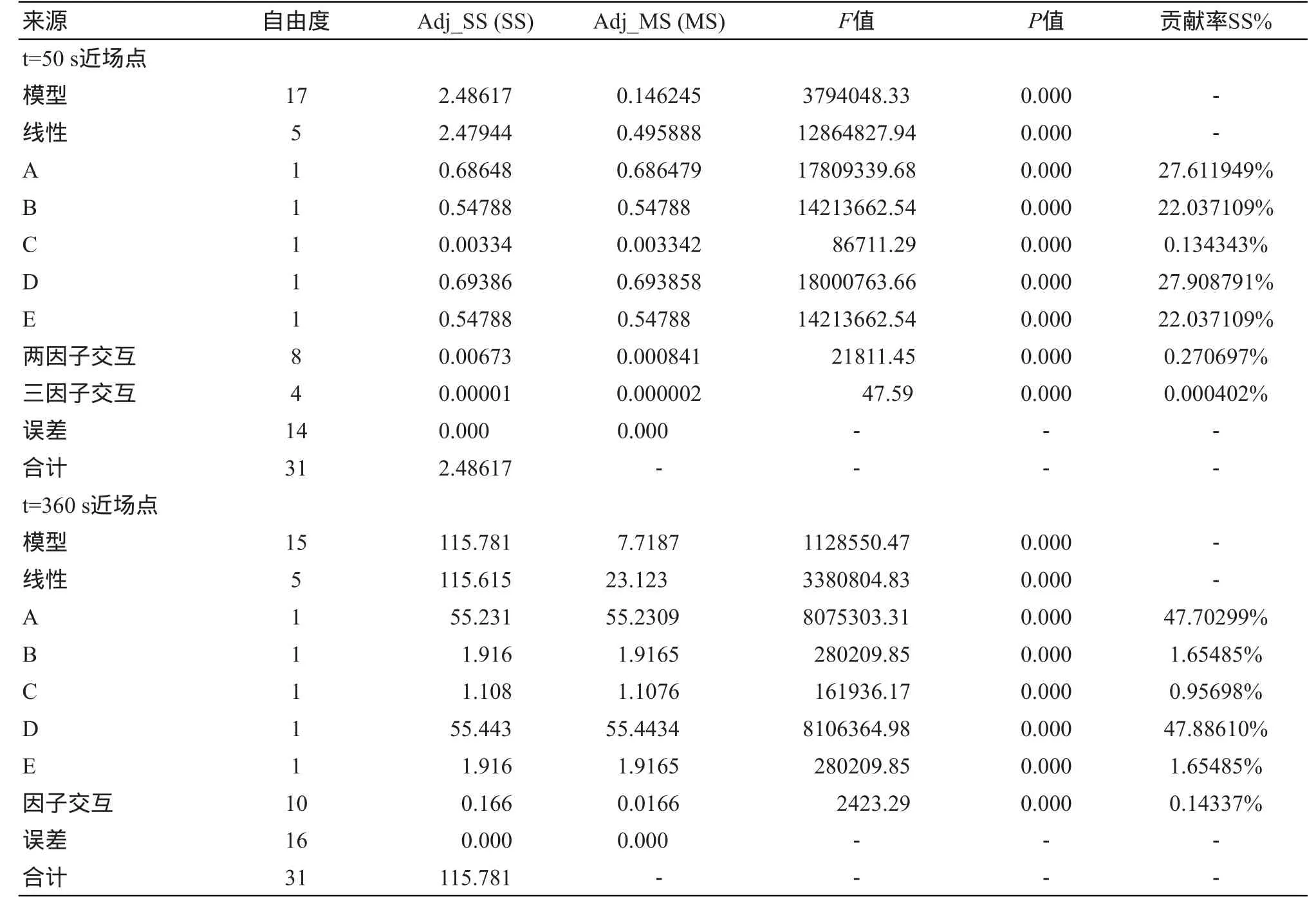
表4 t=50 s以及t=360 s时的近场点方差分析

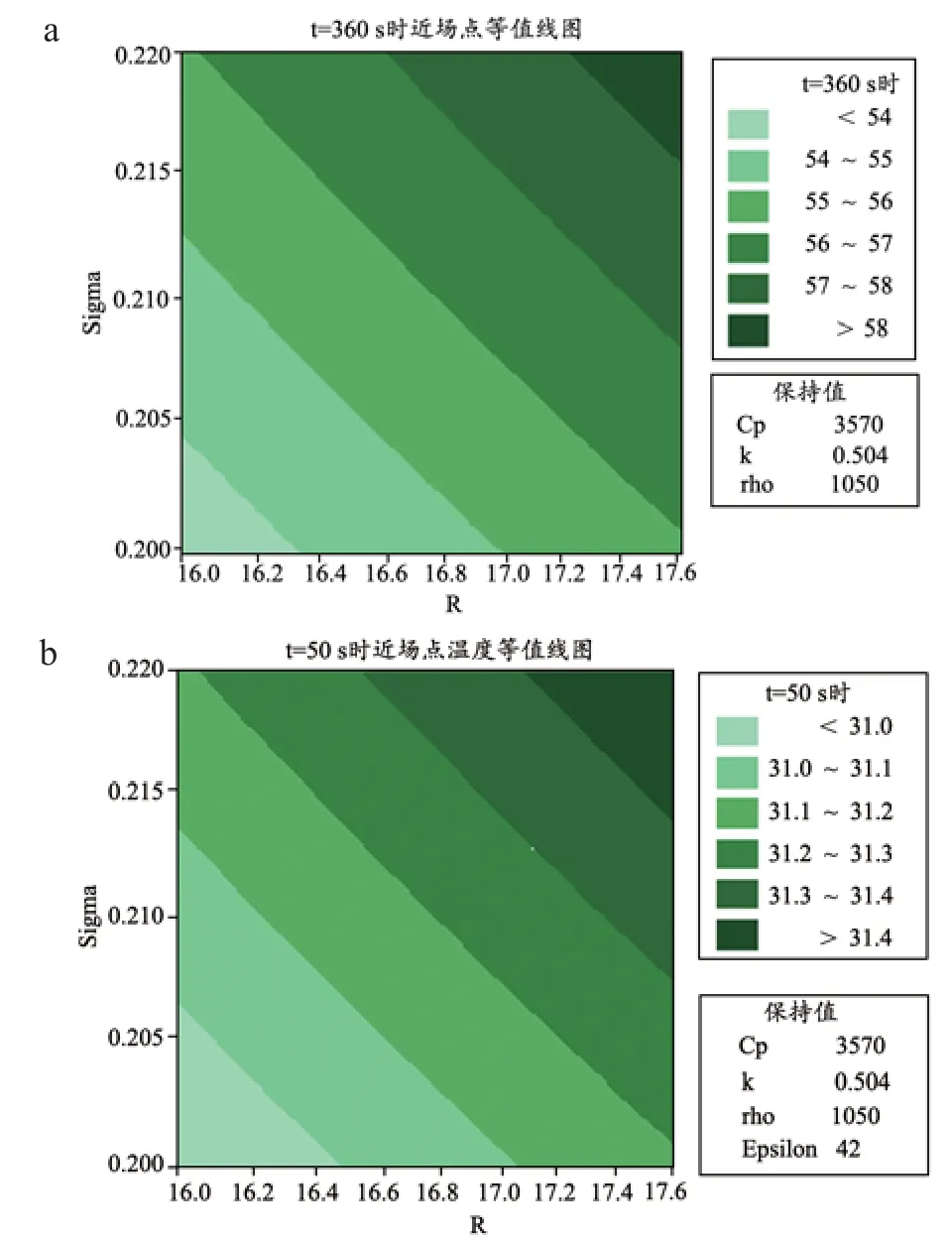
图8 Sigma和R在t=50 s（a）和t=360 s（b）的近场等温线

2.3 各参数对40℃和80℃等温面包容体积的敏感性分析

选取不同位置的点研究特性参数的敏感性，具有特例性，因此本研究进一步讨论了各参数对不同等温面包容体积的敏感性。在热消融手术中，通常选用50℃等温面[14-15]和60℃等温面[16-17]作为消融区边界，即可认为50℃等温面包容体积或60℃等温面包容体积为热损伤组织体积。因此本研究中分别选取40℃等温面和80℃等温面作为近场点和远场点的综合影响效果。各参数在不同时刻对40℃和80℃等温面包容体积的方差贡献率趋势图，见图9～10。如图所示，其中Cp和rho变化趋势相同，在图中重合；R和Sigma的变化趋势十分相近；消融期间参数R和Sigma对等温面包容体积影响一直很显著；Epsilon对等温面包容体积无影响；参数Cp和rho对等温面包容体积影响敏感性随着仿真时间的增加先略有所增加然后变小，整体影响趋势是减小的；这些结果与单点敏感性分析结果具有较好的一致性。

3 结论

本研究基于温控射频热消融仿真模型，分析了包括热参数和电参数在内的特性参数对近场点、远场点和不同等温面包容体积的影响。结果表明，参数Sigma和R在消融期内对各点消融温度的敏感性始终很显著，且成正相关；参数Cp和rho对各点消融温度的敏感性随着仿真时间的增加而减小，且成负相关；参数Epsilon在消融期间内对各点消融温度没有影响。k的变化没有较好的一致性：对于近场点而言，开始阶段通过热传导吸收热量，所以k增加时该点消融温度会升高，成正相关；消融后期通过传热传导释放热量，因此与k成负相关。对于远场点而言，主要通过热传导吸收热量，因此与k成正相关。k对不同等温面包容体积的敏感性在消融前期略有不同，在消融中后期变化趋势基本一致。k的SS%始终很小，可忽略不计，在今后的研究中可将k取为最优固定值。由于Sigma和R在消融期内对消融温度的敏感性很显著，因此在反馈调节中可重点考虑反馈参数Sigma和R。对敏感性不显著的参数如Cp、rho、k和Epsilon可取为最优固定值。

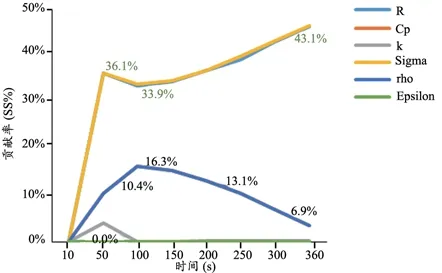
图9 仿真过程中各参数对40℃等温面包容体积方差贡献率趋势图

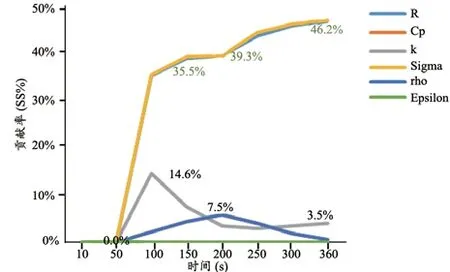
图10 仿真过程中各参数对80℃等温面包容体积方差贡献率趋势图

综上所述，本研究通过敏感性分析获得了温控射频热消融仿真模型中的显著性影响因素Sigma和R，为敏感性参数的反馈调节中提供了科学依据。

[1] 周茂胜,常欣.射频消融原理及应用[J].当代医学,2009,15(21): 18-19.

[2] Clasen S,Rempp H,Schmidt D,et al.Multipolar radiofrequency ablation using internally cooled electrodes in ex vivo bovine liver: correlation between volume of coagulation and amount ofapplied energy[J].Eur J Radiol,2012,81(1):111-113.

[3] Berjano EJ,Hornero F.Thermal-electrical modeling for epicardial atrial radiofrequency ablation[J].IEEE Trans Biomed Eng,2004,51(8):1348-1357.

[4] Matschek J,Bullinger E,Haeseler FV,et al.Mathematical 3D modelling and sensitivity analysis of multipolar radiofrequency ablation in the spine[J].Math Biosci,2017,284:51-60.

[5] 张曼.肿瘤热消融治疗手术规划系统及关键技术研究[D].北京:北京工业大学,2016.

[6] 聂晓慧.脊柱肿瘤射频消融适形治疗的温度场研究[D].北京:北京工业大学,2016.

[7] Jin C,He Z,Liu J.MRI-based finite element simulationon radiofrequency ablation of thyroid cancer[J].Comput Methods Programs Biomed,2014,113(2):529-538.

[8] 黄维,罗洪艳,潘进洪,等.构建基于肝脏CT图像的温控射频消融仿真模型[J].中国介入影像与治疗学,2014,11(8):532-536.

[9] Bueno C,Hauschild MZ,Rossignolo JA,et al.Sensitivity analysis of the use of life cycle impact assessment methods:a case study on building materials[J].J Clean Prod,2016,112(1):2208-2220.

[10] 蔡毅,邢岩,胡丹.敏感性分析综述[J].北京师范大学学报(自然科学版),2008,44(1):1.

[11] 李进霞,张伟杰,张素香.有限元法及应用状况[J].科技创新导报,2012,(31):120-121.

[12] Rossmanna C,Haemmerich D.Review of temperature dependence of thermal properties, dielectric properties,and perfusion of biological tissues at hyperthermic and ablation temperatures[J].Crit Rev Biomed Eng,2014,42(6):467-492.

[13] Cavagnaro M,Pinto R,Lopresto V.Numerical models of microwave thermal ablation procedures[A].Microwave Conference (EuMC),2014 44thEuropean[C].New York:IEEE,2014:480-483.

[14] 包家立.电磁医疗设备的生物物理基础与应用[J].中国医疗设备,2016,31(4):6-13.

[15] Peng T,O’Neill D,Payne S.Mathematical study of the effects of different intrahepatic cooling on thermal ablation zones[A]. International Conference of the IEEE Engineering in Medicine and Biology Society[C].New York:IEEE,2011:6866-6869.

[16] 孙登华,钱锋,孙光,等.射频消融技术的临床应用进展[J].吉林医学,2012,33(13):2823-2825.

[17] Haase S,Süss P,Schwientek J,et al.Radiofrequency ablation planning: An application of semi-infinite modelling techniques[J].Eur J Oper Res,2012,218(3):856-864.

本文编辑 袁隽玲

Parametric Sensitivity Analysis of Simulation Model for Temperature-Controlled Radiofrequency Ablation Temperature Field

WANG Xiaoru, GAO Hongjian, WU Shuicai, BAI Yanping
College of Life Science & Bio-Engineering, Beijing University of Technology, Beijing 100124, China

ObjectiveTo study the sensitivity of the characteristic parameters in the temperature-controlled radiofrequency ablation (RFA) temperature field model and to analyze the signi ficance of these parameters for the temperature distribution.MethodsThe finite element method was used to establish the temperature field simulation model. The variance contribution rate (SS%) and the main effect of the characteristic parameters on the size and the temperature of the ablation area were then discussed based on the variance analysis theory.ResultsThe study showed that in the near field region, the SS% of the electrical conductivity (Sigma) and the tissue equivalent resistance (R) were about 22% in the early ablation session and about 47.5% in the posterior ablation session. In the far field region, the SS% of Sigma and R were about 26.9% and 43% respectively in the early and posterior ablation stage; with regard to ablation area size, the SS% of Sigma and R were about 36% and 46.5% in the early and posterior ablation stage, respectively. According to the main effect analysis, Sigma and R were directly correlated with temperature, speci fic heat capacity and density were inversely-related to temperature, and the correlation between thermal conductivity and temperature varied with time and position.ConclusionDuring in the RFA thermal ablation, compared with the thermal conductivity, density, speci fic heat capacity and dielectric constant, electrical conductivity and tissue equivalent resistance have signi ficant sensitivity.

radiofrequency ablation; temperature field simulation; model parameters; sensitivity analysis

R318

A

10.3969/j.issn.1674-1633.2017.09.006

1674-1633(2017)09-0023-06

2017-05-16

2017-05-23

国家自然科学基金资助项目（71661167001）；北京市自然科学基金资助项目（7174279）。

吴水才，教授，主要研究方向为生物医学信息检测与处理、生物医学电子与医疗仪器，生物医学图像处理。

通讯作者邮箱：wushuicai@bjut.edu.cn