基于NCV门库的可逆逻辑门进化设计与优化

赵曙光，崔 平，罗 霄，李智伟

(东华大学 信息科学与技术学院，上海 201620)

基于NCV门库的可逆逻辑门进化设计与优化

赵曙光，崔 平，罗 霄，李智伟

(东华大学 信息科学与技术学院，上海 201620)

提出和实现了一种基于遗传算法的可逆逻辑门的设计方法。其特点是预先求出并存储所需功能的可逆逻辑门的真值表，并对NCV基本门库中的控制V门，控制V+门，控制非门，非门进行编码，通过这些基本门的级联，构成染色体暨可逆逻辑门，在逐代进化中按照既定逻辑功能和优化目标进行适应度评估，再利用遗传换代中的选择，交叉，变异等功能进行遗传操作，进而找到功能和性能均符合预定目标的可逆逻辑门。实验结果证明，此方法的可行性、有效性，与传统手工设计可逆逻辑门相比，其在求解速度和能力方面有显著提高。

可逆逻辑门；可逆逻辑；NCV门库；遗传算法

量子计算机具有众多优点，其理论基础和技术关键是可逆逻辑门以及可逆逻辑电路。可逆逻辑电路由可逆逻辑门组合与级联构成，因此可以说可逆逻辑门的种类丰富程度直接关系到量子计算机的进步与发展。多年来，众多种可逆逻辑门已被提出，常用的有控制非门[1]、Toffoli[2]门、Fredkin门[3]、Peres门等。随着可逆逻辑技术的不断发展，现有的可逆逻辑门的种类与功能已经难以满足科研与生产的需求。

NCV门库中包含有控制V门，控制V+门，控制非门以及非门这4种量子基本门，当每条量子线输入均为二元基态时，输出却有可能是叠加态[4-5]。量子逻辑基本门的这一特点，使得利用该门库构建可逆逻辑门困难重重。基于量子逻辑门的3量子综合算法相对较多[6-8]，但是基于量子非逻辑门的可逆逻辑门设计算法并不多见。尽管一些专家已经提出了几种基于NCV门库的多量子综合算法[9-12]，但是都存在一定的局限性。

基于上述问题并结合遗传算法，本文提出了基于NCV门库的可逆逻辑门优化设计算法。该算法给出了新的编码方案，简化了算法适应度计算的复杂度，一定程度上提高了算法效率，这对新门的发现以及现有可逆逻辑门库的扩充均有一定意义。

1 可逆逻辑门遗传算法模型的建立

1.1 门库器件以及其选择

Deutsch等人已经证明了低位量子门通过串、并联等方式可实现所有量子门[13]。从理论上来说NCV门库中的量子门完全可以实现所有可逆逻辑门。参照Benchmark[14]标准库里现有可逆逻辑门NCV实现中所用到的基本门种类并以减少收索规模、提高搜索效率为目标，本文选择非门，控制非门，控制V+门，控制V门作为设计与优化可逆逻辑门的基石。

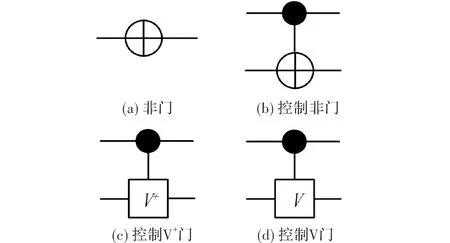
图1 量子门

图1给出了NCV门库中量子门的图形符号其功能概述如下：

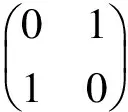
CNOT(CN)门的函数T({c};t)：目标位t翻转的条件是控制位c输入为1。

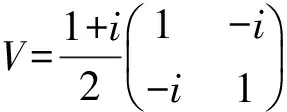
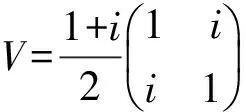
除NOT门外，以上各个量子门在不满足控制位为1的条件时，输出值与输入值相同。

表1 控制量子门的真值表

CV、CV+以及CN的真真值表如表1所示。其中,x1是控制端输入;x2是受控端输入;y1是控制端输出;y2是受控端输出。该表证明CV门和CV+互为共轭转置矩阵，即这两个量子非逻辑门自身或者彼此相连，那么该结构就可以优化。它们的具体基本运算关系如下

V×V=V+×V+=NOT

(1)

V×V+=V+×V=I

(2)

1.2 NCV门的编码

利用进化算法设计可逆逻辑门，需要对所选器件进行编码。结合文献[11]中编码方式，本文提出了另一种编码方式。

除非门外，NCV门库中其余量子门均由两部分组成，分别是控制端和受控端。根据的量子门的这一结构特点以及量子比特在通过量子门时运算的特性，本文提出的编码方案中，也将一个量子门分成控制端和受控端两个部分。为表述方便，本文用字符C表示量子门的控制端，编码方案中用1表示；用字符V+、V、N分别表示量子门CV+、CV、CN的受控端，编码方案中分别用2，3，4表示；NOT门用5表示，直通则用0表示。

对于n输入可逆逻辑门，其每位量子门均可用一个n位列数组{…,x,…,y,… }T表示。该数组中“…”表示n-2个0；如果该量子门为NOT门，则x取0、y取5，其余情况下x、y中一个取1，另一个取2～4中的一个整数值。m组此类数组级联，就可以表示一个 的逻辑门。这种编码方式可使得一个复杂的可逆逻辑门完全可以用一个二维数组存储起来。以图2所示的Toffoli门为例，按照本文提出的编码方案编码，其NCV实现方式的染色体编码是：chr={{1,4,0,1,4},{0,1,1,0,1},{3,0,3,2,0}}。

图2 Toffoli门的编码示意图

1.3 建立遗传算法模型

1.3.1 模型的基本元素

基因：一个基因代表一个量子门。

染色体：一个染色体由多个基因级联组成，表示一个量子门级联结构。

种群：种群由若干染色体组成，其实质是一个量子门级联结构的集合，种群大小由初始生成的种群大小决定。

适应度：适应度是染色体与预期目标的符合程度，本文中表示逻辑门的功能与其预期功能符合程度。

1.3.2 适应度评估准则

对于n输入的染色体，其适应度评估准则如下：

准则1 将初始输入值迭代加载到染色体的各个基因计算输出结果。既染色体头部的第一个基因以初始输入作为输入，之后的基因都以其左相邻基因的输出作为输入根据量子门的真值表计算输出。最后一个基因的输出就是染色体最终的输出，若其等于预期输出，则适应度增加n，记为fit1。

准则2 逻辑门的可逆性。NCV门库中的量子门随机生成的染色体不一定具有可逆的性质，大部分初始染色体内部还会出现量子纠缠现象即该染色体没有完整并确定的输出[9]。因此，把初始输入从染色体的头端(以图2为例，其头端是CV门)开始迭代得到输出结果，然后将输出的结果从染色体的尾端(以图2为例，其头端是CNOT门)开始反向迭代得到输出结果。对比初始输入与第二次输出结果，如果二者相同，则适应度增加n,记为fit2。

准则3 由上述讨论可知，如果染色体相邻两个基因相同，或者CV+、CV相连并且它们级联方式也相同，则此染色体还可以进一步优化。同一条染色体中这种结构每出现一次适应度减少1，记为fit。

按照此3条评价准则以n输入输出的染色体来计算，其适应度计算公式为

(3)

1.3.3 染色体内部量子纠缠的处理

NCV门库中量子门的控制端输入为逻辑值，即控制端的输入均为 或者 时，通过该量子门的量子之间才不会发生量子纠缠[15]。但是随机生成的染色体中各个量子门的级联方式千变万化，量子门之间运算时难免会发生纠缠。这种情况下，量子门输出结果是随机的，表1中通用的真值表不再生效，这将导致可逆逻辑门的设计与优化无法继续。

将初始输入值迭代加载到染色体的各个基因，计算量子门个体适应度这一过程中，需要动态的处理染色体中量子纠缠现象，以便得到内部不发生量子纠缠的染色体。用一个全新的染色体替换当前发生量子纠缠的染色体显然是不现实的，这种替换不能确保新的染色体内部不发生量子纠缠。

为解决这一难题，本文设计了一种强制变异方法：当发生量子纠缠时，在不改变基因种类的情况下随机改该变基因的级联方式，并重新计算该量子门的适应度，直到变异后的染色体内部不再发生量子纠缠。量子纠缠处理流程图如图3所示。

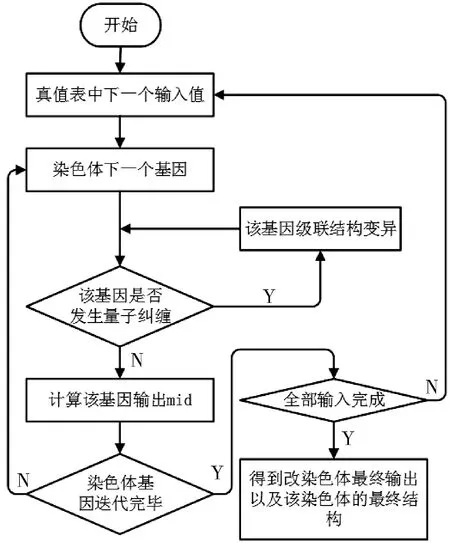
图3 量子纠缠处理流程图

1.4 遗传算法的实现

本文选用轮盘赌法来实现对交叉变异个体的选择。在种群适应度计算完成后程序进入交叉变异阶段。

为保证变异结果能顺利保留到下一代，变异与否直接发生在所选择的两个染色体上。如果满足变异条件，则对该染色体进行变异处理。本设计中实现了两种或不同的变异方式，一种是对单个染色体中的某个基因进行变异操作，即变异过程直接替换该基因；另一种方式是对对种群中的某个染色体进行变异操作，即直接替换掉整个染色体。两种不同的变异方式充分保证了种群的多样性，避免了种群早熟的不良结果。

同理，如果不满足变异条件，则直接进入交叉阶段。交叉发生在经过变异之后的染色体对上。根据染色体的长度，在染色体上随机选取一个交叉位置，两个染色体在该位置互换部分基因完成交叉操作。本代交叉变异之后整个种群进入到下一代遴选，直至得到预期的结果或者程序运行到最大迭代次数这一结束条件，程序退出循环。

2 实验结果分析

实验在VS2012平台上用C语言编程实现。

Benchmark标准库中给出了常见可逆逻辑门的一种NCV实现，利用本算法可以得到该标准库中各个逻辑门的不同的NCV实现形式。

2.1 Toffoli门的通用NCV构成

经过多次实验，本文得出如图4所示的Toffoli门的通用NCV实现方式。

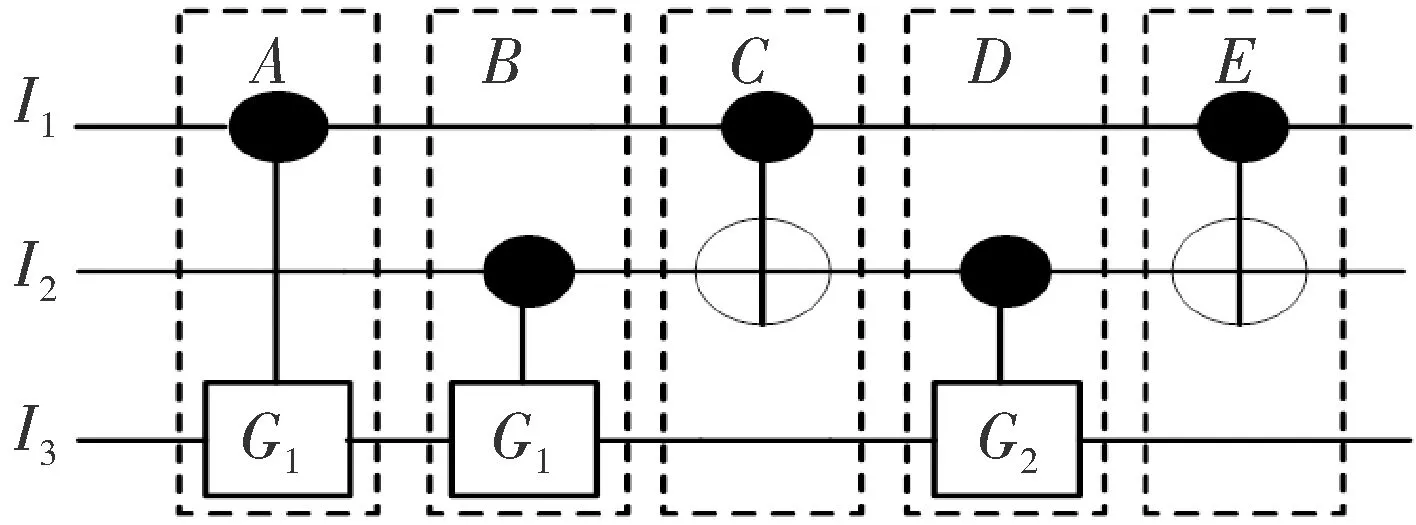
图4 Toffoli门的通用NCV构成形式

该图中G1、G2须分别选择CV或者CV+中的一种。量子门B与C，C与D可互换位置，但不能同时互换；输入端I3可与I1、I2互换位置，以改变受控位位置。

2.2 Fredkin门的通用NCV构成

与Toffoli门类似，实验中也得到了多种Fredkin门的实现形式。图5展示了Fredkin门的两种通用实现方式。这两种实现方式中G1、G2也是分别选择CV或者CV+中的一种。方式1中量子门B与C，C与D，F与G可互换位置，但是B与C，C与D可不可同时互换位置；方式2中量子门B与C可互换位置其余量子门位置相对固定，不能互换。同理，两种方式中输入端位置可以互换，以改变控制位的相对位置。

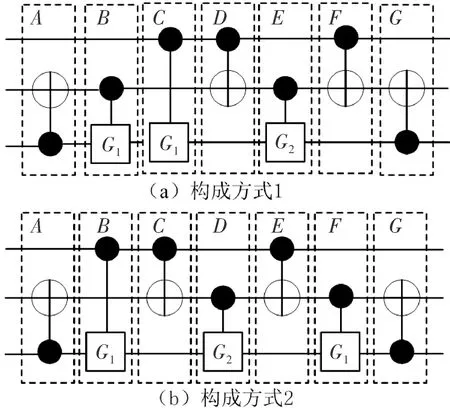
图5 Fredkin门的通用NCV构成形式

2.3 或异或门

该算法不仅是在已有逻辑门的异构形式设计中有较好的表现，在具有新功能的可逆逻辑门设计方面也有较理想的作用

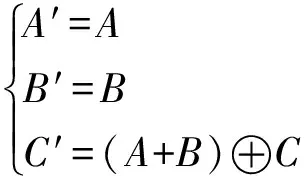
(4)

式(4)定义了一种新的逻辑功能，控制位为A、B，目标位为C。该结构在功能方面实现了C′= (A+B)⊕C，但其具体构成方式未知。经过计算可得该逻辑功能的真值表，如表2所示。

表2 量子逻辑门的真值表

将该真值表输入到本文提出的算法程序中，经过程序的运行可得到该逻辑功能的具体NCV实现，如图6所示。

图6 量子逻辑门的NCV实现

该实现中G1可选择CV或者CV+中的任意一种。该实现中量子门B与C，C与D可互换位置，其余量子门位置相对固定。

事实上，经过对实验结果进行分析，得出结论：可逆逻辑门中相邻的两个量子门，如果它们的控制端在同一条线上，或者受控端在同一条线上，或者控制端与受控端都不在同一条线上，互换这两个量子门的位置可逆逻辑门的功能不变。

3 结束语

针对NCV门库中的量子门的特点，设计了较好的编码方式；经过对遗传算法的改进，适应度评估方法的优化，以及量子纠缠的处理，得到了得到了较为优化的量子可逆逻辑门的自动化设计与优化的方法。该算法不依赖先验知识、不需要人工干预，只要给出所需要的逻辑功能真值表，程序即可生成满足该功能的量子门级联结构，因此其具有较高的搜索、全局优化能力。这为可逆逻辑门库的扩充以、现有可逆逻辑门的优化及新门的设计提供了参考。

[1] Feynman R.Quantum mechanical computer[J].Optic News,1986,16(6): 11-20.

[2] Toffoli T.Reversible computing[D].MA,USA:MIT Lab for Computer Science,1980.

[3] Ekert A K.Quantum cryptography based on Bell’s theorem[J].Physics Review Letter,1991,67(6):661-663.

[4] Zheng Y Z,Ye P,Guo G C.Probabilistic implementation of non-local CNOT operation and entanglement purification [J].Chin Physics Letter,2004,21(4):9-11.

[5] Gao G L, Cai G C, Huang S S, et al. 1→N quantum controlled phase gate realized in a circuit QED system[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(8):1422-1426.

[6] Fredkin E,Toffoli T.Conservative logic[J]. International Journal of Theoretical Physics,1982,21(3):219-253.

[7] 李志强,陈汉武.量子可逆逻辑电路最小代价综合算法[J].东南大学学报,2008,38(2):249-254.

[8] Maslov D,Miler D M.Comparison of the cost metrics through investigation of the relation between optimal NCV and optimal NCT three-qubit reversible circuits[J].IET Computer & digital Techniques,2007,1(2):98-104.

[9] 陈汉武,李文骞,阮越.基于汉明距离递减变换的可逆逻辑综合算法[J].计算机学报,2014,8(37):1839-1845.

[10] 李志强,陈汉武,刘文杰.基于新型量子逻辑门库的最优NCV三量子电路快速综合算法[J].电子学报,2013,4(4):690-697.

[11] 俞经龙,赵曙光,王祥.可逆逻辑门进化设计方法及其CUDA实现[J].电子科技,2015,1(4):12-15.

[12] Wille R.Fast exact Toffoli network synthesis of reversible logic[C]. Grace:International Conference on CAD, 2007.

[13] Miller D M.Lower cost quantum gate realization of multiple-control Toffoli gate[C].PacRim:IEEE Pacific Rim Conference on Communications and Signal Processing,2009.

[14] Wille R, Groβe D, Teuber L, et al. RevLib: An online resource for reversible functions and reversible circuits[C]. Germany:International Conference on CAD, 2008.

[15] 张国锋.量子纠缠的若干问题研究[D].太原:山西大学,2004.

Research on the Evolutionary Design and Optimization Method of Reversible Logic Gates Based on NCV Gate Library

ZHAO Shuguang，CUI Ping，LUO Xiao，LI Zhiwei

(School of Information Science and Technology,Donghua University,Shanghai 201620,China)

A design method of reversible logic gates based on genetic algorithm is proposed and implemented in this paper. Its feature is that given and stored the truth tables in advance of the needed reversible logic gate. Encoding quantum NOT, CNOT, Controlled-V and Controlled-V+ (NCV). Using the base logic gates to construct chromosomes (reversible logic gates). Evaluation fitness according to expect logic function and optimization objectives, and running genetic operations such as selection, crossover and mutation. Thus we can find the reversible logic gate which has corrected function and optimal form. The experimental results give some prove of feasibility and effectiveness of this method. This method is more advantage than traditional manual design in capability and speed.

reversible logic;reversible logic gates;NCV gate library;genetic algorithm

2016- 11- 16

国家自然科学基金(61272224)

赵曙光(1965-)，男，博士，教授。研究方向: 电子设计自动化等。崔平(1990-)，男，硕士研究生。研究方向：可逆逻辑门的自动化设计等。

10.16180/j.cnki.issn1007-7820.2017.09.001

TN79;TP302.2

A

1007-7820(2017)09-001-05