基于PKI的RSA加密算法研究

◆周 亮

(六九零二科技有限公司 江苏 210000)

基于PKI的RSA加密算法研究

◆周 亮

(六九零二科技有限公司 江苏 210000)

因Internet技术及移动设备的爆发式发展，信息安全面临的威胁日益严重。PKI（公钥基础设施）自成体系，具有统一的规范和安全认证标准，从技术上解决实时在线身份鉴证、信息完整性检查和抗抵赖等安全问题。成熟有效的加解密算法是核心，为基于网络的活动提供可靠的安全保障。RSA加密算法是目前网络上进行通信保密传输和数字签名的最有效的安全算法之一，具有成熟度高、安全性高、易于理解等特点。

PKI；公钥基础设施；RSA；加密；解密

0 引言

PKI是一种利用公钥理论和技术建立的提供信息安全服务的安全基础设施，能提供身份认证、数据保密、数据完整性及不可否认性等服务。我国电子商务、电子政务、网上银行、网上支付和网上证券等都对信息保密有极高的要求。国家的863计划中就专门为PKI立项来支持PKI研究和发展。加解密算法是构成这一系列关键部件的核心。本文分析了目前网络传输最适用的RSA加密算法。

1 RSA算法概述

RSA的安全性基于数论中大素数分解的困难性，其公开密钥和私人密钥是一对大素数（100到200个十进制数或更大）的函数。从一个公开密钥和密文中恢复出明文的难度等价于分解两个大素数之积。

1.1 RSA算法的描述

RSA算法的明文和密文空间就是0到（n-1）之间的整数值，显然，RSA算法是属于分组密码体制的。我们把明文、密文分组分别用M、C表示，公钥、私钥参数分别用e、d表示，那么RSA算法可以简单的叙述为：

加密

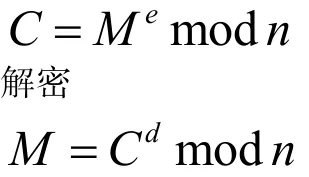
其中n是两个非常大的两素数之积。要计算出大素数的积是十分容易的，但是要分解两大素数之积却是很困难的，所以其安全性是基于整数的因子分解困难性的。

1.2 RSA算法的实现

我们从如下几个方面阐述RSA算法：如何构成算法的参数、如何加密、如何解密。

1.2.1 参数的构成

选取两个大素数P、Q。

计算n: n=p.q。

随即选取e，满足1＜e＜φ(n), gcd(e, φ(n) )=1，那么公钥就是(e,n)。

计算d：满足ed=1 modφ(n)，那么私钥就是(d,n)。

最后销毁P、Q、φ(n)；自己保存好私钥（d，n），公开公钥（e，n）。其中，φ是欧拉函数：φ(n)=（P-1）（Q-1）。RSA算法不论用于加密解密，还是用于数字签名，其明文和密文空间就是0到（n-1）之间的整数值。

1.2.2 加密

现在对消息m加密，按照下列步骤进行：

把消息m分组为i=1,2,…，一般取的比特长度刚好小于n的比特长度。

明文m就是的连接，i=1，2，…。

密文C就是的连接，i=1，2，…。

1.2.3 解密

下面是对密文C的解密步骤：

把C分组为，i=1，2，…，的比特长度刚好小于n的比特长度。

2 RSA算法中的基础算法

RSA中的一些基础算法构成了RSA算法的核心，例如模幂算法、斯泰因算法和米勒-勒宾算法等。

2.1 模幂算法

算法思想如下，求x^r(mod p)：

赋值a=x,b=r,c=1。

判断b=0?

若b=0,则输出c;若b不等于0则做b(mod 2)运算。

判断b(mod 2)的结果是否为0?

若b(mod 2)等于0，则做b=b/2,a=a^2(mod p)；并且将b的新值从4)重新进行b(mod 2)的运算判断。

若不等于0，则做b=b-1,c=ac(mod p)；并且将b的新值从2)重新进行b=0?的判断。

重复以上过程，直到b=0，然后输出得到的c，则c就是所求的x^r(mod p)值。

2.2 斯泰因(Stein)算法

求解gcd{n1,n2}的斯泰因（Stein）算法思想如下：

已知：n1=＞0,n2＞0

c=0

若n1，n2都是偶数，则做n1=n1/2, n2=n2/2, c=c+1; 转2)循环。若条件否转到3)

若n2是偶数，则做t=n1,n1=n2,n2=t。若条件否转4)若n1是偶数，则做n1=n1/2;转4)循环。若条件否转5)若n1-n2＜0，则做t=n1,n1=n2,n2=t。若条件否转6)

n1=(n1-n2)/2

若n1=0，则做g=2^c*n2,输出g，结束。若条件否转4)

2.3 米勒-勒宾(Miller-Rabin)素数测试算法

令n-1=2^s*m,其中s是非负整数，m是正奇数。若b^m=1(mod n)，0＜=b＜=n-1,则n称通过以b为基的米勒-勒宾（Miller-Rabin）测试。

已知：n-1=2^s*m

在{1,2,....,n-1}中随机均匀地产生数b；计算v＜=b^m(mod n)

若v==1，则转到7)

i=1

若v==n-1，则转7)

若i==s,则n非素数，结束

v=v^2(mod n),i=i++,转4)

n通过测试

3 实验分析

本文使用C++语言实现了上述算法，并正确运行，运行过程和结果如图1所示。

4 结论

加密算法是当前蓬勃发展商业、医疗、政企和航空航天等各行各业信息安全的坚实基础，对各种加密算法的研究有助于有效利用和完善我国的安全认证和信息安全保密体系，促进其更快地发展。

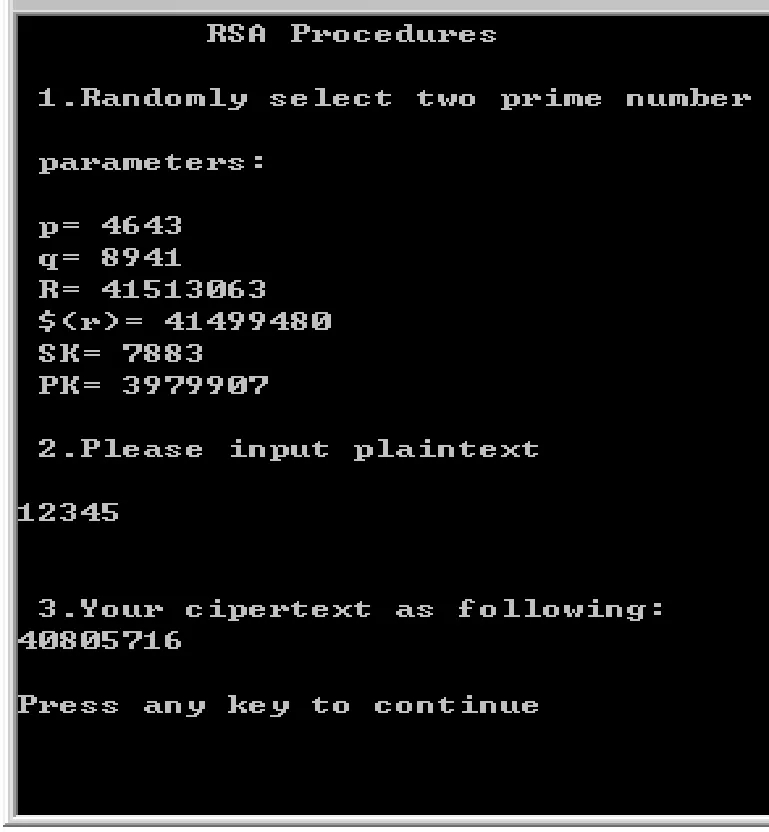
图1 RSA算法实现

[1]张先红.数字签名原理及技术[M].北京：机械工业出版社，2004.

[2]Andrew Nash等，张玉清等译.公钥基础设施（PKI）：实现和管理电子安全[M].北京：清华大学出版社，2002.

[3]冯登国，林东岱，吴文玲.欧洲信息安全算法工程[M].北京：科学出版社，2003.

[4]谢冬青，冷健.PKI原理与技术[M].北京：清华大学出版社，2004.