灰色误差理论在岩矿测试数据处理中的应用

杨正良

(贵州有色地质化验监测中心，贵州 都匀 558004)

在对岩矿测试数据处理过程中，为了确保数据处理的准确性和可靠性，近年来新的数据处理方法不断涌现，其中灰色误差理论在数据处理方面，发挥了重要的功能和作用。文章对灰色误差理论的应用研究，注重把握灰色误差理论的概念和内涵，借助于灰色误差理论的实例分析，对该法的优势进行把握，以提升岩矿测试数据处理的精确度。

1 灰色误差理论基本理论分析

灰色误差理论与传统的统计学理论不同，能够对小样本进行有效地数据分析，是一种非统计理论的处理方法。灰色误差理论介于信息完全明确和信息不完全明确之间，一部分信息已知，另一部分信息未知的情况下，能够对小样本数据进行很好地处理，得到的数据具有一定的精确性。在进行岩矿测试过程中，一些数据获得可能受到仪器、地质情况等因素影响，导致部分信息不明确，借助于灰色误差理论，利用理论值对未知数据进行替代，是岩矿测量分析的关键。同时，灰色误差理论在数据分析过程中，运算过程简单，要比统计学理论方便很多，这为灰色误差理论在岩矿测试数据处理中的应用创造了有利条件[1]。

从灰色误差理论的本质来看，灰色误差理论对不确定信息进行研究，是一门应用数学。灰色误差理论考虑到了岩矿测试数据处理的实际情况，对一些匮乏的数据信息进行把握，通过对一定区域变化的灰色数进行分析，能够使数据的精确度得到提升[2]。灰色误差理论需要对关联性因素进行把握，注重对事物的发展趋势和客观变化进行描述和评价，根据一定的规律，实现对数据的精确预测。灰色误差理论的一般定义如下：

E(误差)=E(测量值)-E(真实值)

(1)

公式中，E为灰色量。在进行岩矿测试过程中，对误差值予以忽略不计，从理想角度出发，对测量序列设为：

Y(0)={d，d，......，d}

(2)

公式中，d表示测量的真实数值。

在进行岩矿测试数据处理过程中，误差的存在，每个测量值接近于真实值，但并不是真实值，其与真实值之间存在着一定的分散关系。针对于这一情况，可对其进行按照升序排列的方式，对其序列进行处理，得到：

X(0)={d+δ1，d+δ2，d+δ3......，d+δn}

(3)

在上述公式中，δ主要表示了测量的随机误差，这一误差值会对实际的测试结果产生影响。在对灰色误差理论应用过程中，对误差值的评定，需要借助对标准测量不确定度进行把握。这一过程中，针对于公式(2)，对其进行一次累加，得到：

Y(1)={1d，2d，3d，4d，5d......，nd}

(4)

累加后的方程为：

Y(1)k=dk

(5)

灰色误差理论在岩矿测试数据处理过程中，要注重对E(灰色量)以及X(0)、Y(0)等序列进行把握，对系统误差进行有效判断，从而使灰色误差理论在分析过程中，使数据的精确度得到较好的提升。

2 系统误差值的判断

岩矿测试数据处理过程中，系统误差值的判断，是灰色误差理论应用必须把握的一个重点内容。系统误差值判断过程中，可从以下内容予以把握。

假设岩矿测试的数据信息有两组，两组数据分别为：

X1={X1(0)，X1(1)，X1(2)，X1(3)，

X1(4)......X1(k)}

X2={X2(0)，X2(1)，X2(2)，X2(3)，

X2(4)......X2(k)}

在对系统误差进行处理过程中，需要对X1和X2两组数据之间的相关程度进行把握，把握相关程度的基础上，对灰色关联度予以把握。在具体操作过程中，将X1的第一个数据X1(0)作为参考数据，则有：

△i(k)=|X1(k)-X1(0)|

(6)

公式(6)中的i表示了测量数列的序列号，而k则表示了测量数据的个数。系统误差值判断过程中，对△i(k)=|X1(k)-X1(0)|数列中的二级最大值和最小值进行选择，即：maximaxk△i(k)、minimink△i(k)取分辨系数，分辨系数为0.5，根据关联系数，得出系统误差值的计算公式：

ΓXi(k)，X1(0)=minimink|X1(k)-X1(0)|+ξmaximaxk|X1(k)-X1(0)|/|X1(k)-X1(0)|+

ξmaximaxk|X1(k)-X1(0)|

(7)

通过利用公式(7)能够得出ΓXi(k)，X1(0)的关联系数，从而对数列的关联系度进行把握，即：

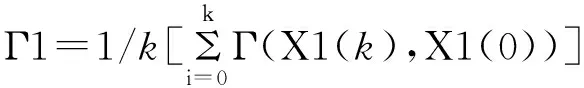
(8)

通过计算，数列的关联度比较接近，则表明测量的序列中不存在显著的误差。通过对系统误差值的把握，能够进一步对小样本岩矿测试数据处理的精准度进行提升，为实际工作提供有效的数据支撑[3]。

3 应用分析

灰色误差理论在岩矿测试数据处理中应用时，注重对随机变量问题予以把握，将这一随机变量看作是一定范围内的灰色数。在借助于灰色误差理论进行数据分析过程中，数据虽然具有一定的复杂性，并且具有离乱特征，但是从整体角度来看，数据之间存在一定的有序性，这种有序性为灰色误差理论分析提供了有效参照。在对岩矿测试数据处理过程中，把握数据之间的有序性，对原始数据处理后，把握数据之间的规律，能够对岩矿变化过程做出相应的描述和评价。灰色误差理论在数据处理过程中，主要采用了累加生成和累减生成的方法，使无规律的原始数据能够有规律可循。

岩矿测试过程中，涉及到了物理和化学的定性，数据测量具有定量关系。对比传统测量方法来看，统计方法在数据处理过程中，会对数据的正态分布情况进行把握，并以此作为统计学理论分析的基础。这种情况下，要求的数据量较大。而在实际分析过程中，小样本数据量的情况较为普遍，在一些特殊地区，获取的测量数据只有3～7个。这样一来，在对数据处理过程中，由于数据的特殊性，加之其与统计学方法要求的正态分布特性有着一定的差异性，导致数据处理可能面临较大的误差，不利于实际操作。

结合灰色误差理论，将其在岩矿测试数据处理过程中应用时，以铜矿石的Co岩矿化学分析数据作为研究对象，根据其标准值情况，对其采用标准测量不确定度评定的方法，对岩矿测试数据进行研究。在测量数据选择方面，以2个数据列作为研究，对Au测试数据进行把握，从而使数据分析的精确度得到更好地提升[4]。在利用灰色误差理论对岩矿测试数据处理过程中，首先需要对数据序列进行生成，结合系统误差值判断方面的研究，选择两个数列，即X1和X2数据选择过程中，每组分别有9个数据，在对其进行灰色分析模型构建过程中，具体的数据序列情况如下所示：

X1=|2.01，2.23，2.35，2.36，2.59，2.61，2.64，2.80，2.89|；

X2=|2.14，2.22，2.43，2.62，2.67，2.70，2.70，2.85，3.09|；

在对数据分析过程中，X1的平均值为2.50；相对标准差为0.27；X2的平均值为2.50；相对标准差为0.28。在对X1和X2的数据进行灰色关联度分析过程中，假设数据在第p个测量点出现转折，针对于这一情况，对p进行取值时，则有：

P=(n+1)/2

(9)

公式(9)中，n表示了测量序列的数据个数，本次试验中，X1和X2每组有9个数据，则n=9，结合P=(n+1)/2=(9+1)/2=5，X1和X2两组数列的转折点为5。在对最大距离求解过程中，根据公式：

△(k)=|X(1)(k)-Y(1)(k)|

(10)

可以得到最大距离△max=1.03。接下来，在对测量数据进行分析过程中，要注重对粗大误差问题予以把握。测得的数据X1(1)=2.01，X1(9)=2.89，借助于公式：

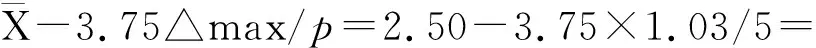
1.727 5；

3.75×1.03/9-5=19.034 375；

X(1)(n-1)=2.01×8=16.08；

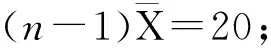
则有1.727 5<2.01<2.50，16.08<19.034 375<20，由此可以看出，测得的数据不含有粗大误差。在对X1的数据处理完成后，接下来对X2的数据进行处理，根据公式(9)，X2的n=9，转折点p=5，△max=1.02，根据数据X2(1)=2.14和X2(9)=3.09，需要对其是否存在粗大误差进行判断。

1.735；

3.75×1.02/9-5=19.043 75；

X(1)(n-1)=2.14×8=17.12；

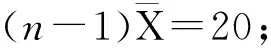
则有1.735<2.14<2.50，17.12<19.043 75<20，表明X2不含有粗大误差。

在对X1和X2是否具有粗大误差问题处理后，接下来需要对误差进行系统性检验。在对误差进行系统性检验过程中，根据公式(7)：

ΓXi(k)，X1(0)=minimink|X1(k)-X1(0)|+ξmaximaxk|X1(k)-X1(0)|/|X1(k)-X1(0)|+ξmaximaxk|X1(k)-X1(0)|，

得到关联系度=|0.570，0.511|，并且0.570-0.511=0.059<0.1，说明X1和X2之间不存在显著误差。

对数据的粗大误差和系统性误差判断之后，需要进行标准量不确定度的评定。在这一过程中，需要对其测量次数进行把握，共计测量7次，之后将获取的数据序列与数据序列X1和X2进行对比，从而对最终的数据进行应用。关于7次的标准测量不确定度情况，如表1所示：

表1 7次标准测量不确定度统计

从表1的统计结果来看，标准测量不确定的数值越大，表明数据的分散程度越大。在对标准测量不确定度应用于岩矿测试数据处理过程中，为了降低误差，可对每组的数列进行单独绘图分析，从而对其精度予以把握，以满足研究的实际需要。

4 结 论

灰色误差理论在岩矿测试数据处理中的应用，要注重对灰色误差理论的基本内涵予以把握，注重对已知信息进行利用，从而对未知信息进行有效地分析，以改变传统统计学理论分析过程中存在的困难性，使岩矿测试数据处理更加方便、快捷。在实际应用过程中，要注重对数列的粗大误差和系统性误差进行把握，在确保数据不存在粗大误差的情况下，对系统性误差进行分析，为标准测量不确定度分析提供支撑，保证岩矿测试数据处理更具针对性。