基于模糊推理过程神经网络的沉积微相判别

刘凌云,许少华,2

(1.东北石油大学 计算机与信息技术学院，黑龙江 大庆 163000；2.山东科技大学 信息科学与工程学院，山东 青岛 266000)

基于模糊推理过程神经网络的沉积微相判别

刘凌云1,许少华1,2

(1.东北石油大学 计算机与信息技术学院，黑龙江 大庆 163000；2.山东科技大学 信息科学与工程学院，山东 青岛 266000)

迄今，现有的油田进行沉积微相模式识别时大多选取测井曲线的静态定量数据，其难以反映测井相的深度累积效应对沉积微相模式识别的影响。针对上述不足，选取测井曲线中可处理的定量与定性混合过程信息，构建并提出了模糊推理和过程神经网络相结合的判别模型，以实现沉积微相的判别。该模型基于模糊集理论对测井相的定性信息进行定量处理，以简化判别规则，并提取有效的判别数据，从而提高沉积微相判别的精度；根据测井相数据随深度变化的特征曲线，采用过程神经网络的过程式输入优势，通过不断优化过程神经网络的学习机制来提高沉积微相判别的准确度。实验结果表明，基于模糊推理过程神经网络模型的沉积微相模式识别方法精度高、速度快，是一种比较实用的沉积微相识别方法。

模糊推理；过程神经网络；学习算法；沉积微相判别

0 引 言

对于正在进行勘探开发的油田，沉积微相判别有助于工作人员了解油井的地下油层结构并分析储层特性[1]；随着油气田勘探开发程度的逐年提高，越发增加了寻找储集相带的难度，为解决这一难题，就必须对储层进行沉积微相分析[2]。通过分析沉积微相的特性，不仅有利于从形成原因对砂体的展布、几何形态、大小、纵横向连通性等特征进行分析[3]，而且，通过对储层内部的非均质性及其变化进行预测，提高了油气采收率[4]。

近年来，伴随着计算机及人工智能技术的飞速发展,沉积相解释中也采用基于神经网络的模式识别方法。但对于复杂多变的地层环境来说，测井相的定量数据转化为地质相数据往往存在误差[5]。现有的微相识别模型大都只依赖于小层定量测井曲线数据，难以融合专家认知和区域地质特征，鲁棒性和容错能力也较差[6]。并且，测井相随深度不断变化的过程实际上是一个不断随深度进行累积的过程。但是现有的沉积微相判别方难以反映深度指标实际存在的累积效应对其产生的影响[7]。

针对上述方法的局限性，提出了新的判别模型—基于模糊推理的过程神经网络模型。该模型不仅考虑到测井相到地质相转换的模糊性，还能与专家知识相融合，并且可以利用过程神经元的学习机制来实现对模糊信息或领域规则的动态信息进行模糊推理，从而提高预测精度。以自动判别地质研究中的测井沉积微相为例，结合实际资料，模糊推理过程神经网络模型处理结果验证了算法的可行性和有效性[8]。

1 模糊推理过程神经网络基本原理

神经生物学的相关研究显示[9]，生物的神经系统所处理的混合模拟信号是由定量和定性信息组成的，仅用单一的数值运算对其处理过程进行解释是片面的，比较全面的说法是在生物神经系统接收到外部环境的激励信号后，结合神经系统内已有的知识，采用自身的信号处理识别模式来实现对输入信息的逻辑运算和推理；并且，生物神经元作为生物神经体系的组成部分，突触收到外界刺激后作出的反应与输入脉冲的相对定时有关，即输出动作变化依赖于持续一段时间内的输入过程[10]。

结合实际问题进行分析，为使判别模型能够像生物神经那样处理含有过程性领域规则或模糊信息的动态信息，提出了模糊推理的过程推理神经元模型。模糊推理过程神经元与过程神经元相比，其优势在于处理的信息不在是单一信息，而是将数值型过程信息与模糊过程推理的相关规则进行融合，反复对过程神经元进行训练，进而实现对过程性数值与模糊混合信号的自适应模糊推理[11-12]。

1.1模糊推理过程神经元模型

以模糊加权过程推理的规则为核心处理机制的模糊推理过程神经元(FRPN),其输出结果和输入条件的定性谓词中包含过程信号的模糊集[13]。在此类能够进行模糊推理的过程神经元中,用模糊逻辑规则来表示论域的“过程知识”,带有模糊性和过程性的输入信号经加权聚合处理后得到一个模糊谓词,当规则真度满足应用阈限时,依据推理规则产生相应的“过程动作”[14]。FRPN的结构如图1所示。

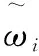
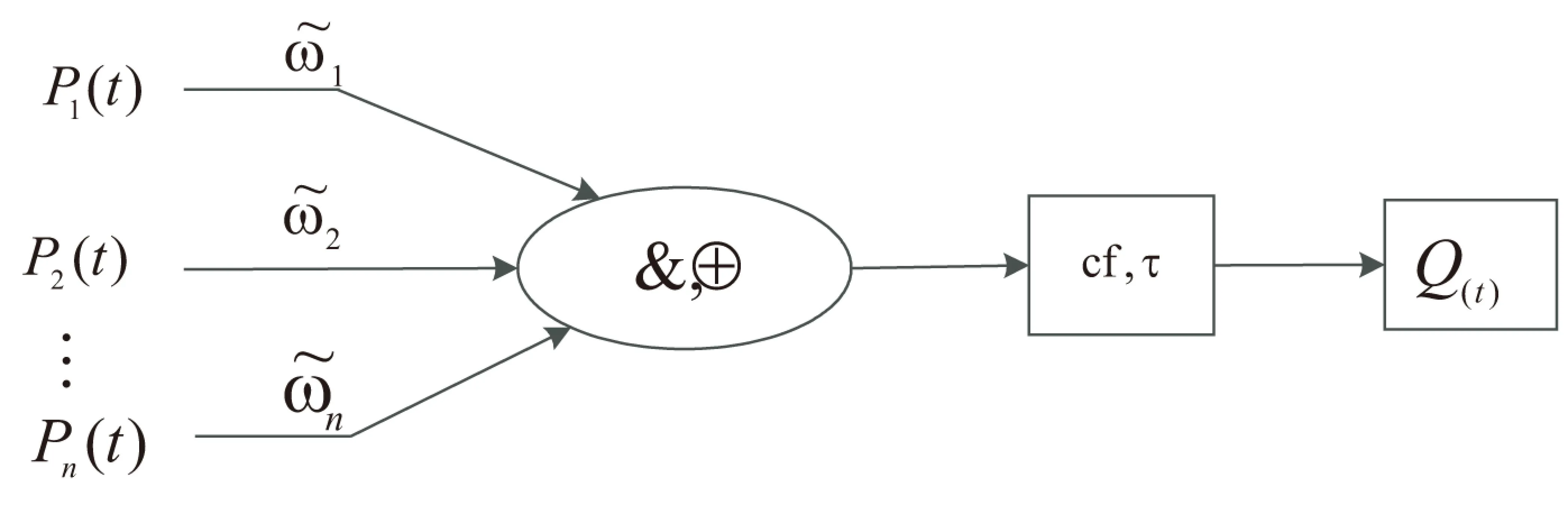
图1 过程神经元

依据图1可得,在FRPN中，模糊过程推理所描述的规则为：

(1)

模糊推理过程神经元由于具备神经元向现实环境不断学习的特性和模糊推理机制等特点，因而选择不同的模糊聚合算子和调整模糊权值来适应实际问题。模糊过程推理规则与加权模糊推理过程神经元一一对应，模糊推理过程神经网络模型由多个模糊过程神经元按照一定的结构关系组成，即构成一个模糊过程推理系统(规则集)[12,16]。

1.2模糊推理过程神经网络模型

模糊推理过程神经网络是指将若干个加权模糊推理过程神经元按照既定的推理规则组织构建的网络模型[17]。如有n个模糊过程推理的前件作为模型输入，m个推理结果作为模型输出，该模型结构如图2所示。

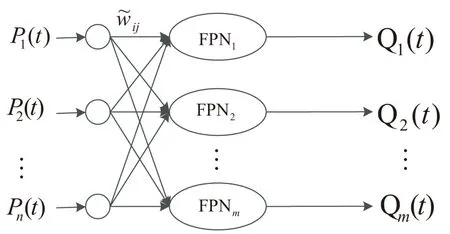
图2 模糊推理过程神经元模型

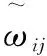
加权模糊推理过程神经网络模型在本质上表达的是一个带有时间信息的加权模糊逻辑规则集，也可以理解为规则知识库[18]。

在现实应用中，对于通过对特定相关数据进行分析，进而获得满足需求的新的模糊推理规则来说，则可以在原来的推理网络的基础上，通过加入新的节点和连接权的形式加入其中。伴随着对研究问题学习的不断深入，越来越多的推理知识将被加入到加权模糊推理过程神经元网络模型中，进而提高该模型解决实际问题的能力。

1.3学习算法

模糊推理过程神经网络模型的推理过程在一定程度上可以与如下方程组的真值计算问题进行相互转化。

(2)

其中，cfj为第j条模糊推理规则的信度因子；T(Pi(t))为前提的真度；T(Qj(t))为结论的真度。

为使判别结果与实际情况最为接近，是以此判别模型达到与之相对应的泛化要求，为此，选取大量的学习样本对模型进行训练，故仅考虑k>n的情况即可。因此，需要解一个超定线性方程组来定网络模型中的参数,利用加权模糊逻辑推理的含义将式(2)转化为如下的超定方程组：

(3)

将解上述方程组转化为解线性规划问题即可，误差方程为:

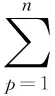
(4)

依据最小二乘原理，使式(4)误差平方和最小,即:

(5)

基于多元函数极值需要满足的充分条件得出:

(6)

将上述方程进行整理，得：

(7)

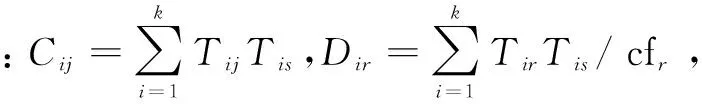
(8)

式(8)将超定方程组转换为含n2个未知数的n2个方程的正规方程组，目前，对于式(8)的求解方法已经相当成熟，高斯-赛德尔迭代法[19]的迭代式如下：

(9)

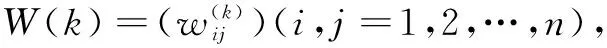
2 模糊推理过程神经网络模型在沉积微相模式识别中的应用

在油田开发研究中，依据测井资料对小层沉积微相进行识别是一项很重要的工作，其方法是基于多个随深度变化、反映油层物理性质的测井变量[20]，根据其连续采样数据的幅值和形态特征及其组合关系来确定小层微相类型。对于层状砂岩油田来说，砂体沉积的主要微相类型分为主体河道砂、小型河道砂、废弃河道砂、河间薄层砂[21]，根据理论分析和现场统计结果,能反映沉积微相的主要变量是随深度不断变化的自然电位(SP)、2.5 m电阻率(R25)、微电极之差(Rmt-Rmd)等测井量化测量数据，以及小层相对厚度h、沉积韵律S等测井曲线定性形态特征。测井曲线如图3所示。

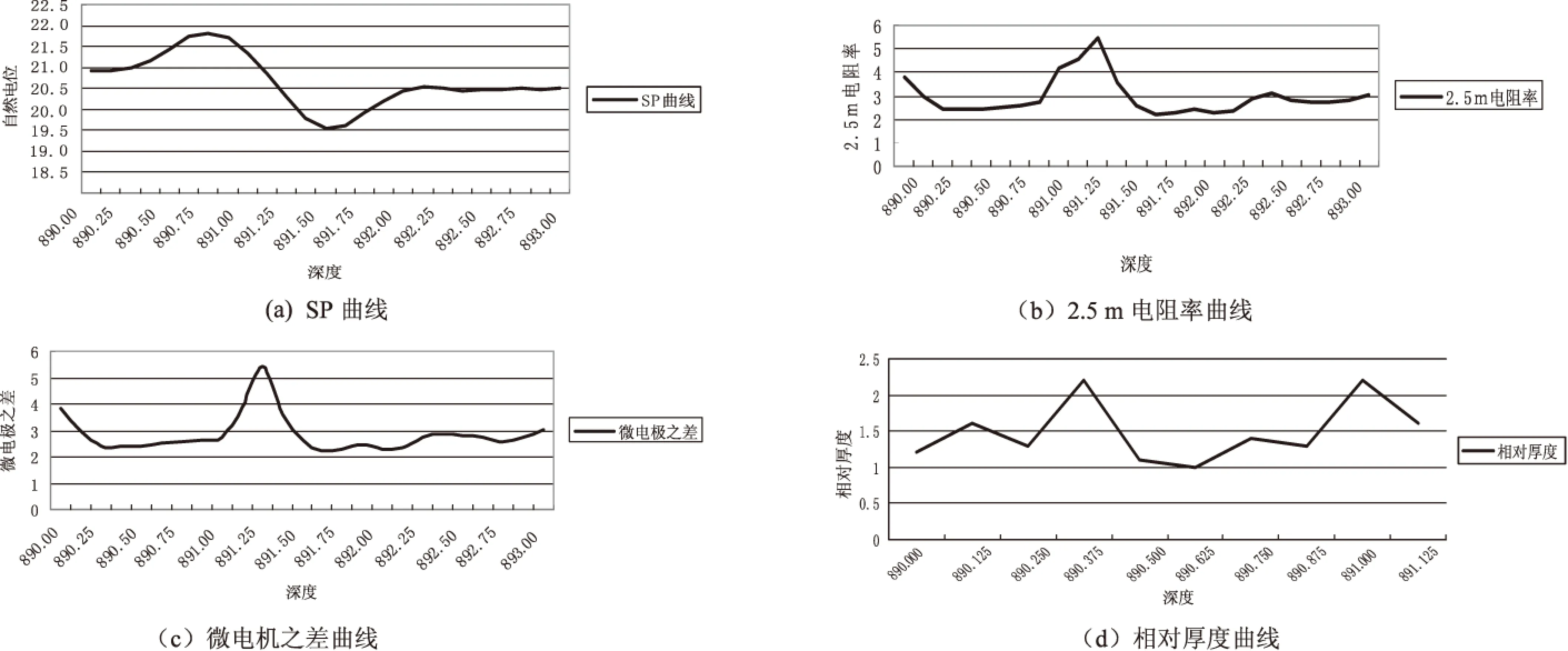
图3 测井曲线

采用FRPN进行沉积微相判别。网络模型输入谓词为随深度变化的测井函数，输出谓词为主体河道砂、小型河道砂、废弃河道砂、河间薄层砂(分别对应j=1,2,3,4),通过高斯隶属度函数对网络输入进行模糊化处理，即:

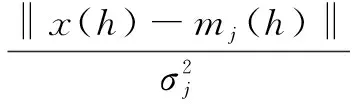
(10)

其中，x(h)为测井曲线函数；由高斯隶属度函数的定义,在对归一化连续输入信号进行模糊化处理时，具有对输入曲线与典型特征曲线进行模态相似性比对的特性。

由此，将训练样本集中的同类函数样本归为一类，取其隶属度的平均值作为规则的真度。

专家认识可归纳如表1所示。

表1 沉积微相特征归纳表

将上述判别模型应用到油田，训练样本集由10口取心井的测井曲线及部分地质报告数据组成。所选样本在一定程度上满足不同厚度、不同沉积韵律的要求，同时按比例较为均匀覆盖了沉积微相的4种类型[22]。抽取样本集中412个样本构成训练集，测试集由剩下的198个样本组成。在资料数据处理时，按照油田规范对小层各测井数据进行取值，小层曲线形态特征根据实验油田已建立的沉积韵律测井曲线模板库实现自动识别。由此，输入函数经模糊处理后得到5个新的输入谓词，还有结论中4个输出谓词,即该模型共涉及9个谓词。所以，超定方程组中的方程个数为81。针对训练集中5类函数样本，分别计算样本隶属度并求其平均值，得到各规则真度为0.75,0.81,0.72，0.70，0.78；规则应用阈限均取0.65。采用高斯-塞德尔迭代算法求解式(8)，最大学习次数设为5 500，迭代精度设为0.009，模型迭代1 543次后收敛。用测试样本集对训练好的网络模型进行测试，输入50个样本，判别正确的样本个数为42，识别正确率为84%。因此，判别结果较好。

3 结束语

对于油田，由于影响沉积微相判别的因素很多，各种因素之间通常是不确定、非线性的复杂关系。除此之外，传统的沉积微相判别预测方法又难以反映测井相指标实际存在的深度累积效应对其产生的影响。针对上述问题，为满足定量与定性混合过程信息的融合信息处理要求，在分析研究基础上，提出了结合过程神经网络的定量信息处理技术与模糊逻辑推理方法的模糊推理过程神经网络模型。实验结果表明，该模型对于处理沉积微相模式识别问题具有很好的识别效果，显著提高了预测精度，是一种比较实用的判别模型。

[1] 宋 翔.基于神经网络与图形处理技术的沉积微相识别系统[D].长春:吉林大学，2004.

[2] 耿 茜.安塞油田桥19井区长3油层组沉积相与油气聚集规律研究[D].西安:西安石油大学，2015.

[3] 程 超,胡望水,秦 刚,等.精细油藏描述中的沉积微相研究—以吉林油田大208区黑帝庙油层为例[J].石油地质与工程,2009,23(2):26-28.

[4] 高宪伟.应用测井资料定量识别碳酸盐岩沉积微相的方法研究[D].成都:成都理工大学，2013．

[5] 孙铁军,冯庆付,刘 浩,等.利用测井资料计算机自动识别沉积微相方法研究[J].西北地质,2010,43(3):132-140.

[6] 许少华,陈 妍,许 辰,等.一种基于正向云变换的混合计算神经网络及其应用[J].计算机与数字工程,2014,42(12):2284-2288.

[7] 许少华,毕聪聪,张 宇,等.基于径向基过程神经网络的油田开发指标预测[J].计算技术与自动化,2015，34(3):52-54.

[8] 张亚光.基于云变换的信息融合方法及智能推理模型的研究[D].大庆:东北石油大学,2014.

[9] 陈惟昌,王自强,陈志华,等.神经信息学的原理与展望[J].生物物理学报，2001，17(4):613-620.

[10] 吴雅娟,许少华.一种模糊计算过程神经元网络及其应用[J].东北林业大学学报,2008,36(8):43-44.

[11] Shang L,Liu G,Zhang R,et al.An information fusion algorithm for integrated autonomous orbit determination of navigation satellites[J].Acta Astronautica,2013,85(4):33-40.

[12] 李小红.信息Agent在CSCW中的应用[D].大庆:东北石油大学，2006．

[13] 许少华,张亚光,李学贵.一种基于逆向云变换的混合推理神经网络[J].计算机技术与发展,2015,25(3):118-121.

[14] Pavlin G,Oude P D,Maris M,et al.A multi-agent systems approach to distributed Bayesian information fusion[J].Information Fusion,2010,11(3):267-282.

[15] 李盼池,许少华.加权模糊推理网络及在水淹层识别中的应用[J].计算机应用,2004,24(10):105-107.

[16] Tiruneh A T.Higher order aitken extrapolation with application to converging and diverging gauss-seidel iterations[J].Journal of Applied Mathematics & Physics,2013,5(11):128-143.

[17] 衣治安,牟春苗,孙寅萍.基于改进粒子群算法的模糊神经网络[J].计算机系统应用,2014,23(6):135-140.

[18] 董焕忠.基于加权模糊推理网络的河流-三角洲储层沉积微相识别[J].大庆石油学院学报，2005,29(1):24-27.

[19] 裴琴娟.解线性方程组的共轭梯度法[J].新乡学院学报:自然科学版,2011,28(4):309-310.

[20] 王金海,丁 锋.CARMA模型离线最小二乘迭代辨识方法[J].科学技术与工程,2007,7(23):5998-6003.

[21] 徐士良.计算机常用算法[M].第2版.北京:清华大学出版社,1995:95-101.

[22] Messaoudi S,Messaoudi K,Dagtas S.Bayesian data fusion for smart environments with heterogenous sensors[J].Journal of Computing Sciences in Colleges,2010,25(5):140-146.

Pattern Recognition of Sedimentary Microfacies with Fuzzy Inference Process Neural Network

LIU Ling-yun1，XU Shao-hua1,2

(1.College of Computer and Information Technology,Northeast Petroleum University,Daqing 163000,China;2.College of Information Science and Engineering,Shandong University of Science and Technology,Qingdao 266000,China)

So far,the static quantitative data of well logging curves have been mostly used to identify the sedimentary microfacies in the existing oil fields,which is difficult to reflect the influence of logging depth accumulation on pattern recognition of sedimentary microfacies.Taken into the above shortcomings account,a discriminant model combining fuzzy inference and process neural network is established and proposed to realize the judgment of sedimentary microfacies,on the basis of selection of information on quantitative and qualitative mixing process in the logging curve,which has been quantitatively processed to simplify the discriminant rule and extract the valid discriminant data so as to improve the accuracy of the sedimentary microfacies discrimination.Considered that the logging data is characteristic of the curve with depth the advantage in process input of the process neural network is introduced and then accuracy of sedimentary microfacies discrimination by continuously optimizing the learning mechanism of process neural networks is improved.The experimental results show that it has high accuracy and high rate,which is a practical method for the identification of sedimentary microfacies.

fuzzy reasoning;process neural network;learning algorithm;sedimentary microfacies discrimination

2016-04-14

：2016-08-17 < class="emphasis_bold">网络出版时间

时间：2017-07-11

黑龙江省教育科学技术研究资助项目(12541086)

刘凌云(1990-)，女，硕士，研究方向为软件工程；许少华，教授，博士生导师，研究方向为神经网络、优化算法。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1452.014.html

TP301

:A

:1673-629X(2017)09-0161-05

10.3969/j.issn.1673-629X.2017.09.035