基于迭代卡尔曼滤波的传感器数据融合仿真
2017-09-19林树靖仇三铭张同兴
韦 黔,陈 迪,林树靖,仇三铭,张同兴
(1.上海交通大学 电子信息与电气工程学院 仪器科学与工程系,上海 200240;2.上海智能诊疗仪器工程技术研究中心,上海 200240;3.上海直川电子科技有限公司,上海 201109)
基于迭代卡尔曼滤波的传感器数据融合仿真
韦 黔1,2,陈 迪1,2,林树靖1,2,仇三铭1,2,张同兴3
(1.上海交通大学 电子信息与电气工程学院 仪器科学与工程系,上海 200240;2.上海智能诊疗仪器工程技术研究中心,上海 200240;3.上海直川电子科技有限公司,上海 201109)
在对运动系统进行实时动态姿态信息检测过程中,常常需要加速度计、陀螺仪等多个惯性传感器的协同工作,因此需要对多传感器的输出数据进行融合处理。卡尔曼滤波法是其中常用的一种数据融合算法。该算法的滤波融合精度,直接影响了运动系统姿态信息的精度与实时性。在研究传统的卡尔曼滤波算法的基础上,仿真分析了过程噪声协方差矩阵、测量噪声协方差矩阵对于卡尔曼滤波算法的滤波精度、响应时间的影响,提出了一种基于数据迭代法的卡尔曼滤波融合算法。该算法将多传感器数据融合后的输出再次进行迭代运算,实现了较好的融合效果。仿真实验结果表明,相较于传统的卡尔曼滤波算法,所提出算法的复杂度低,实时性好,同时滤波精度大幅提升。
卡尔曼滤波器;传感器数据融合;滤波精度;迭代法;仿真
0 引 言
在如设备安装、机器人控制、测量机床仪器导轨的直线度、小车的位姿控制等领域中,都经常需要测量倾角。但是目前市面上的倾角传感器大多价格昂贵,因此该类型传感器的应用受到了一定限制。而且通常的倾角传感器主要用于静态测量,测量精度易受物体运动加速度的影响,导致测量误差增加,甚至无法使用。虽然国外如XSENS等公司已有类似产品上市[1],但价格居高不下,而且精度不高,使其应用范围受限。虽然也有高精度的军民两用产品(如美国Crossbow的产品)[2],但其高昂的价格同样令国内厂家无法承受,另有部分产品由于其高指标而不能顺利购买。就国内而言,目前还没有类似的研发成熟、成本低廉、精度较高的产品用于实际的工业与科研领域,因此进行动态倾角传感器的自主研发与生产,不仅可以打破国外的垄断,而且具有广阔的市场前景与巨大的经济价值。
在动态倾角传感器的设计过程中,关键的问题在于通过卡尔曼滤波器对采集到的加速度计信号与陀螺仪信号进行数据融合,以获得高精度、稳定的输出角度值[3-5]。由于目前国内外研究者对卡尔曼滤波器相关参数的选取仍然缺乏成熟、有效的方法,因此往往因参数选取不当,造成滤波精度较低,甚至出现滤波发散等情况[6]。通过Matlab软件建立仿真模型,在分析过程噪声协方差矩阵、测量噪声协方差矩阵对传统卡尔曼滤波算法的滤波精度、响应时间的影响的基础上,提出一种基于数据迭代法的卡尔曼滤波融合算法,将多传感器数据融合后的输出再次进行迭代运算,并与传统卡尔曼滤波算法进行仿真对比。
1 卡尔曼滤波数据融合算法
卡尔曼滤波法于1960年由匈牙利数学家卡尔曼提出[7],经过数十年发展,如今广泛应用于导航与定位、图像识别、传感器数据融合等多个领域[8-9],并衍生出了多种创新算法。该算法主要包括两个过程:预估与校正。首先通过预估过程,建立时间更新方程来对当前系统的状态进行一个先验估计,及时向前推算当前状态变量和误差协方差估计的值,以便为下一个时间状态构造先验估计值;然后校正过程负责反馈,利用测量更新方程在预估过程的先验估计值及当前测量变量的基础上,建立起对当前状态改进的后验估计。这个过程称之为预估-校正过程,对应的估计算法称为预估-校正算法[10-14]。将系统的倾角真值与陀螺仪的常值偏差b作为状态向量,用于加速度计与陀螺仪数据融合的离散卡尔曼滤波方程如下所示:
(1)
(2)
(3)

(4)
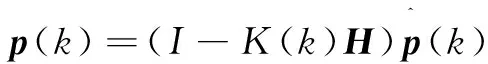
(5)
其中,A为系统状态变换矩阵;H为系统观测模型矩阵;p(k)为系统估计误差协方差矩阵;K(k)为卡尔曼增益或混合因数;R为系统测量误差协方差矩阵;ωgyro为陀螺仪的输出值;φacce为加速度计的输出值;T为采样时间;Q为系统过程噪声协方差矩阵,其具体形式为:
(6)
其中,qacce与qgyro分别为加速度计与陀螺仪的测量误差。
通过上述五个卡尔曼滤波方程的反复迭代计算,可以将加速度计输出的角度值与陀螺仪输出的角速度值进行融合,找到系统的最佳输出,得到一个高精度的物体姿态角度值。
2 仿真实验
为了验证滤波算法取不同参数对于卡尔曼滤波特性的影响,通过数据采集装置采集了动态倾角传感器在施加外部扰动情况下的输出角度值并利用Matlab软件进行仿真实验。
2.1数据采集装置结构
数据采集装置由倾角传感器、串行接口与电子计算机组成。其中倾角传感器由一个加速度计ADXL203、两个正交放置的陀螺仪ENC-03R、电源模块以及STM32单片机模块组成。加速度计测量得到的物体角度值与陀螺仪测量得到的物体角速度值经过串行接口进入电子计算机进行保存,然后通过Matlab软件进行仿真。
2.2仿真实验过程
(1)调试数据采集装置;
(2)将倾角传感器水平放置于实验台,开始供电,一段时间后开始采样。在采样过程中,对传感器施加两段小幅扰动,同时在两段扰动中间让传感器有一个小幅的角度变化(10°);
(3)结束采样,分别保存采集到的物体角度与角度值数据,送入Matlab,进行卡尔曼滤波数据仿真实验;
(4)改变卡尔曼滤波器参数,重复上述仿真过程,对结果进行对比。
3 实验结果
设置采样间隔为0.02 s,采样时间为6.68 s,在开始数据采集后的1.7~2.4 s之间施加一段扰动,然后从2.9 s开始给予系统一个角度变化,直到3.4 s后恢复稳定,最后从4.4 s开始施加第二段扰动。将系统角度值突变后的滤波响应时间t(从采样时间2.9 s处角度值开始突变到角度值回到稳态值的90%的时间)、超调量(角度值跳变后的第一个波峰减去稳态值)与第二段扰动进行滤波后的输出角度误差平均幅值作为评价滤波效果的指标。采集到的加速度计输出如图1所示。

图1 加速度计输出角度采样值
加速度计的测量值指标如表1所示。

表1 加速度计测量数据采集指标
3.1Q阵对于滤波效果的影响
假设对于加速度计输出与陀螺仪输出的信任度相等,即qacce=qgyro,则Q阵可量化为一个常数a与二阶单位阵I的乘积,即:Q=a*I。保持其他参数不变,取R=10-3,变化测量噪声协方差矩阵Q的初值,对采样数据进行卡尔曼滤波,得到的不同滤波效果如图2所示。
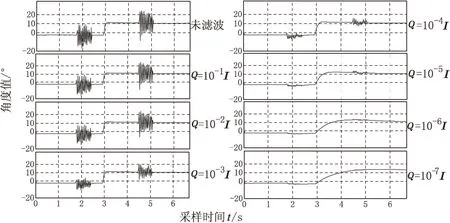
图2 不同Q取值下的卡尔曼滤波效果
由图2可见,随着过程噪声协方差矩阵Q逐渐减小,滤波后的误差平均幅值逐渐降低,但是Q进一步减小到10-4以后,滤波后的角度值会产生超调,且随着Q的进一步减小,超调会有一定的增大。与此同时,系统对角度值突变的跟踪速度变慢了,需要一定时间才能跟踪出角度的变化,即响应时间越来越长。
3.2R阵对于滤波效果的影响
为了进一步研究R的取值对于滤波效果的影响,综合考虑响应时间、超调量与误差平均幅值的影响,取Q=10-3I,保持其他参数不变,改变R的初值,不同取值情况下的滤波效果如图3所示。
从图3可以看出,R取值较大时滤波效果较好,对误差的抑制效果较大。但是会产生超调,且响应较慢。如果继续减小R,对于误差的抑制作用将越来越低,但无超调,跟踪速度较快。
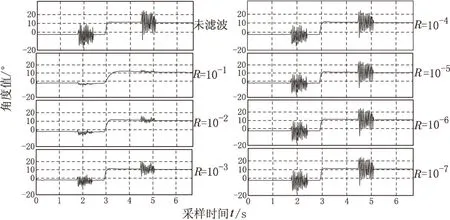
图3 不同R取值下的卡尔曼滤波效果图
4 引入迭代法的卡尔曼滤波仿真
通过对Q和R的讨论,发现无法得到一个能使卡尔曼滤波器获得最优滤波效果的Q、R取值,使其同时满足响应快、滤波精度高的要求。实际上,对于Q、R参数的最优化选取一直是卡尔曼滤波领域一个亟待解决的问题。为了克服这一问题,通过在卡尔曼滤波器中引入迭代法来进行滤波。选择一个固定的Q、R取值(Q=10-3I,R=10-3),采用已滤波后的输出信号作为新的输入信号再次进行滤波,得到一个新的输出信号,将这样的一次再滤波过程称为一次迭代滤波过程,经过一次迭代滤波后的输出信号称为一次迭代滤波信号。同理,经过多次迭代滤波后的输出信号称为多次迭代滤波输出信号。通过Matlab仿真,可将不同迭代次数下原始信号经卡尔曼滤波后的滤波效果在图4与图5中加以比较。

图4 不同迭代次数下的卡尔曼滤波效果图
从不同迭代次数下的滤波效果可以看出,采用迭代法卡尔曼滤波进行数据融合,与未迭代相比滤波效果有所提升,而且随着迭代次数的增加,滤波后的误差平均幅值与未迭代相比有大幅减少,但也注意到,当迭代次数过多时,误差平均幅值的减小将不再明显。与此同时,系统会开始产生超调,同时超调量会随着迭代次数的增加越来越大,同时响应越来越慢。迭代3次情况下实时性好,滤波精度高,超调也较低。

图5 不同迭代次数下的卡尔曼滤波效果指标对比
5 结束语
相关参数的选取问题一直是影响传统卡尔曼滤波算法滤波效果的关键因素,而目前还没有成熟、有效的取值方法,通过采用Matlab软件对采集到的倾角传感器输出数据进行仿真并具体量化分析比较Q、R两个关键参数的不同取值对卡尔曼滤波性能所造成的影响,在此基础上进行分析比对,找到了一个较优的取值组合。为了进一步提高滤波效果,在传统卡尔曼滤波算法的基础上,提出了迭代法卡尔曼滤波,将一次卡尔曼滤波后的输出数据再次引入系统进行迭代融合滤波。
仿真结果表明,在恰当的迭代次数条件下(3次),相较于传统的卡尔曼滤波法,该算法可大幅提高系统的滤波精度,使低滤波后误差的平均幅值,同时保证了系统的实时性,具有一定的工程应用价值。
[1] Giansanti D,Maccioni G,Macellari V.The development and test of a device for the Reconstruction of 3-D position and orientation by means of a kinematic sensor assembly with rate gyroscopes and accelerometers[J].IEEE Transactions on Biomedical Engineering,2005,52(7):1271-1277.
[2] Tiwari A,Ballal P,Lewis F L.Energy-efficient wireless sensor network design and implementation for condition-based maintenance[J].ACM Transactions on Sensor Networks,2007,3(1):1.
[3] 冯智勇,曾 瀚,张 力,等.基于陀螺仪及加速度计信号融合的姿态角度测量[J].西南师范大学学报:自然科学版,2011,36(4):137-141.
[4] 邹 波,张 华,姜 军.多传感信息融合的改进扩展卡尔曼滤波定姿[J].计算机应用研究,2014,31(4):1035-1038.
[5] 高同跃,龚振邦,罗 均,等.基于加速度计和角速率陀螺的超小无人直升机姿态控制系统[J].飞行器测控学报,2007,26(1):70-73.
[6] Kownacki C.Optimization approach to adapt Kalman filters for the real-time application of accelerometer and gyroscope signal’s filtering[J].Digital Signal Processing,2011,21(1):131-140.
[7] Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of Fluids Engineering,1960,82(1):35-45.
[8] 钟伟才,刘 静,刘 芳,等.二阶卡尔曼滤波分布估计算法[J].计算机学报,2004,27(9):1272-1277.
[9] 夏伟才,曾致远.一种基于卡尔曼滤波的背景更新算法[J].计算机技术与发展,2007,17(10):134-136.
[10] 梁丁文,袁 磊,蔡之华,等.基于无迹卡尔曼滤波传感器信息融合的车辆导航算法[J].计算机应用,2013,33(12):3444-3448.
[11] 周战馨,高亚楠,陈家斌,等.基于无轨迹卡尔曼滤波的大失准角INS初始对准[J].系统仿真学报,2006,18(1):173-175.
[12] 董健康,安 东.自适应卡尔曼滤波在组合导航中的应用研究[J].计算机技术与发展,2011,21(10):183-185.
[13] Gan Q,Harris C J.Comparison of two measurement fusion methods for Kalman filter based multisensor data fusion[J].IEEE Transactions on Aerospace and Electronic Systems,2001,37(1):273-279.
[14] 卞月根,张 伟.基于非线性卡尔曼滤波的车辆定位优化算法[J].计算机技术与发展,2015,25(8):80-83.
Simulation of Multisensor Data Fusion Based on Iterative Kalman Filter
WEI Qian1,2,CHEN Di1,2,LIN Shu-jing1,2,QIU San-ming1,2,ZHANG Tong-xing3
(1.Department of Instrument Science and Engineering,School of Electronic Information and Electrical Engineering,Shanghai Jiaotong University,Shanghai 200240,China; 2.Shanghai Engineering Research Center for Intelligent Diagnosis and Treatment Instrument,Shanghai 200240,China; 3.Shanghai Zhichuan Electronic Tech Co,Ltd.,Shanghai 201109,China)
It is needed the cooperation for inertial sensors like accelerometers and gyroscopes in real-time and dynamic attitude information detection for mobile system,so the output data of multisensors is required to fuse and process.The Kalman filter,as a data fusion algorithm,is usually adopted and its filtering accuracy would have a direct influence on the accuracy and real-time performance of the attitude information of mobile system.On the basis of research on the traditional Kalman filter,simulation and analysis of the impact of process and measurement noise covariance matrix on the accuracy and response time of Kalman filtering algorithm,a novel Kalman filter based on a data iterative algorithm is presented,which carries on the iterative operation again for the output after fusion of multisensors data,realizing the good effect.Simulation shows that it has a good real-time performance and low complexity and promotes filtering accuracy significantly compared with traditional Kalman filter.
Kalman filter;sensory data fusion;filtering precision;iterative algorithm;simulation
2016-09-06
:2016-12-14 < class="emphasis_bold">网络出版时间
时间:2017-07-05
科技部重点研发项目(2016YFC0100902);上海市闵行区产学研项目(2014MH163)
韦 黔(1991-),男(布依族),硕士研究生,研究方向为MEMS传感器;陈 迪,教授,博士生导师,研究方向为非硅MEMS微加工技术、准LIGA技术、Bio-MEMS和RF-MEMS。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1651.052.html
TP301.6
:A
:1673-629X(2017)09-0137-04
10.3969/j.issn.1673-629X.2017.09.030
