在线社交网络的双谣言模型研究
2017-09-19付明明余莎莎应志领
付明明,余莎莎,应志领
(南京邮电大学 理学院,江苏 南京 210023)
在线社交网络的双谣言模型研究
付明明,余莎莎,应志领
(南京邮电大学 理学院,江苏 南京 210023)
为更好地反映在线社交网络中多则谣言的传播过程,在研究两则相关谣言在社交网络传播过程中相互作用的基础上,基于在线社交网络拓扑模型和经典的传染病模型,提出并建立了两则相关性谣言在社交网络中传播的SIR模型,为研究多则谣言在网络中的传播过程提供了基础模型。为验证所提出模型的有效性和可行性,针对社交网络的小世界和无标度特性,基于所构建的人工网络进行了数值仿真验证,对比分析了基本再生数在两则谣言传播模型中对谣言扩散的影响。仿真实验结果表明,相对于较小的社交网络,谣言在无标度网络中具有更快的传播速度与更大的扩散规模;互动因子取值越小,一则谣言的扩散将抑制另一则谣言的传播,但随着互动因子的增加,这种抑制作用逐渐减弱。所提出的双则谣言模型,为相关职能部门在舆情监控和危机决策方面提供了有效的理论分析依据。
相关性谣言;SIR模型;社交网络;基本再生数
1 概 述
20世纪60年代,Milgram首次提出六度分离理论[1],为在线社交网络的发展奠定了理论基础。对于社交网络研究的网络科学理论源于复杂网络的研究,其相关理论可以追溯到1960年Erdös和Rényi提出的ER随机图模型[2]。在此基础上,关于复杂网络的研究发展迅速,其中最显著的成果当属Watts等(1998年)基于网络聚类性质提出的小世界网络模型[3],以及Barabési等(1999年)通过分析网络的入度和出度近似服从幂律分布提出的无标度网络模型[4]。此后,大多数学者基于以上两种网络模型,根据不同的网络拓扑特征,对模型进行修正和推广[5-6]。
近年来,社交网络发展迅速,日益增大的网络规模与不断进步的通讯技术,在方便用户日常交流,分享信息的同时,也促进了谣言、不良广告等恶意消息的传播。小到损害个人名誉,带来精神困扰;大到影响社会稳定,给国家治安带来潜在威胁,谣言的危害无处不在[7]。如何识别谣言,抑制谣言,预防谣言,对净化网络环境,提高社会安定具有深刻意义。同时,由于在线社交网络已经为当今谣言扩散的最大媒介,对于谣言传播的研究不再仅仅局限于社会传媒领域,来自于网络、社会学、数学、生物学等跨领域学者的合作,为研究谣言传播机制带来了全新的视野。张鹏等基于认知过程,采用Hayashi数量化理论,对网络谣言的种类进行划分[8];余莎莎等建立了传染病模型,描述商业谣言扩散造成的损失,并利用优化函数,对雇佣网络推手辟谣的成本收益进行评估[9];毛二松等根据微博感情倾向,传播过程和历史信息抽取其深层特征,进行谣言检测[10]。主要针对谣言传播过程进行建模分析,构建谣言扩散的数学模型,分析其潜在的传播特征和动力学性质。
关于谣言传播模型的研究可以追溯到1964年Daley和Kendall根据网络中谣言扩散与病毒传播的相似性,首次提出的D-K模型[11]。在此基础上,越来越多的学者根据生物病毒网络中病毒传播的特征,建立谣言传播模型:Xia等基于用户在决策谣言传播过程中的犹豫机制,提出了一个改进的SEIR模型[12];Zhao等考虑了一种特殊情况,即健康者在接触谣言后将必然改变他们的状态,提出了一个改进的SIR模型[13];Gu等分析了谣言扩散过程中用户对于谣言的遗忘与记忆机制[14]。除此以外,针对谣言扩散过程中用户的状态,谣言传播机制等,学者们基于平均场理论和经典的SIR模型,也进行了相关研究[15-16]。
以上研究皆是针对网络中的单则谣言,但在现实网络中,往往是多条信息同时传播且相互之间存在影响。多则谣言同时在网络中传播也会根据彼此内容上的相关性相互影响,内容相近的谣言在传播时相互促进,而内容相悖的谣言在传播时会相互抑制。此外,许多内容上看似独立的谣言,在传播过程中却有关联。例如第一则谣言为某地区核电站发生核泄漏,核原料汇入大海,第二则谣言则为东南沿海地区民众疯狂抢购含碘食盐,显然当用户在接受第一则谣言时,针对第二则谣言,用户更有可能选择相信。以上谣言之间的相互作用被学者们称为互动作用[17]。为此,围绕两则谣言在网络中的同时传播,分别就其相互促进,相互抑制的情况进行研究,并建立了两则谣言传播的SIR模型,为今后研究多则谣言在网络中的共同传播提供了基础和参考。
2 经典模型
2.1网络拓扑模型
在线社交网络自诞生以来发展迅速,在方便大众沟通交流的同时,也带来了海量的数据,网络用户已全面步入大数据时代。社交网络中,具有类似特征(如兴趣爱好、关注热点)的用户彼此连接,构成网络拓扑。对于不同结构的网络,谣言具有不同的传播机制。顾亦然等研究了无标度网络中谣言传播演化的过程,发现了谣言在无标度网络中扩散的高速性[18];万佑红等分别在小世界和无标度网络中研究了从众效应对谣言扩散的影响[19]。因此,网络的拓扑结构对谣言传播过程具有显著的影响力。网络理论作为复杂网络理论的延伸,已经以一种全新的视角快速发展成为一个新学科[20],当下,最为常用和经典的网络模型当属WS小世界网络和BA无标度网络模型。
Watts等研究发现,在线社交网络具有显著的社区结构,即网络中的节点基于某些特征,彼此联系紧密,形成社区。社区中的节点相较社区外的节点连接更为紧密,结构也更为牢固,形成小世界。同时,大量数据表明,社交网络中用户之间的平均路径长度很小,聚类特性显著。基于以上两个特征,Watts等[3]在完全规则网络中利用随机重连算法,建立了WS小世界网络,该网络描述了社交网络的小世界特征和聚类特征。此外,利用随机化加边算法替代随机化重连,学者们还提出了NW小世界网络模型。WS小世界网络在拓扑性质上具有平均路径长度短、聚类特性显著等特点,其度分布近似服从泊松分布,聚类系数为:
(1)
其中,Ci=2Ei/ki(ki-1),ki为节点i的邻居数,Ei为节点i的ki个邻居节点之间的实际边数;N为网络规模。
小世界网络的平均路径长度具有如下形式:
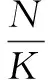
(2)
其中,K为网络平均度;p为随机重连概率;f(x)为一个与模型参数无关的普适度函数。
WS网络模型虽然合理描述了实际网络的小世界和聚类特征,但实际网络中存在少量hub节点,小度值节点大量存在的分布特征却不符合泊松分布。因此,Barabési等基于网络增长的“马太效应”建立了BA网络模型。该模型所描述的网络度分布服从幂律分布:
P(k)~k-λ
(3)
由于这类网络的节点的度没有明显的特征长度,故称为无标度网络。在此基础上,许多不同领域的网络度分布(如电力网络、蛋白质交互网络、社交网络等)都可以用适当的幂律形式较好地描述。
当下,WS小世界网络以及BA无标度网络已成为研究社交网络拓扑特征的主要模型工具。下面,将从经典传染病模型出发,研究网络中两则谣言同时扩散的情况,并在仿真分析中基于这两种模型进行研究。
2.2经典SIR模型
由于谣言扩散与病毒传播的相似性,传染病模型作为研究谣言传播的基础模型一直深受学者们的青睐。在经典的SIR模型中,用户根据所处的不同状态可划分为三类,即易感人群(susceptible individual),感染者(infected individual),免疫者(removed individual)。易感人群在网络中处于健康状态,对谣言未知且尚未接触;感染者为谣言的传播者,在网络中对谣言进行扩散;当感染者对谣言失去兴趣,或发现辟谣信息时,将对谣言产生免疫,转化为免疫者。Zhao等[13]指出在某些特殊情况下,易感人群在接触谣言后,将必然改变其自身状态,如图1所示。
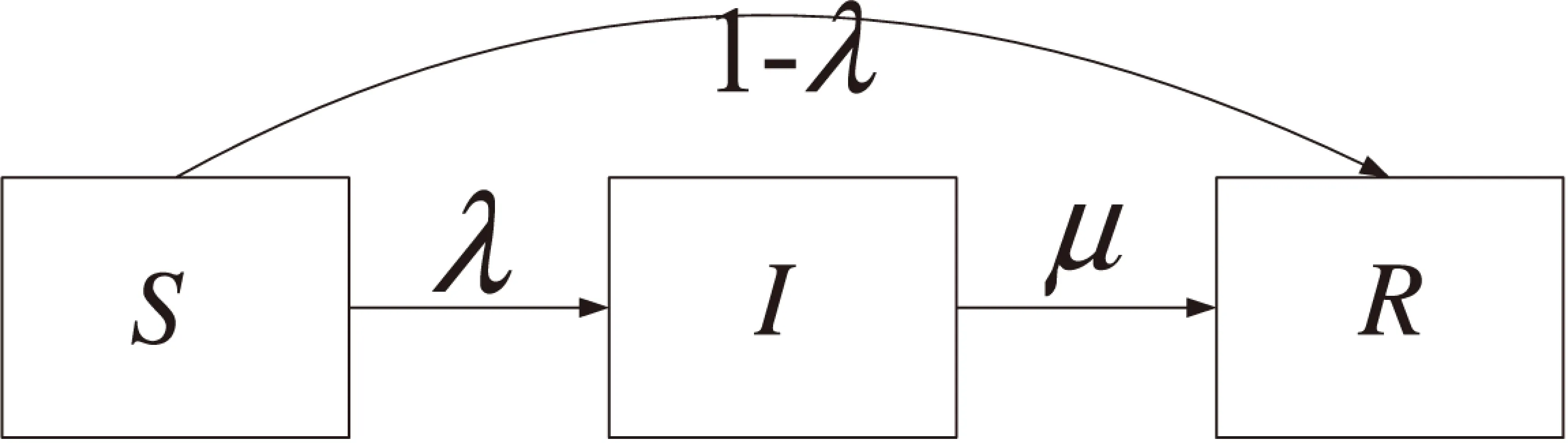
图1 经典SIR模型传播示意图
其中,λ为感染率,即用户接触谣言后选择相信谣言的概率;μ为免疫率,即感染者转变为免疫者的概率。
由图1可知,易感人群在接触谣言后,若没有转变为感染者,则必定转变为免疫者,对应在实际网络传播中用户对于谣言做出相信或不相信的情况。在社交网络中,每一时刻,用户的状态都将根据其连接状态以及邻居节点的状态发生改变,其在均匀网络中的转变过程可用以下经典SIR模型进行描述:
(4)
其中,S(t),I(t),R(t)为各个状态用户数所占比例;
此外,假定用户的生存周期要远大于谣言在网络中的生存周期,在谣言扩散过程中,用户总数不会发生改变,因此,式(4)的模型还将受到求和条件的约束:
S(t)+I(t)+R(t)=1
(5)
由以上假设可知,所研究网络的用户总数以及网络拓扑结构不会发生改变,因此所研究的对象是静态网络。
3 两则谣言扩散SIR模型
在实际社交网络中,每一时刻都伴随着多条信息的传播,且信息之间相互作用,对彼此的传播产生影响。经典的SIR谣言传播模型针对单一谣言的扩散进行研究,忽略了谣言之间的相互作用,只考虑了多条谣言传播中最简单的情况,即两则谣言同时传播,分析谣言之间的互动作用,建立两则谣言共同传播的SIR模型。
在建立模型之前,提出如下几点假设:
(1)每一个个体的状态都是对两则谣言状态的复合,如一个用户对于两则谣言均处于未知状态,则用户状态为SS,由此可分别定义SS,SI,SR,IS,II,IR,RS,RI,RR九种状态,描述网络中两则谣言的传播情况。
(2)两则谣言同时传播的过程,可拆分为用户分别对单则谣言的传播,用户的子状态对应用户对单则谣言的状态。
(3)用户对一则谣言的状态将对另一则谣言的传播产生影响,用户已知和未知一则谣言所对应的另一则谣言的感染率和免疫率不同,即用户的子状态决定了谣言扩散的过程。
根据以上假设,可做出两则谣言在网络中同时传播的示意图,如图2所示。
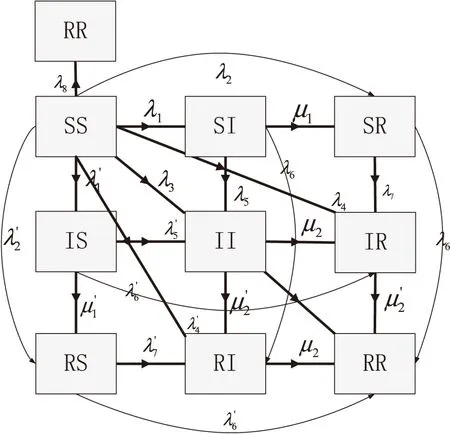
图2 两则谣言传播示意图

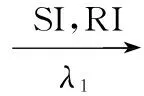
(6)
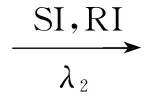
(7)
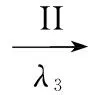
(8)
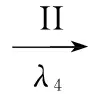
(9)

(10)
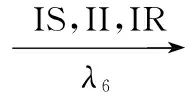
(11)
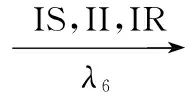
(12)
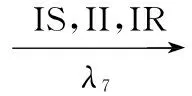
(13)
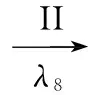
(14)
(15)
(16)
(17)
同时,由于易感人群在遭遇感染者后将不可避免地改变自身的状态,因此,可得到如下约束条件:
(18)
(19)
(20)

λ5=λ7=k1λ1,μ2=k2μ1
(21)
(22)
当k1≥1,k2≥1时,谣言2对于谣言1的扩散具有促进作用,当用户已知谣言2(处于感染态或免疫态)时,用户将有更高的概率选择相信并传播谣言1,同时,当用户对谣言2失去兴趣,或发现谣言2的辟谣时,也将加速用户免疫谣言1;反之,当k1<1,k2<1时,用户已知谣言2将对谣言1的传播起抑制作用,但会减慢用户免疫谣言1的速度。
下面,将从均匀网络的角度,给出两则谣言在网络中扩散的SIR模型。与单则谣言扩散模型相同,两则谣言在均匀网络中扩散的SIR模型也同样基于均匀混合假设[21],即一个个体与另一个个体接触的机会均等。假定ΩXX(X=S,I,R)为XX态用户人数所占比例,则根据式(6)~(17)即可得到不同状态用户人数比例随时间变化的微分方程组:
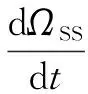
(23)
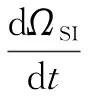
(24)
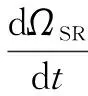
(25)
其余方程也可类比式(23)~(25)进行相应的推导,此处不再赘述。尽管两则谣言同时传播时相互影响,为简化模型,重点研究谣言2对谣言1在扩散时的影响,相应的谣言1对谣言2的传播影响也可得到类似的结论。假定ΩSX=ΩSS+ΩSI+ΩSR,则在谣言2影响下,谣言1在网络中扩散的SIR模型为:
(26)
同样,式(26)所述的模型也受到求和条件的约束:ΩSX+ΩIX+ΩRX=1,特别地当k1=k2=1,即谣言2对谣言1的传播不存在显著影响时,式(26)可以简化为:
(27)
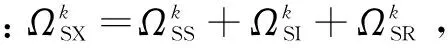
(28)
其中,P(k'|k)表示度为k的节点指向度为k'节点的条件概率。
考虑到方程的平均场特性源于忽略了网络节点之间的连接相关性,条件概率P(k'|k)可由下式得到:
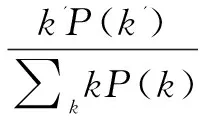
(29)
由此,基于平均场理论分别建立了均匀网络与非均匀网络中两则谣言扩散的SIR模型。
4 仿真分析
分别基于小世界网络模型和无标度网络模型进行仿真分析,就两则谣言在传播中相互抑制和相互促进进行研究,分析不同互动因子下谣言在网络中的传播特征。
采用蒙特卡洛算法进行数据仿真,为减小随机误差,所有仿真结果均由100次独立运算求数学期望取得。同时,为减弱初始节点对谣言传播的影响,每次独立运行的初始节点均不相同。此外,由于研究的重点是谣言在传播之间的相互作用,因此在谣言1与谣言2的传播过程中,假定其拥有相同的感染率与免疫率,即:
(30)
尽管状态如SI,SR的个体,对谣言2的子状态不同,但都已经接触并传播过谣言,因此假定有λ5=λ7=k1λ1;同时,对于如式(8)、(9)、(14)描述的两个子状态同时变化的转移过程,由于在前文的假设中,两个子状态变化的过程相对独立,因此两个子状态同时改变的转移过程可视为子状态1先发生改变,子状态2再发生改变(或子状态2先改变,子状态1再发生改变)的Markov过程,因此式(8)可被改写为:

(31)
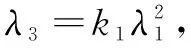
(32)
(33)
给定参数λ1,μ1以及互动因子k1,k2即可求出其余参数。
下面,利用蒙特卡洛算法,分别在网络规模N=5000,平均度
图3展示了谣言1在谣言2影响下,分别在小世界网络与无标度网络中的扩散过程。其中,λ1=0.5,μ1=1,互动因子k1=k2=0.7,即两则谣言相互冲突,谣言2对谣言1的传播起抑制作用。
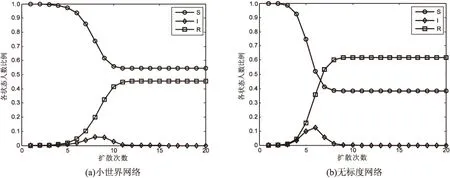
图3 在谣言抑制作用影响下,谣言在人工网络中的扩散过程
如图3(a)所示,在小世界网络中,易感人群用户比例随着谣言的扩散不断下降,而免疫者用户比例不断上升,最终趋于稳定。而感染者用户比例随着谣言扩散先增后减,存在峰值,此时谣言在网络中的扩散速度达到最大,此后,谣言虽仍在网络中传播,但感染者人数比例以及扩散速度不断下降,最终感染者人数变为0即谣言不再扩散,整个网络系统达到稳态。图3(b)为各状态用户比例随谣言扩散变化的过程。图3(b)中各曲线变化与图3(a)具有相同的趋势,随着时间的推移,谣言最终都将在网络中消失,此时系统达到稳态,各状态用户比例不再改变。对比小世界网络和无标度网络模型中的谣言扩散过程,在无标度网络中,谣言扩散速度更快,感染者的用户比例达到峰值所需的扩散次数更少,峰值更大,同时,谣言在无标度网络中的扩散规模也相对更大,稳态时相较小世界网络,免疫者人数比例更高,易感人群的比例更小。无标度网络的无标度特性以及hub节点的存在造成了以上的不同,一旦谣言感染了hub节点,其邻居节点都将收到谣言信息,加速了谣言的传播。以上仿真结果在文献[23]也得到了证实。由于实际网络中,节点分布的非均匀性以及hub节点的存在性,在描述在线社交网络时,BS无标度网络备受学者们的青睐,因此,将重点研究无标度网络中,不同互动因子对于谣言扩散的影响。
图4展示了无标度网络中,不同互动因子下,谣言1在谣言2影响下的传播过程。其中互动因子分别为k1=k2=0,0.7,1,2,模型参数λ1=0.5,μ1=1。
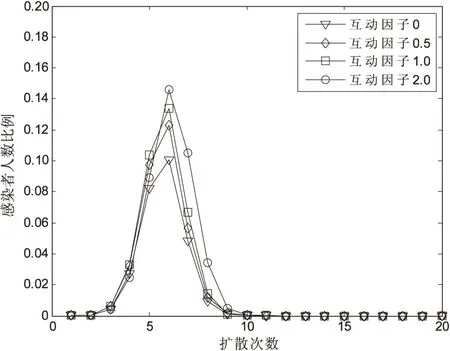
图4 无标度网络中不同互动因子下的谣言扩散过程
如图4所示,随着互动因子取值的不断增大,谣言扩散过程发生改变,谣言扩散速度提升显著,最终扩散规模也随之增大。当k1=k2=0时,谣言2完全阻碍谣言1的传播,即接触并传播谣言2的用户,将不会传播谣言1,此时谣言扩散缓慢,扩散规模也较小,随着k1,k2取值增大,谣言之间的抑制作用减小,当k1=k2=1时,两则谣言的扩散过程相互独立,传播时没有互动作用。当k1,k2取值大于1时,谣言对彼此的传播起促进作用,谣言扩散速度与扩散规模增大。
5 结束语
为更好地反映在线社交网络中多则谣言的传播过程,在研究两则相关谣言在社交网络传播过程中相互作用的基础上,基于在线社交网络拓扑模型和经典的传染病模型,提出并建立了两则相关性谣言在社交网络中传播的SIR模型。对于两则谣言的扩散过程,该模型通过分析其互动因子的取值,确定其在传播过程中相互抑制、独立或相互促进的关系,利用子状态描述个体分别对两则谣言的状态,并利用子状态转移方程表示用户个体状态的变化;将两个子状态同时改变的过程假定为在时间上子状态接连改变的Markov过程,从而给出均匀网络与非均匀网络中两则谣言同时扩散的SIR模型。基于小世界网络模型与无标度网络模型,对两则谣言同时扩散的过程在人工网络上进行仿真分析。仿真结果表明,相较小世界网络,在无标度网络中其余谣言的影响下,谣言具有更快的传播速度与更大的扩散规模,与单则谣言的传播结论相同。此外,还分析了互动因子取值对谣言传播的影响。实验结果表明,当互动因子取值小于1时,谣言之间的互动起抑制作用,特别地,当互动因子为0时,一则谣言的扩散将完全阻止另一则谣言的传播,随着互动因子不断增大,抑制作用减弱,当互动因子为1时,两则谣言的扩散过程相互独立,当互动因子大于1时,一则谣言的传播将加快另一则谣言的扩散速度并增大其扩散规模。基于现实网络中多则谣言同时扩散的情况,建立了两则谣言的扩散模型,讨论谣言之间的互动作用及其造成的影响。相较单则谣言的传播模型,考虑了更为实际的传播情况,分析了谣言之间互动作用对其动力学性质的影响,为研究多条信息同时扩散提供了基础模型,在舆情监控、网络安全领域具有一定的研究意义。
[1] Travers J,Milgram S.An experimental study of the small world problem[J].Sociometry,1969,32(4):425-443.
[2] Erdös P,Rényi A.On the evolution of random graphs[M]//Publication of the mathematical institute of the hungarian academy of sciences.[s.l.]:[s.n.],1960:17-61.
[3] Watts D J,Strogatz S H.Collective dynamics of ‘small-wo-rld’ networks[J].Nature,1998,393(6684):440-442.
[4] Barabási A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.
[5] Wang J,Zhao L,Huang R. 2SI2R rumor spreading model in homogeneous networks[J].Physica A Statistical Mechanics & Its Applications,2014,413:153-161.
[6] Zan Y,Wu J,Li P,et al.SICR rumor spreading model in complex networks:counterattack and self-resistance[J].Physica A Statistical Mechanics & Its Applications,2014,405:159-170.
[7] 柴艳茹.网络谣言对社会稳定的危害及其治理[J].人民论坛,2013(20):20-23.
[8] 张 鹏,兰月新,李昊青,等.基于认知过程的网络谣言综合分类方法研究[J].图书与情报,2016(4):8-15.
[9] 余莎莎,王友国,朱 亮.基于SIR社交网络中商业谣言传播研究[J].计算机技术与发展,2016,26(11):195-199.
[10] 毛二松,陈 刚,刘 欣,等.基于深层特征和集成分类器的微博谣言检测研究[J].计算机应用研究,2016,33(11):3369-3373.
[11] Daley D J,Kendall D G.Epidemics and rumours[J].Nature,1964,204(4963):1118.
[12] Xia L L,Jiang G P,Song B,et al.Rumor spreading model considering hesitating mechanism in complex social networks[J].Physica A Statistical Mechanics & Its Applications,2015,437:295-303.
[13] Zhao L,Cui H,Qiu X,et al.SIR rumor spreading model in the new media age[J].Physica A Statistical Mechanics & Its Applications,2013,392(4):995-1003.
[14] Gu J,Li W,Cai X.The effect of the forget-remember mechanism on spreading[J].European Physical Journal B,2008,62(2):247-255.
[15] Zhao L,Wang J,Chen Y,et al.SIHR rumor spreading model in social networks[J].Physica A Statistical Mechanics & Its Applications,2012,391(7):2444-2453.
[16] Wang J,Zhao L,Huang R.SIRaRu rumor spreading model in complex networks[J].Physica A Statistical Mechanics & Its Applications,2014,398(15):43-55.
[17] Jie R,Qiao J,Xu G,et al.A study on the interaction between two rumors in homogeneous complex networks under symmetric conditions[J].Physica A Statistical Mechanics & Its Applications,2016,454:129-142.
[18] 顾亦然,沈 贤.无标度网络中谣言传播的研究[J].计算机技术与发展,2013,23(8):254-257.
[19] 万佑红,王小初.考虑从众效应的谣言传播模型[J].计算机应用,2016,36(9):2381-2385.
[20] 汪小帆,李 翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012.
[21] Anderson R M,May R M,Anderson B.Infectious diseases of humans:dynamics and control[M].Oxford:Oxford University Press,1992.
[22] Moreno Y, Pastor-Satorras R, Vespignani A.Epidemic outbreaks in complex heterogeneous networks[J].The European Physical Journal B-Condensed Matter and Complex Systems,2002,26(4):521-529.
[23] Nekovee M,Moreno Y,Bianconi G,et al.Theory of rumour spreading in complex social networks[J].Physica A:Statistical Mechanics and Its Applications,2007,374(1):457-470.
第十五届全国嵌入式系统学术会议将在辽宁省沈阳市隆重举办
第十五届全国嵌入式系统学术会议将于2017年11月17日-19日在辽宁省沈阳市举办。会议由中国计算机学会(CCF)主办,CCF嵌入式系统专业委员会、东北大学计算机科学与工程学院、东北大学智慧系统国际创新实验室等联合承办。
本次大会将邀请院士和国内外嵌入式系统领域的顶级专家、学者作大会特邀报告,同时还设有专题论坛和分会场口头报告,科技成果展示、学术论文交流等形式多样的活动。会议旨在讨论嵌入式系统领域的最新研究成果和发展趋势,开展广泛的学术交流和研讨。欢迎从事嵌入式系统及相关领域的专家、学者、工程师、业界人士、研究生踊跃投稿并参加会议。
会议编号:CCF-17-TC16-01N
联系人:王 义wangyi@ise.neu.edu.cn
网 址:http://www.cse.neu.edu.cn/estc2017.html
Research on Double Rumor Model in Online Social Network
FU Ming-ming,YU Sha-sha,YING Zhi-ling
(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
To better reflect the spread process of rumors in online social networks,on the basis of study of two related rumors interaction in the process of social networks,the SIR model of two related rumors spreading in social networks is proposed and established based on the topological model of online social networks and classic infectious disease model,which provides a basic model for studying the spread of rumors on the network.In order to verify its validity and feasibility,considering the characteristics of small-world and the scale-free of network,the numerical simulation is presented in established artificial network,and the influence of the basic reproduction number on the rumor diffusion in two rumor spread models is also compared and analyzed.It is showed that compared with the small world network the rumors have been spreading faster and deeper in the scale-free network and that a rumor in spread can suppress another while value of interaction factor is smaller,however as interaction factor increases the inhibitory effect on another rumor becomes more and more weak.Therefore,it has provided effective theoretical references for public opinion monitoring and crisis decision.
correlative rumor;SIR model;social network;basic reproduction number
2016-10-19
:2017-01-20 < class="emphasis_bold">网络出版时间
时间:2017-07-11
国家自然科学基金资助项目(11226071);南京邮电大学校科研基金(NY213183)
付明明(1988-),男,硕士研究生,研究方向为信号处理理论与应用;应志领,硕士生导师,副教授,研究方向为环论和模论。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170711.1456.064.html
TP31
:A
:1673-629X(2017)09-0053-07
10.3969/j.issn.1673-629X.2017.09.012
