含光伏电站发电系统可靠性评估方法研究

杨 苏，黄俊辉，关志坚，袁 越，吴涵

（1.河海大学 可再生能源发电技术教育部工程研究中心，南京 210098；2.国网江苏省电力公司 经济技术研究院，南京 210008）

含光伏电站发电系统可靠性评估方法研究

杨 苏1，黄俊辉2，关志坚2，袁 越1，吴涵1

（1.河海大学 可再生能源发电技术教育部工程研究中心，南京 210098；2.国网江苏省电力公司 经济技术研究院，南京 210008）

在对含光伏电站的系统可靠性研究中，往往针对的是一整年的光伏及负荷数据，计算的结果也只能表征光伏发电对系统全年充裕度的综合贡献［4—10］，该可靠性评估的应用范围较窄，对实际生产指导作用有限。然而对于不同地区，其光伏出力特性必定会不相同，仅仅从全年的时间尺度，很难对光伏发电对系统可靠性的影响做精细化的研究，所以有必要研究不同季节以及日内不同时段光伏发电对系统可靠性的影响，以达到在更短的时间维度上，更加精细的考虑光伏资源特性以及负荷特性对系统可靠性的影响。而最常用的分段方法是按照季节的划分方式，即将年时间尺度划分为4个时间段，分别对应春、夏、秋、冬。然而该方法是一种模糊的、人为设定的分段，没有现实的依据，不能针对某地区的实际光伏出力特性进行具有针对性的最优分段。

综上所述，由于光伏出力同时具有季节时序特性与昼夜日周期特性，本文首先采用Fisher最优分段方法［11］，［12］，以光伏日有效出力时间长短为判据，将光伏年出力序列进行分段，基于肘点法［13］计算出符合该地区光伏出力特性的最优分段点，然后，针对每个分段点之间的时间段，利用模糊c均值聚类法（fuzzy c⁃mean algorithm,FCM）模拟光伏功率［14］，［15］,该方法能够使得光伏出力的建模更细化，最后，结合蒙特卡罗状态抽样方法［16］，模拟计算系统的可靠性指标值，对含光伏发电系统进行可靠性分析。以IEEE⁃RTS测试系统为例，验证了本文所提方法可以有效提升系统可靠性评估精度，量化分析接入光伏电站后，系统在不同时间段可靠性的变化情况，计算结果对光伏电站的并网容量规划具有重要指导意义。

1 最优分段与聚类理论概述

1.1 Fisher最优分段法

在含光伏发电系统的可靠性研究中，模拟光伏出力序列至关重要。考虑到光伏出力具有时序性，且其历史模拟数据量庞大，宜采用Fisher最优分段法对其进行时序分段，细化模拟时段，以保留光伏出力的局部时序特征。

假设{X1,X2,…,Xn}是n个有序样本，每个样本为m维向量。对该样本进行划分，记录样本的某一段为

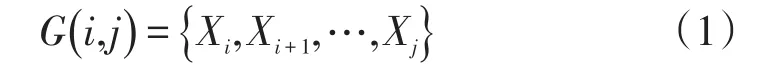
采用离差平方和作为该段直径的描述，即

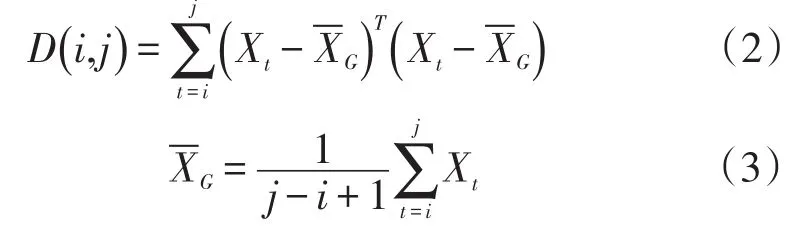
式中:D(i,j)为该有序-样本的从第i个样本到第 j个样本的离差平方和；XG为该段有序样本的均值。

在得到了每段的离差平方和时，若将该有序样本分为k段，每段的样本下标记为Bj={ij,ij+1,…,ij+k-1}，j∈{1 ,2,…,k}其中的分位点满足:1=i1＜i2＜…＜ik＜n= ik+1，从而得到总的目标函数，如公式（4）所示。

式中:L为各段的离差平方总和，L值越小，分段越合理。

对于光伏出力时间段的划分，常规的方法是按照季节进行分段，然而这一方法相对较模糊，不具有针对性，而且划分效果不够好。由Almorox和Bakirci［17］，［18］研究表明，特定地区的光照辐照度往往与该地区的日照时间呈现线性的关系。即某一时间段内，一天的日照时间长短大致的反映了辐照度强弱。而对于光伏发电系统，光伏出力又直接受到辐照度影响，所以日照时间的长短间接体现出光伏出力的强弱。基于此，本文提出一种新的分段方式，即根据一天中光伏有效出力时间长短的原则，对光伏年出力进行有序分段。

1.2 模糊c均值聚类法

FCM［14］,［15］是一种基于划分的聚类算法，最早由Bezdek在1973年提出。该算法的思想是使得被划分到同一簇的对象之间相似度最大，而不同簇之间的相似度最小。其最大的特点是应用隶属度表示数据样本属于某个聚类中心的程度，是一种柔性的模糊划分方式。

该算法的目标是使得数据集与相应聚类中心的欧式距离最小，目标函数如下

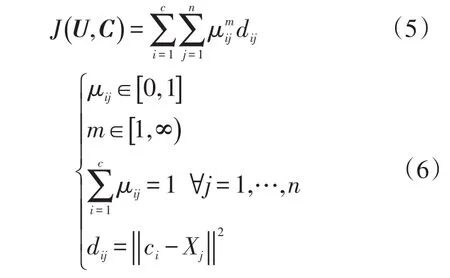
式中:U为隶属度矩阵；C为聚类中心矩阵；m为加权倍数；dij为第i个聚类中心与第 j个数据点间的欧几里得距离。

该算法是一个迭代寻优过程，可通过下面2个式子对聚类中心阵和隶属度阵进行更新

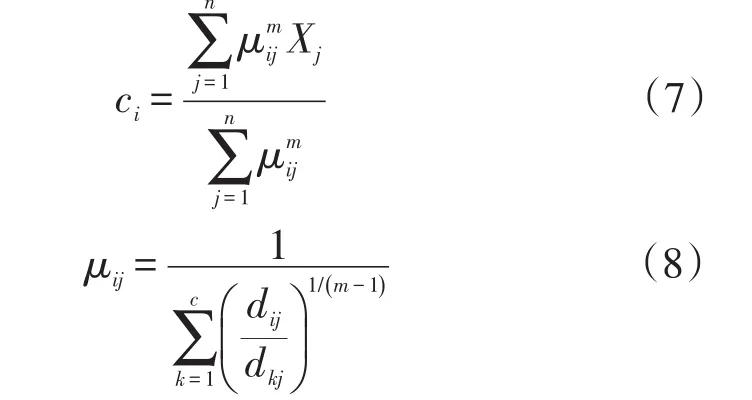
若前后2次迭代过程目标函数的改变量小于某个阈值，则聚类过程结束

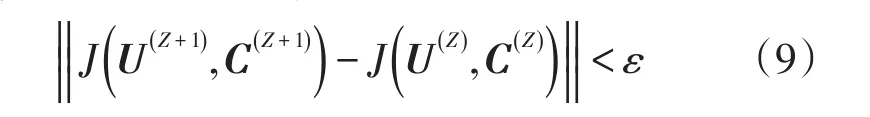
式中:J(U(Z),C(Z))为第z次迭代的目标函数值，阈值ε一般取10-4。

2 基于最优分段和多维聚类算法的可靠性评估步骤

本文首次将Fisher最优分段法和FCM方法应用在光伏出力序列的建模上，提出一种基于最优分段和多维聚类的可靠性建模方法。该方法首先对光伏出力进行时序分段处理，然后对每段进行聚类分析，抽样模拟得到系统的可靠性指标值。具体的计算步骤如下。

（1）对光伏出力序列进行重组，构成以一天24 h排列的数据方式，构成矩阵形式为365行×24列的光伏出力阵Ppv。

（2）统计得到光伏有效出力时间序列Tpv，根据光伏每天有效出力时间长短的原则，使用Fisher最优分段算法，对年模拟周期的光伏历史出力数据进行时序分段，得到最优分段点。

（3）在每个时间段，分别对光伏功率和负荷需求数据，利用FCM聚类法确定各时间段的聚类数，聚类中心和模糊隶属度阵。需要说明的是，负荷需求的聚类分析与光伏功率分析方法相同，这里不再赘述。

（4）综合以上3步得到的:各个时段光伏功率的聚类中心和模糊隶属度矩阵，各个时段负荷的聚类中心和模糊隶属度矩阵，RTS测试系统的常规机组的容量和故障率。利用蒙特卡罗状态抽样技术，规定抽样次数为105次，对每个时间段的光伏功率、负荷需求和常规机组的运行状态进行模拟，统计系统的可靠性指标。

本文采用电量不足期望［10］（lossofenergy expection, LOEE）作为可靠性指标，因为该指标不但较好的反映了系统缺电量的大小，更能反映在各个时间段内的系统可靠性。

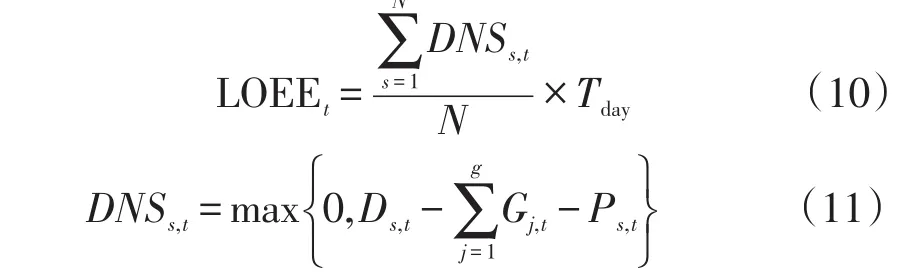
式中:s为抽样模拟中的迭代次数；t为时刻点，h；N为设定的迭代总次数；Tday为该时间段的天数；g为全部常规机组的数量；Ds,t和Ps,t分别为第s次迭代中，在时刻t的负荷需求量和光伏功率，MW。

3 算例与结果分析

本文以IEEE⁃RTS［19］测试系统作为算例，该系统含有32台发电机、系统总装机容量为3 405 MW，峰荷为2 850 MW。本文中的光伏出力数据采用宁夏某地区的光伏出力实测数据，如图1所示。（标幺值是指每个时刻的光伏出力除以全年各时刻的最大值）

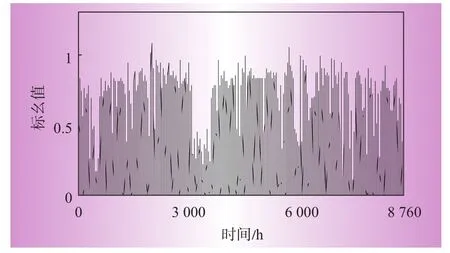
图1 光伏年出力时序列

3.1 Fisher法有效性检验

从图1可以看出，若以年为时间尺度对光伏发电系统进行可靠性分析，很难体现出该地区光伏出力的局部特征，所以本文基于日有效出力时间长短的判据，采用Fisher最优分段算法，对光伏有效出力时间序列Tpv进行有序分段，以找到最合理的分段点，分段结果如表1所示。

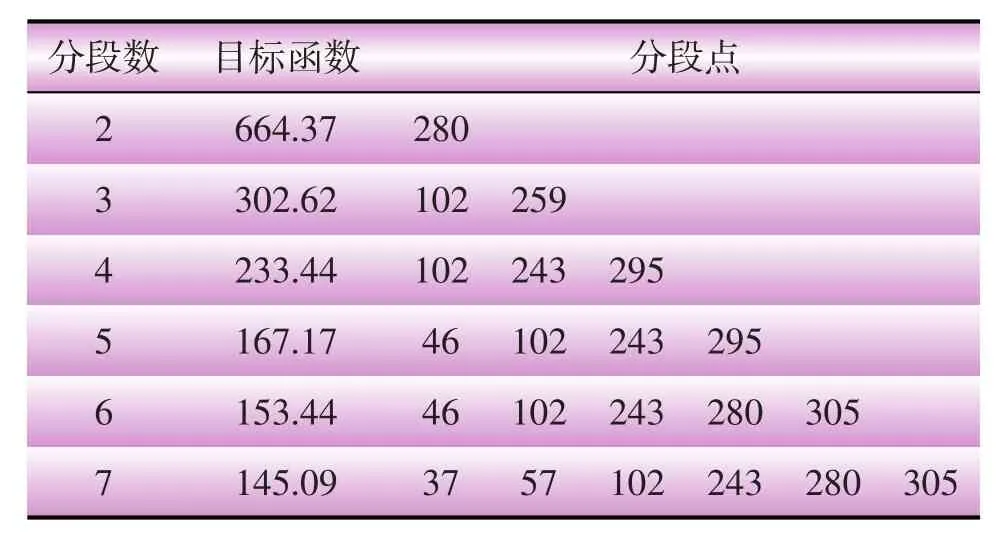
表1 Tpv有序分段结果

图2为最优分段目标函数随聚类数的变化情况。本文采用了肘点的方法确定分段数，即图中曲线的第一个拐点，即为最优分段数。从图2可以看出，当分段数达到5时，此时再增加分段数，对目标函数的改善不明显。

图2 Tpv有序分段数分析

图3为该光伏Tpv序列的杰卡德距离矩阵［20］，杰卡德距离表示2个数据之间的相似性，杰卡德距离值越小，这2个数据越相似。依据该矩阵的副对角线分布，该有序序列Tpv可以划分为5段。验证了本文Fisher最优分段方法的正确性。所以本文以5段的划分方式，对含光伏的发电系统进行时间段划分。

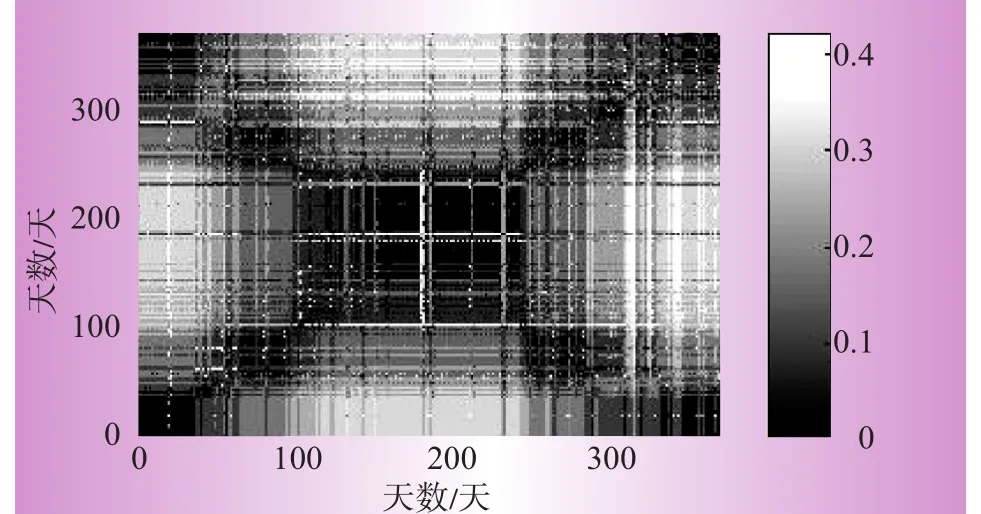
图3 Tpv的杰卡德距离矩阵

3.2 FCM法有效性检验

在使用Fisher最优分割法，将一年宁夏电网光伏出力序列划分为5个时序段后，此时需要对各段内进行细化处理分析。本文利用FCM聚类法对随机变量进行聚类分析，以模拟其随机性，如图4所示。

图4 每个时段光伏功率聚类数分析

同样采用的是肘点方法，对于时段3，随着聚类数的增加，目标函数值逐渐降低，当聚类数达到8时，此时再增加聚类数，对目标函数值的改善减弱。负荷需求的聚类分析与光伏功率分析方法相同，这里不再赘述。

如表2所示，光伏功率和负荷需求在时段3的聚类数目为8，而在其他时段都为5。这是因为光伏和负荷都具有随机性和波动性。在较长的时间段需要更多的聚类数目，以保证其模拟的精确性。

表2 光伏功率与负荷需求的聚类数目

进一步对时段3进行分析:图5和图6表示时段3内光伏功率和负荷需求的聚类结果。从图5和图6可以看出，该多维聚类方法很好的保持了随机变量具有的昼夜周期性和随机特性。

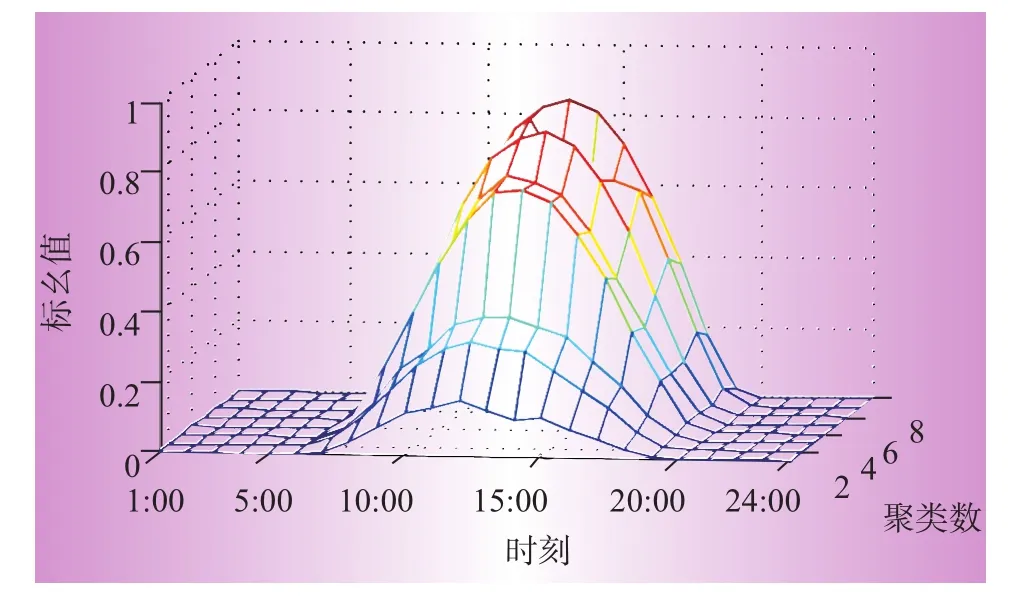
图5 光伏功率在时段3内聚类示意图

图6 负荷需求在时段3内聚类示意图

3.3 初始RTS可靠性指标检验与分析

在得到了分段点和聚类情况后，使用蒙特卡罗状态抽样技术，对初始RTS系统（此时光伏电站并未接入电网）的可靠性进行模拟分析，结果如图7所示。

图7 原始RTS各时段LOEE（电量损失期望）值

如图7所示，在未接入光伏功率时，采用本文的方法可以得到LOEE指标在各时段分布情况。为了验证本文算法有效性，将其5个时段指标值相加，得到年时段的LOEE值为1 103.24 MWh/年，文献［10］中的指标值为1 132 MWh/年，计算结果基本相符。进一步对图7进行分析:时段3和时段5分别处在夏季和冬季，负荷需求量大，这2个时段的电量损失期望占较大比重，系统可靠性较差；而在时段2和时段4，可靠性指标LOEE趋于0，此时常规机组基本能够维持系统的正常供电。进一步对各时段每个时刻点的系统可靠性分析，结果如图8所示。

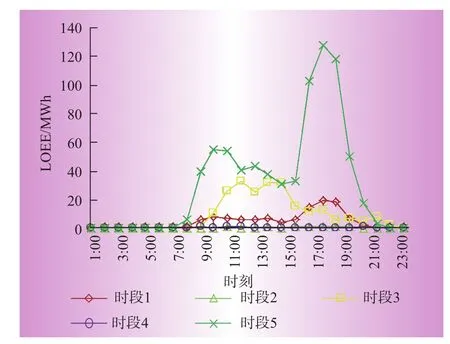
图8 原始RTS各时刻LOEE值

由图8可以看出:时段5和时段1在夜间19：00时左右达到峰值，时段3在中午13：00时达到最大值，此时的系统可靠性较差，这与夏季中午高负荷和冬季夜高负荷特性相符；时段2和时段4在各时刻点的可靠性指标值较小，说明这2个时段内系统可靠性较高，即负荷需求总体相对较小。另外，该测试系统在7：00～22：00这一时间段内，可靠性指标值LOEE大于0。说明该时间段内，系统需要添加电源供应，以保证系统安全可靠运行。比较图5可以看出，光伏具有白天发电的特性，若系统接入光伏功率，必定能够较好的改善系统可靠性。

3.4 光伏容量对系统可靠性的影响

如图9所示，随着光伏容量的增加，系统可靠性指标得到了改善，当增加的光伏容量较小时，时段3和时段5可靠性指标值下降较快。在光伏容量增加到1 800 MW时，年电量不足期望指标为456.47 MWh/年，此时系统可靠性指标值下降平缓，趋于饱和。比较图9可以看出，增加光伏功率后，时段5的曲线下降速度最快；时段1、时段2和时段4基本保持不变，引入的光伏功率对这3个时段的可靠性影响较小。

各时段的饱和情况各不相同，具体数据如表3所示。其中，时段2和时段4内由于其初始LOEE指标相对较小，接近于0，光伏容量对这2个时段的影响忽略不计。对比一年中各个时段，处在夏季的时段3相对较早的达到饱和状态，而时段5由于处在冬季，且具有较大的初始指标值，达到饱和速度最慢。这是由于本文所采用的光伏数据取自北半球，在时段3相较于时段5具有更加充沛太阳辐射，光伏功率的引入在时段3更能改善发电系统的可靠性。

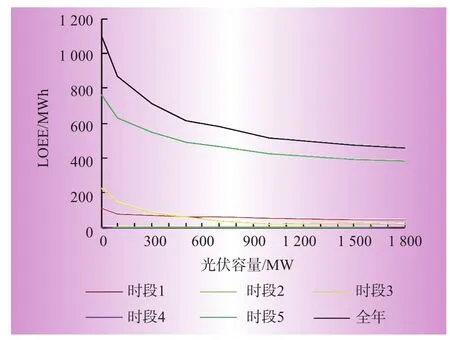
图9 各时段LOEE值随光伏容量变化

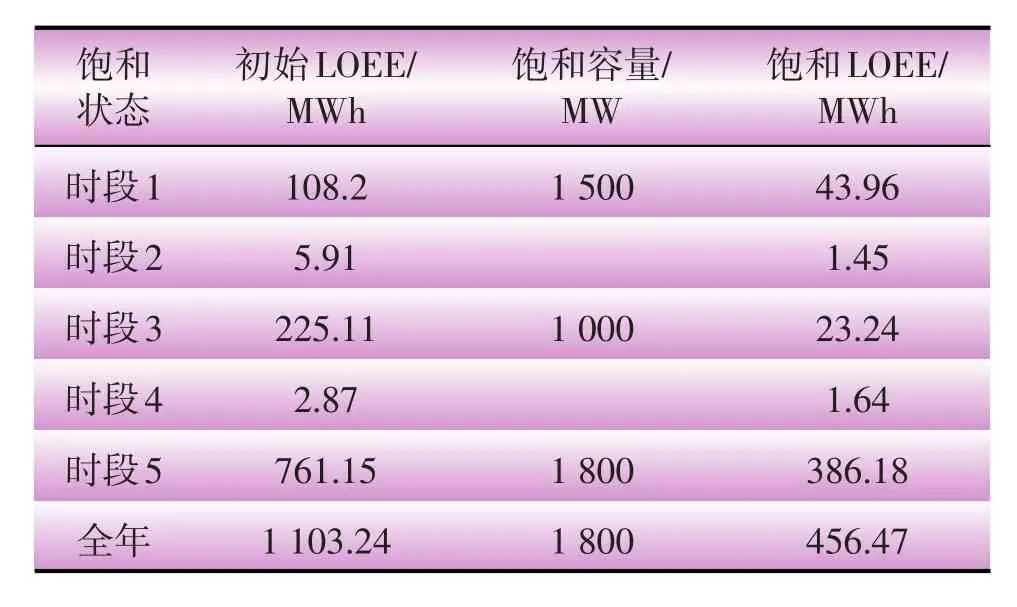
表3 各时段饱和情况对比

光伏装机容量分别为0和1 800 MW（达到饱和容量）时，RTS发电系统在各时刻点的可靠性指标值分布情况如图10所示。从图中可以看出，接入1 800 MW的光伏功率后，有效的改善了系统在白天7：00～17：00的可靠性，也验证了达到光伏容量达到1 800 MW时，其对系统可靠性的改善达到近似饱和。

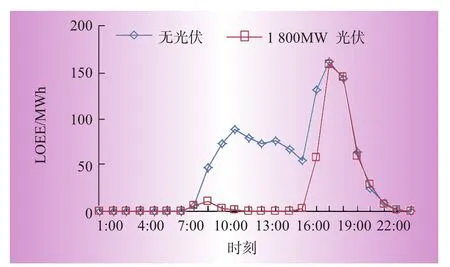
图10 全年LOEE在各时刻点分布

4 结束语

（1）本文综合考虑光伏功率具有的昼夜日周期性和季节时序周期性，提出了以光伏电站一天有效出力时间长短为判据，利用Fisher最优分段方法对光伏出力序列进行时序分段。本文得到的5段划分方式对光伏出力序列逐段精细建模，更能体现该地区光伏功率的局部时序特点，具有较强的实用性和针对性。

（2）采用FCM多维聚类算法，分别在每个时间段内，对光伏功率和负荷需求进行聚类分析，该方法简单且高效的模拟了随机变量具有的随机性和时序性的特点。

（3）以RTS测试系统作为算例，基于本文方法，模拟分析了含光伏发电的系统可靠性。比较了在每个时间段和全年这2个时间尺度上，光伏系统对发电系统可靠性的影响。即:随着光伏容量的增加，其对发电系统可靠性的贡献逐渐减小，并最终趋于饱和；同时，光伏系统对各个时间段的影响各不相同，光伏系统对时段3和时段5的可靠性改善贡献较大。本文结论可为光伏电站规划设计提供帮助。

在以后的研究工作中，需要考虑光伏电站的故障率和控制方式，并考虑不同的负荷特性，更准确分析光伏电站并网对系统可靠性的影响。D

［1］ 丁明，王伟胜，王秀丽，等.大规模光伏发电对电力系统影响综述［J］.中国电机工程学报，2014，34（1）：1-14.

［2］ Zulu E,Jayaweera D.Reliability assessment in active distribution networks with detailed effects of PV systems［J］.Journalof Modern Power Systems and Clean Energy, 2014,2（1）：59-68.

［3］ 陈炜，艾欣，吴涛，等.光伏并网发电系统对电网的影响研究综述［J］.电力自动化设备，2013，33（2）：26-32.

［4］ 王秀丽，武泽辰，曲翀.光伏发电系统可靠性分析及其置信容量计算［J］.中国电机工程学报，2014，34（1）：15-21.

［5］ 梁双，胡学浩，张东霞，等.基于随机模型的光伏发电置信容量评估方法［J］.电力系统自动化，2012，36（13）：32-37.

［6］ 王敏，宗炫君，袁越，等.含光伏电站的发电系统可靠性分析［J］.中国电机工程学报，2013，33（34）：42-49.

［7］ 丁明，徐宁舟.基于马尔可夫链的光伏发电系统输出功率短期预测方法［J］.电网技术，2011，35（1）：152-157.

［8］ 陈昌松，段善旭，殷进军.基于神经网络的光伏阵列发电预测模型的设计［J］.电工技术学报，2009，24（9）：153-158.

［9］ 代倩，段善旭，蔡涛，等.基于天气类型聚类识别的光伏系统短期无辐照度发电预测模型研究［J］.中国电机工程学报，2011，31（34）：28-35.

［10］ MOSADEGHYM,YANR,SAHAT K.Atime-dependent approach to evaluate capacity value ofwind and solar PV generation［J］.Sustainable Energy,IEEE Transactions on,2016,7（1）：129-138.

［11］ 方开泰.有序样品的一些聚类方法［J］.应用数学学报，1982，5（1）：94-101.

［12］ 贾澎涛，何华灿，刘丽，等.时间序列数据挖掘综述［J］.计算机应用研究，2007，24（11）：15-18.

［13］ KETCHEN D J,SHOOK C L.The application ofcluster analysis in strategic management research：an analysis and critique［J］.Strategic managementjournal,1996,17（6）：441-458.

［14］ MOSADEGHY M,YAN R,SAHA T K.Impact of PV penetration level on the capacity value of South Australian wind farms［J］.Renewable Energy,2016,85（7）：1 135-11 42.

［15］ GHAEDI A,ABBASPOUR A,FOTUHI-FIRUZABAD M,et al.Toward a comprehensive model of large⁃scale DFIG⁃based wind farms in adequacy assessmentofpower systems［J］.Sustainable Energy,IEEE Transactions on, 2014,5（1）：55-63.

［16］ 李文沅.电力系统风险评估:模型，方法，应用［M］.北京：科学出版社，2006：73-74.

［17］ ALMOROX J Y,HONTORIA C.Global solar radiation estimation using sunshine duration in Spain［J］.Energy Conversion and Management,2004,45（9）：1 529-1 535.

［18］ BAKIRCI K.Correlations for estimation of daily global solar radiation with hours of bright sunshine in Turkey［J］.Energy,2009,34（4）：485-501.

［19］ IEEE Reliability TestSystem Task Force of Applications of Probability Methods Subcommittee.IEEE reliability test system［J］.Power Apparatus and Systems,IEEE Transactions on,1979,98（6）：2 047-2 054.

［20］ 韩家炜，坎伯，裴健，等.数据挖掘：概念与技术［M］.北京：机械工业出版社，2 007：48-50.

（本栏责任编辑 马 雷）

Research ofreliability analysis ofgeneration systems with photovoltaic stations

YANG Su1,HUANG Jun⁃hui2,GUAN Zhi⁃jian2,YUAN Yue1,WU Han1
（1.Research Centerfor Renewable Energy Generation Engineering ofMinistry of Education,HohaiUniversity,Nanjing 210098,China;2.Economic Research Institute，State Grid Jiangsu Electric Power Company,Nanjing 210008,China;）

近年来光伏发电并网容量不断增加，如何准确评估其对发电系统可靠性的影响具有现实意义。综合考虑光伏出力具有的昼夜日周期性和季节时序特性，提出了一种基于最优分段和多维聚类算法的光伏出力建模方法。首先根据光伏每天有效出力时间长短为原则，采用Fisher最优分段算法，对其年时序出力进行最优分段；然后利用模糊c均值聚类技术对每一时间段逐一进行聚类分析。使得光伏出力的建模更细化，能较好地保留了其局部特性。以IEEE-RTS测试系统为例，针对宁夏某光伏电站实测出力数据，采用该方法将年评估时间尺度智能划分为5个时间段，并在各时间段上量化分析不同光伏容量对发电系统可靠性的影响。计算结果证明了该方法的有效性，对光伏电站的并网容量规划具有重要指导意义。

光伏电站；Fisher最优分段；模糊c均值聚类；可靠性评估；发电系统

Recently,with the growing PV capacity,analyzing its impacts on reliability ofpower grid accurately has practicalsignif⁃icance.This paper puts forward a novelmethod for modeling the PV output,based on optimalsegmentation and multidimensionalcluster⁃ing method,which can retention circadian and seasonaltiming char⁃acteristics well.Firstly,according to the effective output time of PV in a day,using Fisher optimal segmentation algorithm,year simula⁃tion period gets optimal segmentation.Secondly,using multidimen⁃sionalcluster method offuzzy c⁃mean cluster algorithm,each period is analyzed.This method makes photovoltaic output modeling more refined,and preserves its local properties better.Applied in IEEERTS test system,the reliability analysis uses meas⁃ured PV output in Ningxia.The year simulation period is divided into five optimal periods,and at each period,the impact on power system reliability of PV is analyzed.The resultshows the effectiveness ofthe method, and provides significantguidance on PV capacity planning.

photovoltaic station;Fisheroptimalsegmentation; fuzzy c⁃mean algorithm;reliability assessment;generation systems

10.3969/j.issn.1009-1831.2017.04.005

TM615.2

B光伏历史出力为基础的统计建模［7—10］。直接通过对光伏电站历史输出功率的统计分析，利用蒙特卡罗抽样技术模拟出光伏电站输出功率。该方法大大简化了光电转换模型。其中文献［7］—文献［9］分别使用马尔可夫法、神经网络和基于天气类型的聚类技术，对光伏发电出力进行了统计建模，此类方法相对较繁琐。文献［10］中考虑到光伏出力和负荷具有的日周期特性和相关性，采用一种聚类的技术，分析了光伏发电系统的置信容量，然而采用的可靠性指标只能反映年时间尺度的平均水平，并不能精确刻画一年中各时段光伏对发电系统的影响，其可靠性指标过于粗犷，不能反映光伏出力季节特性。

2017-04-18；

2017-05-28

国家重点研发计划项目课题（2016YFB0900103）；国网江苏省电力公司经济技术研究院科技项目（基于源网荷（储）优化协调的主动配电网示范区规划技术研究）

杨苏（1992），男，江苏盐城人，硕士研究生，研究方向为可再生能源发电，电力系统可靠性评估；黄俊辉（1965），男，湖北黄冈人，本科，高级工程师，研究方向为配电网规划及相关管理工作；关志坚（1971），男，江苏盐城人，硕士，高级工程师，主要从事配电网规划相关管理工作。

随着经济的飞速发展，电力需求不断增加，可再生能源发电得到了广泛关注。其中，光伏发电近年来发展迅速，准确评估含光伏发电的系统可靠性变得十分重要［1—3］。

在对含光伏发电系统的可靠性研究中，光伏出力的建模是当下研究的热点。目前，国内外对光伏出力建模的研究可以分为2类:一类是以太阳能资源为基础的物理建模［4—6］。该类模型中，基于分析辐照强度，温度和光伏阵列角等因素，通过光电转化过程，最终得到光伏系统的输出功率。其建模过程需要的数据量大，而且计算较复杂；另一类是以