智能电网中的家庭用电系统建模与优化分析

杨 明，王元超，向 东，王 丹，付国宏

（华中科技大学 电气与电子工程学院 强电磁工程与新技术国家重点实验室，武汉 430074）

◆研究与探讨◆

智能电网中的家庭用电系统建模与优化分析

杨 明，王元超，向 东，王 丹，付国宏

（华中科技大学 电气与电子工程学院 强电磁工程与新技术国家重点实验室，武汉 430074）

在世界范围内，能源问题日渐凸显，为了应对能源危机，对智能电网的研究在全球范围内得到了广泛的开展［1］，其研究内容覆盖了电能的发、输、配、用的各个环节［2］。智能电网能够促进有序用电和电网经济运行，更合理的分配能源，提高能源利用率，是促进经济社会可持续发展的必然选择［3—4］。随着经济社会的发展，家庭用电量占社会用电总量的比重不断攀升，对家庭用电进行引导，促进其合理有序地用电，具有重要意义。目前，家庭用电系统的智能化正日益受到重视，在节能减排、削峰填谷、提高经济效益等方面，发挥着越来越重要的作用，成为了智能电网中不可或缺的重要组成部分［5—9］。

与工业负荷和商业负荷不同，家庭负荷具有一些独有的特性，而且与居民生活习惯有较大的关联，不能将原有的负荷优化方法直接照搬到家庭负荷的优化中，因此对家庭智能用电系统需要做更深入的研究［10—15］。

文献［10］基于模糊综合评价的方法对居民智能用电行为进行了分析与互动机制的设计。文献［11］从家庭用电规划和家庭能量管理2方面开展了对家庭用电策略的研究，但是没有考虑家庭用电负荷的特性，而仅仅是从时间方面考虑。文献［12］对家庭用电负荷进行了分类，引入了储能装置，但在进行以经济性为目标的优化中，并没有考虑储能等装置的成本，并且仿真步长过大，与家庭负荷的实际情况存在一定的差距。文献［13］利用改进遗传算法对家庭负荷进行了优化，但没有考虑家庭负荷之间的关联性，仅仅将各个用电器作为独立的单元进行优化。文献［14］利用云计算环境下的Apriori关联规则算法对实际生活数据进行挖掘分析，分析了基于用户习惯的负荷时序关系，总结了家庭各个用电负荷之间存在的关联性。文献［15］对家庭用电系统的软硬件实现做了一定的研究。

本文针对家庭用电负荷的连续性、可中断性，以及负荷之间的关联性、顺序性、强依附性等特性，建立了负荷系统、储能系统的模型，将模型转化为利于求解的混合整数线性规划问题，充分考虑了分时电价对家庭用电行为的激励作用，以及相关设备的成本因素，以经济性为目标，进行优化。最后通过算例求解，表明了模型与优化策略的准确性、实用性与有效性。

1 家庭用电系统基础模型

1.1 负荷单元模型

1.1.1 负荷单元工作状态标志

家庭负荷分为基础负荷、连续运行负荷、可中断负荷。负荷之间的关系分为前置负荷关系和强依附性负荷关系。

在一个限定的时间段内，如果一种负荷需要满足一定的运行任务，那么将这个负荷称之为一个负荷单元。这样，对家庭用电负荷的优化就转化为对负荷单元的调度安排。

设Units为家庭用电系统中所有负荷单元的集合，Units={1 ,…,N}包含有N个负荷单元。T为优化周期，T={1 ,…,M} 一个优化周期分为M个时间段。

Li(t)为第i种负荷单元在第t时间段的是否工作的标志，只能取0或1，0表示非工作状态，1表示工作状态。

此外，与工业负荷不同，家庭用电负荷有独有的特点，负荷的启停与居民的作息规律相关，因此家庭负荷的运行都有一定的时间范围，例如电灯一般在晚上时段开启，时间区间表示第i种负荷单元的可运行时间区间，在区间内时，Li(t)可以取0或1，在时间区间外时，只能取0。

1.1.2 负荷单元计划任务

一个限定的时间段内，一种负荷单元需要满足一定的运行任务，用式（2）表示

式中:taski为第i种负荷所需运行的时段的任务数。

1.2 储能装置模型

家庭智能用电系统配备有一定容量的储能电池，用来实现提高供电可靠性、提高经济性等目的。

储能装置的荷电状态(state ofcharge,SOC)是用来描述蓄电池电量的状态变量，用C(t)来表示。C(t)为蓄电池在第t时间段的初始时刻的储存电量。

1.2.1 蓄电池荷电状态SOC

t+1时刻和t时刻的蓄电池电量的迭代关系由式（3）确定，并且为了保证电池寿命，使蓄电池不受损坏，任意时刻的蓄电池电量应当保持在允许的电量范围之内。

式中:σc为储能电池的自放电率，表示电能的自然损耗；Pch(t)、Pdis(t)为储能电池的充放电功率；η1、η2为蓄电池的充、放电效率；Δt为一个时间段的长度；Cmin、Cmax为蓄电池电量的上下限。

1.2.2 蓄电池充放电过程

蓄电池的运行过程，可以归结为充电、放电、不充电不放电3种状态。

式中:pchmax、pdismax为储能电池的最大充、放电功率；ich(t)、idis(t)为储能电池充、放电状态标志。

规定储能电池充、放电状态标志为0—1变量，即只能取0或1，0表示非工作状态，1表示工作状态。

充电功率、放电功率同时大于0的现象，是与实际情况不相符的，因此模型中用式（7）、式（8）和式（9）共同约束了蓄电池不能出现充、放电共存的现象。

此约束下，在任意时间，蓄电池的充、放电状态只可能存在3种可能

1.3 分时电价

虽然当前国内并未大规模实行较为严格的分时电价，但为了促进经济效益的提升，以及随着国民经济水平的进一步提高，在不远的将来分时电价将会逐渐走进每一个家庭。参考现有的关于分时电价的研究［16—18］，将分时电价原理应用于家庭智能用电系统，把全天电价划分为低谷、平段、高峰、尖峰。

2 家庭智能用电系统优化模型

2.1 决策变量

在上一节的模型基础上可以看出，家庭智能用电系统的优化实质上是在调度周期内，对每一个负荷单元i在每一个时间段t内的工作标志Li(t)、以及蓄电池在每一个时间段t内的充、放电功率Pch(t)、Pdis(t)和充放电顺序的调度优化。

2.2 目标函数

在一定的家庭用电模型以及负荷储能电池容量下，优化调度运行方式，使总的经济成本达到最优。

式中:CL为负荷单元运行所需的电费；CE为储能设备建设投资成本；CS为储能设备运行维护费用。

（1）负荷单元运行所需的电费CL

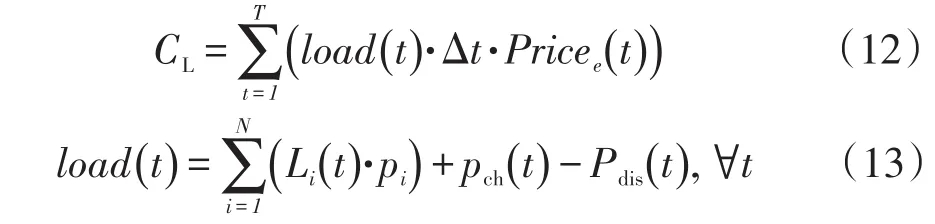
式中:pi表示第i种负荷的功率；load(t)是整个系统的负荷曲线；Pricee(t)为24 h的峰谷电价；Δt是每个时间段的长度。

式（12）表示一个优化周期内运行所需的电费成本。

（2）储能设备建设投资成本CE

式中:cap为装设蓄电池的容量；PriceBAT为储能设备的单价；yea为储能设备的设计使用年限。

式（14）表示储能设备建设投资成本分摊到每一个优化周期内的费用。

（3）储能设备运行维护费用CS

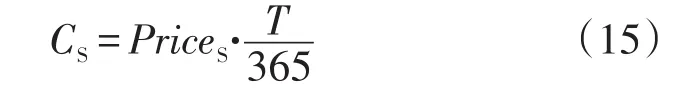
式中:PriceS为储能设备的年运行维护费。

式（15）表示储能设备维护费用分摊到每一个优化周期内的费用。

在式（14）、式（15）中，如果取优化周期为24 h，其结果就是平摊到一天的费用。

2.3 约束条件

2.3.1 前置负荷关系约束

一些负荷之间，存在前置负荷的约束关系，例如:洗衣机和烘干机，要在洗衣机已经完成洗涤任务之后，烘干机开启才有意义。

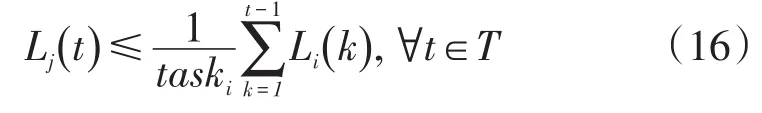
第i种负荷是第 j种负荷的前置负荷，需要按照实际生产安排启停顺序。一个负荷单元启动时，其前置单元必须已经完成所有任务。如果即第i种负荷单元没有完成，则Lj(t)必然等于0；如果，即第i负荷单元已经完成，则Lj()

t可以取0或1。

2.3.2 强依附性负荷关系约束

一些负荷之间，存在更紧密的关联关系，当前置负荷完成之后，后置负荷需要立即开启，例如:洗碗机和消毒柜，洗碗机完成洗涤任务之后，如果放置过久，那将会失去消毒柜的意义，所以，洗碗机完成任务之后，消毒柜应当立即启动。这种关系，成为强依附性负荷关系。

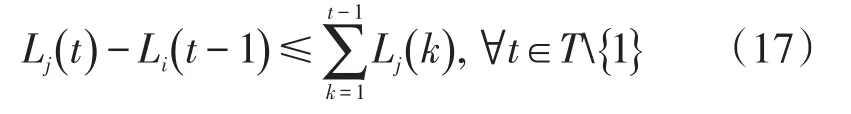
第i种负荷和第 j种负荷之间有强依附性负荷关系，且第i种负荷是第 j种负荷的前置负荷，只有当，Lj()t才能取非零值，与式（16）、式（2）一起保证了在前置负荷单元i完成运行任务时，负荷单元j立即开启运行。

2.3.3 不可中断运行负荷约束

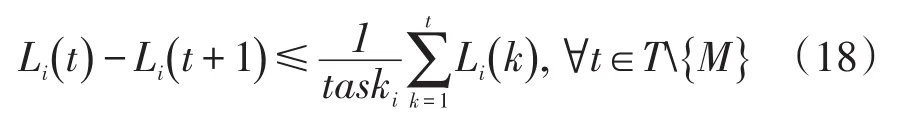
对于不可中断运行的负荷单元，一旦开始运行，必须直到任务完成才能停止，例如:洗衣机等，如果反复的启停，将没有意义。

只有在 Li(t +1)=1，即t+1时继续运行，或者，即任务在t时正好完成的情况下，Li(t)才能取非零值。

2.3.4 最大功率限制约束

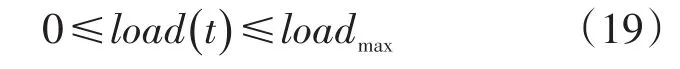
式中:load(t)为t时的总负荷；loadmax为最大功率限制。

为了保证不出现过载现象，任意时刻的负荷不得超过最大负荷限制。

2.3.5 可中断负荷约束

可中断负荷具有较大的优化潜力，比如:空调负荷等，只需满足在规定时间区间内的计划任务约束，即可满足日常用电需求，如式（2）所示。

2.4 模型类型与求解

上述模型构建了家庭智能用电系统的决策变量、目标函数、约束条件。决策变量是0—1整数变量和连续变量，目标函数和约束条件均为线性的。整个问题被归结为混合整数线性规划问题，得到了大大的简化，在求解难度和可操作性上具有优势。

混合整数线性规划问题可以应用数学优化软件包进行求解，如Lingo、Gurobi、Cplex等。本文中采用GurobiOptimization Software。

3 仿真计算与分析

3.1 算例基础数据

选取家庭用电负荷中具有代表性的用电器作为优化对象，如果某一种用电器在不同的时间区间内都有计划任务，将被当作不同的相互独立负荷单元［19—21］。负荷单元基础数据以及负荷间关系数据如表1、表2所示。

其中，电灯和电冰箱是基础负荷，热水器、空调、空气净化器、电动汽车定义为可中断负荷，其他负荷为连续运行负荷。

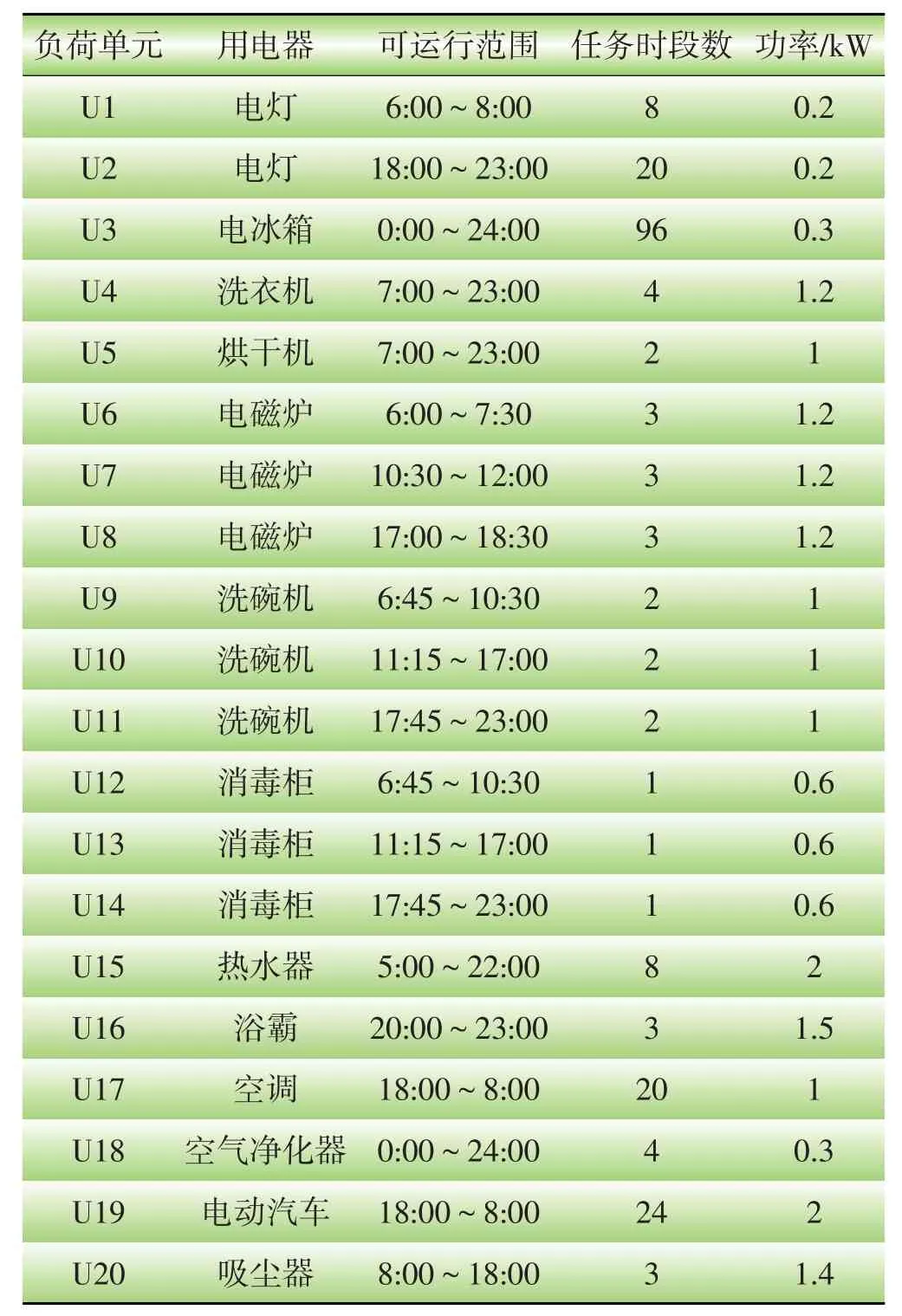
表1 负荷单元基础数据

表2 负荷间关系数据

表2中，“U15—U16”表示U15热水器是U16浴霸的前置负荷；“U11+U14”表示U11是U14的强依附性关系负荷，且U11为U14的前置负荷。其他各组以此类推。

优化调度周期定为24 h，仿真步长为15 min，所以全天均分为96个时段。装设蓄电池容量8 kWh，储能设备成本400元/kWh，年维护费用2.5元/kWh，最大充电功率1.6 kW，最大放电功率3.2 kW，充放电效率95%，系统最大功率限制为10 kW。分时电价具体数据如表3所示。

3.2 优化与结果分析

对模型进行仿真计算，编程环境为数学优化软件MATLAB2014a，由上述算例的目标函数、约束条件来构建混合整数非线性规划方程，通过YALMIP程序接口来调用Gurobi数学规划软件包求解。经过0.98s，Gap值由28.5%降到0%，求得最优解。

表3 分时电价数据

优化后负荷单元运行调度结果如表4所示，家庭24 h负荷曲线如图1所示，蓄电池24 h充、放电优化调度结果如图2所示，蓄电池24 h电量曲线如图3所示。在各负荷单元允许运行时间的范围内随机选取结果，作为优化前的运行数据，优化前电费为24.273 6元，优化后电费为14.772 1元，节省电费9.501 5元，节省了39.14%的电费。

表4 优化调度运行结果

仿真结果中，所有负荷单元都完成了计划任务，且负荷自身约束条件和负荷间关系约束条件都满足。蓄电池电量在电量上下限允许范围内运行，充放电不同时进行，满足蓄电池模型所有约束条件。

从图1优化前后数据对比可以看出，电价较高时段的负荷被显著转移到电价较低的时段，例如: 18：00～21：00尖峰时段中的大部分负荷被转移到了其他时段，而22：00～6：00低谷时段中负荷明显增加，表明在分时电价的指导下，家庭用电行为得到改善，减少在用电高峰时期的用电有利于缓解电网负荷压力，对于家庭来说也节省了电费，提高了经济性。

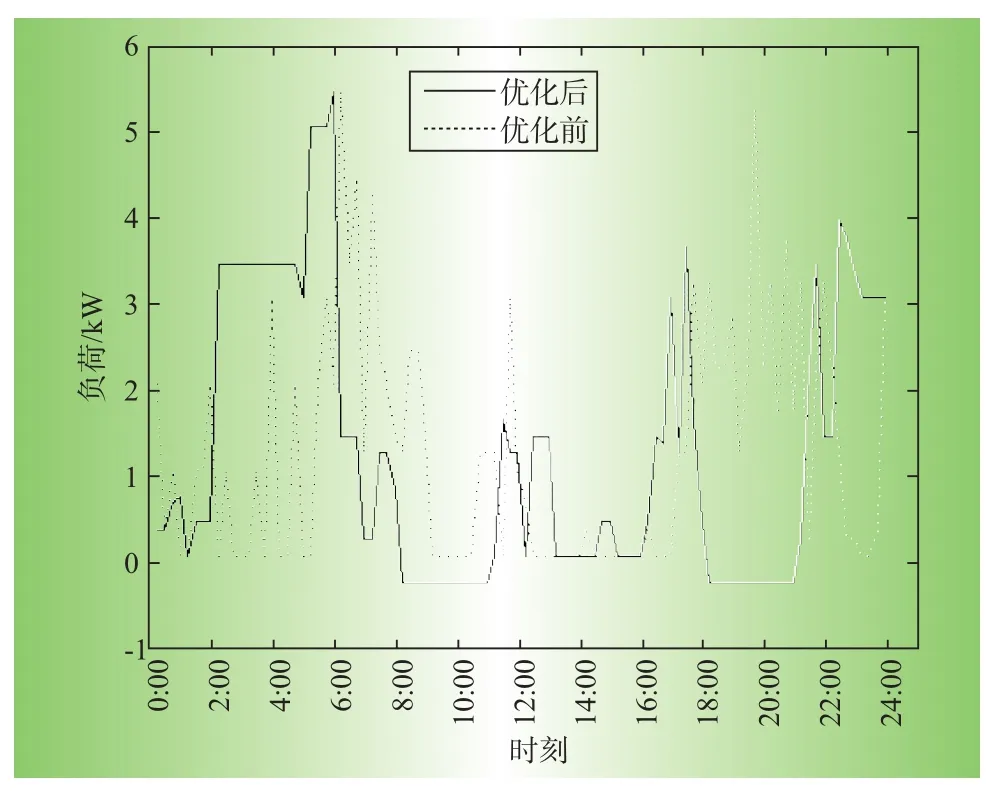
图1 优化前后24 h负荷曲线

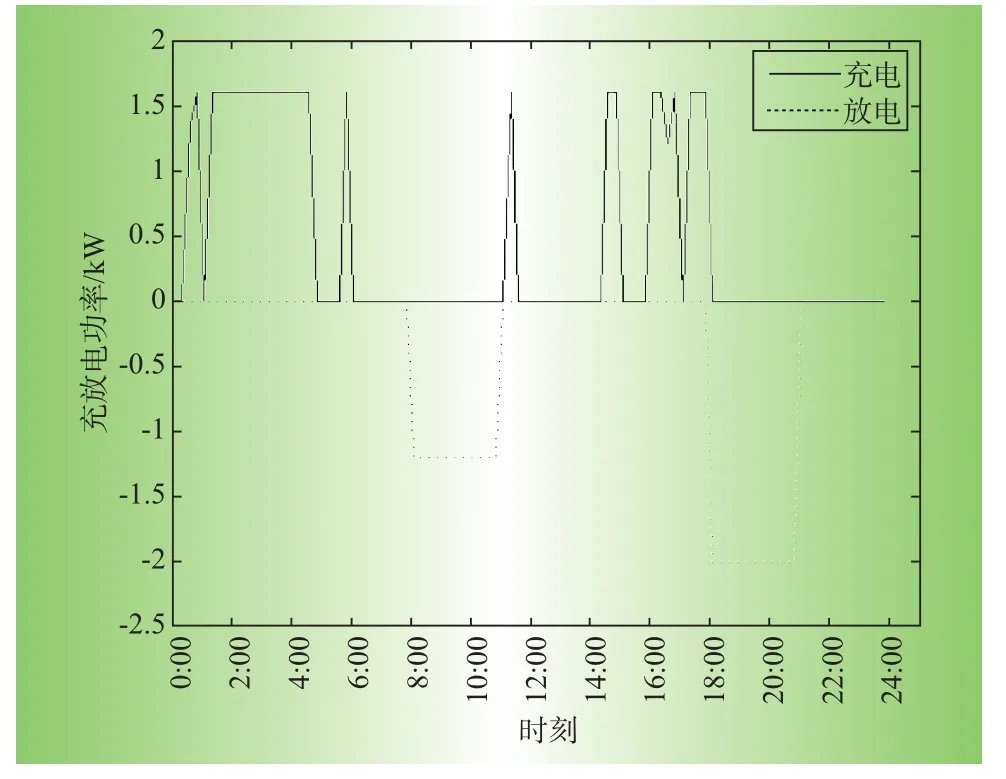
图2 蓄电池24 h充、放电功率曲线

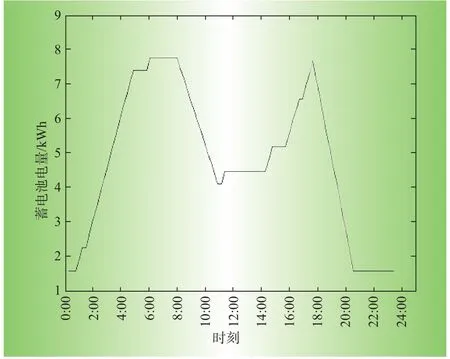
图3 蓄电池24 h电量曲线

4 结束语

本文针对家庭用电负荷，建立了家庭智能用电系统模型，包括负荷模型和蓄电池模型，综合考虑了家庭用电负荷的连续性、可中断性，以及负荷之间的关联性、顺序性、强依附性等特性，将模型转化为利于求解的混合整数线性规划问题；充分考虑了分时电价对家庭用电行为的激励作用，以及相关设备的成本因素，以经济性为目标，得到负荷单元和蓄电池的优化调度运行方式。最后通过仿真算例验证了模型能够准确的描述问题，并使问题得到简化，且优化结果满足各项约束条件，能够实现节省电费、提高经济型的目的，证明了优化策略的实用性与有效性。D

［1］ Fang X,Misra S,Xue G,etal.Smartgrid—the new and improved power grid:a survey［J］.IEEE Communications Surveys&Tutorials,2012,14（4）:944－980．

［2］ 陈树勇，宋书芳，李兰欣，等.智能电网技术综述［J］．电网技术，2009，33（8）:1－7．

［3］ 余贻鑫，栾文鹏.智能电网述评［J］.中国电机工程学报，2009，29（34）:1－8．

［4］ 马其燕，秦立军.智能电网发展状况及其实现建议［J］.电力需求侧管理，2010，12（3）:34－37．

［5］ 刘辉舟，高飞，胡小建，等.分时电价模型优化方法研究［J］.电力需求侧管理，2013，15（4）:11－14，23．

［6］ 辛耀中，石俊杰，周京阳，等.智能电网调度控制系统现状与技术展望［J］.电力系统自动化，2015，39（1）:2－8.

［7］ 陈星莺，陈璐，廖迎晨，等.考虑可中断负荷和需求侧竞价的供电电价模型研究［J］.电力需求侧管理，2010，12（5）:14－18．

［8］ 宋亚奇，周国亮，朱永利.智能电网大数据处理技术现状与挑战［J］.电网技术，2013，37（4）:927－935．

［9］ 田世明，王蓓蓓，张晶．智能电网条件下的需求响应关键技术［J］.中国电机工程学报，2014，34（22）:3 576－3 589．

［10］ 何永秀，王冰，熊威，等.基于模糊综合评价的居民智能用电行为分析与互动机制设计［J］.电网技术，2012，36（10）:247－252．

［11］ 唐二雷.基于智能用电系统的家庭用电策略研究［D］.北京:华北电力大学，2014．

［12］ 王继东，杨羽昊，周越，等．家庭智能用电系统建模及优化策略分析［J］.电力系统及其自动化学报，2014，26（11）:63－66，71．

［13］ 陆青，谢品杰，冷亚军，等.面向家庭智能用电的用电任务调度优化［J］.华东电力，2014，42（5）:816－821．［14］ 郭晓利，于阳.基于云计算的家庭智能用电策略［J］.电力系统自动化，2015，39（17）:114－119，133．

［15］ 王笛.面向家庭的智能用电管理系统的研究与实现［D］.北京:北京交通大学，2015．

［16］ 黄弦超，张粒子，陶文斌.上网侧分时电价设计［J］．电网技术，2013，37（5）:1 317－1 322．

［17］ 程瑜，翟娜娜.基于用户响应的分时电价时段划分［J］.电力系统自动化，2012，36（9）:42－46，53．

［18］ 陈沧杨，胡博，谢开贵，等.计入电力系统可靠性与购电风险的峰谷分时电价模型［J］.电网技术，2014，38（8）:2 141－2 148．

［19］ 汤庆峰，刘念，张建华.计及广义需求侧资源的用户侧自动响应机理与关键问题［J］.电力系统保护与控制，2014，42（24）:138－147．

［20］ 赵波，包侃侃，徐志成，等.考虑需求侧响应的光储并网型微电网优化配置［J］.中国电机工程学报，2015，35（21）:5 465－5 474．

［21］ 王丹，范孟华，贾宏杰.考虑用户舒适约束的家居温控负荷需求响应和能效电厂建模［J］.中国电机工程学报，2014，34（13）:2 071－2 077．

Modeland optimization analysis forhousehold electricity consumption system in smartgrid

YANG Ming，WANG Yuan⁃chao，XIANG Dong，WANG Dan，FU Guo⁃hong
（State Key Laboratory ofAdvanced Electromagnetic Engineering and Technology,SchoolofElectricaland Electronic Engineering,Huazhong University ofScience and Technology,Wuhan 430074,China）

为了实现电网削峰填谷、节约居民用电成本的目的，需要对家庭用电负荷进行更加合理的引导。综合考虑家庭用电负荷的连续性、可中断性以及负荷之间的关联性、顺序性、强依附性等特性，以分时电价为背景，建立了计及储能系统的家庭智能用电系统模型，包括负荷运行模型、蓄电池充放电模型和经济性优化模型。提出利用0—1变量对模型决策变量进行编码，将优化问题转化为混合整数线性规划问题，并采用Gurobi数学规划软件包求解，大大降低了问题的求解难度。在Matlab环境下，对家庭用电负荷数据进行仿真计算，仿真结果表明，模型和优化策略能够实现转移家庭用电负荷以及降低用电费用的目的。

智能电网；家庭智能用电系统；优化；分时电价

In order to realize peak shaving and reduce the cost of household electricity consumption,it is necessary to guide the household electricity load more reasonably.In this paper,accord⁃ing to the continuity and discontinuity of household electricity load and the relevance,order,strong dependence and other characteris⁃tics among household electricity load,in the background oftime⁃of⁃use price,a smart household power consumption system model is built including the load model,the storage battery model and the economic optimization model.A method is presented to transform the optimization problem into a mixed integer linear programming problem by encoding ofthe decision variables modelusing 0-1 vari⁃ables.The problem can be solved by Gurobi programming software, which greatly reduces the difficulty of solving the problem.In the Matlab environment,the simulation of the household electricity load data is carried out.The simulation result shows that the model and the optimization strategy can realize the transfer of household elec⁃tricity load and reduce the costofelectricity.

smartgrid;smarthome power consumption sys⁃tem;optimization;TOU price

10.3969/j.issn.1009-1831.2017.04.002

TM76

B

2017-04-11；

2017-05-29

杨明（1992），男，安徽亳州人，硕士，研究方向为电力系统运行调度与规划；王元超（1989），男，云南宣威人，硕士，研究方向为大型工业企业智能电网；向东（1992），男，湖北巴东人，硕士，研究方向为电力电子在电力系统中的应用等；王丹（1977），男，江西瑞昌人，博士，副教授，研究方向为电力系统运行与控制、大功率电力电子技术在电力系统中的应用；付国宏（1989），男，湖北巴东人，硕士，研究方向为电力电子在电力系统中的应用等。