基于粒子群优化支持向量机的建筑室内温度预测模型＊

庞明月，王文标，汪思源

（大连海事大学信息科学技术学院，辽宁大连116026）

基于粒子群优化支持向量机的建筑室内温度预测模型＊

庞明月，王文标，汪思源

（大连海事大学信息科学技术学院，辽宁大连116026）

建筑系统是一个滞后系统，对下一时刻室内温度的预测可以指导楼宇阀门的开关，从而在保证用户热舒适性的同时节约能源。但是，建筑室内温度受室外气象因素、历史温度等多种非线性因素的影响，机理建模困难。针对以上问题，先确定输入、输出样本，建立支持向量机模型；然后采用粒子群优化（PSO）算法对SVM的核参数和惩罚因子进行动态寻优，建立PSO-SVM预测模型；最后，在MATLAB实验平台上进行仿真实验。实验结果表明，经过粒子群优化的支持向量机预测模型的精度提高至0.6%，可以准确指导楼宇阀门的开关。

室内温度；楼宇阀门；支持向量机；粒子群优化算法

建筑系统是一个复杂系统，它具有非线性、大滞后、多变量、耦合严重、变化缓慢等特点。利用建筑系统大滞后的特点可以预测下一时刻的室内温度，从而指导楼宇阀门的开关，在保证用户热舒适性的同时节约能源。但是，在供暖期，建筑室内温度受室外气象因素、历史温度等多种非线性因素的影响，使建筑室内温度机理建模变得复杂且困难[1]。支持向量机（SVM）为解决上述问题提供了一个可行的方案。支持向量机是小样本学习领域的重要应用理论和算法，它具有结构简单、推广能力强等特点。因此，本文选取支持向量机方法为建筑室内温度建模，并利用粒子群算法优化参数，以提高模型的精度。经过实验，结果验证SVM非常适用于建筑室内温度的非线性预测。

1 基于SVM模型

1.1 支持向量机的基本原理

SVM方法的基本思想是，基于Mercer核展开定理，通过非线性变换将样本空间映射到一个高维空间中，在高维空间中寻找最优线性回归超平面。简单地说，就是升维和线性化[2]。通过构造损失函数，并基于结构风险最小化思想，支持向量机通常采用极小化优化模型确定回归函数[3-5]，即：

引入Lagrange乘子，式（1）、式（2）所示的优化模型可转化为以下对偶优化问题予以求解[6]，即：

求解上述问题可得到支持向量机回归函数，即：

式（5）中：K（x，xi）为核函数，需满足Mercer条件。

要构造出一个具有良好性能的SVM，核函数的选择是最关键也是最重要的一步。根据专家经验，本文选择径向基（RBF）函数[7-9]作为核函数建立SVM预测模型，径向基函数形为：

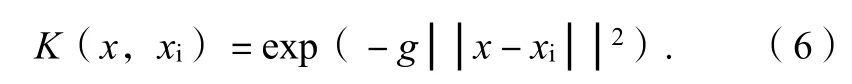
式（6）中：x为待预报因子向量；xi为作为支持向量的样本因子向量；g为核函数参数。由此可见，支持向量机计算过程中涉及到2个参数，即权重系数C和核函数参数g。

1.2 数据归一化处理

本文中的测量数据有不同的量纲，数值的大小差别很大，数据分布范围也不一样，数据平均值和方差有较大的差异，这样会夸大某些变量对目标的作用，掩盖某些变量对目标的贡献，不能准确地为建筑室内温度建模。因此，必须先对数据进行归一化处理，建模之后再对预测结果进行反归一化处理。本文中选用MATLAB自带的mapminmax函数先将数据归一化到[-1，1]，其调用格式为：

再将预测结果进行反归一化，其调用格式为：

式（7）（8）（9）中：X为原始数据；Y为进行归一化后得到的数据；PS中存放归一化的映射记录。

2 PSO参数寻优

由于建立精确的SVM模型需要确立惩罚因子C和RBF的核参数g，惩罚因子C过大或者过小都会影响模型的泛化能力或训练误差，核参数g过大或者过小可能会引发过拟合或者欠学习现象[10]，所以，合理选取优化算法对SVM最佳参数的确立至关重要。本文选用PSO进行参数寻优。该算法首先初始化一群随机粒子，然后通过迭代，粒子通过跟踪2个“极值”更新自己的位置，从而找到最优解[11]。采用PSO优化算法对惩罚因子C和核参数g进行寻优，具体步骤如下：①确定适应度函数；②初始化种群和速度；③计算适应度函数；④适应度定标；⑤速度更新、个数更新；⑥当不满足终止条件时，返回步骤③，满足终止条件，继续执行；⑦确定最优解；⑧输出最优解。

在本文参数动态寻优过程中，设置学习因子c1＝1.5，c2＝1.7，种群最大数量s＝20，k＝0.6，wV＝1，wP＝1，v＝5，最大进化数量m＝200，cmax＝100，cmin＝0.1，gmax＝1 000，gmin＝0.01.经过参数寻优后，cbest＝24.49，gbest＝0.01.

3 实验及结果分析

3.1 仿真实验

以大连某高校一栋办公楼为例，选取2016-01-27—02-01这段时间，每隔0.5 h收集一次数据，共收集288组数据进行实验。前240组数据作为训练样本，后48组数据作为测试样本，选取时间、日照、室外温度、供水温度、当前室温作为模型输入，选取下一刻室内温度作为模型输出。

对于支持向量机模型，先用前240组数据作为训练样本进行训练，训练结束后获得支持向量机模型，再用后48组数据测试。图1为SVM预测值与实际值曲线图。

在支持向量机模型的基础上用粒子群算法对模型参数进行寻优，同样用前240组数据进行训练，后48组数据进行测试。图2为PSO-SVM预测值与实际值曲线图。

3.2 实验结果分析

为了对比SVM与PSO-SVM的预测效果，将平均绝对误差eMAE、均方误差eMSE和均方根误差eRMSE作为判断依据。SVM和PSO-SVM的预测误差值如表1所示。

图1 SVM预测值与实际值曲线图

图2 PSO-SVM预测值与实际值曲线图

表1 SVM和PSO-SVM的预测误差值

从表1中可以看出，PSO-SVM的eMAE、eMSE、eRMSE均小于SVM。这说明，经过粒子群优化SVM模型的预测精度更高，可以应用于建筑室内温度的非线性预测方面。

4 结论及展望

针对建筑室内温度预测问题，本文提出了一种基于粒子群优化支持向量机的建筑室内温度预测模型，选取大连市某高校一栋典型的办公类建筑，将室外气象参数等作为输入，将建筑室内下一时刻室内温度作为输出，建立了SVM预测模型，应用PSO优化SVM的参数。结果表明，经过粒子群优化的SVM模型的预测值更加接近真实值，精度高至0.6%，能够准确指导楼宇阀门的开关。

［1］李康吉.建筑室内环境建模、控制与优化及能耗预测［D］.杭州：浙江大学，2013.

［2］王革丽，杨培才，毛宇清.基于支持向量机方法对非平稳时间序列的预测［J］.物理学报，2008，57（02）：714-719.

［3］李海生.支持向量机回归算法与应用研究［D］.广州：华南理工大学，2005.

［4］李霄，王昕，郑益慧，等.基于改进最小二乘支持向量机和预测误差校正的短期风电负荷预测［J］.电力系统保护与控制，2015，43（11）：63-69.

［5］王贺，胡志坚，张翌晖，等.基于聚类经验模态分解和最小二乘支持向量机的短期风速组合预测［J］.电工技术学报，2014，29（4）：237-245.

［6］王宁，谢敏，邓佳梁，等.基于支持向量机回归组合模型的中长期降温负荷预测［J］.电力系统保护与控制，2016，44（03）：92-97.

［7］陈伟根，滕黎，刘军，等.基于遗传优化支持向量机的变压器绕组热点温度预测模型［J］.电工技术学报，2014，29（1）：44-51.

［8］LIU Xianglou，JIA Dongxu，LI Hui，et al.Research on kernel parameter optimization of support vector machine in speaker recognition［J］.Science Technology and Engineer，2010，10（7）：1669-1673.

［9］王东，史晓霞，尹交英.不同核函数的支持向量机用于空调负荷预测的对比研究［J］.电工技术学报，2015，30（S1）：531-535.

［10］王文剑，门昌骞.支持向量机建模及应用［M］.北京：科学出版社，2014：211.

［11］赵志刚，张纯杰，苟向锋，等.基于粒子群优化支持向量机的太阳电池温度预测［J］.物理学报，2015，64（8）.

〔编辑：白洁〕

TP18；TU832

A

10.15913/j.cnki.kjycx.2017.18.014

2095－6835（2017）18－0014－04

大连市科技计划项目（2014E11SF059）、中央高校基本科研业务费专项资金资助