基于采样压缩的加速K-NN分类方法
2017-09-16王晓
王晓
(晋中学院信息技术与工程学院,山西晋中030619)
基于采样压缩的加速K-NN分类方法
王晓
(晋中学院信息技术与工程学院,山西晋中030619)
标准K-近邻分类方法(K-Nearest Neighbor,K-NN)在进行样本预测过程时,需要计算每一个待预测类别标记的样本与所有已知标记样本的距离,因此复杂度较高,无法处理含有大规模有标记样本的分类问题。针对这个问题,本文提出一种基于采样压缩的加速K-NN分类方法(K-NN Method Based on Sampling Compress, KNN_S)。该方法将采样思想引入到K-NN分类过程当中,即对于每一个新来的未知类别的待测样本,不是计算其与所有带类别标签样本的距离,而是通过采集一定数量的有标记样本,计算这部分有标记样本中距离待测样本最近的近邻样本,来对待测样本进行分类。实验结果表明,本文提出的KNN_S方法能够加速K-NN分类的过程。
K-NN分类;采样;KNN_S算法;距离
K近邻(K nearest neighbor,K-NN)分类方法[1-2]是一种最为常见的分类预测方法,其模型设计简单,容易实现,且分类的可靠性往往较高,目前已经在多种领域中得到了成功应用[3-5]。然而,随着现实应用问题中数据量的不断增长,分类方法需要处理的数据规模越来越大,对于K-NN分类模型,当有类别标记的样本规模非常大时,由于其在对新样本类别的预测过程中需要计算新样本到所有已标记样本的距离,因此计算距离的耗时较多,无法有效处理大规模数据的分类问题[6-9]。
针对这个问题,本文提出一种基于采样压缩的加速K-NN分类方法。该方法将随机采样思想引入到K-NN分类过程当中,即对于一个待测样本,不是计算其与所有样本的距离,而是通过采集一定数量的有标记样本来压缩实际参与决策的带标记样本集,计算这部分带标记样本中距离待测样本最近的k个近邻样本,然后对待测样本按照少数服从多数的原则进行分类。由于计算距离的数目较少,因此分类的效率会相应提高。
1 标准K-近邻分类方法
假设存在带类别标记的样本x1,x2,…,xn,且已知这些样本对应的的类别标签分别为y1,y2,…,yn,其中xi为p维空间中的样本,其类别标签yi∈{+1, -1},待测试样本为t1,t2,…,tm,近邻参数为k。KNN方法对于任意一个待测试样本tj,都需要计算该样本与所有带标记样本xi的距离,p维空间中的距离计算如下:

根据上述距离公式,即可比较得到距离待测试样本tj最近的k个带标记样本,然后根据该k个带标记的近邻样本的类别标签对待测样本根据少数服从多数的原则进行打标签。
在K-NN分类方法中,假设有标记样本的规模为n,样本维度为 p,则对于每一个待测样本来说,预测其类别标签的其复杂度可以写成O(np),整个算法执行的复杂度即为O(npm),其中m为待测试样本个数,然而在实际问题中,有标签样本集的规模往往较大(若该样本集过小又缺乏代表性时,分类结果精度不高),此时算法的时间复杂度较高,无法在大规模数据集上执行。
2 基于采样的加速K-NN算法
针对传统K-NN分类方法无法处理大规模带标签数据的分类学习问题,本文提出了一种基于采样压缩的加速K-NN分类方法,该方法首先对带标签的样本进行随机抽样,即得到一个抽样集合{x1',x2',…,xn''},假设抽样的规模为n'且n'<<n,即抽样样本的规模要远小于原始带标签样本的规模,当一个待测样本t进入时,首先计算待测样本t与抽样样本集{x1',x2',∙∙∙,xn''}中每一个抽样样本的距离,压缩实际参与类别决策过程的带标签样本数,并根据距离选择最近的k个抽样样本集中的样本,然后根据少数服从多数的原则对待测样本来标记类别标签。
KNN_S分类算法的具体执行过程如下。
初始化:假设带类别标签的训练样本集为x1,x2,∙∙∙,xn,其对应的类别标签为 y1,y2,∙∙∙,yn,其中 xi为p维空间中的样本,其类别标签yi∈{+1,-1},测试样本为t1,t2,∙∙∙,tm,测试样本对应的真实类别标签为y1,y2,∙∙∙,ym,近邻分类参数设置为k,抽样参数设置为s,s∈(0,1]。
Step1:对带有类别标签的样本集x1,x2,∙∙∙,xn进行随机抽样,假设得到的抽样样本集结果为{x1',x2',∙∙∙xn''},对应的类别标签为{y1',y2',∙∙∙,yn''},既有如下的抽样本规模关系:

Step2:计算每个待测样本tj到压缩后的带标签抽样样本xi'的距离,计算方法类似于式(1),即:

Step3:选择距离最近的k个压缩后的样本集中的带标签样本,并根据这k个近邻的标签以少数服从多数的原则对待测试样本tj进行打预测类别标签;
Step4:对于每一个待测样本,都循环执行Step2-Step3的过程,直到所有待测样本的预测类别标签y1',y2',∙∙∙,ym'都得到时为止;
Step5:根据待测样本得到的预测类别标签y1',y2',∙∙∙,ym'与其真实的类别标签 y1,y2,∙∙∙,ym进行对比,得到分类器性能的好坏;
Step 6:算法结束。
假设KNN_S分类方法中,有标记样本的规模为n,抽样压缩之后的样本规模为n',则对于每一个待测样本来说,其预测标签过程的复杂度变为O(n'p),当然,抽样压缩之后的带标签样本集只是原始样本集的一个尽可能优秀的表示,但根据其得到的分类结果肯定无法与原始分类结果一致,而只能是一种近似的逼近。在实际问题中,可以根据用户的任务需求来设置抽样参数s,若用户任务对分类精度要求较高,则应该设置较大的抽样参数值,即有较小的抽样压缩比例,当然此时效率的提升不明显,当用户任务对分类效率的要求较高时,可以设置较小的抽样参数值,以有效压缩实际参与类别决策的有标记样本的数量,提高预测过程的学习效率。
3 实验结果及分析
为验证本文所提出的ISVM_S学习方法的性能,本文在构造的正态分布数据集和3个典型的UCI数据集上进行了测试。人工构造的正态分布数据集中,正类和负类分别以(+1,+1)和(-1,-1)为中心,以(1 0,0 1)为协方差矩阵来构造,其中正类和负类的比例分别为500:500。测试集与训练集构造方法一致,人工构造的训练集分布如图1所示。
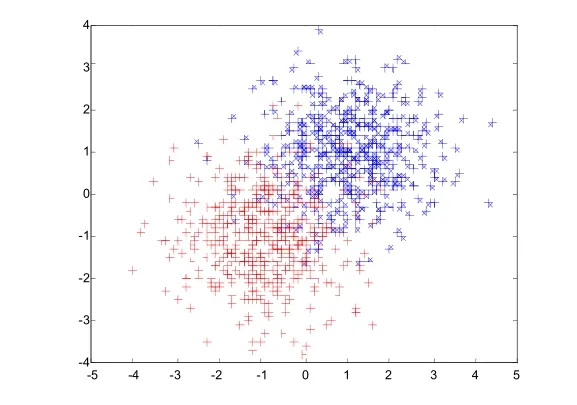
图1 人工构造的正态分布数据集
实验中采用的标准UCI分类数据集如表1所示。

表1 实验数据集
由于影响KNN_S算法性能的参数主要为样本压缩参数s,因此本文测试了在不同的样本压缩参数s下的实验结果。本文将实验结果与标准的K-NN进行了比较,实验中近邻参数取5,人工数据集的实验结果见表2。表中第一行数值为样本压缩参数,由于人工构造的正态分布数据集规模较小,因此抽样压缩参数分别取10%、20%、30%、40%和50%。

表2 人造数据集上的测试精度
从实验结果可以看出,对于不同压缩比的人造正态分布数据集,本文提出的KNN_S方法与传统K-NN相比,在多数压缩比参数下,其方法的精度都与K-NN接近(特别地,当参数取30%、40%和50%时),测试精度与K-NN均相同,这是由于人造的正态分布数据集本身样本分布简单,容易区分两类样本,当然,压缩比降低到10%之后,精度与KNN相比,还是存在4%的差距。但从算法的运行效率上看,在5个不同的抽样压缩参数下,算法的效率都有了明显的提高,提高值达到了100%到800%,特别指出的是,当样本压缩参数取30%时,算法所需要的类别预测时间仅为原来的36%,但测试精度与标准K-NN一致。
在真实的UCI数据集上的实验结果如表3所示。由于UCI数据集规模较大,因此抽样压缩参数分别取5%、10%、15%、20%和25%。

表3 UCI数据集上的实验结果
从表3在标准的UCI数据集上进行测试的结果可以看出,在Banana数据集上,在所有抽样压缩参数下得到的分类精度均与K-NN一致,而分类时间却提高了100~120s左右;同理,在Diabetis数据集上,KNN_S方法也得到了与K-NN基本一致的分类结果,且在预测效率方面有明显的提高。这说明虽然二者均为真实的数据集,数据分布可能较为复杂,但由于带标签数据的规模较大,因此抽样压缩基本上不会影响类别预测的结果。但在数据集German上,与标准K-NN分类方法相比,虽然在预测效率上有了明显提高,但预测精度却存在明显下降,特别地,当抽样压缩参数取5%时,测试精度降低了11.8%,这可能是由于该数据集为高维数据集,因此抽样结果对于距离分布敏感,因此抽样压缩得到的带标记样本与原始整体带标记样本分布存在较大差异,导致分类预测结果不好。
4 结语
基于采样压缩的加速K-NN分类方法,将采样思想引入到K-NN分类过程当中,对每个待测样本,通过采集一定数量的有标记样本,计算这部分有标记样本中距离待测样本最近的近邻样本,减少了计算距离的个数,提高了分类的效率。
[1]LIU Z G,PAN Q,Dezert J.A new belief-based K-nearest neighbor classification method[J].Pattern Recognition,2013,48(3):834-844.
[2]MITCHELL H B,SCHAEFER P A.A“soft”K-nearest neighbor voting scheme[J].International Journal of Intelligent Systems,2001 (16):459-468.
[3]彭凯,汪伟,杨煜普.基于余弦距离度量学习的伪K近邻文本分类算法[J].计算机工程与设计,2013,34(6):2200-2203,2211.
[4]杨帆,林琛,周绮凤,等.基于随机森林的潜在k近邻算法及其在基因表达数据分类中的应用[J].系统工程理论与实践,2012,32(4):815-825.
[5]郭玉堂.基于互K近邻图的自动图像标注与快速求解算法[J].计算机科学,2011,38(2):277-280.
[6]LIU Z G,PAN Q,DEZERT J.A new belief-based K-nearest neighbor classification method[J].Pattern Recognition,2013,48(3): 834-844.
[7]刘应东,牛惠民.基于K-均值聚类的小样本集KNN分类算法[J].计算机应用与软件,2011,28(5):112-113.
[8]NICOLAS G P,DOMINGO O B.Boosting k-nearest neighbor classifier by means of input space projection[J].Expert Systems with Applications,2009,36(7):10570-10582.
[9]HART P E.The condensed nearest neighbor rule[J].IEEE Transactions on Information Theory,1968,14(3):515-516.
Speeding K-NN Classification Method Based on Sampling Compress
WANG Xiao
(School of Information Technology&Engineering,Jinzhong University,Jinzhong Shanxi,030619)
This paper presents a K-Nearest Neighbor(KNN)method based on sampling compress,called KNN_S,in order to solve the problem that the low training efficiency and cannot solving the large scale problems of normal K-NN because it need compute the distance between the sample to be tested and the labeled samples in the new sample classification prediction process.By introducing the sampling idea into the K-NN classification process,when the new sample to be tested is produced,this method is not computing all the distances between all the labeled samples and the new sample,but it executed by computing the distances between the new coming sample and the compressed samples by sampling process to classify the prediction sample.The experiment results demonstrate that the proposed KNN_S method can speed the K-NN classification process.
K-NN classification;sampling;KNN_S algorithm;distance
TP18
A
〔责任编辑 高海〕
1674-0874(2017)04-0017-04
2016-11-15
王晓(1980-),男,山西汾阳人,硕士,讲师,研究方向:人工智能与数据挖掘。
