配电网大数据蒙特卡洛矩阵模拟评价体系

傅晓飞，廖天明，纪坤华

(国网上海市电力公司运维检修部，上海 200122)

配电网大数据蒙特卡洛矩阵模拟评价体系

傅晓飞，廖天明，纪坤华

(国网上海市电力公司运维检修部，上海 200122)

构建一种基于配电网大数据分析的模糊综合评价体系，采用蒙特卡洛方法形成蒙特卡洛矩阵,并进行模拟评价。依据模糊综合评价体系,对配电网现状进行诊断,对规划实施效果进行理论检验,为配电网的建设改造提供有力的依据。以上海某供电公司供电线路实际运行数据为例进行分析，对两条供电配电网进行综合评价。

模糊综合评价；蒙特卡洛；配电网大数据；数据关联

配电网直接面向终端用户，在可靠供电、促进地区经济发展、保持社会和谐稳定等方面发挥着举足轻重的作用。经过多年的建设与改造，我国配电网的结构和供电能力得到了不断改善。为提高配电网规划建设的科学性、指导性和可操作性，开展了配电网评价体系的研究工作。

配电网具有结构复杂、设备数量庞大、改造建设频繁等特点[1]，对其进行综合评价所涉及的因素众多。目前，对配电网进行评价的做法通常是从供电可靠性、经济性、安全性、供电质量等单一特性指标出发[2-6]，从不同侧面评价配电网的技术水平。文献[7]从技术合理性、安全性等多个角度出发，针对现状配电网建立了较为全面的评价指标体系，并通过实例给出评估方法。文献[8]提出了基于区间层次分析法的城市电网规划综合评判决策方法。文献[9]运用层次分析法和德尔菲法对现状电网的综合指标进行评价。这些研究成果侧重于传统技术指标，主要反映配电网的运行水平和供电能力，缺乏整体性评价，对电网建设的直接指导性还不够强。

本文构建一种基于配电网大数据分析的模糊综合评价体系，并采用蒙特卡洛方法形成蒙特卡洛矩阵，进行模拟评价。依据模糊综合评价体系，对配电网现状进行诊断，对规划实施效果进行理论检验，为配电网的建设改造提供有力的依据。

1 综合评价理论基础

1.1层次分析法

层次分析法的核心思想是通过建立清晰的层次结构来分解复杂问题[10]，它能够在有效处理各评价指标之间的内在联系及相互独立性的基础上，量化并综合各个指标，具有较强的灵活性和整体性，是评估中分析复杂问题和建立评估体系的关键技术。

层次分析法的基本步骤可归纳如下。

(1)针对评价目标建立清晰的层次结构，形成评价指标体系。

(2)通过两两比较的相对标度法逐层建立判断矩阵，将人的主观判断标量化。

(3)判断矩阵一致性校验通过后，求解各层判断矩阵的属性权重。

(4)计算评价对象的综合评价值并排序。

1.2鱼骨图分析法

鱼骨图分析法将问题的特性与受影响的因素按相互关联性整理成层次分明、条理清楚，并标出重要因素的图形[11]，是一种透过现象看本质的分析方法。可将某一问题或现象细分为若干方面来寻找原因，列举出要改善某一现状或达到某一目标可能需要的若干对策。

1.3模糊综合评价法

模糊综合评价法是一种以模糊集合论为基础，对分析评价中的各种模糊信息作量化处理并进行状态判断的分析方法[12]。它采用隶属程度来描述差异的中间程度，能够将定性指标进行合理的量化，使综合评价中原始数据的不确定性及评价标准的模糊性等问题得到了较好地解决。在确定指标的评价标准时，根据指标类型，将隶属度评价函数分为效益型(正指标)、成本型(负指标)和适中型(中间型指标)三类。本文采用模糊综合评价法对配电网运行进行指标评价。

2 配电网运维指标

2.1供电可靠性指标

供电可靠性是指供电系统持续供电的能力，是考核配电网供电质量的重要指标，主要包括供电可靠率、用户平均停电时间、用户平均停电次数、系统停电等效小时数等指标，反映了电力工业对国民经济电能需求的满足程度，已经成为衡量一个国家经济发达程度的标准之一。上海电网供电可靠率已达到99.999%以上，但是与国际先进城市电网，如东京、巴黎、新加坡等供电可靠率达到99.9999%的地区相比，仍存在较大的差距。

在实际配电网运维与指标评价中，城市用户供电可靠率=(1-用户平均停电时间/统计期间时间)×100%

其中：

(1)范围是指市中心+市区+城镇；

(2)用户平均停电时间=自动采集用户平均停电时间/数据规范率

其中： 数据规范率=(停电数据自动抽查完整率+自动采集事件转换成功率+停电事件采集完整率+线路分段准确率+用户平均停电时间完成偏差率+可靠性水平聚类结果偏差率)/6，其中数据规范率>80%，取值 1。

停电数据自动抽查完整率=(1-漏报停电用户/抽查停电事件中的总停电用户)×100%，按照指定的时间范围， 抽取一定数量的 95598 停电记录等原始停电记录，核查系统漏报数量及其占抽取事件总数的比率；

自动采集事件转换成功率=(1-终端停电事件转换失败数量/(可靠性用户停电数据接入量+终端停电事件转换失败数量))；

停电事件采集完整率=集成停电户次数/集成停电线段下属用户总数(4)线路分段准确率=核查准确线段数/核查线段总数；

用户平均停电时间完成偏差率=用户平均停电时间/用户平均停电时间基准值，注：基准值根据年度目标及历史 3 年平均值进行核定；

可靠性水平聚类结果偏差率=(1-(某单位用户平均停电时间统计值-同类单位用户平均停电时间中位数)/同类单位用户平均停电时间中位数)。

2.2线损率

线损率是指电力网络中损耗的电能(线路损失负荷)占向电力网络供应电能(供电负荷)的百分数，线损率是考核电力系统运行经济性的最直接指标。线损是反应电网规划设计、技术装备和经济运行水平的综合性技术经济指标，线损率的降低将直接为电网公司产生利润。

在实际配电网运维中，线损率的规定为：分区月线损率在0～8%为合格；35 kV及以上分区月线损率在0～3%为合格；10 kV月线损率在0～5%合格；35 kV及以上线路分线线损率0～3%为合格；10 kV分线线损率0～10%为合格，台区线损率0～10%为合格。

2.3电压合格率

电压合格率是实际运行电压在允许电压偏差范围内累计运行时间和对应的总运行时间的百分比。国家电网公司主要考核A、B、C、D四类电压监测点：

A类——带地区供电负荷的变电站和发电厂的20 kV，10(6) kV各段母线电压；

B类——35 kV，20 kV专线和110 kV及以上用户端供电电压；

C类——35 kV和20 kV非专线以及10(6) kV用户端供电电压；

D类——380/220 V低压网络和用户端供电电压。

在实际配电网运维与指标评价中，综合供电电压合格率为：

综合供电电压合格率=0.5×A类监测点合格率+0.5×(B类监测点合格率+C类监测点合格率+D类监测点合格率)/3

其中：监测点电压合格率=(1-(电压超上限时间+电压超下限时间)/电压监测总时间)×100%。

电压合格率是供电压质量的主要考量指标，电压合格率提高也意味着电压质量的提高。

2.4电能质量

电能质量即电力系统中电能的质量，反映了供电企业向用户供给的电力是否合格，从严格意思上讲，衡量电能质量的主要指标有电压、频率和波形。从普遍意义上讲是指优质供电，包括电压质量、电流质量、供电质量和用电质量。

3 配电网模糊综合评价方法

配电网模糊综合评价方法依据该指标体系由低到高逐层进行评价，把诸因素对待评对象的影响通过不同层次和不同阶段较为直观地表现出来。具体评价步骤及公式如下。

(1)假设配电网评价指标中包含{A1，A2，…Ai…}等若干个指标，如Ai代表电压合格率、设备故障率、供电可靠率等。

(2)配电网运行参数包含{B1，B2，…Bk…}等若干个参数，如Bk代表馈线电流、天气温度、电压等。

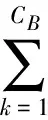
(4)根据配用电实际运维情况收集基础数据，对于因素层中各运行参数{B1，B2，…Bk…}计算其评价得分{E1，E2，…Ek…}。

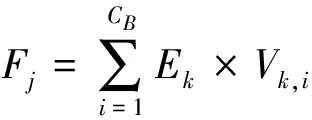
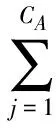
4 配电网大数据蒙特卡洛矩阵模拟评价体系

4.1配电网综合评价指标矩阵

根据介绍的模糊综合评价方法，可得到配电网综合评价的得分G计算得到：

G=E×V×W

(1)

其中：

E=[E1，E2，…Ek…ECB]

(2)

是配用电运行参数的{B1，B2，…Bk…}评价得分矩阵。

(3)

是配用电运行参数{B1，B2，…Bk…}与配电网评价指标中包含{A1，A2，…Ai…}的关联置信度归一化系数矩阵。

(4)

是配电网评价指标中包含{A1，A2，…Ai…}在总评价指标中所占权重系数矩阵。

这些影响配电网综合评价的得分G的三大参数中，W由管理人员根据实际情况确定，V中Vk，j可由基于Apriori关联算法的配电网运行大数据关联分析模型确定，E中配用电运行参数的评价得分矩阵，由于运行参数具有变化和不确定特性，故可以采用模拟方法确定E矩阵中各参数评价得分。

本文采用蒙特卡洛模拟方法，构建配用电运行参数的蒙特卡洛评价矩阵，抽样仿真后计算得到期望配电网综合评价得分，用于评价配电网运行情况。

4.2蒙特卡洛(Monte Carlo)模拟法

蒙特卡洛(Monte Carlo)模拟是一种通过设定随机过程，反复生成时间序列，计算参数估计量和统计量，进而研究其分布特征的方法。具体的，当系统中各个单元的可靠性特征量已知，但系统的可靠性过于复杂，难以建立可靠性预计的精确数学模型或模型太复杂而不便应用时，可用随机模拟法近似计算出系统可靠性的预计值；随着模拟次数的增多，其预计精度也逐渐增高。由于涉及到时间序列的反复生成，蒙特卡洛模拟法是以高容量和高速度的计算机为前提条件的，因此只是在近些年才得到广泛推广。

蒙特卡洛模拟方法的原理是当问题或对象本身具有概率特征时，可以用计算机模拟的方法产生抽样结果，根据抽样计算统计量或者参数的值；随着模拟次数的增多，可以通过对各次统计量或参数的估计值求平均的方法得到稳定结论。

蒙特卡洛模拟法求解步骤：应用此方法求解工程技术问题可以分为两类:确定性问题和随机性问题。

解题步骤具体如下。

(1)根据提出的问题构造一个简单、适用的概率模型或随机模型，使问题的解对应于该模型中随机变量的某些特征(如概率、均值和方差等)，所构造的模型在主要特征参量方面要与实际问题或系统相一致。

(2)根据模型中各个随机变量的分布，在计算机上产生随机数，实现一次模拟过程所需的足够数量的随机数。通常先产生均匀分布的随机数，然后生成服从某一分布的随机数，方可进行随机模拟试验。

(3)根据概率模型的特点和随机变量的分布特性，设计和选取合适的抽样方法，并对每个随机变量进行抽样(包括直接抽样、分层抽样、相关抽样、重要抽样等)。

(4)按照所建立的模型进行仿真试验、计算，求出问题的随机解。

(5)统计分析模拟试验结果，给出问题的概率解以及解的精度估计。

4.3配电网大数据蒙特卡洛矩阵模拟评价体系

根据配电网模糊综合评价方法，配电网综合评价得分G：

G=E×V×W

(5)

其中：V是通过配电网运维大数据Apriori关联分析方法得到；W中的权重系数由人工设定；E可由蒙特卡洛模拟法进行模拟仿真得到。

采用蒙特卡洛模拟法，针对配用电运行参数的评价得分矩阵进行抽样，可形成蒙特卡洛模拟矩阵E：

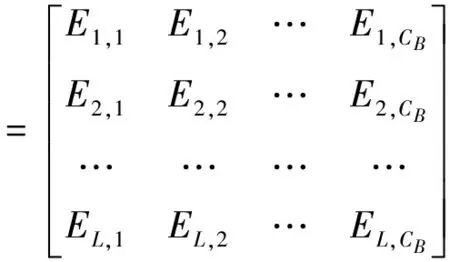
(6)

其中L为抽样次数。

根据G=E×V×W可得到G：

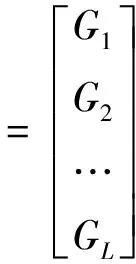
(7)

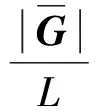
配电网大数据蒙特卡洛矩阵模拟评价体系实现流程图如图1所示。

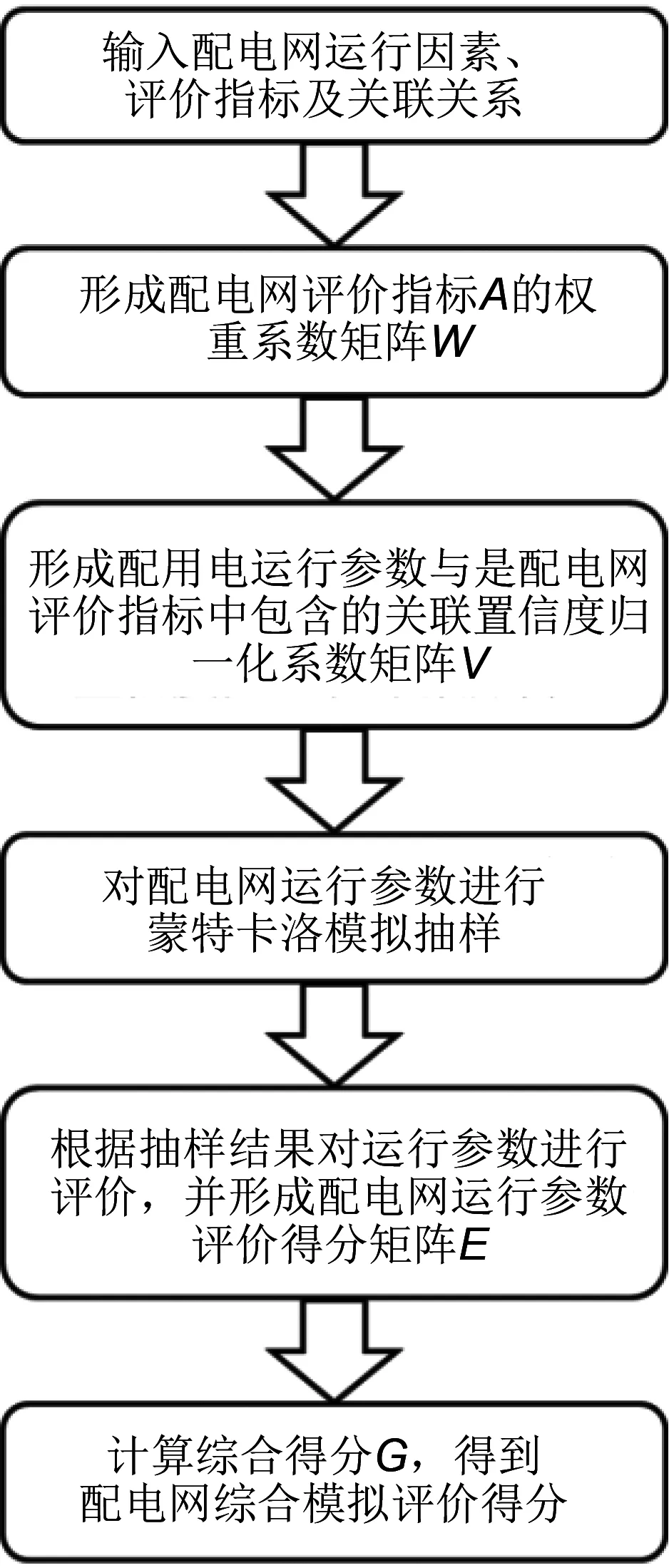
图1 配电网大数据蒙特卡洛矩阵模拟评价体系实现流程图

5 算例实现

以上海电网某供电公司35 kV站下两条10 kV线路“线路1”和“线路2”为例，对影响两条线路评价指标的用户基础运行事件进行蒙特卡洛仿真模拟，并对该线路模糊综合指标评价和比较。

35 kV宝丰站10 kV线路“线路1”共供电8个10 kV用户及149个低压用户，35 kV宝丰站10 kV线路“线路2”共供电1个10 kV用户及32个低压用户。对“供电可靠性”和“供电电压合格率”两大指标进行蒙特卡洛模拟评价，并得到综合评价指标。

选取“熔断器故障”、“欠费停电”、“其他设备故障”、“过负荷”四个基础运行事件，四个基础事件分别在的配电网抢修记录中的支持度作为基础运行事件在总体配电网故障抢修事件中的发生概率，若事件发生则评价得分0，不发生得分1。四个基础事件对于供电可靠性事件(供电恢复时间)和供电电压合格率事件(电压问题)的置信度为基础运行事件与评价指标的关联关系。

以“线路1”和“线路2”两条线路2014—2016年的故障抢修数据为基础进行分析，并采用基于Apriori关联算法的配电网运行大数据关联分析模型对基础运行事件进行关联度计算，整理得到运行事件关联关系如表1所示：

表1 基础运行事件及与综合评价指标支持度和置信度 %

注：1)停电30 min以内设置为事件t00

设置“供电可靠性”和“供电电压合格率”两大运行指标在综合指标中的比例系数分别为75%和25%。则

供电可靠性 评价得分=“熔断器故障 评价得分” × 归一化关联系数+“欠费停电 评价得分” × 归一化关联系数+ “其他设备故障 评价得分” × 归一化关联系数+ “过负荷 评价得分” × 归一化关联系数

供电电压合格率 评价得分=“过负荷 评价得分” × 归一化关联系数

综合评价指标得分= “供电可靠性 评价得分” × 75%+ “供电电压合格率 评价得分” × 25%

对10 kV线路“线路1”下所供8个10 kV用户及149个低压用户和“线路2”下所供1个10 kV用户及32个低压用户的四个基础运行事件分别进行蒙特卡洛模拟，模拟抽样次数设置10 000次，可以分别得到两条线路的综合评价得分为：

G(线路1) =g1(供电可靠性)×0.75+g1(供电电压合格率)×0.25

=86.28×0.75+89.02×0.25

=86.96

G(线路2) =g1(供电可靠性)×0.75+g1(供电电压合格率)×0.25

=88.43×0.75+87.78×0.25

=88.27

从计算结果可以看出，线路“线路2”所供用户少，发生熔断器故障、欠费停电、其他故障等事件概率较低，供电可靠性评价得分较高；供电电压合格率指标略低于线路“线路1”；但在综合评价指标上，线路“线路2”综合评价得分高于线路“线路1”。

如果分别降低四个基础运行事件的发生概率，分别计算综合评价得分，见表2、表3。

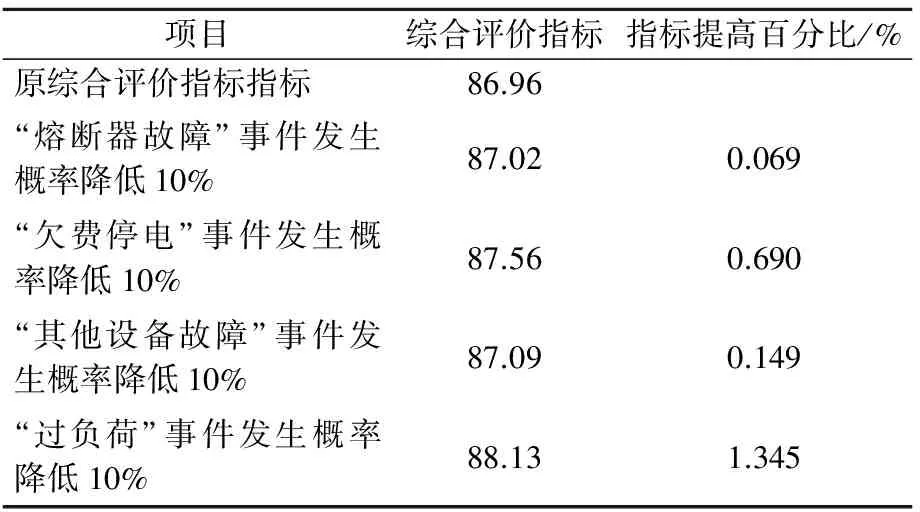
表2 线路“线路1”降低基础运行事件

可以看出，对于线路“线路1”，降低“过负荷”及“欠费停电”发生概率，可以有效地提高配电网综合评价得分；而对于线路“线路2”，降低“过负荷”及“其他设备故障”发生概率，可以有效地提高配电网综合评价得分。

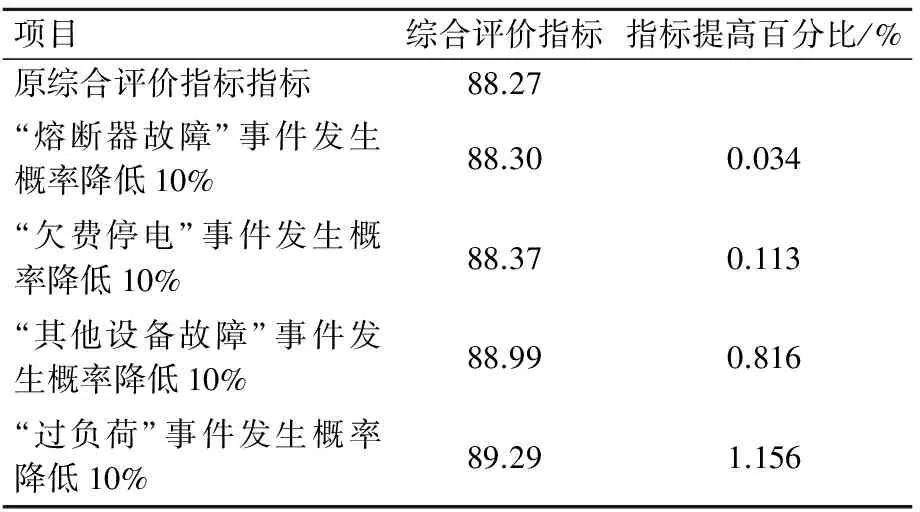
表3 线路“线路2”降低基础运行事件发生概率后评价指标

通过分析可知，针对不同配电网需针对不同的影响因素，各自重点降低相应事件发生概率，可以提高相应供电区域配电网的综合评价得分。

6 结语

采用配电网大数据蒙特卡洛矩阵模拟评价体系对配电网运行指标进行评价，可以分析配电网运行因素对综合评价指标的影响，如通过改变线路负载率或设备检修频率等配电网运行因素，通过分析配电网综合评价指标的变化率，可以分析配电网各运行运维因素对配电网综合评价指标敏感度和影响程度，为配电网运维、提高配电网综合评价指标提供建议。

配电网大数据蒙特卡洛矩阵模拟评价体系还可以对配电网未来的综合指标进行预测，如对于新建的区域电网，对配电网运行各因素按照已有的经验值进行模拟，可对新建电网的综合评价指标进行预测，可以为电网规划提供辅助决策。

[1] 戴晓红,吴征涛,刘沛立,等.基于博弈论和灰色面积关联度的配电网运行安全性评价方法[J].陕西电力,2012,40(4):30-33.

DAI Xiaohong, WU Zhengtao, LIU Peili, et al. Power distribution network operation safety evaluation methods based on game theory and grey relational grades[J].Shanxi Electric Power,2012,40(4):30-33.

[2]谢莹华,王成山.基于馈线分区的中压配电系统可靠性评估[J].中国电机工程学报,2004,24(5):35-39.

XIE Yinghua, WANG Chengshan. Reliability evaluation of medium voltage distribution system based on feeder partition method[J].Proceedings of the CSEE,2004,24(5):35-39.

[3]LI W,WANG P,LI Z,et al. Reliability Evaluation of Complex Radial Distribution Systems Considering Restoration Sequence and Network Constrains [J].IEEE Transactions on Power Delivery,2004,19(2):753-758.

[4]王佳贤.城市配电网经济性评估研究[D].上海:上海交通大学,2008.

[5]刘若溪,张建华,吴迪.基于风险理论的配电网静态安全性评估指标研究[J].电力系统保护与控制,2011,39(15):89-95.

LIU Ruoxi, ZHANG Jianhua, WU Di. Research on static security index of distribution network based on risk theory[J].Power System Protection and Control,2011,39(15):89-95.

[6]刘颖英,徐永海,肖湘宁.地区电网电能质量综合评估新方法[J].中国电机工程学报,2008,28(22):130-136.

LIU Yingying, XU Yonghai, XIAO Xiangning. Analysis of new method on power quality comprehensive evaluation for regional grid[J].Proceedings of the CSEE,2008,28(22):130-136.

[7]肖峻,高海霞,葛少云,等.城市中压配电网评估方法与实例研究[J].电网技术,2005,29(20):77-81.

XIAO Jun, GAO Haixia, GE Shaoyun, et al. Evaluation method and case study of urban medium voltage distribution network[J].Power System Technology,2005,29(20):77-81.

[8]肖峻,王成山,周敏.基于区间层次分析法的城市电网规划综合评判决策[J].中国电机工程学报,2004,24(4):50-57.

XIAO Jun, WANG Chengshan, ZHOU Min. An IAHP-based madm method in urban power system planning[J].Proceedings of the CSEE,2004,24(4):50-57.

[9]李晓辉,张来,李小宇,等.基于层次分析法的现状电网评估方法研究[J].电力系统保护与控制,2008,36(14):57-61.

LI Xiaohui, ZHANG Lai, LI Xiaoyu, et al. The research on the evaluation system for existing network based on analytic hierarchy process and Delphi method[J].Power System Protection and Control,2008,36(14):57-61.

[10]郭金玉,张忠彬,孙庆云. 层次分析法的研究与应用[J]. 中国安全科学学报,2008(5):148-153.

[11]李奎刚,张毕西,刘笑. 层次分析法和鱼骨图在物流企业问题诊断中的应用[J]. 物流技术,2007(11):212-214.

LI Kuigang, ZHANG Bixi, LIU Xiao. Application of AHP and Fish-bone diagram in the diagnosis of logistics enterprise's problems[J].Logistics Technology,2007(11):212-214.

[12]吴丽萍. 模糊综合评价方法及其应用研究[D].太原；太原理工大学,2006.

(本文编辑：杨林青)

Monte Carlo Matrix Simulation Evaluation System for Distribution Network Large Data

FU Xiaofei, LIAO Tianming, JI Kunhua

(State Grid Shanghai Municipal Electric Power Company, Shanghai 200122, China)

A fuzzy comprehensive evaluation system is constructed based on large data analysis of distribution network, Monte Carlo method is used to form Monte Carlo matrix, and the simulation evaluation is carried out. Based on the fuzzy comprehensive evaluation system, the current situation of distribution network is diagnosed, the effect of planning implementation is theoretically tested, providing a strong basis for the distribution network construction. The actual operation data of the power supply line in a Shanghai power supply company is analyzed, and the two power distribution networks are comprehensively evaluated.

fuzzy comprehensive evaluation; Monte Carlo; distribution network large data; data association

10.11973/dlyny201704008

傅晓飞(1980—)，男，工程师，主要从事配电网设备管理、运维及配电自动化工作。

TM74

：A

：2095-1256(2017)04-0401-06

2017-06-21