不同形状振荡浮子入水冲击的实验研究

李 晖，何宏舟，杨绍辉，张 军

（1.集美大学 机械与能源工程学院，福建 厦门 361021；2.福建省能源清洁利用与开发重点实验室，福建 厦门361021；3.福建省清洁燃烧与能源高效利用工程技术研究中心，福建 厦门 361021）

不同形状振荡浮子入水冲击的实验研究

李 晖1,2,3，何宏舟1,2,3，杨绍辉1,2,3，张 军1,2,3

（1.集美大学 机械与能源工程学院，福建 厦门 361021；2.福建省能源清洁利用与开发重点实验室，福建 厦门361021；3.福建省清洁燃烧与能源高效利用工程技术研究中心，福建 厦门 361021）

振荡浮子在波浪能转换装置中应用非常广泛，在其服役期间，由于较小的设计吃水深度或为防避极端海况的需要，它们经常会离开水面；当其再次入水的时候，浮子底部就会受到入水冲击。入水冲击总是伴随着巨大的冲击压强以及冲击载荷，会导致浮子的结构性及疲劳性破坏，从而影响浮子的工作寿命。本文对锥形、半球形和横圆柱形三种形状的浮子入水冲击过程进行了实验研究，分析了浮子表面压强和冲击加速度的变化规律。主要结论如下：（1）在巨大的水阻力作用下，入水瞬间三种浮子表面压强急剧上升，迅速达到最高峰值；之后由于空气垫的作用，压强出现二次峰值现象。（2）在空气垫的作用下，三种浮子的最高压强峰值均未出现在浮子的最低点处，而是出现在外围某处。（3）三种浮子在触水瞬间的加速度均达到hm/s2的量级，而后急剧下降，并在较短时间内达到一平衡值并沿其小幅震荡。（4）横圆柱形浮子由于其非垂直轴对称性，其表面压强和加速度的震荡更加明显。

振荡浮子；入水冲击；实验

发电是波浪能开发利用的主要形式，而作为波浪能发电系统的一级能量转换装置，波浪能采集装置（Wave Energy Converter，简写为WEC）的设计和控制至关重要。在众多型式的WEC中，振荡浮子式WEC因为具有能量转换效率高、安装维修方便、成本低、投放点机动灵活等优点，近年来发展最为活跃。振荡浮子式WEC的关键部件是漂浮于海面上的浮子，浮子在波浪中受波浪力的作用产生运动而具备动能和势能，从而将波浪能转换为机械能。浮子采集的能量通过二级能量转换装置，就可以转换为发电机能够直接利用的机械能。传统上，人们对振荡浮子形状的设计和对其运行的控制往往只着眼于如何提高波浪能吸收效率，却忽视了入水冲击对浮子的严重影响。实际上，由于设计吃水深度较小，浮子在工作过程中经常会升离水面，当它再次入水的时候，其底面就会遭受海水巨大的冲击载荷，即入水冲击。此外，在海上风暴等极端天气下，常常需要主动将浮子升离水面，以免其受到大风浪破坏，这也增加了其再次入水的机会，从而产生入水冲击。入水冲击的特点是局部压力高、持续时间短，易使振荡浮子发生塑性变形和疲劳破坏，影响浮子的工作性能和寿命。因此，在WEC设计阶段优化浮子形状、制定控制策略时，就需要将浮子的入水冲击问题纳入考虑。由于入水冲击对浮子的破坏程度主要以发生于浮子表面的冲击压强和冲击载荷的大小来衡量，因此，利用试验手段来获得冲击压强和冲击载荷等参数的分布信息就显得非常重要。

在物体入水冲击的实验研究方面，由于测量技术的限制，较早的研究主要集中在物体运动以及作用于物体上的垂向力[1-2]。近年来随着粒子图像测速等无侵入实验技术的发展，研究者们已经可以估算冲击力以及在冲击过程中传递给“隆起水体”和“射流”的能量[3]。在振荡浮子的入水冲击研究方面，Backer等[4]对一个半球和两个斜升角不同的锥形体进行了入水冲击实验，测量了对象底面的压力分布和运动参数，发现实验数值明显高于渐近理论的计算结果。Van Nuffel等[5]通过实验研究了刚性圆柱受到波浪冲击时的局部和全局载荷，分析了入水冲击的压力特性和最大冲击载荷发生的时机。Charca等[6]对一个矩形夹芯复合材料试样进行了不同波况下的反复波浪冲击实验，结果发现试样的主要疲劳模式是表面破裂和中心破碎。Van Nuffel等[7]通过分析波浪冲击中影响压力记录的因素，探讨了波浪冲击载荷定量实验难以开展的原因。然而，在已开展的研究中，尚没有针对不同形状浮子的入水冲击参数分布规律进行系统性分析和对比的文献报道。本文以模型实验为手段，研究了锥形、半球形和横圆柱形浮子的入水冲击过程，分析了各形状浮子入水冲击参数的分布规律，并将不同形状浮子的参数分布进行了全面对比，以期为振荡浮子的设计提供参考。

1 实验装置与实验对象

1.1 实验装置

图1所示为振荡浮子入水冲击实验台的设计图（图1（a））与实物图（图1（b）），利用该装置可以进行振荡浮子的自由跌落入水冲击试验。如图所示，装置上端有一个刚性横梁，作为实验对象的振荡浮子被固定在横梁的中部，由“保持和释放机构”控制。“保持和释放机构”由抓手、气压阀和空气压缩机构成，空气压缩机提供的压缩空气，通过软管联通气压阀，为抓手提供气压动力。抓手由手动气压阀控制，当其闭合时抓住浮子；当其打开时，释放浮子。一旦浮子被释放，其将做自由垂直下落，直至进入位于装置下方的水槽中。由于刚性横梁可以沿两个竖直的轨道滑动，因此可以改变浮子的跌落高度，从而得到不同的入水速度，实验中跌落高度可以在0.5～2 m之间变化。水槽宽1.2 m，水深0.6 m。

图1 振荡浮子入水冲击实验装置

1.2 实验对象

本文的实验对象包括一个斜升角为45°的锥形浮子、一个半球形浮子和一个横圆柱形浮子，各浮子设计图如图2所示。浮子模型均由不锈钢材料制成，壁厚0.01 m。由于实验中需要测量浮子入水过程中作用于其表面的局部压强，需要在浮子壁面预留用于安装压力传感器的螺纹孔（简称传感器安装孔），本研究中传感器安装孔的分布主要考虑了以下两点：（1）将孔分布在不同半径位置，以获取尽可能多的局部压力数据；（2）避免安装孔的过近分布，以免造成应力集中和浮子质量分布不均。

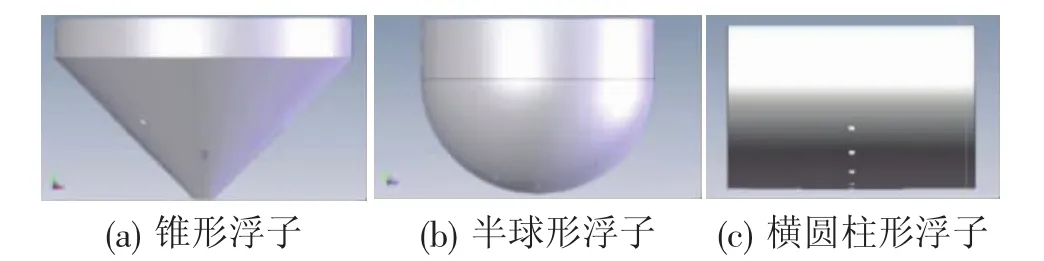
图2 实验对象(浮子)设计图

2 测量仪器

2.1 压力传感器

压力传感器安装于锥体壁面，用于测量入水过程中作用于锥体表面的局部压强。局部压强的测量是一个敏感的过程，有一些因素会影响压强的测量和记录。为了获得较精确的测量结果，实验中应满足以下要求[7]：采用不低于300 kHz的采样频率；保证传感器测量面与锥体表面平齐；避免温度波动；在每次实验前吹干对象表面；在每次实验前等待水面恢复完全静止的状态。基于上述要求，本实验采用了频率为500 kHz，最大量程为5 MPa的CJGP-1型压力传感器（生产厂家：西安创金电子科技有限公司），如图3所示。此外，考虑到传感器直径过大有可能造成压强峰值的位置偏离，本实验的传感器直径限制为0.01 m。各浮子模型的传感器安装位置将在后文给出。

2.2 加速度计

用于测量冲击载荷的传感器是加速度计。本实验采用了YD-81D型加速度计（生产厂家：上海铸瑞自动化科技有限公司），如图4所示。其量程为100 g，共振频率为40 kHz。该型加速度计由检测质量（敏感质量）、支撑、电位器、弹簧、阻尼器和壳体组成，其参考质量通过弹性细杆与壳体相连，加速度引起的动载荷使得细杆发生变形，用应变电阻感应细杆变形的大小，即可测量出加速度。由于加速度计所输出的电信号比较微弱，实验中采用了DHF-7型电荷放大器来对加速度计输出电信号进行放大，如图5所示。

图3 本文实验所用的压力传感器

图4 加速度计

图5 电荷放大器

2.3 数据采集

为了采集和处理所测数据，实验中采用了PCI8532数据采集卡和ART软件。PCI8532具有4路同步模拟量输入，当只有一路信号输入的时候，采样频率可达20 MHz，当四路输入同时工作的时候，每路采样频率为5 MHz。ART是PCI8532采集卡所配的软件包，可以完成数据的显示和处理。

3 实验流程

图6所示为振荡浮子入水冲击实验系统的总体示意图，实验时，首先使用空气压缩机压缩空气，形成一定的气压，以控制抓手打开或关闭。通过转动装置手柄，调整横梁在竖直轨道上的位置，直到浮子距离水面的高度达到需要值（本次实验取2 m）。打开气压阀，抓手释放浮子，浮子做自由落体运动，垂直落入水中。在浮子开始下落时数据采集卡同时采集数据；待浮子浮上水面，采集卡停止采集数据。

图6 振荡浮子入水冲击实验系统示意图

4 实验结果分析

4.1 锥形浮子实验结果分析

4.1.1 压强 图7所示为斜升角为45°的锥形浮子壁面压力传感器安装孔的位置分布图，其中孔1是锥体顶点，孔2、孔3、孔4、孔5则分散分布在锥体的不同半径上。

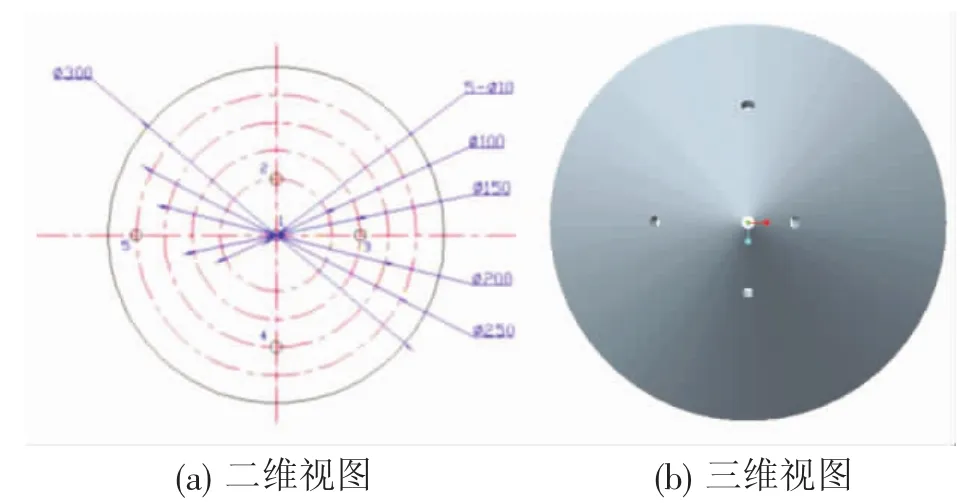
图7 斜升角45°锥形浮子壁面压力传感器安装孔位置分布示意图

斜升角为45°的锥形浮子表面各测量点局部压强的时历曲线如图8所示。如图所示，在锥体入水之前，5个测点的压强均在大气压（相对压强0 Pa）附近小幅震荡。在锥顶点触水之后，位于锥顶点的测点1的压强急剧上升，率先达到压力峰值32 067 Pa，而后迅速回落至约9 903 Pa，又二次急剧上升至一个次峰值25 620 Pa，经过约20 ms左右回落至大气压附近并持续小幅震荡。测点2在测点1之后达到压强峰值，其峰值为47 700 Pa，比测点1峰值高出约48.7%；在达到主峰值后震荡回落，没有较明显的次峰值，但有较明显的二次峰值，约65 ms后回落至大气压附近并以较明显的振幅持续震荡。测点3在测点2之后达到压强峰值，其峰值约为53 848 Pa，比测点2峰值高出约12.9%；在达到主峰值后回落，约10 ms后达到一个很明显的次峰值约32 982 Pa，又经过两个较明显的二次峰值之后在5 000 Pa左右持续小幅震荡。测点4在测点3之后达到压强峰值，其峰值约为78 815 Pa，比测点3峰值高出约46.4%；而后急剧下落，约27 ms后达到次峰值约17 163 Pa，又经过一个较明显的二次峰值之后在10 000 Pa左右持续小幅震荡。测点5在测点4之后达到压强峰值，其峰值约为25 575 Pa，比测点4峰值低约67.6%；而后急剧下落，约10 ms后达到次峰值约16 541 Pa，之后回落至大气压以下并持续震荡。

由图8可以看出：（1）随着入水深度的增加，测点1，2，3，4，5依次迅速达到压强主峰值，在几十毫秒内回落至一个平衡值并持续震荡。（2）绝大部分测点的压强在达到主峰值之后，还会出现次峰值和二次峰值，并且随时间逐渐变弱。（3）最大压强并非出现在锥顶点，而是出现在远离锥顶点的测点4位置。现对上述现象做简要分析：压强峰值的转移是由于入水深度的增加和入水体速度的减小所致。根据现有文献，压强峰值总是出现于锥体表面和水面的交界处，也即射流根处。在该处水被压缩，并且一部分水体从主水体中分离出来，形成沿锥体表面喷射的射流。最终射流将离开锥体表面，锥表面压强的波动也就此消失。而最大压强峰值的出现位置和二次压强峰值的出现主要与空气垫有关[5-8]，空气垫是入水物体和水之间的一层空气，当物体入水时，有一部分空气来不及逃逸，被限制在物体底面和水之间的狭小空间内，形成空气垫。一方面，可压缩的空气层使得局部压力峰值减小并使得冲击压力的持续时间延长。在本文实验中，由于空气层主要存在于锥体底面的小区域内，因此可能存在空气垫的测点1，2，3位置的压强峰值较小（但三者数值依次增大），而测点4的压强峰值则要大得多。另一方面，空气层周期性的压缩和膨胀对测量点的压强产生影响，于是导致了各个测点处二次压强峰值的形成。Lin和Shieh[8]在横圆柱体入水冲击实验中也观察到了类似的现象，他们认为这些二次压强振荡是由于在入水冲击之初形成于横圆柱体底部的空气垫的周期性压缩和膨胀造成的。这个观点随后被Van Nuffel等的实验证实[5]。

图8 斜升角45°锥形浮子表面局部压强时历曲线图

4.1.2 加速度 图9显示了被测锥体入水过程中的加速度时历曲线。由于本实验中被测对象近似视为刚体，因此所有被测位置点的加速度具有相同的数值。由图9可以观察到，在锥体触水之前，其方向始终向下，并且保持着重力加速度的数值（约-10 m/s2）；在锥体与水接触的瞬间，加速度迅速反向，并且剧烈增至272.9 m/s2，然后振荡回落，并在约110 ms后回落至18.3 m/s2并在该值附近小幅震荡。加速度的剧增是由于水的巨大阻力所致，而随后的震荡则是由于冲击造成的水体晃动以及浮子本身的结构性震动而形成。

图9 斜升角45°锥形浮子加速度时历曲线图

在入水冲击过程中，作用在锥体上的Y方向上的作用力有两个，一个是向下的重力mg（m为锥体质量，g为重力加速度），另一个是向上的冲击载荷，记为Fimpact。如果已知加速度a，那么作用于锥体的冲击载荷就可以由牛顿第二定律得出：Fimpact=m(a+g)。显然，冲击载荷与浮子质量和冲击加速度有密切关系。本实验中锥形浮子的质量约为1.3 kg，因此其所受的最大入水冲击载荷为342 kN。在毫秒量级时间内受到百kN量级的冲击载荷，意味着浮子有可能由于冲击而受到破坏。

4.2 半球形浮子实验结果分析

4.2.1 压强 图10所示为半球形浮子壁面压力传感器安装孔的位置分布图，其中孔1位于半球形浮子底面最低点处，孔2和孔3在同一半径对称分布，孔4、孔5则分散分布在半球体的不同半径上。

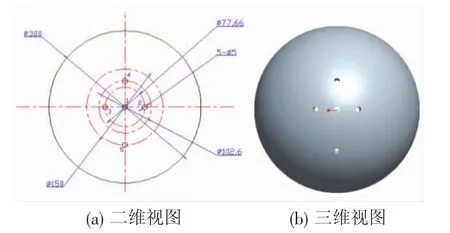
图10 半球形浮子壁面压力传感器安装孔位置分布示意图

半球形浮子表面各测量点局部压强的时历曲线如图11所示。与锥形浮子的压力曲线趋势相似，半球形浮子的表面压强也具有以下几个特点：（1）在入水之前，5个测点的压强均在大气压（相对压强0 Pa）附近小幅震荡。（2）在浮子触水之后，位于最低点的测点1的压强急剧上升，率先达到峰值，之后测点2，3，4，5依次达到压强峰值，其中测点1，2，3，4的压强峰值依次增大（测点2，3由于对称分布，曲线非常靠近，且趋势相近），测点4达到最大压强峰值；而测点5的压强峰值则最小。各测点压强的主峰值分别是：51 044 Pa，56 640 Pa，67 242 Pa，75 415 Pa和44 723 Pa。（3）各测点的压强均有二次峰值出现。（4）在经过足够长时间之后，各测点的压强回落至大气压附近小幅震荡。可以看出，半球形浮子表面压强的分布特点与锥形浮子非常类似，因此可以用同样的原因进行解释，在此不再赘述。

值得指出的是，与锥形浮子相比，半球形浮子的测点压强主峰值略低（如，前者测点4的主峰值为78 815 Pa，而后者为75 415 Pa）；另外，半球形浮子的“压强峰值持续时间”比锥形浮子更短（同样以测点4为例，前者从主峰值到次峰值的时间约为27 ms，而后者仅为10 ms），因此各曲线尖峰显得更加尖锐。这可以从空气垫角度来进行解释，由于半球体比斜升角为45°的锥体更容易捕获空气，因此空气垫对半球体的作用要更加明显。空气垫的缓冲作用使得半球形浮子的表面压强峰值更低，也使得其二次压强效应更加明显。

4.2.2 加速度 图12显示了被测半球形浮子入水过程中的加速度时历曲线。与锥形浮子相似，在半球体触水之前，其始终保持着重力加速度的数值，触水之后加速度剧烈增至约358.8 m/s2，然后迅速回落，并在约100 ms后回落至-5 m/s2并在该值附近小幅震荡。可以看出，半球形浮子比锥形浮子具有更高的加速度峰值，前者比后者高出约31.8%。

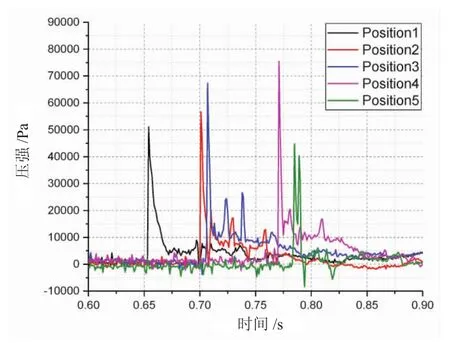
图11 半球形浮子表面局部压强时历曲线图

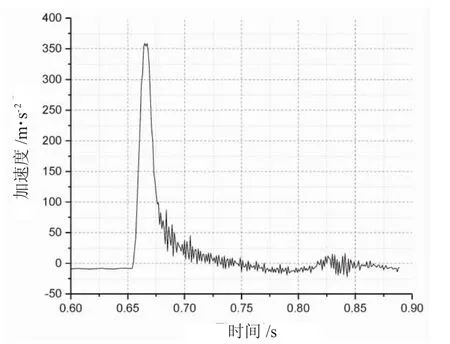
图12 半球形浮子加速度时历曲线图

4.3 横圆柱形浮子实验结果分析

4.3.1 压强 图13所示为横圆柱形浮子壁面压力传感器安装孔的位置分布图，其中孔1位于横圆柱形浮子底面最低点处，孔2和孔3、孔4和孔5为两组对称分布点，分散分布在横圆柱体的不同斜升角处。

图13 横圆柱形浮子壁面压力传感器安装孔位置分布示意图

横圆柱形浮子表面各测量点局部压强的时历曲线如图14所示。横圆柱形浮子的表面压强具有以下几个特点：（1）在入水之前，5个测点的压强均在大气压（相对压强0 Pa）附近震荡。（2）在浮子触水之后，各测点的压强急剧上升达到压力峰值，测点1，2，3，4，5的压强主峰值分别是：24 483 Pa，47 109 Pa，56 730 Pa，31 077 Pa和51 998 Pa。（3）除测点2外，各测点的二次压强峰值并不明显。（4）在经过足够长时间之后，各测点的压强回落至大气压附近小幅震荡。测点2和测点3虽为关于横圆柱轴心线的对称分布点，但两者的压强时历曲线并不完全相同，不仅主峰值大小不同，曲线趋势也不尽相同。但是，二者曲线尖峰都很尖锐，意味着峰值持续时间较短。同样地，测点4和测点5也是对称分布点，虽然曲线趋势不同，但峰值持续时间比测点2和测点3明显加长。

横圆柱形浮子表面压强的分布，较之锥形与半球形浮子，规律性不太明显。这可能是由于横圆柱相比于前两者并不具有垂直轴对称性，因此在下落时容易造成摆动和位置偏移所致。但仍然可以看出，横圆柱形浮子的最大压强峰值56 730 Pa要明显小于前两者。另外，随着测点所在位置斜升角的增大，压强曲线的尖锐度变低，也即压强峰值持续时间延长。

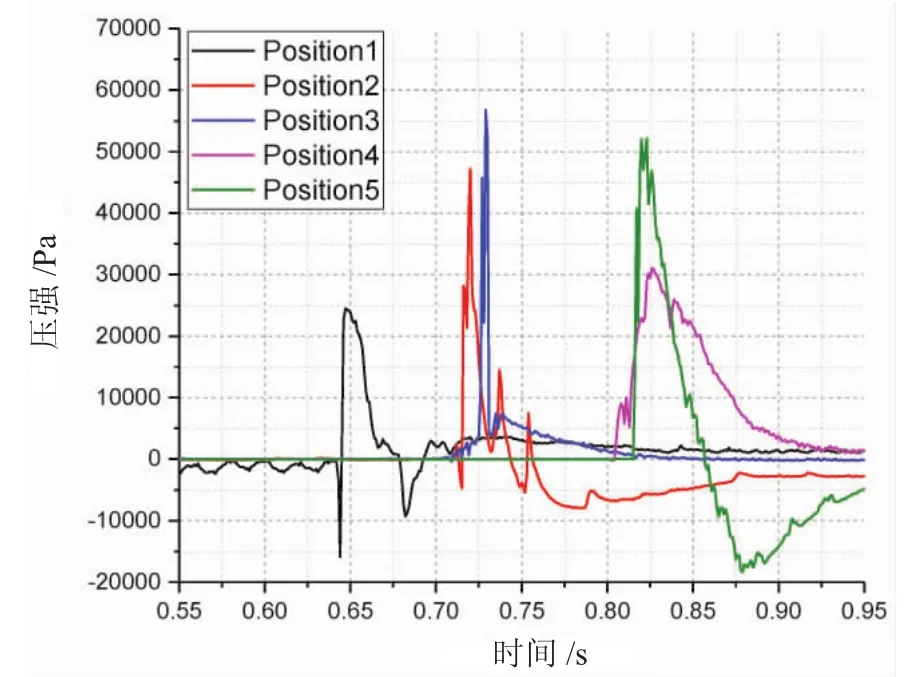
图14 横圆柱形浮子表面局部压强时历曲线图

4.3.2 加速度 图15显示了被测横圆柱形浮子入水过程中的加速度时历曲线。与锥形和半球形浮子相比，横圆柱体在触水之后的加速度震荡更加剧烈，但其加速度峰值145 m/s2则远小于前两者。

4.4 三种形状浮子的实验结果比较和分析

4.4.1 压强 从上文的试验结果分析可以看出，三种形状浮子在落水瞬间，其表面局部压强均会急剧上升并迅速达到最高峰值，这显然是由于浮子急速下落时受到水的巨大阻力所致。其后，压强以震荡形式持续下落，并在过程中出现一系列二次峰值，这是由于浮子底面和水面之间的空气层的周期性膨胀和压缩所致。值得注意的是，由于空气垫的缓冲作用，三种浮子的最高压强峰值均未出现在浮子的最低点处，而是出现在离最低点有一定距离的外围某处。就本文实验所设定的测点而言，三种形状浮子的最高压强峰值排序从大到小依次是：锥形、半球形、横圆柱形。需要指出，由于三种浮子的压强测点数目有限，且设置位置各不相同，上述关于最高压强峰值的排序并不具有普适性。另外，三种浮子的压强峰值持续时间也有所不同，锥形浮子的压强峰值持续时间明显长于半球形浮子，但横圆柱形浮子的压强峰值持续时间随测点所在位置的斜升角而有明显变化。

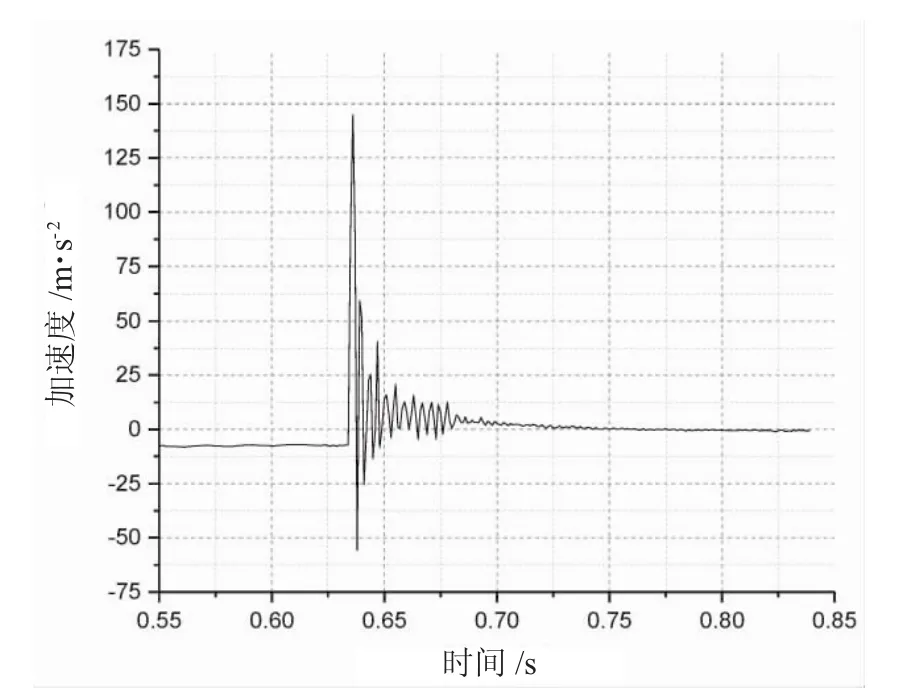
图15 横圆柱形浮子加速度时历曲线图

4.4.2 加速度 就刚性浮子的加速度而言，三种形状浮子的加速度都在其触水瞬间达到百m/s2的量级，而后急剧下降，并在较短时间内达到一平衡值并沿其小幅震荡。加速度的剧增是由于水的巨大阻力所致，而之后的震荡则是由于冲击造成的水体晃动以及浮子本身的结构性震动而形成。本实验中锥形浮子的质量均在1 kg以上，意味着浮子所受的最大入水冲击载荷均达到百kN量级。在毫秒量级时间内受到百kN量级的冲击载荷，意味着浮子很有可能由于冲击而受到破坏。三种形状浮子的加速度峰值排序从大到小依次是：半球形、锥形、横圆柱形。需要注意的是，锥形和半球形浮子的加速度时历曲线趋势非常相近，但横圆柱形浮子在到达最高峰值后经历的震荡比前两者更剧烈，这是由于横圆柱形浮子的非轴对称性所致。

5 结论

入水冲击会造成振荡浮子式WEC的关键部件——振荡浮子的疲劳性及结构性破坏，本文对锥形、半球形和横圆柱形等三种形状的浮子入水冲击过程进行了实验研究，分析了浮子表面压强和冲击加速度的变化规律。主要结论如下：

（1）三种形状浮子入水瞬间在巨大的水阻力作用下，其表面压强均急剧上升，迅速达到最高峰值；之后由于空气垫的作用，压强出现二次峰值现象。

（2）在空气垫的作用下，三种浮子的最高压强峰值均未出现在浮子的最低点处，而是出现在最低点外围某处。

（3）三种浮子的加速度都在其触水瞬间达到百m/s2的量级，而后急剧下降，并在较短时间内达到一平衡值并沿其小幅震荡。

（4）与另外两种浮子相比，横圆柱形浮子由于其非垂直轴对称性，其表面压强和加速度的震荡更加明显。

[1]Luo H,Wang H,Soares C G.Numerical and experimental study of hydrodynamic impact and elastic response of one free-drop wedge with stiffened panels[J].Ocean Eng,2012,40:1-14.

[2]Panciroli R,Abrate S,Minak G.Dynamic response offlexible wedges enteringthe water[J].Compos Struct,2013,99:163-171.

[3]Andrea LFacci,RiccardoPanciroli,StefanoUbertini,et al.Assesment ofPIV-based analysis ofwater entryproblems through synthetic numerical datasets[J].J Fluid Structure,2015,55:484-500.

[4]Backer G,Vantorre M,Beels C,et al.Experimental investigation ofwater impact on axisymmetric bodies[J].Applied Ocean Research, 2009,31:143-156.

[5]Van Nuffel D,Vepa K,Van Paepegem W,et al.A comparison between the experimental and theoretical impact pressures acting on a horizontal quasi-rigid cylinder duringvertical water entry[J].Ocean Engineering,2014,77:42-54.

[6]Charca S,Shafiq B,Just F.Repeated slamming ofsandwich composite panels on water[J].Journal ofSandwich Structures&Materials, 2009,11(5):409-424.

[7]Van Nuffel D,Vepa K,De Baere I,et al.Study on the parameters influencing the accuracy and reproducibility of dynamic pressure measurements at the surface ofa rigid bodyduringwater impact[J].Ocean Engineerin,2014,77:42-54.

[8]Lin MC,Shieh L D.Flow visualization and pressure characteristic sofa cylinder for water impact[J].Appl Ocean Res.1997,19(2): 101-112.

Experimental Study of the Water Entry Impact on Oscillating Buoys with Different Shapes

LI Hui1,2,3,HE Hong-zhou1,2,3,YANG Shao-hui1,2,3,ZHANG Jun1,2,3
1.College of Mechanical and Energy Engineering,Jimei University,Xiamen 361021,Fujian Province,China;
2.Fujian Province Key Laboratory of Cleaning Energy Utilization and Development,Xiamen 361021,Fujian Province,China;
3.Fujian Engineering Technology Research Center of Clean Combustion and Efficient Use of Energy,Xiamen 361021,Fujian Province,China

Oscillating buoys have been widely adopted in wave energy converters.During their service period, they may often rise out of the water for some reasons in the cases that they are designed with a small draft or being lifted to avoid extreme seas conditions.Therefore,it is normal for them to be subjected to bottom slamming upon its reentering the water.Bottom slamming,known as water entry impact,is typically associated with large impact pressures and forces which may lead to serious fatigue and structural damage to the buoys and shorten their working lives.In this paper,the water entry impact of buoys in conical,hemispherical and horizontally placed cylindrical shapes is respectively studied with experiments,and the variation of surface pressure and impact acceleration are analyzed,resulting in the main conclusions as follows:(1)The surface pressure of all the three types of buoys rose sharply at the moment of contacting water due to the huge water resistance and quickly reached a peak value;secondary peaks occurred afterwards because of the air bag effects.(2)The peak pressure didn't occur at the lowest point of the buoys'surface,but appeared in the periphery somewhere.(3)At the instant of water entry,the accelerations of all the three types of buoys increased sharply to the order of 100 m/s2,and then declined to an equilibrium value in a short duration.(4)Due to its non-axial symmetry,compared with the other two types of buoys,the horizontally placed cylindrical buoy possesses more obvious oscillations in its surface pressure and acceleration.

oscillating buoy;water entry impact;experiment

P743.2

A

1003-2029（2017）04-0034-08

10.3969/j.issn.1003-2029.2017.04.007

2017-04-10

国家自然科学基金资助项目（51409118）；福建省自然科学基金资助项目（2014J05062）；福建省教育厅资助科技项目（JA13184）

李晖（1974-），女，博士，副教授，主要研究方向为海洋可再生能源开发与利用。E-mail:judy.lh@163.com