ESTIMATION OF GROWTH OF MEROMORPHIC SOLUTIONS OF SECOND ORDER ALGEBRAIC DIFFERENTIAL EQUATIONS
2017-09-15ZHANGJianjunYUANWenjun
ZHANG Jian-jun,YUAN Wen-jun
(1.School of Mathematics and Information Technology,Jiangsu Second Normal University, Nanjing 210013,China)
(2.School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China)
ESTIMATION OF GROWTH OF MEROMORPHIC SOLUTIONS OF SECOND ORDER ALGEBRAIC DIFFERENTIAL EQUATIONS
ZHANG Jian-jun1,YUAN Wen-jun2
(1.School of Mathematics and Information Technology,Jiangsu Second Normal University, Nanjing 210013,China)
(2.School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China)
In this paper,we investigate the growth order of meromorphic solution of algebraic dif f erential equations.By using normal family theory,we give an estimation of the growth order of meromorphic solutions of certain class of second order algebraic dif f erential equations,which depend on the degrees of rational function coefficients of the equations,and generalize a result by Liao Liangwen and Yang Chungchun(2001).
algebraic dif f erential equations;meromorphic functions;growth order
1 Introduction
Let f(z)be a function meromorphic in the complex plane C.We assume that the reader is familiar with the standard notations and results in Nevanlinna’s value distribution theory of meromorphic functions(see e.g.[1-3]).We denote the order of f(z)by ρ(f).
As one knows,it was one of the important topics to research the algebraic dif f erential equation of Malmquist type.In 1913,Malmquist[4]gave a result for the f i rst order algebraic dif f erential equations.In 1933,Yosida[5]proved the Malmquist’s theorem by using the Nevanlinna theory.In 1970s,Laine[6],Yang[7]and Hille[8]gave a generalization of Malmquist’s theorem.Later,Steinmetz[9],Rieth[10]and He-Laine[11]all gave corresponding generalizations of Malmquist’s theorem for the f i rst order algebraic dif f erential equations. In 1980,Gackstatter and Laine[12]gave a generalized result of Malmquist’s theorem for some certain type of higher order algebraic dif f erential equations.However,Malmquist type theorem for an arbitrary second order algebraic dif f erential equation remains open.For a second
order algebraic dif f erential equation

where R is a rational function in z,f and f′,a classical and unsolved conjecture is the following.
Conjecture 1.1(see[3])If equation(1.1)has a transcendental meromorphic solution, then the equation can be reduced into the form
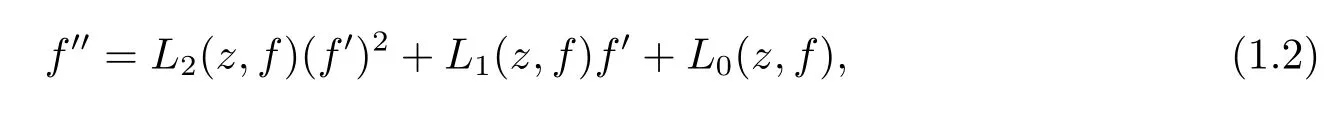
where Li(z,f)(i=0,1,2)are rational functions in their variables.
In 2011,Gao,Zhang and Li[13]studied the problem of growth order of solutions of a type of non-linear algebraic dif f erential equations.In 2001,Liao and Yang[14]considered the f i nite order of growth of the meromorphic solutions of equation(1.2)and obtained the following result.
Theorem ALet f be a meromorphic solution of equation(1.2).Further assume that L2(z,f)6≡0 in equation(1.2)and has the form

where ai(z),bj(z)(s≤i≤n,r≤j≤m)are rational functions.If m-n<1 or r-s>1, then ρ(f)<∞.
RemarkThe conditions m-n<1 and r-s>1 in Theorem A cannot be omitted simultaneously.Liao and Yang[14]gave a simple example to show it.
The paper is organized into 3 sections.After introduction some basic concepts and lemmas will be given in Section 2.In Section 3,we will give the main results.
2 Preliminaries
Let D be a domain in C.We say that a family F of meromorphic functions in D is normal,if each sequence{fn}⊂F contains a subsequence which converges locally uniformly by spherical distance to a meromorphic function g(z)in D(g(z)is permitted to be identically inf i nity).In this paper,we denote the spherical derivative of meromorphic function f(z)by f](z),where
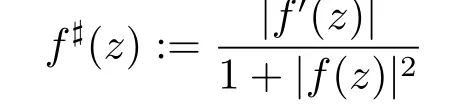
and def i ne
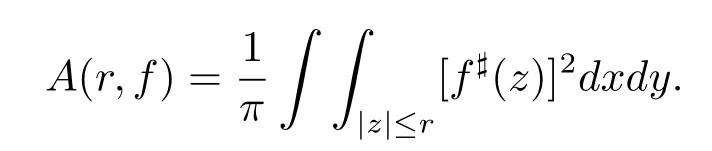
For convenience,we still assume thatrewrite equation(1.2)into

where M(z,f)=Q(z,f)L1(z,f),N(z,f)=Q(z,f)L0(z,f),P,Q are de fi ned as in Theorem A.

We denote the largest number of the degrees at inf i nity of all the rational function coefficients in variable z concerning L(z,f)by degz,∞L(z,f).Denoting
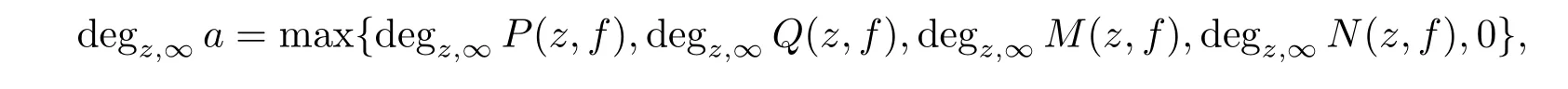
where P(z,f),Q(z,f)are two polynomials in f with rational function coefficients,M(z,f) and N(z,f)are rational functions in variable z and f.
The following lemmas will be needed in the proof of our results.Lemma 2.1 is a result of Zalcman concerning normal families.
Lemma 2.1(see[15])Let F be a family of meromorphic functions on the unit disc,α is a real number.Then F is not normal on the unit disc if and only if there exist,for each -1<α<1,
a)a number r,0<r<1;
b)a sequence points{wk},|wk|<r; c)a sequence{fk}k∈N⊂F;
d)a positive sequence{ρk},ρk→0
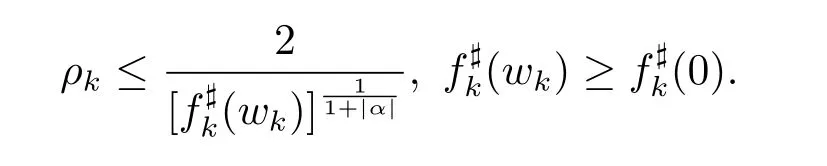
The next lemma is a generalization of the Lemma 2 in[16]of Yuan et al.
Lemma 2.2Let f(z)be meromorphic in the complex plane,ρ:=ρ(f)>2,then for any positive constants ε>0 and 0<λ<,there exist points zk→∞(k→∞),such that
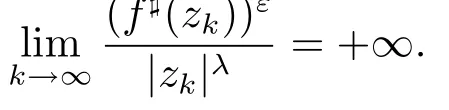
ProofSuppose that the conclusion of Lemma 2.2 is not true,then there exist a positive number M>0,such that for arbitrary z∈C,we have
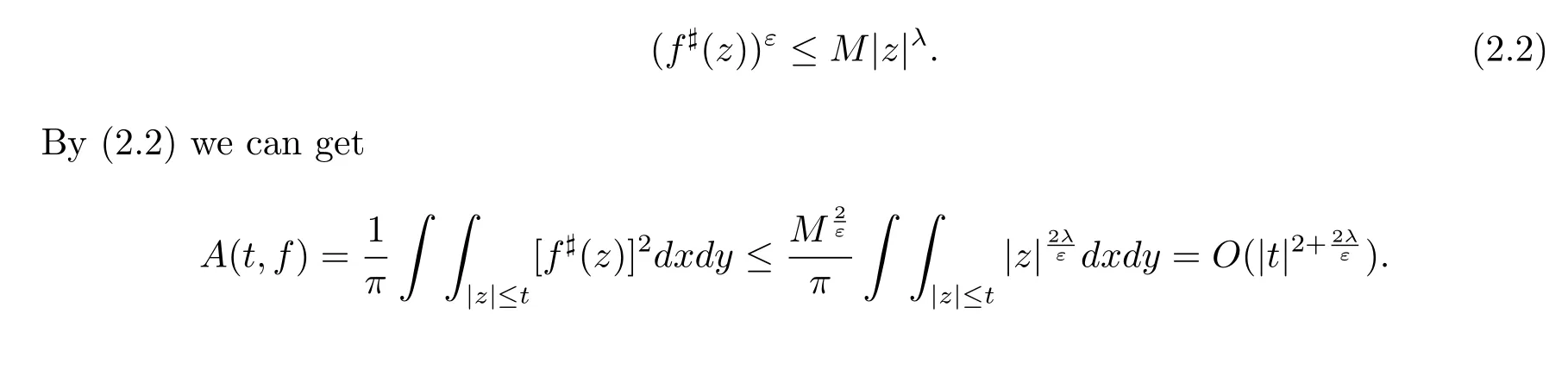
Thus we obtain an estimation of Ahlfors-Shimizu characteristic function
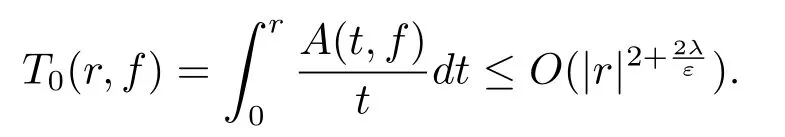
Therefore,the order of f(z)can be estimated as ρ≤2+,namely,λ≥This is a contradiction with the choice of λ.
Lemma 2.3(see[17])Let f(z)be holomorphic in the complex plane,σ>-1.If f](z)=O(rσ),then T(r,f)=O(rσ+1).
The result of Lemma 2.4 is more sharper than Lemma 2.2 when f(z)is an entire function.
Lemma 2.4Let f(z)be holomorphic in the complex plane,ρ:=ρ(f)>1,then for any positive constants ε>0 and 0<λ<(ρ-1)ε,there exist points zk→∞,as k→∞, such that

ProofSuppose that the conclusion of Lemma 2.4 is not true,then there exist a positive number M>0,such that for arbitrary z∈C,we havenamely,.By Lemma 2.3,we have

Therefore the order of f(z)can be estimated as ρ≤1+λε,namely,λ≥(ρ-1)ε.This is a contradiction with the choice of λ.
3 Main Results
We are now giving our main results as follows.
Theorem 3.1Let f be a meromorphic solution of equation(2.1).Further assume that6≡0 in equation(2.1),M(z,f)6≡0,N(z,f)6≡0 are birational functions and have following forms
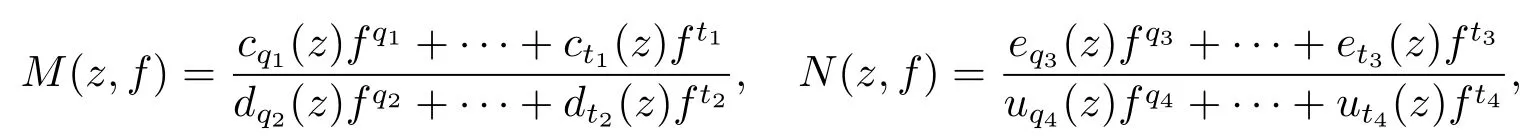
where cj1(z)(t1≤j1≤q1),dj2(z)(t2≤j2≤q2),ej3(z)(t3≤j3≤q3)and uj4(z)(t4≤j4≤q4)are rational functions,ct1(z)6≡0,dt2(z)6≡0,et3(z)6≡0 and ut4(z)6≡0,then

By Lemma 2.2 we know that forthere exist points zk→∞,as k→∞,such that

This implies that the family{f(zk+z)}k∈Nis not normal at z=0.Then by Lemma 2.1, there exist a sequence{βk}and a positive sequence{ρk}such that

and gk(ζ):=converges locally uniformly to a nonconstant meromorphic function g(ζ).In particular,we may choose βkand ρk,such that
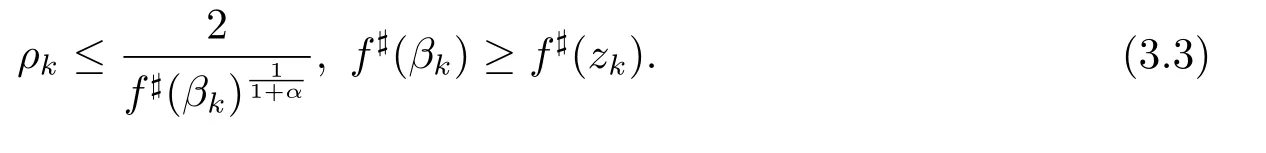
According to(3.1),(3.2)and(3.3),we can get the following conclusion.
For positive constant α and any constant 0≤λ<we have

Substituting βk+ρkζ for z in(2.1),we have
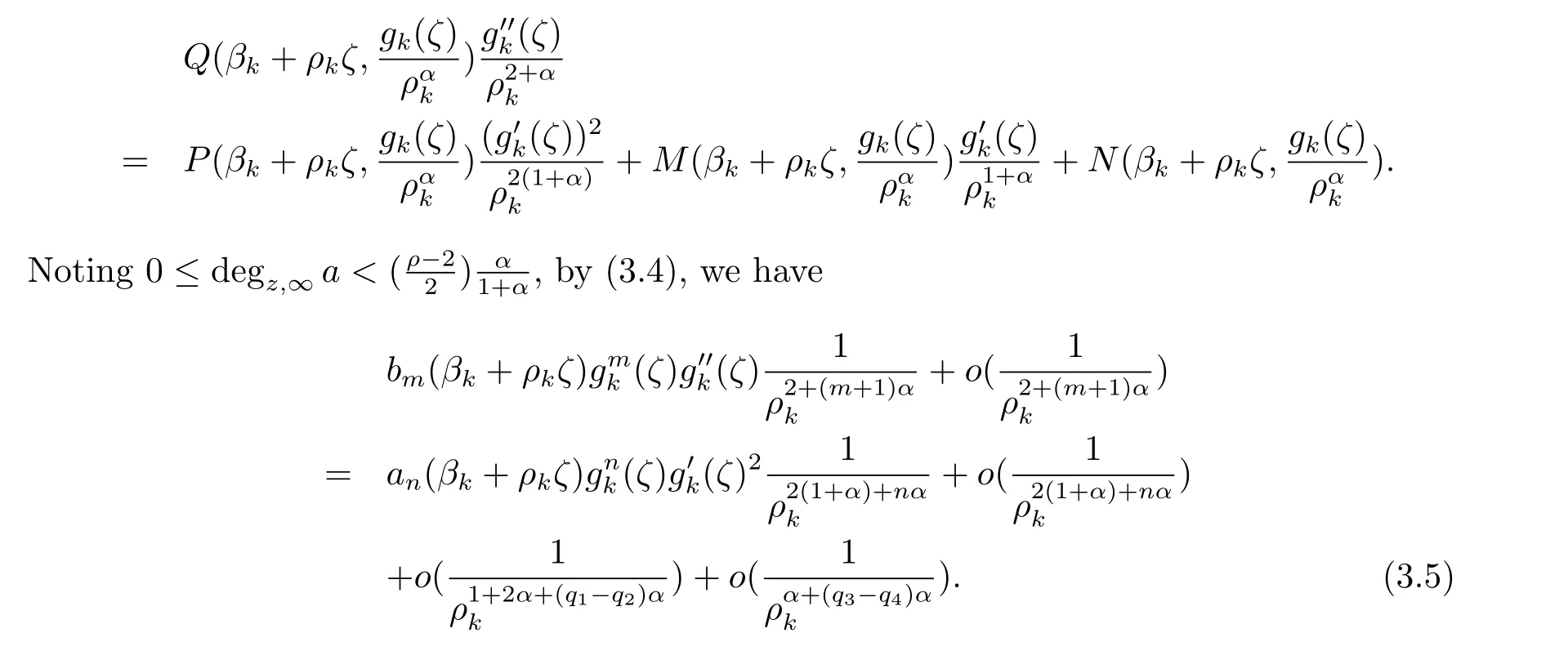
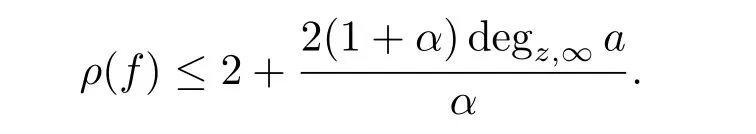
Case 2 r-s>1.We choose α such that 0<α<minand assume that

Then there exist a sequence{βk}and a positive sequence{ρk}satisfying

such that hk(ζ)=ρ-αkf(βk+ρkζ)converges locally uniformly to a nonconstant meromorphic function h(ζ).By similar argument as in Case 1,we can obtain

Hence h is a constant,which is a contradiction.Thus we have completed the proof of Theorem 3.1.
Similarly,from the proof of Theorem 3.1 and Lemma 2.4,we have
Corollary 3.2Let f be an entire solution of equation(2.1).Further assume that≡0 in equation(2.1),M(z,f)6≡0,N(z,f)6≡0 are birational functions and have the forms
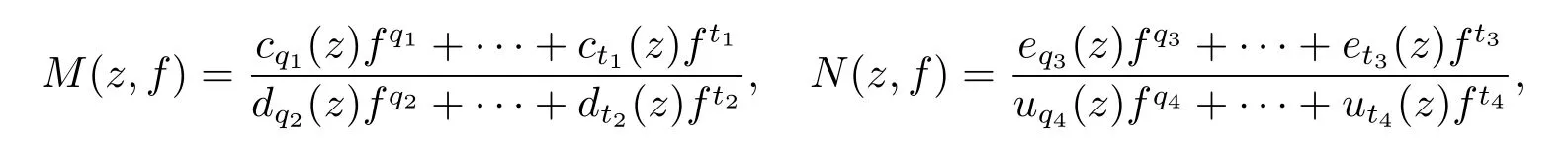
where cj1(z)(t1≤j1≤q1),dj2(z)(t2≤j2≤q2),ej3(z)(t3≤j3≤q3)and uj4(z)(t4≤j4≤q4)are rational functions,ct1(z)6≡0,dt2(z)6≡0,et3(z)6≡0,ut4(z)6≡0,then

-s>1
.
Remark In Theorem 3.1 and Corollary 3.2,if m-n<1,M(z,f)≡0 and N(z,f)6≡0, then for arbitrary 0<α<minthe results of Theorem 3.1 and Corollary 3.2 are also true.Similarly,if m-n<1,M(z,f)6≡0 and N(z,f)≡0,then we may choose any 0<α<min{}.If r-s>1,M(z,f)≡0 and N(z,f)6≡0,then we may choose any 0<α<min{,1}.If r-s>1,M(z,f)6≡0 and N(z,f)≡0,then we may choose any 0<α<min{,1}.If M(z,f)=N(z,f)≡0,m-n<1 or r-s>1, then we may choose any 0<α<1.
ExampleThere exists the entire function f(z)=ezn(n≥1)such that it is of order n and satis fi es the following second-order di ff erential equation

where degz,∞a=2(n-1)and 0<α<1,then the order of any meromorphic solution f of equation(3.6)can be estimated as ρ(f)≤2+and the order of any entire solution f of equation(3.6)can be estimated as ρ(f)by Theorem 3.1 and Corollary 3.2,respectively.In particular,the estimation of growth order of entire solution is sharp when n=1.
[1]Cherry W,Ye Z.Nevanlinna’s theory of value distribution[M].Monogr.Math.,Berlin:Springer-Verlag,2001.
[2]Hayman W K.Meromorphic functions[M].Oxford:Clarendon Press,1964.
[3]Laine I.Nevanlinna theory and complex dif f erential equations[M].Berlin,New York:Walter de Gruyter,1993.
[4]Malmquist J.Sur les fonctions`a un nombre f i ni des branches d´ef i nies par les´equations dif f´erentielles du premier ordre[J].Acta Math.,1913,36:297-343.
[5]Yosida K.A generalisation of Malmquist’s theorem[J].J.Math.,1932,9:253-256.
[6]Laine I.On the behavior of the solutions of some f i rst order dif f erential equations[J].Ann.Acad. Sci.Fenn.Ser.A,1971,497:1-26.
[7]Yang Chungchun.A note on Malmquist’s theorem on f i rst order dif f erential equations[J].Yokohama Math.J.,1972,20(2):115-123.
[8]Hille E.On some generalizations of the Malmquist theorem[J].Math.Scand.,1976,39:59-79.
[9]Steinmetz N.Eigenschaften eindeutiger L¨osungen gew¨ohnlicher dif f erentialgleichungen in komplexen[D].Karlsruhe:Dissertation,1978.
[10]Rieth J V.Untersuchungen gewisser Klassen gew¨ohnlicher dif f erentialgleichungen erster und zweiter ordnung im komplexen[D].Aachen:Doctoral Dissertation,Technische Hochschule,1986.
[11]He Y Z,Laine I.The Hayman-Miles theorem and the dif f erential equation(y0)n=R(z,y)[J].Anal., 1990,10(4):387-396.
[12]Gackstatter F,Laine I.Zur theorie der gew¨ohnlichen dif f erentialgleichungen im komplexen[J].Ann. Polon.Math.,1980,38:259-287.
[13]Gao Lingyun,Zhang Yu,Li Haichou.Growth of solutions of complex non-linear algebraic dif f erential equations[J].J.Math.,2011,31(5):785-790.
[14]Liao Liangwen,Yang Chungchun.On the growth of meromorphic and entire solutions of algebraic dif f erential equations[J].Ann.Mat.Pura Appl.,2001,IV(CLXXIV):149-158.
[15]Zalcman L.Normal families:new perspectives[J].Bull.Amer.Math.Soc.,1998,35:215-230.
[16]Yuan Wenjun,Xiao Bing,Zhang Jianjun.The general result of Gol’dberg’s theorem concerning the growth of meromorphic solutions of algebraic dif f erential equations[J].Compu.Math.Appl.,2009, 58:1788-1791.
[17]Clunie J,Hayman W K.The spherical derivative of integral and meromorphic functions[J].Comment.Math.Helv.,1966,40(1):117-148.
二阶代数微分方程亚纯解的增长性估计
张建军1,袁文俊2
(1.江苏第二师范学院数学与信息技术学院,江苏南京210013)
(2.广州大学数学与信息科学学院,广东广州510006)
本文研究了代数微分方程亚纯解的增长级.运用正规族理论,给出了某类二阶代数微分方程亚纯解的增长级的一个估计,该估计依赖于方程的有理函数系数.推广了2001年廖良文与杨重骏的一个结果.
代数微分方程;亚纯解;增长级
O174.5
A
0255-7797(2017)05-0925-07
∗Received date:2016-08-19Accepted date:2016-08-31
Supported by Natural Science Foundation of Jiangsu Province(BK20140767); Natural Science Foundation of the Jiangsu Higher Education Institutions(14KJB110004);Qing Lan Project of Jiangsu Province.
Biography:Zhang Jianjun(1982-),male,born at Taixing,Jiangsu,associate professor,major in complex analysis.
2010 MR Subject Classif i cation:34A34;30D35
