COMPLETE CONVERGENCE FOR ARRAYS OF ROWWISE M-NSD RANDOM VARIABLES
2017-09-15FENGFengxiangWANGDingchengWUQunying
FENG Feng-xiang,WANG Ding-cheng,WU Qun-ying
(1.School of Mathematical Science,University of Electronic Science and Technology of China, Chengdu 611731,China)
(2.College of Science,Guilin University of Technology,Guilin 541004,China)
COMPLETE CONVERGENCE FOR ARRAYS OF ROWWISE M-NSD RANDOM VARIABLES
FENG Feng-xiang1,2,WANG Ding-cheng1,WU Qun-ying2
(1.School of Mathematical Science,University of Electronic Science and Technology of China, Chengdu 611731,China)
(2.College of Science,Guilin University of Technology,Guilin 541004,China)
In this article,we study complete convergence theorems for arrays of rowwise m-negatively superadditive-dependent(m-NSD)random variables.By using Kolmogorov-type exponential inequality for m-NSD random variables,we obtain complete convergence theorems for arrays of rowwise m-NSD random variables,which generalize those on complete convergence theorem previously obtained by Hu et al.(1998)and Sung et al.(2005)from independent distributed case to m-NSD arrays.Our results also extend the corresponding results of Chen et al.(2008),Hu et al.(2009),Qiu et al.(2011)and Wang et al.(2014).
Kolmogorov-type exponential inequality;complete convergence;m-NSD random variables
1 Introduction
We f i rst introduce some concepts of dependent random variables.The concept of negatively associated(abbreviated to NA in the following)random variables was introduced by Joag-Dev and Proschan[1].
Def i nition 1.1A f i nite family of random variables{Xi;1≤i≤n}is said to be NA if for every pair of disjoint subsets A,B⊂{1,2,···,n},

whenever f and g are coordinatewise nondecreasing functions such that this covariance exists. An inf i nite family of random variables is NA if every f i nite subfamily is NA.
Def i nition 1.2(see[2])A function φ:Rn→R is called superadditive if φ(x∨y)+ φ(x∧y)≥φ(x)+φ(y)for all x,y∈Rn,where∨is for componentwise maximum and∧is for componentwise minimum.
The concept of negatively superadditive-dependent(abbreviated to NSD in the following)random variables was introduced by Hu[3]as follows.
Def i nition 1.3A random vector X=(X1,X2,···,Xn)is said to be NSD if

Hu[3]gave an example illustrating that NSD does not imply NA.Christof i des and Vaggelatou[4]indicated that NA implies NSD.
Hu et al.[5]introduced the concept of m-negatively associated random variables as follows.
Def i nition 1.4 Let m≥1 be a f i xed integer.A sequence of random variables{Xn;n≥1}is said to be m-negatively associated(abbreviated to m-NA in the following)if for any n≥2 and i1,···,insuch thatm for all 1≤k 6=j≤n,we have that Xi1,···,Xinare NA.
The concept of m-NA random variables is a natural extension from NA random variables (wherein m=1).
Similarly,we can def i ne m-NSD random variables.
Def i nition 1.5Let m≥1 be a f i xed integer.A sequence of random variables {Xn;n≥1}is said to be m-negatively superadditive-dependent(abbreviated to m-NSD in the following)if for any n≥2 and i1,···,insuch that|ik-ij|≥m for all 1≤k 6=j≤n, we have that(Xi1,···,Xin)is NSD.
Hsu and Robbins[6]introduced the concept of complete convergence of a sequence of random variables.Hu et al.[7]proposed the following general complete convergence of rowwise independent arrays of random variables.
Theorem ALet{Xni;1≤i≤kn,n≥1}be an array of rowwise independent random variables and{cn}be a sequence of positive real numbers.Suppose that for every ε>0 and some δ>0,

The proof of Hu et al.[7]is mistakenly based on the fact that the assumptions of Theorem A imply convergence in probability of the corresponding partial sums.Hu and Volodin[8]and Hu et al.[9]presented counterexamples to this proof.They mentioned that whether Theorem A was true remained open.Since then many authors attempted to solve this problem.Hu et al.[9]and Kuczmaszewska[10]gave partial solution to this question. Sung et al.[11]completely solved this problem by using a symmetrization procedure and Kruglov et al.[12]obtained the complete convergence for maximum partial sums by using a submartingale approach.
Recently,Chen et al.[13]extended Theorem A to the case of arrays of rowwise NA random variables and obtained the complete convergence for maximum partial sums.Hu et al.[5]obtained complete convergence for maximum partial sums similar to Theorem A for arrays of rowwise m-NA random variables.Qiu et al.[14]obtained similar result for arrays of rowwise ND random variables.Wand et al.[15]extended and improved Theorem A for NSD arrays.Qiu[16]obtained similar result for weighted sums of NA random variables. The main purpose of this article is to generalize and improve Theorem A for the case of arrays of rowwise m-NSD random variables.
2 Main Results
Theorem 2.1Let{Xni;1≤i≤kn,n≥1}be an array of rowwise m-NSD random variables and{cn}be a sequence of positive real numbers.Assume that for every ε>0 and some δ>0,
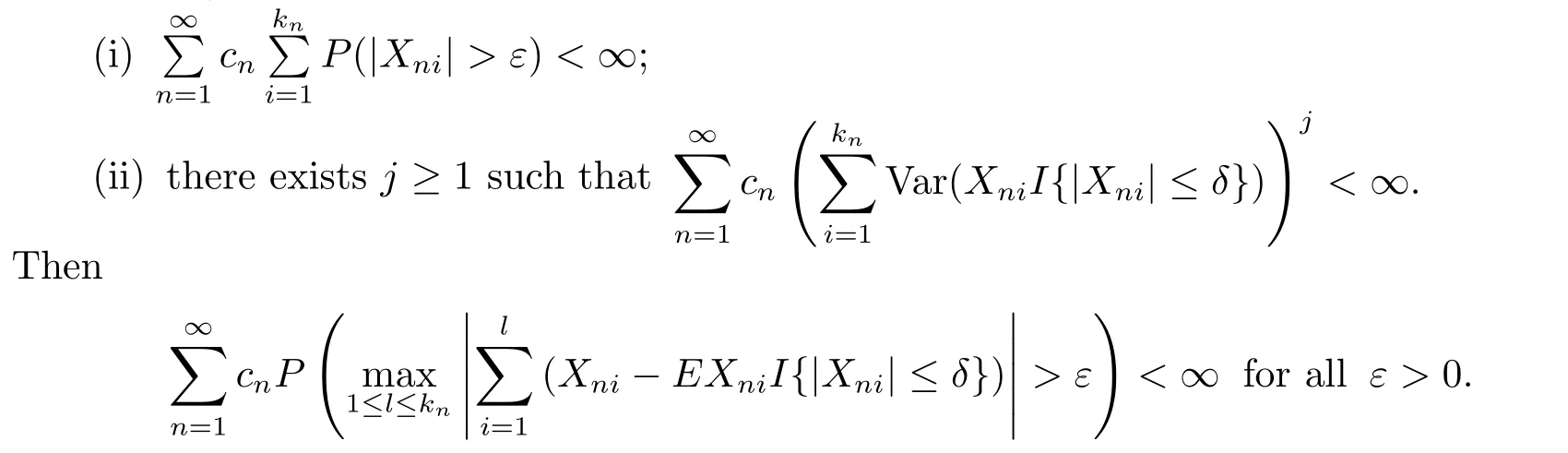
From Theorem 2.1,we can obviously obtain the following corollary.
Corollary 2.1Let{Xni;1≤i≤kn,n≥1}be an array of rowwise m-NSD random variables.If conditions(i)and(ii)of Theorem 2.1 and
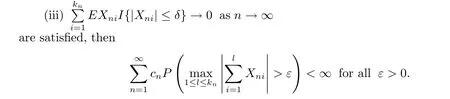
Theorem 2.2Let{Xni;1≤i≤kn,n≥1}be an array of rowwise m-NSD random variables with EXni=0 and EX2ni<∞for 1≤i≤kn,n≥1.Let{cn}be a sequence of positive real numbers.Assume that for every ε>0 and some δ>0,

Remark 1Corollary 2.1 shows that the main results of Hu et al.[7]and Sung et al. [11]remain true for m-NSD random variables.We generalize the corresponding complete convergence theorems from the independent case to m-NSD arrays without adding any extra conditions.
Remark 2In Theorem 2.2,we only need conditions(i)and(ii)of Corollary 2.1. Condition(iii)of Corollary 2.1 is not needed.Therefore Theorem 2.2 extends and improves the corresponding results of Hu et al.[7]and Sung et al.[11].In addition,our results also extend the corresponding results of Chen et al.[13],Hu et al.[5],Qiu et al.[14]and Wang et al.[15].When m=1,from Theorem 2.1 and Theorem 2.2,we can obtain the results of Theorem 3.3 and Theorem 3.2 of Wand et al.[15],respectively.We mention that Theorem 2.1 of this paper not only extends the results of Wand et al.[15]but also we have a simpler proof.More precisely,we only divide the sum into two parts in our proof instead of into four parts as was in the paper of Wand et al.[15].
Throughout this paper,C denotes a positive constant which may dif f er from one place to another.
3 Proofs of Main Results
In order to prove our results,we need the following lemmas.
Lemma 3.1(cf.Wand et al.[15],Lemma 2.4)Let{Xn;n≥1}be a sequence of NSD random variables with EXn=0 and EX2n<∞,n≥1.Let

Then for all x>0,a>0,
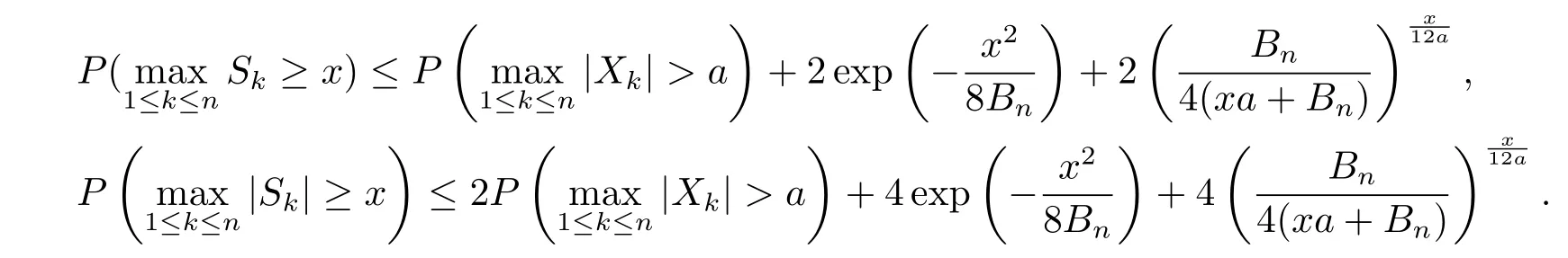
Lemma 3.2 Let{Xn;n≥1}be a sequence of m-NSD random variables with EXn=0 and EX2n<∞,n≥1.LetTherefore by Lemma 3.2,the conclusion holds.


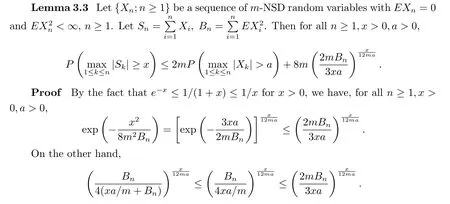
Proof of Theorem 2.1Let Yni=δI{Xni>δ}+XniI{|Xni|≤δ}-δI{Xni<-δ} and Y′ni=δI{Xni>δ}-δI{Xni<-δ}and 1≤i≤kn,n≥1.{Yni,1≤i≤kn,n≥1} is an array of rowwise m-NSD random variables.Note that



[1]Joag-Dev K,Proschan F.Negative association of random variables with applications[J].Ann.Stat., 1983,11:286-295.
[2]Kemperman J H B.On the FKG-inequalities for measures on a partially ordered space[J].Proc. Akad.Wetenschappen,Ser.A.,1997,80:313-331.
[3]Hu T Z.Negatively superadditive dependence of random variables with applications[J].Chinese J. Appl.Prob.Stat.,2000,16:133-144.
[4]Christof i des T C,Vaggelatou E.A connection between supermodular ordering and positive/negative association[J].J.Multi.Anal.,2004,88:138-151.
[5]Hu T C,Chiang C Y,Taylor R L.On complete convergence for arrays of rowwise m-negatively associated random variables[J].Nonl.Anal.,2009,71:1075-1081.
[6]Hsu P,Robbins H.Complete convergence and the law of large numbers[J].Proc.Natl.Acad.Sci. USA.,1947,33:25-31.
[7]Hu T C,Szynal D,Volodin A.A note on complete convergence for arrays[J].Stat.Prob.Lett.,1998, 38:27-31.
[8]Hu T C,Volodin A.Addendum to“A note on complete convergence for arrays”[J].Stat.Prob. Lett.,2000,47:209-211.
[9]Hu T C,Ord´o˜nez Cabrera M,Sung S H,Volodin A.Complete convergence for arrays of rowwise independent random variables[J].Commun.Korean Math.Soc.,2003,18:375-383.
[10]Kuczmaszewska A.On some conditions for complete convergence for arrays[J].Stat.Prob.Lett., 2004,66:399-405.
[11]Sung S H,Hu T C,Volodin A I.More on complete convergence for arrays[J].Stat.Prob.Lett., 2005,71:303-311.
[12]Kruglov V M,Volodin A I,Hu T C.On complete convergence for arrays[J].Stat.Prob.Lett.,2006, 76:1631-1640.
[13]Chen PY,Hu T C,Liu X,Volodin A.On complete convergence for arrays of row-wise negatively associated random variables[J].The.Prob.Appl.,2008,52(2):323-328.
[14]Qiu Dehua,Chang Kuangchao,Antonini R G,Volodin A.On the strong rates of convergence for arrays of rowwise negatively dependent random variables[J].Stoch.Anal.Appl.,2011,29:375-385.
[15]Wang Xuejun,Deng Xin,Zheng Lulu,Hu Shuhe.Complete convergence for arrays of rowwise negatively superadditive-dependent random variables and its applications[J].Stat.J.Theo.Appl. Stat.,2014,48(4):834-850.
[16]Qiu Dehua.Complete convergence for arrays of rowwise NA random variables[J].J.Math.,2013, 33(1):138-146.
行m-NSD随机变量阵列的完全收敛性
冯凤香1,2,王定成1,吴群英2
(1.电子科技大学数学科学学院,四川成都611731)
(2.桂林理工大学理学院,广西桂林541004)
本文研究了行m-NSD随机变量阵列的完全收敛性问题.主要利用m-NSD随机变量的Kolmogorov型指数不等式,获得了行m-NSD随机变量阵列的完全收敛性定理,将Hu等(1998)and Sung等(2005)的结果从独立情形推广到了m-NSD随机变量阵列.本文的结论同样推广了Chen等(2008), Hu等(2009),Qiu等(2011)和Wang等(2014)的结果.
Kolmogorov型指数不等式;完全收敛性;m-NSD随机变量
O211.4
A
0255-7797(2017)05-0889-09
∗Received date:2015-08-11Accepted date:2016-04-08
Supported by National Natural Science Foundation of China(71271042; 11361019);Research Project of Guangxi High Institution(YB2014150).
Biography:Feng Fengxiang(1975-),female,born at Guilin,Guangxi,associate professor,major in probability and statistics.
2010 MR Subject Classif i cation:60F15;60E05
猜你喜欢
———理学院
