图书销售点选址问题的多种解法

孙 峰

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

图书销售点选址问题的多种解法

孙 峰

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

文章对具体的数学建模问题—图书销售代理点的选址问题作了详细讨论。借助图论知识，从选边和选点的角度出发，给出了该问题的多种解法。此外，对该选址问题作了推广，并给出了相应的解法。

数学建模；选址问题；多种解法；图论

数学是各门自然科学、工程科学乃至社会科学的基础，在人类历史发展和社会生活中发挥着不可替代的作用，也是学习和研究现代科学技术必不可少的基本工具。数学的应用领域十分广泛，数学的重要性得到大家的广泛认同。然而，作为一门基础的自然学科和一种精确的科学语言，数学又是以极为抽象的形式出现的。如果人为地割断数学与现实世界的密切联系，这种抽象的形式就会掩盖数学的丰富内涵，并对数学的实际应用造成巨大障碍。数学建模可以说是解决这个问题的一把钥匙，它在实际问题与数学之间架设了一座桥梁，为实际问题的解决提供了强有力的工具[1]。数学建模是一种运用数学的语言和方法，通过抽象、简化建立起的能近似刻画并“解决”实际问题的一种强有力的数学手段。对于建模问题而言，不同的假设建立不同的模型，不同的分析角度往往会得到不同的解决办法。从不同的角度分析看待问题，不仅能加深对问题的理解，而且有助于拓宽知识面、提高创新能力。图书销售代理点的选址问题是经典数学建模教材中的一个习题[2]，本文就这一问题，从不同角度出发，分析解决该问题。

1 图书销售代理点选址问题

一家出版社准备在某市建立两个销售点，向7个区的大学生售书，每个区的大学生数量（单位：千人）已经表示在图1上。每个销售代理点只能向本区和一个相邻区的大学生售书，这两个代理点应该建在何处，才能使所能供应的大学生的数量最大？

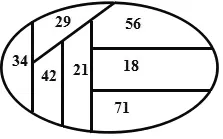
图1 各区情况

2 图书销售代理点选址问题的分析与假设

该问题要求我们选择图书销售区域使得所能供应的学生数达到最大。这是一个典型的数学规划问题，建立数学规划模型的关键在于理清决策、目标和约束。该问题的决策是图书销售区的选择，目标是使得所能供应的学生数最大，也即是图书销售区的学生数量总和最大，约束是所选择的销售代理点只能向本区和一个相邻区的大学生售书。

对于区域的相邻关系，我们可以借助图论的知识，将区与区之间的相邻关系用图表示（见图2，图论有关知识可参见文献[3]），其中图2中的7个点分别代表7个区，点与点之间存在一条边当且仅当这两点所代表的区相邻。

对于这一问题，我们可以将决策视为选择2个代理点并确定各代理点相应的售书区，即从图2中的7个顶点选取2个，然后再选择与所选顶点有边相连的另外2个顶点；也可以将决策视为选择4个销售区，即从图2中的7个顶点选取4个。当决策变量选定后，再根据决策变量给出相应的目标函数和约束即可得到该问题的数学规划模型。

通过对该问题的分析，我们提出以下假设：

1）每个销售代理点只能向本区和一个相邻区的大学生售书；

2）售书所面向的人群仅考虑为大学生，且售书的多少与售书区的大学生数成正比；

3）不考虑各区之间的学生流动；

4）为使供应人数最大，不存在重复供应的情况，即每一个区至多只有一个代理点供应。

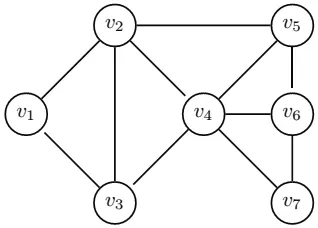
图2 各区相邻情况关系

3 图书销售代理点选址问题的模型建立及求解

基于上一节的分析，我们可以从不同角度入手：选择2个代理点并确定各代理点相应的售书区，即从图2中的7个顶点选取2个，然后再确定与所选顶点有边相连的另外2个顶点（将该方法简记为“7选2”），这也相当于从图2的11条边中选取2条（将该方法简记为“11选2”）；或者选择4个销售区（将该方法简记为“7选4”）。下面我们针对不同的角度，给出该问题相应的解法。

3.1 解法一：“11选 2”

当一个销售代理点确定在某个区时，我们还需要确定向哪一相邻区域售书，这相当于选中相邻的两个区，也即是图2中的一条边，因此该选址问题等价于从图2的11条边中选取2条边使得供应的人数达到最大。选取的2条边互不共用顶点，若共用顶点的话，图书实际供应的区域仅有3个，这无疑不能满足供应人数最大。

记ri为第i区大学生人数；用0-1变量xij（i＜j且vi，vj相邻）表示是否选中连接顶点vi与vj的边，若选中连接顶点vi与vj的边，即i，j两区有一个销售代理点供应图书，则 xij=1，否则xij=0。

于是我们可得到该选址问题的0-1规划模型：

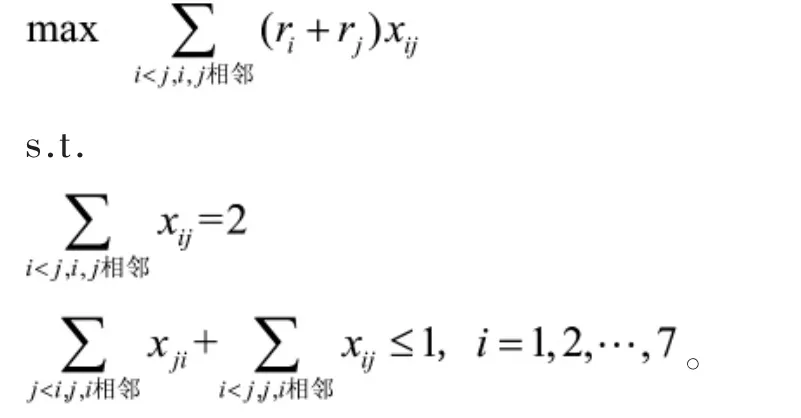
具体模型如下：

模型求解结果为x25=x47=1，即第2，5区及第4，7区之间有销售代理点，总供应人数是177千人。

3.2 解法二：“7选2”

从7个区中选2个建立销售代理点，并根据选择的代理点分别确定相邻的售书区。当区1选定时，为使供应人数最多，则向区3供应；区2选定，则向区5供应；区3选定，则向区1供应；区4选定，则向区7供应；区5选定，则向区2供应；区6选定，则向区7供应；区7选定，则向区4供应。记ri为第i区大学生人数，用0-1变量xi=1表示在第i区建立图书销售代理点，否则xi=0。

所能供应的学生人数为：

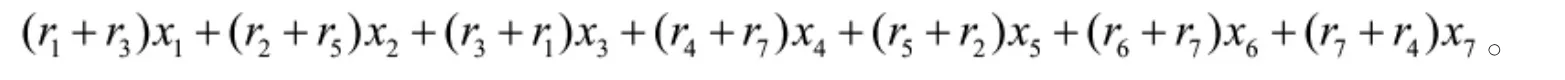
区1选定则向区3供应，反过来，区3选定则向区1供应，即是说选区1与选区3等价，因此区1与区3中至多选一个：x1+x3≤1。

选区2与选区5等价，因此区2与区5中至多选一个：x2+x5≤1。

选区6则选区7，选区7与选区4等价，因此区4、区6、区7中最多选一个：x4+x6+x7≤1。

从而我们得到下述模型：

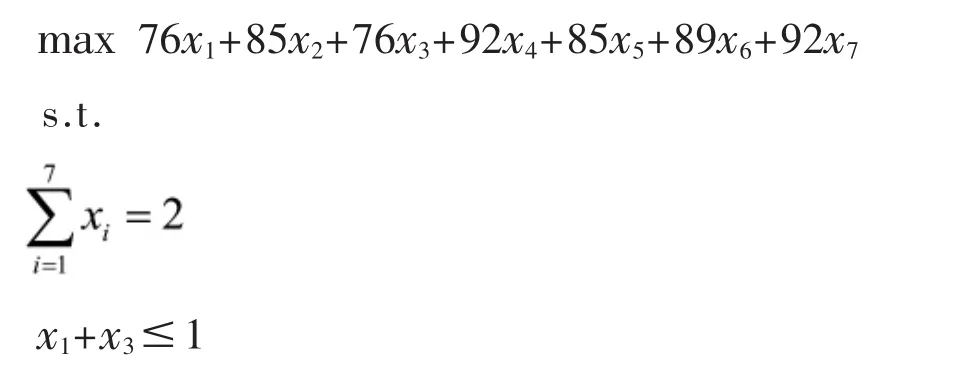
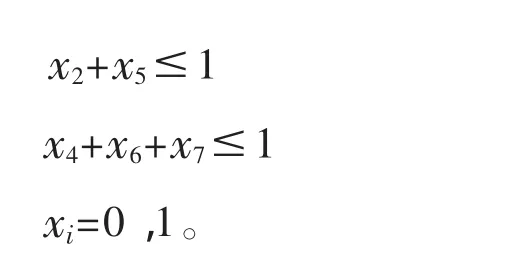
模型求解结果为 x2＝x4＝1，即第2，5区及第4，7区之间有销售代理点，总供应人数177千人。

3.3 解法三：“7选4”细分法

从7个区中选2个建立销售代理点，并分别向相邻的某个区供应。这相当于从7个区中选取4个，不过所选取的4个区能分为两组，两个区一组且同一组中的两个区相邻。对于同一组中的两个区相邻的约束条件，我们可以细分为相邻两区的固定搭配：当区1选定时，为使供应人数最多，则向区3供应；区2选定，则向区5供应；区3选定，则向区1供应；区4选定，则向区7供应；区5选定，则向区2供应；区6选定，则向区7供应；区7选定，则向区4供应。记ri为第i区大学生人数；用0-1变量xi=1表示在第i区建立图书销售代理点，否则xi=0。

同一组中的两个区相邻可细分为如下情形：

选区 1 必选区 3，选区 3 必选区 1：x1＝x3。

选区 2 必选区 5，选区 5 必选区 2：x2＝x5。

选区 4 必选区 7，选区 7 必选区 4：x4＝x7。

选区 6 必选区 7：x7≥x6。

综上，我们得到如下模型：

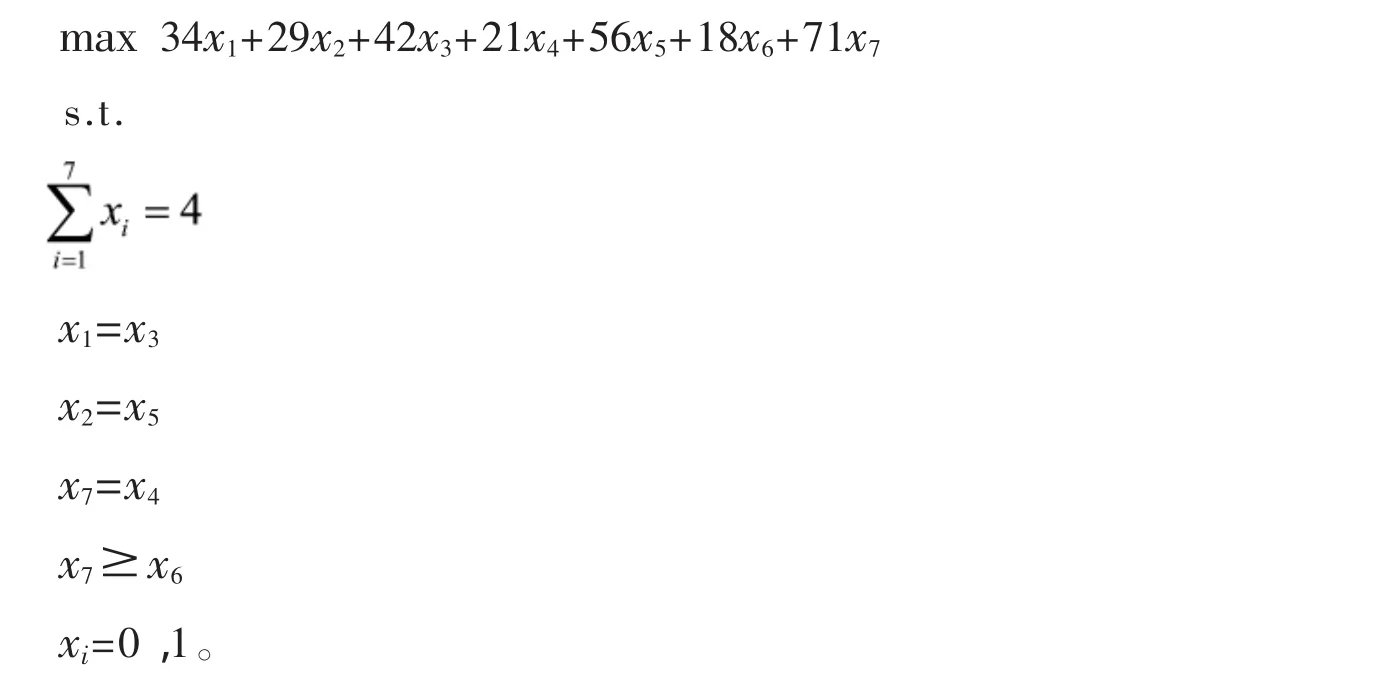
模型求解结果为 x2=x4=x5=x7=1，即第2，5区及第4，7区之间有销售代理点，总供应人数177千人。

3.4 解法四：“7选4”矩阵法

从7个区中选取4个，使得所选取的4个区能分为两组，两个区一组且同一组中的两个区相邻，这相当于从邻接矩阵的主对角线的上方选取2个位于不同行不同列的1，这两个1所在的行和列就是我们要选择的4个区。

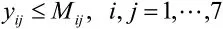
y 与 x 的关系：yij≤xi，yij≤xj。

综上，我们得到下述模型：

模型求解结果为 y25=y47=1，x2=x4=x5=x7=1，即第2，5区及第4，7区之间有销售代理点，总供应人数177千人。

4 问题推广

在上一节，我们考虑了从7个区选取2个销售代理点的选址问题，我们将区之间的相邻关系以图的形式表示，或从选点或从选边的方面考虑该问题，给出了该问题的不同解法。现在我们讨论更一般的情况：从n个区选取m（n＞2m）个销售代理点的选址问题，同样要求每个销售代理点只能向本区和一个相邻区售书。

基于上一节的讨论，我们在此给出该推广问题的几种解决办法。首先将各区的相邻关系表示为图 G=（V，E），其中 V={v1，v2，…，vn}为顶点集表示 n个区；E为边的集合，表示各区的相邻情况，若区i与区j相邻，则边（vi，vj）∈E，否则（vi，vj）E。令图G=（V，E）的邻接矩阵为M，其中Mij=1当且仅当（vi，vj）∈E，Mij=0当且仅当（vi，vj）E。记={1，2，…，n}，ri为区i大学生数，（表示与区 i相邻的所有区，表示与区i相邻的区中学生数达到最大的区，表示的最小元，即与区i相邻的区中学生数达到最大的区中编号最小的区。

4.1 基于选边的解决办法

设xij为0-1变量，表示i，j两区间是否建立销售代理点，若在i，j两区间建立销售代理点，则xij=1，否则 xij=0。

于是我们得到供应人数最大化的选址模型：

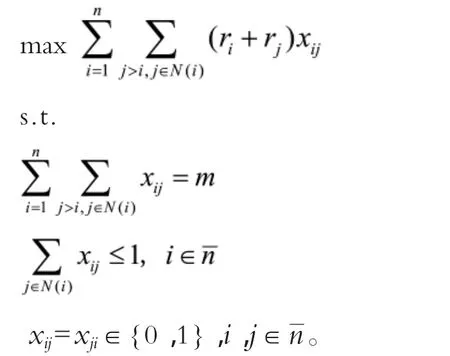
4.2 基于选点的解决办法

设xi为0-1变量，表示是否向i区售书，如果是，则 xi=1；否则 xi=0。从n个区选取 m个建立销售代理点，并向相邻的某个区供应。这相当于从n个区选取2m个区售书。若向i区售书，则必然在N(i)中的某区售书，更进一步，为使供应人数达到最大，必然向中的某区售书。当然，由的定义可知向i中的任意一区售书都可以，在这里不妨设其为。即当xi=1时，必然有，因而有。

于是得到供应人数最大化的选址模型：

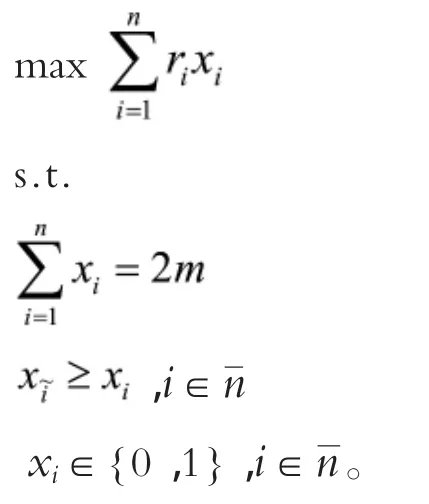
4.3 基于选边与选点结合的解决办法

边与点的关系，即若i，j两区存在销售代理点，则必然选i，j两区：。

综上，相应的模型如下：

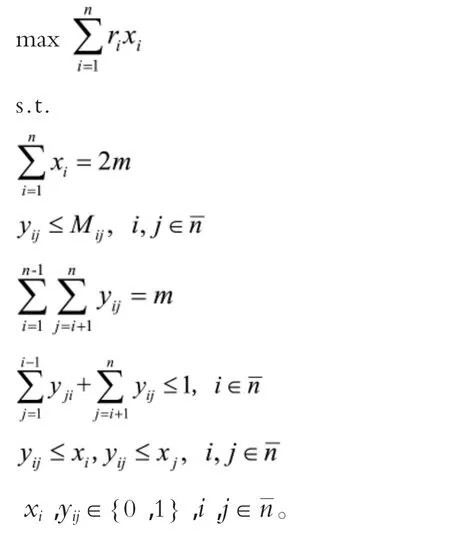
5 小结

对于图书销售代理点的选址问题，我们将区之间的相邻关系，以图（7个顶点，11条边）的形式表示，或从选点或从选边的方面考虑该问题，给出了该具体问题的4种不同解法，并进一步给出了这类问题的通用模型及其求解。

参考文献：

[1]姜启源，谢金星.一项成功的高等教育改革实践：数学建模教学与竞赛活动的探索与实践[J].中国高教研究，2011（12）：79-83.

[2]姜启源，谢金星，叶俊.数学模型[M].4版.北京：高等教育出版社，2011.

[3]DIESTEL R.Graph theory[M].4th ed.Springer，2010.

Multiple Solutions to Location Selection Issue of Book Sales

SUN Fenɡ
（School of Mathematics and Information Science，Leshan Normal University，Leshan Sichuan 614000，China）

The specific mathematical modeling issue which means the location selection issue of book sales has been discussed in details in this paper.Based on graph theories，this paper also gives multiple methods to solve the location selection issue within the viewpoints of choosing edges or vertices.In addition，the location problem has been generalized and the corresponding solution has been given as well.

Mathematical Modeling；Location Selection Problem；Multiple Solutions；Graph Theory

O29

A

1009-8666（2017）08-0038-08

［责任编辑、校对：方忠］

10.16069/j.cnki.51-1610/g4.2017.08.008

2016-05-25

四川省省级精品资源共享课建设项目“数学建模与数学实验”（2013-123）

孙峰（1985—），男，四川西昌人。乐山师范学院副教授，博士，研究方向：不确定性的数学理论、数学建模等。