允许k次幂等和对角化的符号模式矩阵

冯新磊

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

允许k次幂等和对角化的符号模式矩阵

冯新磊

（乐山师范学院 数学与信息科学学院，四川 乐山 614000）

刻画符号模式矩阵的允许对角化一直是一个著名的开问题。文章给出了一个符号k次幂等符号矩阵允许k次幂等的充要条件，同时，也获得了一个符号k次幂等符号模式矩阵允许k次幂等也允许对角化的结论。

符号模式；允许对角化；符号k次幂等；允许k次幂等

1 引言和初步知识

符号模式（矩阵）的产生是源于解决经济和其他领域的某些问题，仅仅需要矩阵的元素的正负性，不涉及元素的大小，它已经被广泛地应用和研究[1-3]。特别地，特征值问题无论在传统矩阵还是在符号模式理论中都占有重要的地位[3-4]。寻找符号模式允许对角化的充要条件一直是一个至今没有彻底解决的问题。关于这个问题，Eschenbach和Johnson[2]，Shao和Gao[5]以及 Feng and Li etc[6]都给出了相关的结论。

Lee和 Jin[7]考虑了符号幂等符号矩阵允许幂等的问题。由此，我们打算进一步考虑符号k次幂等符号矩阵允许k次幂等的问题。另外，我们容易获得一个符号矩阵允许k次幂等也会允许对角化的结论。

下面我们介绍一些定义和概念，其中大部分能够在文献[2-3][5]中找到。

一个符号模式是元素仅仅由{+，-，0}构成的矩阵，所有n×n的符号模式矩阵记成n。对于 A=[aij]∈n，是一类元素符号相同的实矩阵的集合，记成(A)={B=[bij]∈Mn(R)｜sgn bij=aij}，对所有 i和 j}，B∈(A)是指 sgn(B)=A。

一个广义符号模式[4]是指元素由{+，-，0，#}构成的矩阵，这里#表示一个模糊数(+与-相加的结果)。一个符号模式的乘积可能是一个广义符号模式。在本文中，我们主要考虑符号模式矩阵。一个符号矩阵A叫做可幂的，是指A1，A2，A3，…，都是符号模式矩阵。

对于一个符号模式A，令P是关于一个实矩阵的性质，如果存在一个实矩阵B∈(A)有性质P，我们说A允许P。

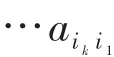
一个n×n符号矩阵A=[aij]的符号有向图记成D(A)，是指由节点集{1，2，…，n}构成的有向图，其中(i，j)是一条弧当且仅当 aij≠0。令 A=[aij]是一个 n×n符号模式，一个形式为的非零乘积，叫做一个长度为k的简单环，这里下标i1，…ik互不相同，每个im(m=1，…，k)叫做γ的一个节点，总长度为k的下标集互不相同的简单环的乘积叫做一个长度为k的组合环。A的最大的组合环的长度记成c(A)。如果A简单环都没有，则c(A)=0。

类似地，定义 A的最小秩A，mr(A)，为mr(A)=min{秩B｜B∈(A)}。

一个置换符号矩阵是指元素为0和 +的方阵，且元素+在矩阵的每行每列只能且必须出现一次。容易得到置换符号矩阵P∈n满足方程PTP=PPT=In，其中In是n阶单位符号模式矩阵，也即它是主对角元素都是+的对角符号模式。

两个符号模式 A1，A2∈n是置换相似的，是指存在置换符号矩阵P使得A2=PTA1P成立。

下面给出两个将要用到的引理。

引理1.1[5]令A∈n，如果在A中存在某个长度为k的无弦组合环，那么A允许对角化，其中 mr(A)≤k≤mR(A)。

引理1.2[6]一个符号模式A∈n允许对角化当且仅当存在一个秩为k的实矩阵B∈(A)，其有一个非奇异的k×k的主子矩阵。

本文内容安排如下：在第二部分我们考虑了符号幂等符号矩阵允许对角化的问题；第三部分，我们获得了符号k次幂等符号矩阵允许k次幂等的充要条件，同时，也给出了符号k次幂等符号模式矩阵允许k次幂等也允许对角化的结论。

2 符号幂等符号矩阵

在本文中，允许对角化是我们重点关注的问题。Lee和 Jin[7]获得了符号幂等符号矩阵允许幂等的一些结论，在此基础上，我们容易发现符号模式允许幂等和允许对角化之间的关系。

对于可约的符号幂等符号矩阵记为PPO，是指如果Aii和Ajj的每个元素都是正的，则Aij=0。

引理2.1[7]令A是一个Frobenius标准形的可约的符号幂等符号模式，则A允许幂等当且仅当A是PPO。

因此我们能得到下面的结论。

定理2.2 令A是一个Frobenius标准形的可约的符号幂等符号模式，并且A是PPO的，那么A允许对角化。

3 允许k次幂等和对角化的符号k次幂等符号矩阵

通过约当标准形，容易得到对于任意正整数m，一个非奇异实矩阵B是可对角化的当且仅当Bm是可对角化的。但是对于符号矩阵，这个结论是不成立的。如果A允许对角化，那么Am允许对角化；但是Am允许对角化，A可能不允许对角化。基于此，在这部分，我们想弄清楚上面提到的关系，同时，我们也仅考虑符号模式是可幂的情况。

引理 3.1[8]令A是一个不可约的符号k次幂等符号模式，其有块m×m环模式，m≥1。对于1≤i≤m，令Ji表示元素都是+的与Ai型号一样的矩阵；并且令Ci表示Ai的第一列，那么，当m∈{k/2，k}，1≤i≤m，存在向量 ui属于{+Ci，-Ci}使得 Ai=uiui+1T；当 1≤i≤m-1(m≥2)，那么 Am=αumu1T，其中α=+，当m=k时，α=-，当m=k/2时，进一步，如果 D=diag(u1，u2，…，um)，那么

由上面引理 3.1，我们能得到下面的结论。

定理3.1 如果A是一个不可约符号k次幂等符号矩阵，那么A允许k次幂等。

证明 如果A是一个不可约符号k次幂等符号矩阵，且A的非本原指标为m，m≥2，那么存在置换矩阵P，通过置换相似使得A变成 Frobenius标准形，记为PTAP=。由引理3.1，∃D，使得相似于

类似于定理2.1，A允许k次幂等，明显地，A也允许对角化。因此，我们有：

推论 3.1 如果A是一个不可约符号k次幂等符号矩阵，那么A也允许对角化。

下面的部分我们将考虑可约符号k次幂等符号矩阵。

定理3.2 如果A是一个可约的主对角线上无零元素的Frobenius标准形的符号k次幂等符号矩阵，那么A允许k次幂等当且仅当A是不可约符号k次幂等符号矩阵的直和。

证明 如果A是一个可约的主对角线上无零元素的Frobenius标准形的符号k次幂等符号矩阵，那么

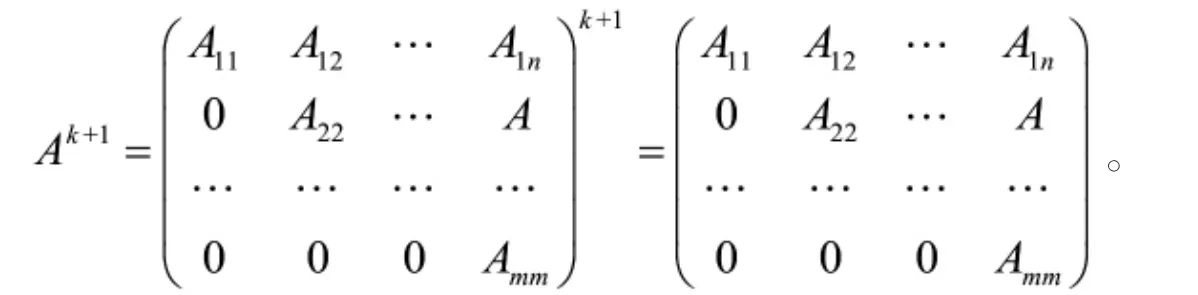
根据矩阵的乘法，我们可以得到

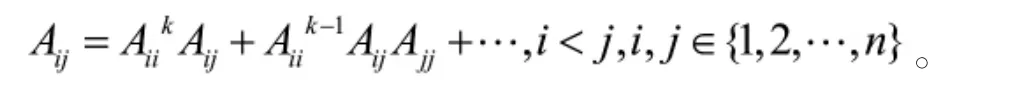
上面方程的两边同时左乘Aii，我们得到

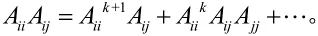
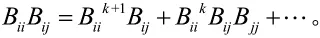
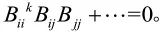
AiiAij是不模糊的，因此上面方程左边的每一项应该为0，即，。因此，我们能得到另外，因为Aii和Aij是不可约符号k次幂等符号矩阵，我们能够得到

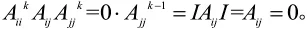
所以结论成立。

定理3.3 如果A是一个可约的Frobenius标准形的符号k次幂等符号矩阵，那么A允许k次幂等当且仅当A是不可约符号k次幂等符号模式的直和，或者在主对角块上存在一些零块，其他的是不可约符号k次幂等符号模式矩阵。

证明 根据定理3.2，我们仅需要证明在主对角块上存在零块的情况就行了。令

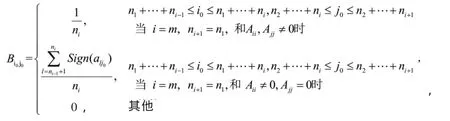
推论 3.2 如果A是一个可约的符号k次幂等符号矩阵且允许k次幂等，那么A允许对角化。

在这部分我们仅考虑了符号k次幂等符号矩阵允许k次幂等，那么它也允许对角化的情况。以后A允许对角化和Am的允许对角化的关系仍值得进一步研究。

[1]BRUALDI R A，SHADER B L.Matrices of sign-solvable linear systems[M].Cambridge：Cambridge University Press，1995：1-316.

[2]ESCHENBACH C A，JOHNSON C R.Sign patternsthat require repeated eigenvalues[J].Linear Algebra and its Applications，1993（190）：169–179.

[3]HALL F，LI Z S.Sign pattern matrices[M]//Handbook of Linear Algebra，Chap.33，L.Hogben，ed.，Boca Raton：Simon and Hall/CRC Press，2007：1-20.

[4]HORN R A，LOPATIN A K.The moment and Gram matrices，distinct eigenvalues and zeroes，and rational criteria for diagonalizability[J].Linear Algebra and its Applications，1999（299）：153–163.

[5]SHAO Y，GAO Y.Sign patterns that allow diagonalizability[J].Linear Algebra and its Applications，2003，（359）：113–119.

[6]FENGXL，HUANG T Z，LI Z S，et al.Sign patterns that allow diagonalizability revisited[J].Linear and Multilinear Algebra，2013，（61）：1223–1233.

[7]LEE S G，PERK J W.Sign idempotent sign pattern matrices that allow idempotence[J].Linear Algebra and its Applications，2015（487）：232–241.

[8]STUART J，ESCHENBACH C，KIRKLAND S.Irreduciblesign k-potent sign pattern matrices[J].Linear Algebra and its Applications，1999（294）：85-92.

Matrix of Coincidence Mode with Acceptable K-power of Similarity and Diagonalization

FENG Xinlei
（School of Mathematics and Information Science，Leshan Normal University，Leshan Sichuan 614000，China）

The acceptable diagonalization of mat rix in symbolic pattern has always been a wellknown open problem.In this paper，the matrix of K-power symbolic pattern which accepts the necessary and sufficient condition for symbols like K-power is offered.Meanwhile，the result that a sign K-power symbolic pattern matrix accepts both k-powers and diagonalizability is obtained.

Symbolic Pattern；Acceptable Diagonalization；Sign K-power；Acceptable K-power

O157

A

1009-8666（2017）08-0001-05

［责任编辑、校对：李书华］

10.16069/j.cnki.51-1610/g4.2017.08.001

2017-05-02

四川省教育厅重点项目“多智能体系统一致性的最快收敛研究”（16ZA0304）

冯新磊（1979—)，男，山东聊城人。乐山师范学院数学与信息科学学院副教授，理学博士，研究方向：符号模式矩阵以及多智能体系统一致性。