湖南栎类天然混交林优势木树高曲线哑变量模型研究

2017-09-15朱光玉罗小浪

林业资源管理 2017年4期

关键词：混交林胸径样地

朱光玉,罗小浪

(中南林业科技大学,长沙 410004)

湖南栎类天然混交林优势木树高曲线哑变量模型研究

朱光玉,罗小浪

(中南林业科技大学,长沙 410004)

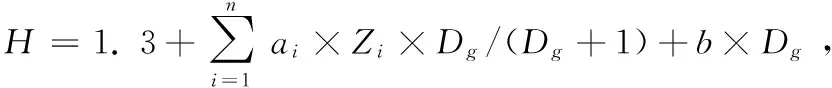
栎类混交林；优势木；树高曲线模型；哑变量

树高和胸径是森林资源调查中2个重要的林分测树因子[1],其中胸径在立木条件下容易测定,而树高由于受林分状况、立地条件和测定方法等因素的影响,使得测量较困难,且精度不高[2]。林业调查中往往采取抽样测定样地中一定比例不同径阶立木或全部立木的树高和胸径,通过建立树高直径模型来预测未知立木的树高[3]。到目前为止,树高-胸径关系仍然处于研究的前沿位置。

树高与胸径的关系常常受立地条件和树种结构的影响,不同树种间由于林分类型和立地类型的不同导致其树高-胸径关系通常存在较大的差异。因此,仅仅以胸径为自变量建立树高-胸径关系的简单模型不能有效反映不同林分类型和立地类型下树高、胸径生长的差异[4]。多年来,一般性树高曲线模型已经在林业生产和实践中广泛应用[5-10],但是几乎所有的研究都是针对人工林和天然纯林,而对天然混交林树高曲线模型的研究鲜有报道[11-13]。对于天然混交林,研究树高曲线模型时可以考虑增加林分类型和立地类型作为输入变量[14-15]。因此,研究建立基于哑变量的天然混交林优势木树高曲线模型,对探索栎类(QuercusL.)天然混交林的生长规律、立地质量评价和经营措施具有重要意义。

本文以湖南省栎类天然混交林为研究对象,样地数据来源于平江县芦头林场、桑植县八大公山、沅江市龙虎山、郴州市五盖山和宁乡县青羊湖林场。从目前研究应用较广的树高-胸径关系模型中选出精度较高的模型作为基础模型,再分别以林分类型和立地类型为哑变量建立湖南栎类天然混交林优势木树高曲线模型,为全国栎类混交林的研究和科学经营提供理论依据。

1 研究区概况

湖南省(24°38′～30°08′N,108°47′～114°15′E)地处中国中南部,长江中游,省会长沙,东西宽667km,南北长774km；地势东、西、南三面高,形成向东北面开口的马蹄形地貌。湖南为大陆性中亚热带季风湿润气候,全省年平均气温为16～18℃之间,年日照时数为1 300～1 800h,无霜期长达260～310d；年平均降水量在1 200～1 700mm之间,雨量充沛,为我国雨水较多的省区之一[16]。湖南土壤主要以红壤和黄壤为主,其次为紫色土和冲积土；红壤主要分布在洞庭湖平原及中东部的绝大部分地区,黄壤主要分布在湘西。

湖南栎类资源丰富,据统计有6属77种,呈现出分布不均匀、偏远、经纬度地带性差异和垂直地带性差异显著等特点[17]。其中常绿阔叶林主要有栲属(Castanopsis),石栎属(Lithocarpus),青冈属(Cyclobalanopsis),如湘中地带的苦槠(Castanopsissclerophylla)、枹栎(QuercusserrataThunb)和细叶青冈(Cyclobalanopsismyrsinaefolia(Blume)Oerst)等；落叶阔叶林主要有栎属(Quercus)、水青冈属(Fagus)和栗属(Castanea),如湘西和湘北地带的锥栗(Castaneahenryi(Skam) Rehd.et Wils)和亮叶水青冈(FaguslucidaRehd.et Wils)[18-19]。

2 研究方法

2.1 数据来源

数据来源于2015年12月—2016年8月,在湖南省平江县芦头林场、桑植县八大公山自然保护区、沅江市龙虎山森林公园、郴州市五盖山林场、宁乡县青羊湖林场5个地点共设置栎类天然混交林固定样地51块,对样地内胸径大于5cm的立木进行每木检尺,共调查立木3 888株。样地调查内容包括树高、胸径、年龄、冠幅等测树因子,海拔、坡度、坡位、坡向、土壤厚度、土壤类型等立地因子。模型建立数据如表1所示。

2.2 数据处理

2.2.1 优势木选择

优势木一直是研究中的一个重要指标[20],同一树种的优势木反映了不同的树高级。本研究选择优势木的方法有2种:一是选取样地内一株最高立木的树高,即最高优势木；二是根据样地优势树种组组成,在样地内选取3株位于优势树种组里的优势木(含亚优势木)树高,以其平均值作为优势木平均高,即平均优势木[21]。

表1 模型建立数据

2.2.2 林分类型哑变量

统计样地内各树种的胸高断面积,计算样地内各树种的组成系数(XSi)。

BA=ΣBAi

(1)

XSi=BAi/BA

(2)

BA为样地胸高断面积之和,BAi为样地内树种i的断面积,树种名称按照各树种组成系数从高到低排列[21]。为了划分优势树种组,定义XST=ΣXSi,取ΣXSi≥0.65时所包括的树种构成优势树种组。

根据优势树种组,基于样地5个不同的地点(芦头、八大公山、龙虎山、五盖山、青羊湖),本研究将51块样地划分为5种不同的林分类型(表2)。

表2 林分类型哑变量

2.2.3 立地类型哑变量

立地类型相比林分类型对林分的树高-胸径关系影响可能更显著,为探索这种显著性,本研究将初始立地类型聚类后作为哑变量进一步优化模型。根据立地因子(海拔、坡度、坡位、坡向、土壤类型、土壤厚度)的变化幅度及对立木优势木高生长发育的影响程度,采用R软件中k-means聚类,对各因子分级处理,聚类分析的分类数标准为聚类精度≥0.99。

2.3 基础模型选择

本研究中,选择应用最广泛的13种常见的树高-胸径关系模型[22-24](表3)作为研究栎类天然混交林优势木树高曲线的基础模型,探讨栎类混交林最优的树高曲线模型形式。

表3 树高-胸径关系基础模型

注:a,b,c为模型参数,H为优势木高(m),Dg为优势木胸径(cm)。

2.4 哑变量模型构建

哑变量,又称假变量或指示变量,基于哑变量的回归分析方法见李希非等[25]的方法。哑变量是对分类变量或定性因子进行处理的一种常用方法,统计分析中各种数量化方法都要涉及到哑变量处理的问题[26-28]；在各种回归分析和建模实践中也经常用到哑变量模型方法[29]。本文在构建通用性栎类混交林优势木树高曲线模型时,利用Forstat软件的非线性回归模块在保证预估精度的前提下尽量简化所建模型,分别建立含林分类型和立地类型哑变量的优势木树高曲线模型,选出最优模型形式。

基于模型1的哑变量模型的形式可表示为:

式中:Zi为哑变量,ai为相应的特定参数或局部参数。本研究中哑变量的处理包括2种情况:

1) 考虑林分类型:根据样地区域和优势树种组划分的林分类型,因为区域与树种并不独立,故相当于同时考虑了样地区域和树种,含5个哑变量(表2),Z1,Z2,Z3,Z4和Z5:

当林分类型为锥栗-甜槠混交林时,取Z1=1,Z2,Z3,Z4,Z5均为0；

当林分类型为亮叶水青冈混交林时,取Z2=1,Z1,Z3,Z4,Z5均为0；

依此类推。

2) 考虑立地类型:根据立地类型划分、聚类,最终分成几类就设定几个哑变量。假设分成了k类,则立地类型包含k个哑变量,Z1,Z2,Z3,…,Zk:

当立地类型属于Z1时,取Z1=1,Z2,Z3,…,Zk均为0；

当立地类型属于Z2时,取Z2=1,Z1,Z3,…,Zk均为0；

依此类推。

2.5 模型评价

模型检验采用确定系数(R2),AIC,均方根误差(RMSE)和预估精度(P)4个评价指标进行评价和比较,计算公式如下:

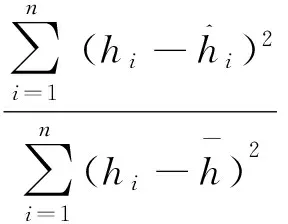
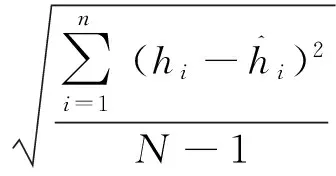
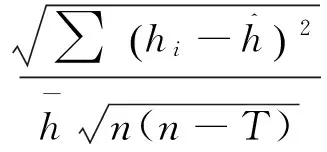
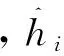
3 结果与分析

3.1 基础模型

基于样地平均优势木和最高优势木数据,采用各基础模型拟合的优势木树高曲线确定系数(R2)、均方根误差(RMSE)和预估精度(P)如表4所示。结果表明:平均优势木中模型M5确定系数(R2=0.376)和预估精度(P=95.31%)都是最大,均方根误差(RMSE=2.50)最小；最高优势木中同样是模型M5确定系数(R2=0.238)和预估精度(P=95.14%)都是最大,均方根误差(RMSE=22.98)最小。综合衡量2种优势木的拟合结果,平均优势木模型明显好于最高优势木模型,并选择模型M5作为构建含哑变量的优势木树高曲线模型的候选模型。

3.2 哑变量模型

3.2.1 林分类型哑变量拟合结果

以林分类型为哑变量加在候选模型M5不同参数(a,b,ab)上拟合,得出模型M5的各个评价指标值(表5),根据4个评价指标选出候选模型林分类型哑变量最优参数形式。

由表5可知,加入林分类型哑变量后,模型的拟合精度明显要优于未加哑变量的拟合:模型确定系数从0.376提高到0.711 9,且平均优势木拟合的确定系数大于最高优势木。两种优势木拟合中,哑变量加在模型M5参数a上比加在b上效果要好,哑变量同时加在参数a,b上时运行出现错误。对于平均优势木,哑变量加在模型M5参数a上的确定系数和预估精度最大,分别为0.711 9,96.91%,均方根误差和AIC最小,分别为1.64,209.64；对于最高优势木,同样是哑变量加在模型M5参数a上的确定系数和预估精度最大,分别为0.554 9,96.21%,均方根误差和AIC最小,分别为2.30,240.93。因此,综合评价指标得出:林分类型哑变量中2种优势木树高曲线模型以模型M5参数a上的拟合最佳,并进一步证实平均优势木模型要优于最高优势木模型。因此,立地类型哑变量模型中不再建立最高优势木模型。

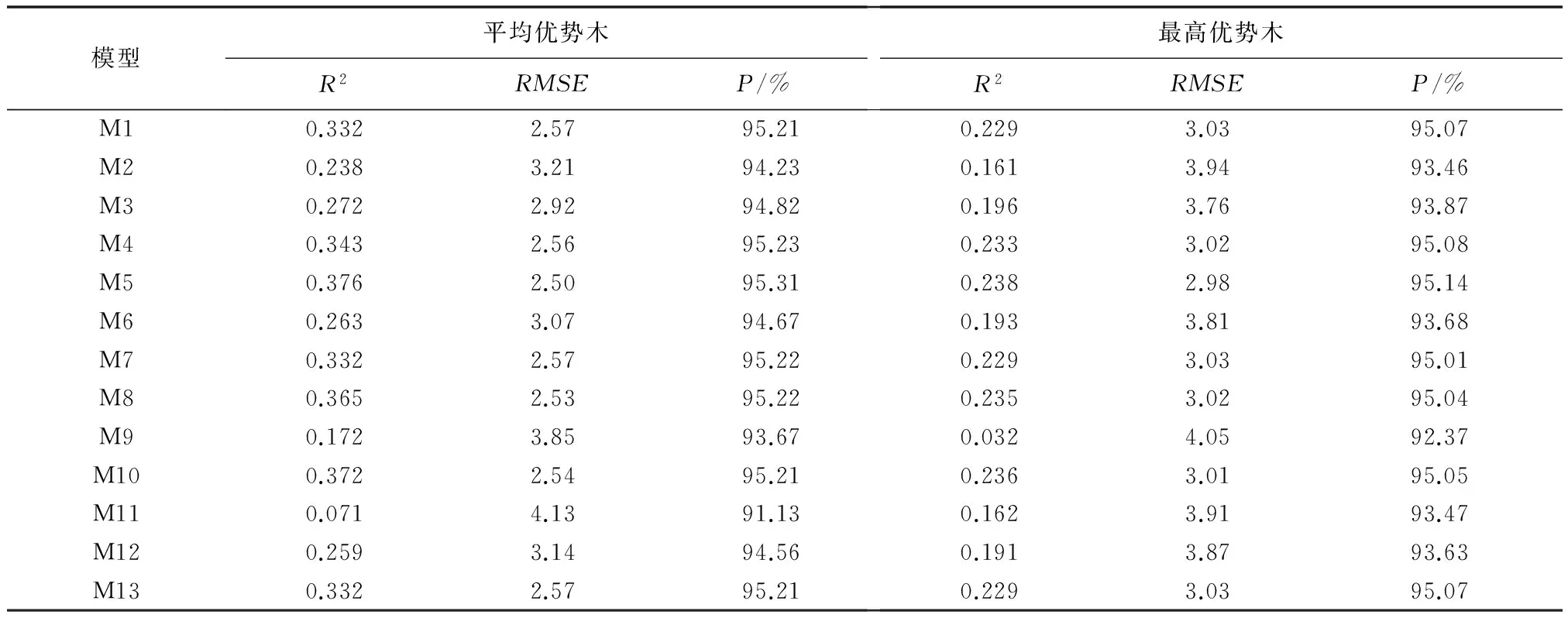
表4 基础模型

表5 不同参数拟合结果

3.2.2 立地类型哑变量拟合结果

基于平均优势木数据,根据51块样地初始划分的43个立地类型应用到模型M5拟合的得分值聚类,聚类精度≥0.99的标准下,得出聚类成8类时满足要求,聚类分类数对应的立地编号及数量如表6所示。

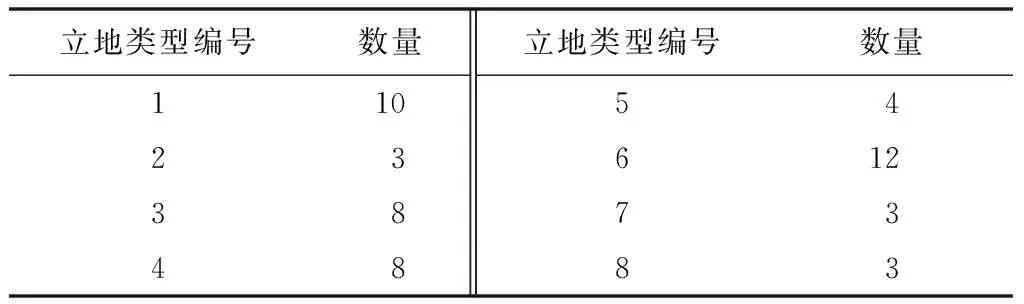
表6 立地类型聚类

将各样本的初始立地类型转换为对应的类,并作为哑变量加在候选模型上M5进行拟合分析。

以聚类后的立地类型为哑变量加在候选模型不同参数(a,b,ab)上拟合,得到模型M5的各个评价指标值(表7),根据4个评价指标选出候选模型立地类型最优参数形式。

表7 不同参数拟合结果

从表7可以看出,在加入立地类型哑变量后,平均优势高模型确定系数从0.376提高到0.939 5～0.977 5,哑变量同时加在参数a,b上时运行出现错误。哑变量加在模型M5参数a上的确定系数和预估精度最大,分别为0.977 5,99.14%,均方根误差和AIC最小,分别为0.46,101.50。

3.3 2种哑变量模型的对比分析

评价指标表明哑变量模型的拟合精度比基础模型的拟合精度高。另外,考虑立地类型效应比考虑林分类型效应的精度高。为了反映2种不同哑变量模型最优形式与基础模型之间的差异,以及不同哑变量模型之间的相容性,表8列出了基础模型M5的参数值,表9列出了平均优势高模型M5林分类型和立地类型哑变量最优参数形式拟合的参数估计值。

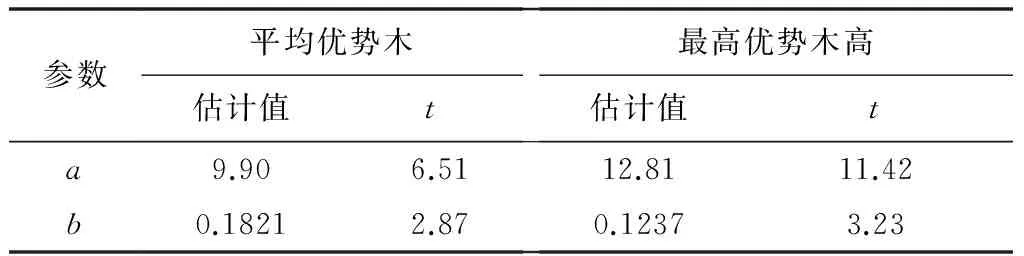
表8 基础模型参数值

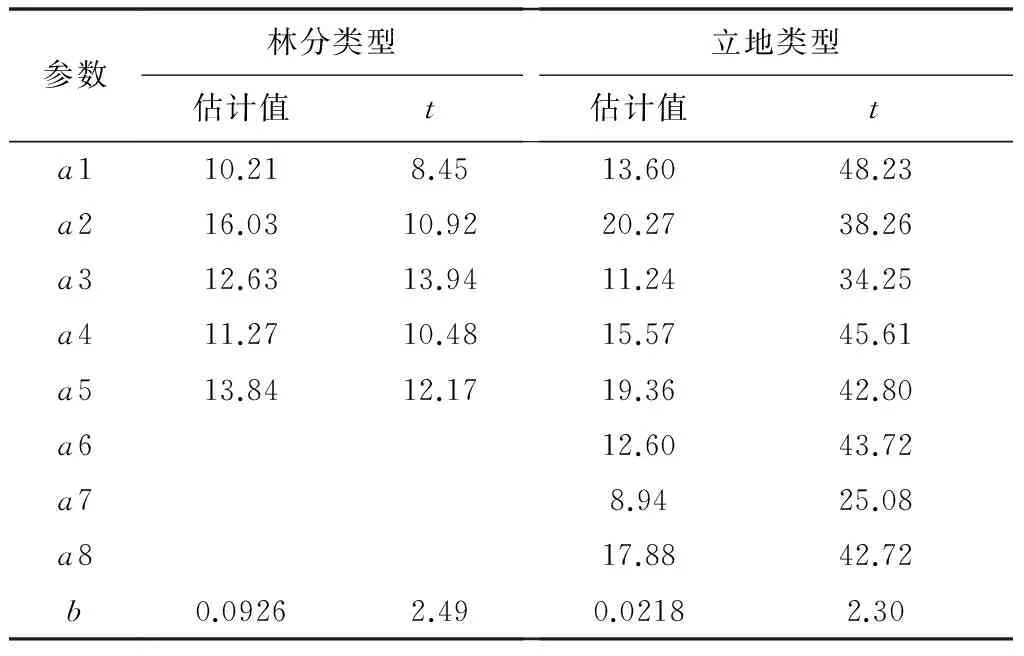
表9 哑变量模型参数估计

3.3.1 最优模型参数值估计

对于模型M5,基础模型和哑变量模型的所有参数值都较好。林分类型哑变量模型中哑变量参数估计值之间的差异要小于立地类型哑变量模型中哑变量参数估计值之间的差异,也就是说,在本研究中,立地类型哑变量模型所反映出来的各个立地类型之间的差异相比林分类型哑变量模型较好。另外,两种哑变量模型中的参数b都具有较好的通用性。

3.3.2 最优模型残差图

根据拟合结果,选出最优模型M5最佳哑变量参数形式。以树高预测值为横坐标,残差为纵坐标绘制残差图,得出模型M5分别以两种优势木拟合时基础模型的残差图(图1),平均优势高模型中林分类型哑变量和立地类型哑变量最优参数形式的残差图(图2)。

图1、图2直观地反映了哑变量模型方法的差异,图1表明平均优势木模型优于最高优势木模型。从图2可以看出:不论是林分类型哑变量模型还是立地类型哑变量模型,分别以林分类型、立地类型进行估计后的平均优势木残差图要优于基础模型残差图,立地类型哑变量模型优于林分类型哑变量模型。

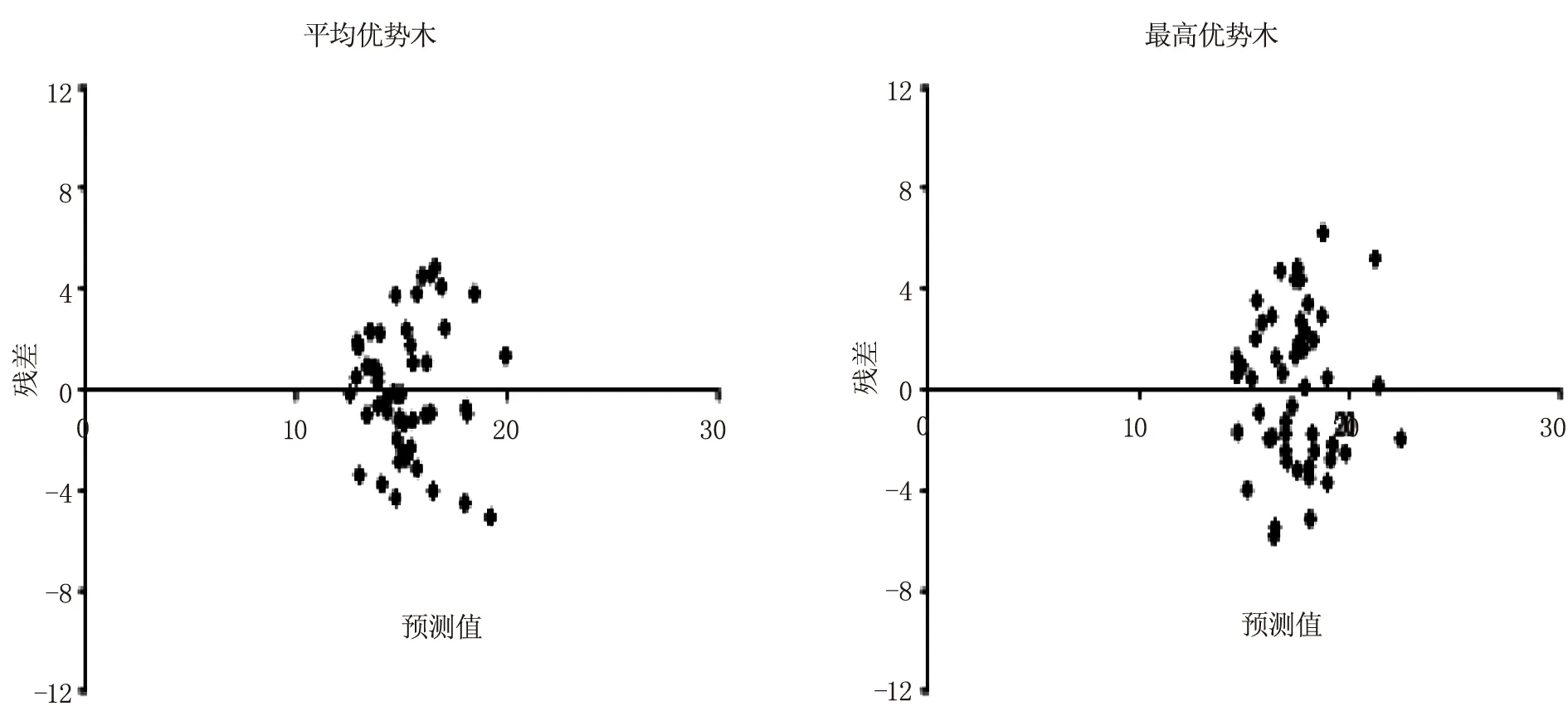
图1 基础模型残差图

图2 哑变量残差图

4 结论与讨论

由于本研究的数据采集局限于湖南5个地区,因此模型的适用范围有限。本研究在优势木选取上采用了两种常用的方法,就选取方法来说,平均优势木要比最高优势木复杂；但就拟合精度而言,平均优势木模型要优于最高优势木模型。在以后的研究中,还可尝试其它优势木的选取方法。对于立地类型哑变量,本研究中样地初始的立地类型没有包含湖南地区所有的栎类立地类型种类,因此,立地类型哑变量模型方法的应用存在局限性。文中采用R软件中k-means聚类方法,将初始立地类型聚类成几个类作为哑变量,简化哑变量类型的目的是为了探讨这种方法的应用,由于没有包括该地区的主要立地类型,其实用性需进一步探讨。

本研究考虑了立地与林分树种结构对栎类天然混交林树高曲线的影响,为区域性天然混交林树高曲线模型的研究提供了一种有效的思路与途径。

[1]Lei X D,Peng C H,Wang H Y,et al.Individual height-diameter models for young black spruce (Piceamariana) and jack pine (Pinusbanksiana) plantations in New Brunswick,Canada.[J].Forestry Chronicle,2009,85(1):43-56.

[2]Sharma M,Parton J.Height-diameter equations for boreal tree species in Ontario using a mixed-effects modeling approach[J].Forest Ecology & Management,2007,249(3):187-198.

[3]Colbert K C,Larsen D R,Lootens J R.Height-Diameter Equations for Thirteen Midwestern Bottomland Hardwood Species[J].Northern Journal of Applied Forestry,2002,19(4):171-176.

[4]Temesgen H,Gadow K V.Generalized height-diameter models—an application for major tree species in complex stands of interior British Columbia[J].European Journal of Forest Research,2004,123(1):45-51.

[5]Curtis R O.Height-Diameter and Height-Diameter-Age Equations For Second-Growth Douglas-Fir[J].Forest Science,1967,13(4):365-375.

[6]Huang S,Titus S J,Wiens D P.Comparison of nonlinear height-diameter functions for major Alberta tree species[J].Canadian Journal of Forest Research,1992,22(9):1297-1304.

[7]胥辉,全宏波,王斌.思茅松标准树高曲线的研究[J].西南林业大学学报,2000,20(2):74-77.

[8]袁晓红,李际平.杉木人工林南北坡向树高-胸径生长曲线研究[J].西北林学院学报,2012,27(2):180-183.

[9]樊艳文,王襄平,曾令兵,等.北京栓皮栎林胸径-树高相关生长关系的分析[J].北京林业大学学报,2011,33(6):146-150.

[10]田军.华北落叶松和樟子松树高与胸径的相关性研究[J].安徽农学通报,2011,17(22):72-72.

[11]赵俊卉,刘燕,张慧东,等.长白山天然林不同树种树高曲线对比研究[J].浙江农林大学学报,2009,26(6):865-869.

[12]赵俊卉,亢新刚,刘燕.长白山主要针叶树种最优树高曲线研究[J].北京林业大学学报,2009,31(4):13-18.

[13]李海奎,法蕾.基于分级的全国主要树种树高-胸径曲线模型[J].林业科学,2011,47(10):83-90.

[14]Huang S,Titus S J.An age-independent individual tree height prediction model for boreal spruce-aspen stands in Alberta[J].Canadian Journal of Forest Research,1994,24(7):1295-1301.

[15]Patricia A,Miren D R,Isabel C.A mixed nonlinear height-diameter model for pyrenean oak (Quercus pyrenaica Willd.)[J].Forest Ecology & Management,2008,256(1):88-98.

[16]陶用舒.论湖南人才的地理环境[J].湖南城市学院学报,2003(1):79-84.

[17]胡芳名,李建安,李若婷.湖南省主要橡子资源综合开发利用的研究[J].中南林学院学报,2000(4):41-45.

[18]祁承经,孙希儒.湖南壳斗科植物的研究[J].中南林学院学报,1987(1):1-17.

[19]刘振西.栎树资源及其开发利用[J].湖南林业科技,1994(3):64-66.

[20]Huang S,Titus S J.An index of site productivity for uneven-aged or mixed-species stands[J].Canadian Journal of Forest Research,1993,23(3):558-562.

[21]盂宪宇.测树学[M].北京:中国林业出版社,2006.

[22]王明亮,李希菲.非线性树高曲线模型的研究[J].林业科学研究,2000(1):78-82.

[23]Fast A J,Ducey M J.Height-Diameter Equations for Select New Hampshire Tree Species[J].Northern Journal of Applied Forestry,2011,28(3):157-160.

[24]王冬至,张冬燕,张志东,黄选瑞.基于非线性混合模型的针阔混交林树高与胸径关系[J].林业科学,2016(1):30-36.

[25]李希菲,洪玲霞.用哑变量法求算立地指数曲线族的研究[J].林业科学研究,1997,10(2):215-219

[26]唐守正,李勇.生物数学模型的统计学基础[M].北京:科学出版社,2002.

[27]李丽霞,郜艳晖,张瑛.哑变量在统计分析中的应用[J].数理医药学杂志,2006,19(1):51-52.

[28]唐守正,郎奎建,李海奎.统计和生物数学模型计算(ForStat教程)[M].北京:科学出版社,2008.

[29]李河,麦劲壮,肖敏,等.哑变量在Logistic回归模型中的应用[J].循证医学,2008,8(1):42-45.

Dominant Height-Diameter Models for Mixed Quercus Forest Based on Dummy Variable

ZHU Guangyu,LUO Xiaolang

(CentralSouthUniversityofForestryandTechnology,Changsha410004,China)