定向凝固Al2O3基共晶陶瓷

王伟男，刘俊成

定向凝固Al2O3基共晶陶瓷

王伟男，刘俊成

（天津工业大学材料科学与工程学院，天津 300380）

近年来，定向凝固Al2O3基共晶陶瓷由于具有优异的高温力学性能，成为研究重点。各国学者通过改进工艺，提高温度梯度，使其力学性能不断提高，并且对于陶瓷的凝固理论也在不断完善。介绍了国内外学者的工作进展，并对陶瓷凝固理论进行总结，指出了在保证力学性能的前提下，获得大尺寸的定向凝固共晶陶瓷是未来的研究重点。

定向凝固；Al2O3基；生长理论；力学性能

0 引 言

21世纪以来，随着航空航天行业的飞速发展，其对于超高温(≥1650 ℃)材料的需求越来越迫切。性能优良的超高温材料，可以使飞行器的发动机和涡轮机在超高温下正常工作时无需冷却系统，促进燃料充分燃烧，降低消耗，减少有害尾气(CO2、NOx等)的排放量，改善环境。定向凝固Al2O3基共晶陶瓷不存在孔洞和界面非晶相，因而大大提高了材料的力学性能[1]，并且其密度很小，高温下不会被氧化，有希望成为新一代超高温结构材料，近年来各国学者对此展开了大量研究。

通过定向凝固技术制备的共晶陶瓷，其具有几个基本优点：相与相界面结合良好、高温下组织不发生变化、孔洞率较低、几乎没有非晶相等。通过调整定向凝固法的各种工艺参数(温度梯度高低、生长速率、外加旋转等)可以调整陶瓷材料的显微组织，进一步提高性能[2]。

本文总结了国内外常用的定向凝固制备技术以及研究现状，并对其生长理论进行了归纳。

1 研究进展

通过定性凝固制备氧化物共晶陶瓷的研究始于20世纪60年代[3]。1969年，Viechnicki等人首先进行了Al2O3/Y3Al5O12(YAG)共晶陶瓷的定向凝固研究。但是由于当时实验设备条件的限制，没有得到预期的温度梯度，凝固组织中含有晶团，极大地影响了性能。20世纪末，有学者采用定向凝固法制备了氧化物共晶陶瓷，发现其性能非常优异[4]，吸引了世界各国对此开展研究，为材料领域的热点之一。日本Waku等人[4-5]对Bridgeman进行了改进，利用改进后的方法制备了Al2O3/YAG共晶陶瓷，利用电镜对其微观组织进行了表征，发现其晶粒分布均匀，主要为三维网状结构，不同相交织在一起[6]。利用这个方法所制备的以氧化铝为基的共晶陶瓷，其在高温下力学性能很优秀，此后其他国家的学者也对此展开大量研究。这种材料从室温到1800 ℃，在温度到达熔点，即1830 ℃，其抗弯强 度在350 MPa附近，是使用普通烧结法制备的同样成分材料的6倍以上；在1680 ℃下并使试样暴露在空气下，对其保温1000 h，发现其质量以及显微组织都没有发生变化，显示了良好的高温稳定性；在高温(＞1580 ℃)下，施加10-4/s的应变速率，这种材料的蠕变强度高达433 MPa，是使用普通烧结法制备的同样成分材料的13倍。在共晶反应中添加氧化锆后，Al2O3/Y2O3/ZrO2共晶陶瓷在上述同等条件下，发现其抗弯强度高达851 MPa，是使用普通烧结法制备的同样成分材料的57倍[7]。阅读近年国际上的文献，以日本学者Waku、西班牙Orera、美国Sayir等为代表对Al2O3基共晶陶瓷，通过定向凝固手段进行了大量研究[8-11]。

定向凝固法制备的Al2O3基共晶陶瓷，由于Al2O3性质更加稳定，不会发生相转变，具有更好的力学性能和高温抗氧化性能。目前，国内外学者研究集中在以下几个体系[12]：

(1)Al2O3/ZrO2系。为了稳定ZrO2相，在该体系加入Y2O3，Y2O3与ZrO2结合，形成伪二元共晶Al2O3/ZrO2(Y2O3)，通过调整氧化钇的含量，但注意不要过量，可以形成不同晶系，不同晶体取向的氧化锆，获得所需的性能。

(2)稀土元素系，例如Al2O3/(RE)AlO3系、Al2O3/(Re)Al5O12(EAG)。这里的Re通常为Sm、Eu、Gd、Er、Y等。一般为氧化铝的钙钛矿，其他情况为氧化铝与石榴石相结合的二元或者三元共晶。

(3)加大Y2O3含量，形成Al2O3/YAG/ZrO2三元共晶体系以及伪共晶体系。

在定向凝固技术制备氧化物共晶陶瓷的研究上，日本学者在国际上占据很大优势，主要领军人物Waku对Bridgeman法进行改善后，利用这种方法制备了许多成分配比不同的氧化铝基共晶陶瓷，之后又对其微观组织、高温下的力学性能做了很多研究[5-7]。Lee等人[13-14]采用微拉法(μ-PD)成功制备出直径为0．3-2 mm、长达500 mm的Al2O3/YAG、Al2O3/YAG/ZrO2，以及直径为5 mm、长60 mm的Al2O3/MgAl2O4高性能共晶陶瓷纤维，其中Al2O3/ YAG/ZrO2三相共晶陶瓷纤维在1200 ℃下高温强度达到970 MPa[15]。国外学者Calderon-Moreno[16]使用定向凝固技术中的熔体快速淬冷法制备了Al2O3/ Y2O3/ZrO2伪共晶氧化物陶瓷以及Y3Al5O12/ZrO2共晶氧化物陶瓷，并且对凝固过程中的凝固机理、不同相结合情况及力学性能进行了大量研究，其最后制备出的Al2O3/YAG/ZrO2共晶陶瓷的共晶层间距＜100 nm，KIC高达9．0 MPa·m1/2。Isobe[17]对Al2O3/ YAG熔凝行为进行了较为详细的研究，其使用电火花等离子体放电加热制备的Al2O3/YAG熔凝氧化物共晶陶瓷弯曲强度为693 MPa，硬度为17 GPa，KIC为3．8 MPa·m1/2。

Orera研究小组采用激光区熔法(LFZ)对Al2O3/ ZrO2以及Al2O3/ZrO2(Y2O3)共晶陶瓷的组织、晶体学取向进行了研究。其利用激光区熔法制备出的Al2O3/YAG共晶陶瓷的微观组织为棒状共晶，在1900 K下的测量弯曲强度，发现高达1．53 GPa[8]。

Sayir等采用激光悬浮区熔(LHFZ)技术手段制备了Al2O3/ZrO2(Y2O3)伪二元共晶、Al2O3/YAG二元共晶陶瓷，高温性能优异[9-10]。之后又利用边界外延生长法制备了Al2O3/YAG二元共晶陶瓷纤维，其直径为75 μm。美国NASA-Lewis研究中心的学者采用激光加热区熔法，成功制备Al2O3/YAG二元共晶自生复合纤维，对制备的样品在1400 ℃处理2 h，发现样品抗拉强度降低40%，为13 GPa，但是同样条件下处理200 h，其抗拉强度仍然损失很慢，仍有11 GPa。

傅恒志等[18-22]采用激光区熔高温梯度快速定向凝固技术从熔体中直接制备Al2O3/Y3Al5O12(YAG)共晶自生复合陶瓷，超高温度梯度1×106K/m。调节激光扫描速率和功率密度，Al2O3和YAG两相分布均匀且连续，呈现层片状，两相相互耦合的共晶结构，测量其层片间距，仅为1到2 μm之间，其硬度为19．5 GPa，断裂韧性为3．6 MPa·m1/2。加入ZrO2后，由于ZrO2相会发生相转变，对基体产生相增韧效果，其室温断裂韧性提高到8．0 MPa·m1/2。最近，张军等通过改进工艺，采用双面区熔法，观察其微观组织，发现在双面区熔界面处共晶组织生长连续均匀，相与相相互耦合，不存在非晶相。

赵忠民等[23-25]使用超重力自挤压辅助燃烧合成技术，成功制备出低缺陷大体积的Al2O3/ZrO2(Y2O3)共晶陶瓷，其试样硬度为(17．8±1．5) GPa，断裂韧性为(14．2±1．0) MPa·m1/2。其Al2O3/33ZrO2(4Y)样品显微结构以取向各异且纳微米t-ZrO2纤维三角对称镶嵌其上的棒状共晶团为基体，周围分布着t-ZrO2微米球晶；Al2O3/40ZrO2(4Y) 中t-ZrO2是基体相，α-Al2O3分布在基体相周围，微观组织呈现出不规则形状共晶形貌。材料的致密性很高，不存在气孔，由于ZrO2存在相转变，对基体有相增韧机制，同时材料内部存在小尺寸缺陷，使得共晶陶瓷的韧性大大提高。

2 共晶生长理论

最近二十年，为了改善微观组织、提高材料性能，定向凝固制备复合材料成为各国学者的研究热点。学者对于共晶合金凝固理论研究很早，经过长时间的修正补充，现在已经非常完善。而对非金属共晶材料的研究起步较晚，还没有系统成熟的理论。由于金属凝固理论现在比较完善，所以论文中常常将其应用于非金属材料的凝固过程，并参照实验结果进行一定的修正。

共晶反应之后，共晶物呈现出的微观形态多种多样，根据组织形态的不同，我们把它们称为规则共晶(即金属-金属共晶)以及非规则共晶(即非金属-金属共晶)。在这里规则共晶指的是组成相都为非小平面的相形成的共晶组织，非规则共晶指的是非小平面相-小平面相间形成的共晶组织。他们之间的分类标准是熔化熵的值。在共晶物的组成相的熔化熵比4R大的情况下，称之为小平面相，在组成相的熔化熵比4R小的情况下，是非小平面相[26]。

2.1 规则共晶

当共晶反应中两相的熔化熵都比4R小时(R为摩尔气体常数)，多为金属-金属相或者金属-金属间化合物，相组成一般为规则共晶(非小平面相-非小平面相)，其凝固界面在原子尺度上是粗糙的，微观组织形态又分为层片状和棒状两种[27]。

Jackson和Hunt两位国外学者通过大量研究、分析，提出了规则共晶生长理论模型[28]，经过后续学者的实验验证，其理论模型与实验结果比较符合，成为共晶组织研究理论的基础，被大量引用在定向凝固方向的论文里。

J-H理论有以下三种假设条件：

(1)固液界面在宏观上是平界面，没有凸起或者凹陷；

(2)共晶两相的生长速度相同，生长方向垂直于固液界面；

(3)固-液界面前沿的各相，在凝固过程中过冷度一样。

凝固过程满足以上假设，经过实验和计算，发现层片间距(λ)、晶体生长速率(ν)和过冷度ΔT三者存在如下关系：

在公式(1)、(2)中，K1、K2是常数，只要共晶体系的相不改变，K1、K2就不会改变。分析这两个公式可以发现，过冷度不变时候，通过上述公式可以计算出两个不同大小的层片间距。但根据共晶凝固过程中，层片间距过小会导致各相之间面积增大，从而使得界面能增加，阻碍片间距变小；层片间距过大时，随着传质过程中大量同一组分的融质偏聚，减少固-液界面前沿的过冷度，使层片间距减小。层片间距应该在一定范围内，变化不大。

在不改变生长速率ν的前提下，图1表示凝固界面前沿ΔT和共晶层片间距λ之间的关系。从图1中可以得出，在生长速率ν一定时，过冷度不能过高或者过低，要保持在一定范围，才能使共晶组织稳定生长，这样得到的共晶组织的层片间距值在λm－λM。前文提到的三种假设条件下J-H模型才有效，J-H模型在固-液界面前沿为平界面，没有突起或者凹陷，凝固后材料的微观形貌为较为规则的共晶组织情况下，与实验结果符合。这种理论并不适用于非规则共晶生长，此后各国学者进行了大量实验，通过与实验结果对比，进一步将J-H模型修改完善。

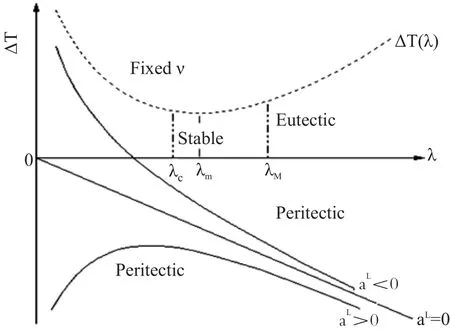
图1 生长速率V一定下凝固界面前沿过冷度ΔT与共晶层片间距λ的关系Fig.1 The relationship between interface under cooling ΔT and lamellar spacing λ for given growth velocity

图2 共晶反应中小平面相体积分数与溶解熵对组织形貌的影响(A为规则层片；B为规则棒状；C为不规则的分支层片；D为紊乱的薄片；E为复杂的规则结构；F为准规则结构；G为不规则的丝状结构)Fig.2 The effects on microstructure of eutectic small plane volume fraction and dissolving entropy

经过很多研究学者发现：在经典的共晶凝固理论中，没有考虑生长速率和杂质元素这两方面的影响，而实验结果表明，其对微观组织影响很大。Tiller等人研究了规则共晶组织显微形貌与生长速率大小之间的关系，在较高生长速率时，共晶组织呈现棒状；较低晶体生长速率下，一般出现层片状共晶组织[29]。Chadvick研究了固液界面形态及凝固时微观组织形态转变与杂质元素之间的关系。固液界面形态与共晶组织形态的转变有关，各相的体积分数可以影响固液界面形态，若共晶物中存在杂质元素，会改变固-液界面前沿的成分过冷，使固液界面的形态转变，固-液界面由平界面变为胞状界面，出现共晶团和棒状共晶组织[30]。

Maginin和Trivedi[31]选择适用的三相点平衡准则，通过改变三相点的位置来调节共晶不同相的体积分数，这种情况考虑了共晶相的密度差，等温界面条件消失，通过这种方法修正了曲率过冷度，修正后与实验结果基本符合。此后，Maginin和Kurz等人经过大量实验研究，在此前凝固理论的基础上建立了TMK模型，这个主要适用于快速定向凝固条件[32-34]。在生长速率比较大的快速定向凝固条件下，J-H理论模型不能适用这种情况，将不存在理想的按照理论规则生长的共晶组织。Hopkins等人[35-36]主要研究了熔体在液态下流动如何影响共晶组织形貌，其研究表明，熔体流动可以改变固液界面前沿上的浓度，如果传质受到影响，会造成局部成分偏析，生长方向发生改变，影响定向凝固后试样的微观组织形貌。

Karma等人[37]通过大量数学计算，科学的解释了共晶反应中不同相表面能之间的关系以及不稳定状态下的晶体生长过程，他认为动力学系数对不稳定状态下的晶体生长过程有着重要的影响，对共晶层片间距的选择机制有了比较合理的解释，形象的描述了缺陷在晶体生长过程如何影响片层间距的大小。Liu[38-42]等人通过模拟方法分析了共晶两相生长过程中为何会出现缺陷，他指出缺陷的主要作用是过冷度调整的需要，是由于溶质堆积到了凝固界面前沿产生的。为了修正和完善凝固理论模型，Liu等人做了的大量工作，并且使用模拟方法研究晶体生长，有力的推动了定向凝固技术的发展。

2.2 非规则共晶

当共晶体的一相熔化熵比4R高的情况下(一般为金属-非金属以及非金属-非金属间化合物共晶)，凝固时界面前沿为棱面，其在原子尺度上是光滑的，称为小平面。我们一般将小平面-小平面方式凝固的共晶称为非规则共晶，通过对其微观结构的观察，这类常出现不规则结构。在晶体生长过程中，由于小平面相的各向异性很强(如界面能、热传导、最优生长方向等)，固液界面上的生长方向为特定的晶面，其形态为非平面，这种界面是非常不规则的，并且等温面也是不平直的，所以共晶反应中小平面相的体积分数对凝固后的共晶形貌影响较大。

图2为在生长速率为5 μm/s的情况下，材料中以小平面相为生长方式的物相含量与其溶解熵值对共晶微观组织形貌的影响。此图是由Corker[12]所绘制的。在非规则共晶情况下，从图2可知，当小平面相的含量比10%要小的情况下，凝固后的共晶组织为层状结构；当小平面相的含量大于10%而小于20%时，凝固后的共晶组织为片状结构；当小平面相的体积分数20%-35%之间时，凝固后的共晶组织为复杂的规则结构。但是在共晶中小平面相含量比40%大的情况下，共晶反应凝固后的共晶组织一般为准规则结构。板片状或者少量的棒状一般是此类组织的非小平面相，凝固后的基体为小平面相。当液相中的温度梯度减少或者长大速度增加时，棒状结构的比例就会增加。当有第三组元的存在的时候，主要是侧向的棒状结构会有所增加，这时凝固过程就会促使形成胞状组织。

在规则共晶的基础上，Magnin[43-45]等人对非规则共晶的生长理论模型进行了补充：

(1)生长平面温度不同，是非等温界面；

(2)利用J-H模型计算得到λm，根据凝固界面稳定性和凝固界面形貌的判据来确定最大层片间距。经过实验修正补充，Magnin有了与J-H模型比较相似的公式：

这个理论模型与J-H不同的是出现了修正系数Φ，Φ由不同的共晶成分所决定。由于修正系数的变化比较大，这导致了非规则共晶凝固后微观组织的层片间距选择范围很大，还不能准确计算出层片间距。

3 结 论

(1)国内外对于定向凝固共晶陶瓷开展了大量研究，不断改进工艺，使得制备的共晶陶瓷具有很高的硬度、断裂韧性，但制备的共晶陶瓷尺寸较小且大部分为棒状，无法满足高温结构部件的要求，学者下一阶段的工作应在保证力学性能的前提下，制备尺寸较大的定向凝固共晶陶瓷。

(2)从共晶陶瓷生长理论来看，规则共晶的理论已经较为完善，而非规则共晶的理论研究并不是十分系统，而且理论与实验数据有时不相符，还需要学者进一步的实验和模拟计算来完善理论。

[1] ATTARIAN M, TAHERI A K． Microstructural evolution in creep aged of directionally solidified heat resistant HP-Nb steel alloyed with tungsten and nitrogen [J]． Materials Science & Engineering A, 2016, 659: 104-118．

[2] 陈昌明, 周万成, 张立同, 等 ．定向凝固陶瓷共晶复合材料[J]．材料导报,1996, 4: 74-78．

[3] WAKU Y． A new ceramic eutectic composite with high strength at 1873K [J]． Adv Mater,1998, 10(8): 615-617．

[4] YOSHIKAWA A, HASEGAWA K, LEE J H, et al． Phase identification of Al2O3/RE3Al5O12and Al2O3/REAlO3(RE=Sm-Lu, Y) eutectics [J]． Journal of Crystal Growth, 2000, 218: 67-73．

[5] WAKU Y, NAKAGAWA N, OHTSUBO H, et al． Fracture and deformation behavior of melt growth composites at very high temperatures [J]． J Mater Sci．, 2001, 36: 1585-1594．

[6] WAKU Y, NAKAGAWA N, WAKAMOTO T, et al． The creep and thermal stability characteristics of a unidirectionally solidified eutectic composite [J]． J Mater Sci．, 1998, 33: 4943-4951．

[7] WAKU Y, NAKAGAWA N, WAKAMOTO T, et al． A ductile ceramic eutectic composite with high strength at 1873 K [J]．Nature, 1997． 389: 49-52．

[8] SAYIR A, FARMER S C． The effect of the microstructure on mechanical properties of directionally solidified Al2O3/ ZrO2(Y2O3) eutectic [J]． Acta Materialia, 2000, 48(18-19): 4691-4697．

[9] FRAZER C S, DICKEY E C, SAYIR A． Crystallographic texture and orientation variants in Al2O3-Y3Al5O12directionally solidified eutectic crystals [J]． J Cryst Growth, 2001, 233(1-2): 187-195．

[10] BERGER M, SAYIR A． Directional solidification of Al2O3-Al2TiO5system [J]． J Eur Ceram Soc．, 2008, 28(12): 2411-2419．

[11]LEE J H, YOSHIKAWA A, KAIDEN H, et al． Microstructure of Y2O3doped Al2O3/ZrO2eutectic fibers grown by the micropulling-down method [J]． Journal of Crystal Growth, 2001, 231: 179-185．

[12] 傅恒志, 郭景杰, 刘林, 等． 先进材料定向凝固[M]．北京:科学出版社,2008．

[13] LEE J H, YOSHIKAWA A, FUKUDA T, et al． Growth and characterization of Al2O3/Y3Al5O12/ZrO2ternary eutectic fibers [J]． Journal of Crystal Growth, 2001, 231: 115-120．

[14]周玉． 陶瓷材料学[M]． 北京: 科学出版社, 2004: 206-316．

[15] HARADA Y, SUZUKI T, HIRANO K, et al． Environmental effects on ultra-high temperature creep behavior of directionally solidified oxide eutectic ceramics [J]． Journal of the European Ceramic Society, 2005, 25: 1275-1283．

[16] CALDERON-MORENO J M, YOSHIMURA M． Stabilization of zirconia lamellae in rapidly solidified alumina-zirconia eutectic composites [J]． Journal of the European Ceramic Society, 2005, 25: 1369-1372．

[17] ISOBE T, OMORI M, UCHIDA S． Journal of the European Ceramic Society, 2002, 22: 2261-2625．

[18] SU H J, ZHANG J, CUI C J． Rapid solidification behavior of Al2O3/Y3Al5O12(YAG) binary eutectic ceramic in situ composites [J]． Mater Sci Eng A, 2008: 479(1-2): 380-388．

[19] SU H J, ZHANG J, TIAN J J． Preparation and characterization of Al2O3/Y3Al5O12/ZrO2ternary hypoeutectic in situ composite by laser rapid solidification [J]． J Appl Phys, 2008, 104(2): 023 511．

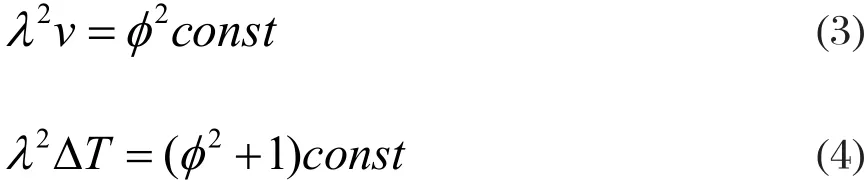
[20] SU H J, ZHANG J, CUI C J． Growth characteristic of Al2O3/ Y3Al5O12(YAG) eutectic ceramic in situ composites by laser rapid solidification [J]． J Alloy Compd, 2008, 456(1-2): 518-523．

[21] ZHANG J, SU H J, TANG B． Fractal characteristic of laser zone remelted Al2O3/YAG eutectic in situ composite [J]． Cryst Growth, 2008, 310(2): 490 -494．

[22] 苏海军,张军,刘林,等．定向凝固Al2O3/YAG共晶自生复合材料的组织形态及非规则共晶生长机制[J]．金属学报,2008,44(4): 457-462．

[23] 朱浩,赵忠民,张龙,等．超重力下燃烧合成Al2O3/ZrO2的成分结构和性能[J]．特种铸造及有色合金, 2009, 29(5): 455-458．

[24] 赵忠民,张龙,杨润泽,等．机械振动对燃烧合成Al2O3/ZrO2(3Y)自增韧复合陶瓷的影响[J]．稀有金属材料与工程, 2007, 36(增1): 724-726．

[25] 潘传增, 张龙, 赵忠民, 等．Al2O3/ZrO2(Y2O3)共晶复合陶瓷晶体生长机理[J]．粉末冶金材料科学与工程, 2007, 12(5): 290-295．

[26] 潘冶, 孙国雄． 共晶凝固的研究进展[J]．南京师大学报(工程技术版),2001,1(1):13-18．

[27] 李树军,李荣德．共晶凝固理论的研究与发展状况[J]．沈阳工业大学学报,2000,22(1):17-20．

[28] JACKSON K A, HUNT J D． Lamellar and rod eutectic growth [J]． Transition of Metall Society AIME, 1966, 236: 1129-1142．[29] TILLER W A． Liquid Metals Solidification [M]． Cleveland, Ohio: Am． Soc． Metals, 1958: 276．

[30] CHADWICK G A． Modification of lamellar eutectic structures [J]． Journal of the Institute of Metals, 1962-1963, 91: 298-303．[31] MAFNIN P, TRIVEDI R． Eutectic growth: A modification of the Jackson and Hunt theory [J]． Acta Metall Material, 1991, 39(4): 453-467．

[32] BOETTINGER W J, SHECHTMAN D, SCHAEFFER R J, et al． The effect of rapid solidification velocity on the microstructure of Ag-Cu alloys [J]． Metall． Trans．, 1984, 15A (1): 55-56．

[33] PEARSON D, VERHOEVEN J D． Forced velocity pearlite in high purity Fe-C alloys: Part 1． Experimental [J]． Metall．Trans．, 1984, 15A(6): 1037-1045．

[34] TRIVEDI R, MAGNIN P, KURZ W． Theory of eutectic growth under rapid solidification conditions [J]． Acta Metall, 1987, 35(4): 453-467．

[35] JIN J Z, KOBAYASHI K F, SHINGU P H． The effect of fluid flow on the eutectic lamellar spacing [J]． Met． Trans．, 1984, 15A(2): 307-312．

[36] HOPKINS R H, KRAFT R W． Nucleation growth of the Pb-Sn eutectic [J]． Met．, 1968, 242(8): 27-33．

[37] KARMA． Solidification Processing of Eutectic Alloys [M]．Am． Inst． Min． Engrs, 1988．

[38] LIU J, ELLIOTT R． A numerical model for eutectic spacing selection in the CBr4-C2Cl6 eutectic system [J]． J． Cryst．Growth, 1995, 148: 406-414．

[39] LIU J, ELLIOTT R． Self consistent solutions for lamellar eutectic growth [J]． Acta Metall． Mater．, 1995, 43(9): 3301-3311．[40] LIU J, ELLIOTT R． Eutectic spacing selection in the lead in eutectic system [J]． Metall． Mater．, 1995, 26A(2): 471～476．

[41] LIU J, ELLIOT R． Lamellar fault formation during eutectic growth [J]． J Cryst Growth, 1996, 162: 107-111．

[42] LIU J, ELLIOTT R． Irregular eutectic solidification [J]． Mater．Sci． Eng．, 1993, 173A: 129-132．

[43] MAGNIN P, MASON J T, TRIVEDI R． Growth of irregular eutectics and the Al-Si system [J]． Acta．Metall． Mater．, 1991, 39(4): 469-480．

[44] MAGNIN P, KURZ W． An analytical model of irregular eutectic growth and its application to Fe-C [J]． Acta Metall．, 1987, 35(5): 1119-1128．

[45] MAGNIN P, KURZ W． Competitive growth of stable and metastable Fe-C-x eutectics: Part II． Mechanisms [J]． Metall．Trans．, 1988, 19A(8): 1965-1971．

Preparation of the Directionally Solidif i ed Al2O3Based Eutectic Ceramics

WANG Weinan, Liu Juncheng (School of Materials Science and Engineering, Tianjin Polytechnic University ,Tianjin 300380,China)

In recent years, directionally solidif i ed Al2O3based eutectic ceramics have become the focus of research because of their excellent high-temperature mechanical properties. By improving the process and improving the temperature gradient, scholars of various countries have improved their mechanical properties. The growth theory of ceramics is constantly improving. The research progress of scholars is introduced and the ceramic solidif i cation theory are summarized. It is pointed out that it is the focus of the future research to obtain the large size directionally solidif i ed eutectic ceramics on the premise of ensuring the mechanical properties.

directionally solidif i ed, Al2O3based, growth theory, mechanical property

date:2017-03-06. Revised date: 2017-03-08.

TQ174.75

A

1006-2874(2017)03-0022-06

10.13958/j.cnki.ztcg.2017.03.005

2017-03-06。

2017-03-08。

刘俊成，男，教授。

Correspondent author: LIU Juncheng, male, Professor.

E-mail:3020152544@qq.com