考虑伤情分类的灾后创伤伤员救治与转运路径优化研究
2017-09-15刘昊天
王 晶,刘昊天,黄 钧
(1.北京工商大学商学院,北京 100048;2.中国科学院大学工程科学学院,北京 100049)
考虑伤情分类的灾后创伤伤员救治与转运路径优化研究
王 晶1,刘昊天1,黄 钧2
(1.北京工商大学商学院,北京 100048;2.中国科学院大学工程科学学院,北京 100049)
大规模自然灾害下极易产生大量创伤类伤员,对创伤伤员的快速抢救,是灾后救援工作的核心内容。为了实现大规模自然和事故灾难后伤员的快速救治与安置,提高救护车资源的利用率,本文提出了考虑伤员伤情分类的高效伤员救治与转运救援模式,即救护车对轻伤员实施就地救治,对重伤员进行转运医院后急救。根据伤员救治时效理论引入创伤指数计算等待期内轻重伤员的伤情变化,以伤员群体创伤指数之和最小作为优化目标,建立了多车程、需求可拆分的救护车VRP数学模型,并设计了基于车程的邻域搜索的模型快速求解算法,算例仿真和对比研究验证了模型和算法的有效性,给出了大规模自然与事故灾难后伤员分类救治与转运模式下的救护车路径方案。
伤员分类救治;多车程车辆路径问题;邻域搜索算法
1 引言
近年来城镇化的飞速发展使城镇地区的人口密集度不断增加,城市脆弱性也愈加明显,一旦发生大规模自然及事故灾难,将对当地人员的生命安全造成严重威胁。2013年4月20日,四川省雅安市芦山县发生里氏7.0级强烈地震,地震共计造成196人死亡,失踪21人,11470人受伤。其中成都军区总医院收治转运伤员65人,灾后24小时内收治伤员18人[1]。2015年8月12日天津瑞海公司危险品仓库发生火灾爆炸事故,造成798人受伤,其中伤情重及较重的伤员58人,轻伤员740人。这些大规模自然或事故灾害发生后短时间内伤员数量激增且分布范围广,伤员亟待救援,救护车数量相对于伤员数量明显不足,救援工作持续时间长且难度大。同时由于这类大规模突发事件的发生难以准确预测,无法事先做好充足的救援准备工作。因此,大规模自然和事故灾难后的快速反应并制定优化救援方案就显得尤为重要。
有关传统的伤病员急救转运问题的研究,主要建立救护车覆盖模型和路径最优化模型,提高救护车救援的有效性和及时性。如Knyazkov[2]研究了圣彼得堡市对急性冠心病人的急救转运工作的现状,并依据市区内路网状况提出了救护车路径优化建议,以提高居民人均拥有救护车数量和救护车反应速度;Coppi等[3]研究了传统医疗服务中对于病人转运区域规划和路径优化模型。张玲等[4]提出以最小化最大后悔值为目标构建应急救援网络。阮俊虎等[5]研究在大规模救援中对于关键救灾物资进行联合运送,保证救援的有效性。而大规模突发事件后应急救援与传统伤病员急救虽同属于伤员急救,但两者有很大差异,具体体现在创伤伤员人员数量多、救援范围广、救援持续时间长等诸多方面,导致大规模突发事件下伤员救援工作具有极高难度。目前关于大规模突发事件下伤员救援问题的研究主要包含以下两方面:救援方案优化目标函数的设计;建立合理的救护车指派或VRP模型描述灾后救援情景给出灾难情景下救护车路径规划。下面将结合这两方面介绍已有的研究文献。
众多学者对不同优化目标下的救护车指派问题进行了研究。杨文国等[6]指出在大规模伤员救援中,建立了伤员簇模型,以总加权救救援时间最短为目标求解救护车的最优指派问题。初翔等[7]以多灾点下总体死亡人数最小为目标,提出灾后医疗队支援指派决策方案,以5.12汶川大地震相关医疗数据统计文献为背景开展算例仿真研究。Mclay等[8]提出利用改进的马尔科夫决策模型对救护车调度进行动态优化,目标是最大化危重伤员救援数量。Knight等[9]依据威尔士地区的救护车服务数据,以最大化伤员生存数量为目标优化建立救护车辆指派模型,同时给出了伤员生存概率随时间下降的函数模型。袁媛等[10]考虑应急救援时间满意度和救援人员对急救任务的胜任程度,建立突发事件应急救援人员派遣的优化模型并给出有效解法。由转运伤员数量所引发的另一个问题是医院容量不足。对此,Yi Pengfei等[11]和Ma Guoxuan等[12]以最大化救护车和医疗资源使用效率为目标给出了伤员、救护车和医院之间的指派方案。从以上文献可以看出,选取一个贴近伤病员利益的目标函数以有效评估突发事件应急救援效果,是众多学者努力研究的方向。
应急资源指派模型可以解决救护车的分配问题,但在刻画伤员转运问题时有所不足,特别是在需要救护车多次医院往返转运伤员的情形下,需要研究救护车路径优化问题。灾后伤员转运路径优化问题可以归结为应急车辆路径优化问题,有学者在相关领域进行了研究工作,从不同角度应用数学方法进行车辆路径优化。Jotshi等[13]使用了车辆信息流更新的方法来研究灾后大规模分级伤员的医院转运问题,研究中对伤员进行了分类,且以伤员簇而非单个伤员作为路径节点,但救援方案对不同级别的伤员都进行转运后送进行救援。Talatico等[14]提出了对轻重伤员实行不同的救援方法,以加权等待时间最短为优化目标进行救护车救路径优化,并应用LNS算法求解。在救护车动态调度问题方面,Andersson[15]研究了救护车在完成当前转运任务后的动态再定位问题,以缩短救护车再次救援的反应时间。仿真结果证明其方法是有效的。
罗羽等[16]对国内外大规模突发事件下大批伤员救治与转运工作现状及救援流程进行了综述。他提出在制定救援方案前要首先对伤员进行验伤分类。为了更准确地评估震后伤员的存活情况,黄星等[17]利用伤员预测模型和SVM工具进行震后伤员存货量的预测。根据急救医学中救援时效性理论[18],重伤员的伤情恶化大多发生在伤后很短时间内,应尽可能使重伤员在“黄金急救时间”内接受救治,是降低其死亡率的一个关键;超出黄金急救时间之后,重伤员伤情指数变化将趋缓,逐渐失去急救价值。已有的研究模型目标函数多以救援任务完成总时间、伤员等待总时间或伤亡总人数最小为优化目标制定救援方案,不能满足对重伤员急救时效的要求;同时由于轻重伤员簇在空间分布中具有临近性,因此在制定救护车救治与转运车辆路径规划应对轻重伤员救治与转运进行统筹规划。目前有关救护车指派模型或路径优化的研究,模型相对比较简单,与实际大规模灾后救护车多次往返医院和伤员簇之间的救援情景差距较大,需要建立更加符合实际的模型以刻画灾后救援情景。
因此,本文在大规模突发事件的背景下考虑将轻重伤员分类救援。由于大规模灾害后产生的伤员大多为创伤伤员,故引入创伤指数(ISS)[19]描述轻伤员和危重伤员等待期内的伤情变化。模型中以伤员群体的伤情指数最小作为优化目标,动态调整轻重伤员在救援前期和后期被救援优先级别,统筹规划救护车救治与转运伤员的路径,使伤员群体在等待期内的伤情恶化程度降到最低。同时本文建立的多车程、需求可拆分VRP数学模型,并设计了基于车程的禁忌搜索模型求解算法,更符合大规模突发事件下救护车多次往返医院和伤员簇之间开展快速救援要求。
2 伤员分类救治与转运问题描述及数学模型
本文所提出的伤员就是方案是根据伤员伤情严重性,将伤员分为轻伤员和重伤员,救护车对轻伤员实施就地救治,对重伤员实施转运的救援方案。救护车救治与转运伤员问题的本质是解决救护车车辆路径规划问题。由于大规模灾后救援伤员数量较多,救护车多次往返医院和伤员簇进行救治和转运,因此需要对传统救护车路径优化问题进行改进,建立多车程的、需求可拆分的车辆路径优化问题。
2.1 救护车救治与转运伤员路径模式
在伤员救治与转运路径优化问题的背景下,多车程问题的层次结构比基本问题更加复杂。在基本VRP中,一辆车辆只行驶一个车程,因此车程与车辆的意义相同。而在多车程VRP中,如图2.1所示,一辆救护车的救援行驶计划中会包含多个车程,车辆与车程的含义不同,因此会形成多层次的解,包括救护车行驶计划、车程、伤员簇三个层次。车程作为连接救护车行驶计划层面和伤员簇层面之间关系的纽带,显得尤为关键。在单次车程中可能访问轻伤员簇、重伤员簇、医院三类节点,因此救护车的单次车程行驶方案可以归纳为几种基本路径模式。下面以一个模拟场景为例,演示实际救援中可能出现的救护车路径模式。
在该模拟情境中,S(Slightly)表示轻伤员簇,B(Badly)表示重伤员簇。当一个区域内同时包含轻、重伤员时,即为两个轻、重伤员簇位置相同。例如图2.1中,伤员簇B4和S4重合,表示该区域内混合了轻、重两种伤员。通过地理信息系统计算节点间的救护车行驶时间(B4和S4之间的行驶时间为零),以备求解问题。图1用箭线法标示出一种可行的救护车救治与转运路径方案。
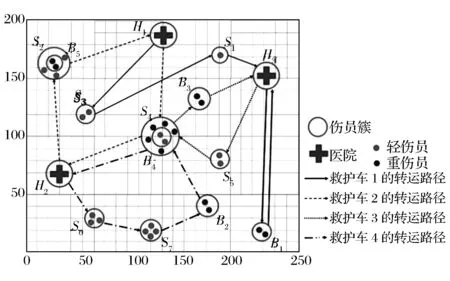
图1 模拟情景的一种可行救援方案
由该情景可以总结出所有可能出现的救护车路径模式,共有三种:
(1)医院→轻伤员簇→……→轻伤员族→医院
(2)医院→重伤员簇→……→重伤员族→医院
(3)医院→轻伤员簇→……→重伤员族→……→医院
如模拟情景的救援方案所示,救护车完成每一车程的救治和转运工作后返回医院,然后再由医院出发继续下批次工作。并且根据实际情况考虑,由于重伤员伤势危重,在救护车搭载重伤员后,不再访问轻伤员簇,只能继续访问重伤员簇转运重伤员或者直接返回医院。当一个重伤员簇内伤员数量超出救护车伤员容量上限的情况,救护车需多次访问该节点,以完成对全部伤员的转运工作。即一个伤员簇的救援需求可以被拆分。
2.2 伤员分类救治与转运数学模型
根据以上分析,建立考虑伤员伤情分类的救护车救治与转运路径规划数学模型。
模型中涉及的符号和参数如下:
B:重伤员(Badly injury)
S:轻伤员(Slightly injury)
P:所有伤员
H:医院
Kh:初始时刻医院内救护车数量,h∈H
K:所有参加救援工作的救护车
A:伤员、医院节点之间的弧
R:车程集合
tij:节点间行驶时间,(i,j)∈A
di:救护车对i点每一个轻伤员的救治时长,i∈S
dh:救护车到达医院后安置每名重伤员的时长,h∈H
ch:医院容量上限
ck:救护车容量上限
v:重伤员黄金急救时间
qi:伤员簇i的伤员数量
该模型设定决策变量如下:
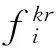
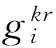
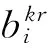
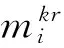
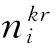
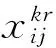
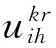
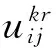
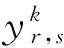
根据伤员分类救援方案和救护车转运与救治路径模式构建数学模型:
(1)
s.t.
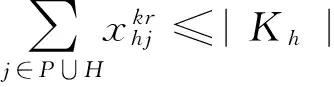
(2)
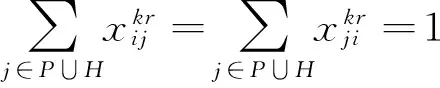
(3)
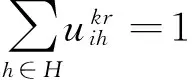
(4)
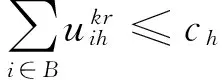
(5)
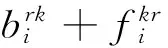
(6)
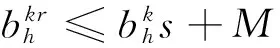
(7)

(8)
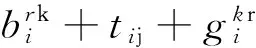
(9)
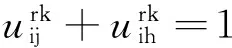
(10)
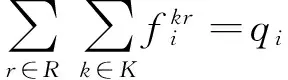
(11)
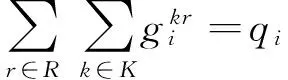
(12)
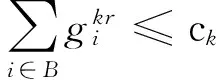
(13)
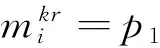
(14)
(15)
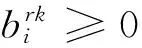
(16)
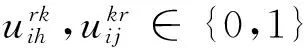
(17)
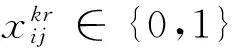
(18)
0 (19) 2.3 目标函数及约束说明 式(1)为目标函数,优化目标是使伤员群体在等待时间内的创伤指数总和最小;式(2)确保最初阶段至多有|Kh|辆救护车从医院h出发;式(3)保证伤员簇的输入流和输出流均为1,且救护车遍历每一个伤员簇;式(4)确保每个重伤员都被转运至医院;式(5)表示医院接收的重伤员数量不超过医院容量;式(6)确定救护车救治轻伤员后的行驶时间约束;式(7)保证每辆救护车行驶时间的连续性;式(8)刻画救护车到达重伤员簇的时刻;式(9)刻画救护车转运重伤员到达医院的时刻;式(10)表示救护车离开重伤员簇后只能到达下一重伤员簇或医院;式(11)和式(12)保证每一个伤员簇内的所有伤员都被救治或转运;式(13)表示救护车容量约束; 根据上文建立的数学模型可知,该问题是传统VRP问题的变形,为多车程,需求可拆分的车辆路径优化问题,属于NP-难问题,用精确解法很难得到最优解,需要采用启发式算法进行求解。在各类启发式算法中,禁忌搜索算法能够跳出局部最优解,保证后期的收敛性,是一种优秀的算法。 在解决单车程VRP的禁忌搜索算法中常对需求点编码生成搜索算子,但由于一辆救护车的行驶计划可能包含多个车程,因此这种编码方式不适于应用在解决多车程VRP的启发式算法中。本文设计了基于车程的禁忌搜索算法求解数学模型。该算法的关键是引入车程池集合,用于保存优质问题解的车程和生成新的车程,并设计针对车程的搜索算子和搜索策略,其流程主要包括车程构建过程、车程分配过程和车程池更新过程等。其流程图如图3.1所示。本节将对各流程进行说明。 3.1 车程构建过程 本文研究中以伤员簇作为需求节点,簇内伤员数量可能超过救护车容量,因此在生成初始解之前需要对网络中超过救护车容量的伤员簇节点拆分为多个子伤员簇,使每个子伤员簇的伤员数量不超过救护车容量ck。在本研究中救护车只对重伤员进行转运,而对救治轻伤员的数量没有限制,所以在构造初始解时只需对不满足要求的重伤员簇进行拆分。具体的车程构建过程如下: 步骤一:对不满足要求的重伤员簇进行拆分,直到所有重伤员簇内的伤员数量均小于等于救护车容量ck; 步骤二:将所有节点(伤员簇、医院)连接成一条大TSP路径。根据救护车路径模式的要求,大TSP路径中所有重伤员簇节点后不能访问轻伤员簇节点,且只有医院节点可以被重复访问。 步骤三:对大TSP路径进行切割,要求每段车程的首尾节点均为医院节点,生成一个车程集合作为初始解。 3.2 车程分配过程 车程分配过程是将当前给定的车程集合IR中的所有车程有效的分配到有限的车辆中去。生成各车辆行驶计划,每辆救护车要按照行驶计划顺序执行多条车程任务。 在基于车程的禁忌搜索算法中,每当新的车程IR集合生成,都要执行车程分配过程来生成所有车辆的行驶计划,即问题的解s并根据公式(1)计算s对应的伤员创伤指数和Z(s)。车程分配过程的算法需要能在较短时间内得到较优的车程分配方案。算法流程如下 步骤一:初始化所有车辆的行驶计划集合KS为空,依次将IR中的车程加入到各辆车的行驶计划中。 步骤二:重复步骤一直到IR中的所有车程被分配完毕。 3.3 邻域搜索过程 邻域搜索过程将作用于当前问题解s和它对应的车程集合IR,循环迭代搜索以求得最优解。对车程算子的扰动方法,本文参考Mohamed Cheikh[20]等的研究,主要包括针对伤员簇节点和车程的插入和交换操作,两种扰动方法按一定概率随机发生。进行扰动操作后得到的新车程,需要进行可行性检测。如果没有违反路径模式限定、车辆容量限制和医院容量限制等约束条件,将被保存,否则被丢弃。为了降低算法计算量,节点扰动后得到的新车程时间弧长度若大于原车程弧长的30%,则在检查可行性之前就摒弃该解。通过邻域搜索过程找出新的最优车程集合加入到车程池RP中。车程池中最多容纳pmax个车程,通过搜索迭代不断淘汰较差的解,保持车程池内解的优质性。 3.4 车程选择过程 当车程池RP己满时,用于进行邻域搜索的车程集合不再由车程构建过程随机生成,而会使用车程选择过程直接从车程池中生成,其算法流程为 步骤一:复制车程池RP′=RP,设置当前车程集合IR为空。 步骤二:按一定概率pr从RP′中选择车程r并将其从RP′中删除。 (20) 其中i为车程r在RP中的排位。 步骤三:将车程r插入IR。 步骤四:删除RP′中所有与车程r有共同服务顾客节点的车程。 步骤五:如果当前车程已经救援所有伤员,则跳转到步骤八,否则继续执行。 步骤六:如果RP′≠∅,则跳转到步骤二,否则继续执行。 步骤七:将IR中所有没有服务到的伤员节 点生成随机序列,使用车程构建过程生成新的车程集合,并插入到IR中。 步骤八:输出车程集合IR。 式(20)保证了越优质的问题解包含的车程被选择的概率越大。车程选择过程能在车程池内优中选优,不断提高解的质量。综上所述,基于车程的禁忌搜索算法流程总结如下: 图2 基于车程的禁忌搜索算法流程示意图 本算例情景设定为四川省雅安市区发生大规模突地震灾害,选取市内五家主要医院参与救援工作,伤员簇位置依据市区人口分布确定。设定灾后市区受灾范围较大且伤员在小区域内密集分布,共十个轻伤员簇,轻伤员七十一名;七个重伤员簇,重伤员共四十五名。轻伤员与重伤员数量比例为5∶3,符合灾后实际情况。医院和伤员簇的位置如图4.1所示。图中医院节点名称和每家医院内初始救护车标号和数量如表4.1所示。各节点之间时间弧根据地理距离估算得出(假定各辆救护车平均行驶速度相同,每两节点之间均连通),归纳到表4.2中。医院容量和各节点伤员数量已在图例中标出。设置相应参数并应用双层领域搜索算法求解该算例的救护车最优转运路径。 图3 模拟雅安市区灾后情景示意图 节点名称医院名称初始容纳救护车数量初始容纳救护车编号H1雅安市人民医院3K1、K2、K2H2雅安市第二人民医院2K4、K5H3红十字医院1K6H4雅安第四人民医院2K7、K8H5雅安市人民医院第三院区2K9、K10 本算例考虑重伤员的伤势都比较危重,设定黄金急救时间为60分钟。重伤员在黄金急救时间内的创伤指数增长速度p2=3,超出黄金时间后创伤指数增长速度p3=0.5。轻伤员的创伤指数增长速 度恒为p1=1。轻重伤员的创伤指数随时间变化的函数图像如图4.1所示。每辆救护车可容纳两名重伤员。救治每个轻伤员的时间和在医院安置每个重伤员的时间均为一分钟.禁忌步长itermax设定为5,车程池解容量为5。应用基于车程的邻域搜索算法对该算例求解,得到的十辆救护车救治与转运路径方案如表4.3所示。 图3 两类伤员的创伤指数随时间变化图像 除以最小化创伤指数和为目标之外,本文还以最小化救援时间、最小化伤员加权等待时间和为优化目标对上文的算例进行路径优化,求得其对应的伤员创伤指数和,并对三套救援方案对比分析。 表2 两节点之间救护车行驶时间汇总表(单位:分钟) 表2 创伤指数最小优化目标下的算例优化结果 从救援过程来看,当不考虑轻重伤员的差别,仅以最小化救援时间为目标进行优化时,重伤员在救援初期的急救需求易被搁置;以最小化轻重伤员加权等待总时间进行优化时,救援方案首先全部以重伤员为施救目标,其中包含超出黄金急救时间的重伤员,挤占属于轻伤员的急救车资源。在以最小化创伤指数为目标进行优化时,实际上动态调整了轻重伤员在救援前期和后期的救助优先级,超出黄金急救时间的重伤员会被安排 表4.4 不同优化目标下的伤员创伤指数结果对比 救援末期再转运。从救援效果来看,如表4.4所示,以最小化伤员创伤指数为优化目标,相比于以其他两个目标进行优化,伤员群体的创伤指数更低,表明该优化目标更符合伤员群体的利益。对目标函数值的对比结果表明,对伤员实行分类救治及转运的方法能够提高救护车的使用效率,降低伤员群体的受伤程度。 本文研究了考虑伤情分类的灾后创伤伤员大规模突发事件中救护车救治与转运路径优化问题。提出了针对不同伤情的伤员采用不同的方法进行救援的新模式,即对轻伤员在原地救治以稳定伤情,对重伤员则转运至医院进行急救,极大提高救护车的使用效率。本文引入创伤指数描述伤员伤情随等待时间的变化,以伤员群体创伤指数之和最小作为优化目标,动态调整了轻重伤员在救援前期和后期被救援优先级别,更好的描述了实际灾后救援的要求。同时考虑大规模突发事件灾情的特点设定伤员簇作为伤员节点,建立了多车程、需求可拆分的救护车VRP模型并针对模型的特点设计基于车程的邻域搜索的算法,将本模型求解的方案与已有研究中救援优化问题方案的进行结果对比,显示了伤员分类救援模式对降低伤员群体受伤程度的有效性。 本文提出模型与算法以期为大规模突发事件下伤员分类救治与转运的救护车路径优化问题提供决策参考。与单纯以缩短救援时间为目标的方案相比,本文提出的救援方法兼顾了轻重伤员的不同需求,能够更加有效地降低灾区内伤员群体的总体损失,适应于大规模突发事件灾难情景。模型中的参数可以根据不同灾害的特征进 行修改,具有良好的适应性和可扩展性。然而,本研究没有考虑到灾后救援中有关路网、伤员、救护车辆等由于灾难所带来影响和动态变化因素,后续研究还应加入道路可靠性和伤员数量不确定性等因素,使模型更好的描述灾后大规模伤员救援的实际情况。对于本文提出创伤指数的计算仅考虑伤员伤情随救援等待时间的变化,如何针对灾难特性和救援医学的研究对创伤指数计算进行改进,以更好地贴近实际情况将成为后续研究内容。此外,对于求解模型的算法也需要进一步优化改进,提高算法效率。 [1] 李运明,顾建文,郑驰,等.芦山地震住院伤员伤情和转运方式调查[J].中国询证医学杂志, 2013,13(12):1397-1400. [2] Knyazkov K, Oerevitsky I,Mednikov L,et al. Evaluation of dynamic ambulance routing for the transportation of patients with acute coronary syndrome in Saint-Petersburg [J].Procedia Computer Science,2015,66:419-428. [3] Coppi A, Detti P, Raffaelli J. A planning and routing model for patient transportation in health care[J].Elevtronic Notes in Discrete Mathematics. 2013,41:125-132. [4] 张玲,陈涛,黄钧,基于最小最大后悔值的应急救灾网络构建鲁棒优化模型与算法[J].中国管理科学,2014,22(7),131-139. [5] 阮俊虎,王旭坪,杨挺,大规模灾害中基于聚类的医疗物资联合运送优化[J].中国管理科学,2014,22(10),80-89. [6] 杨文国,黄钧,郭田德.大规模突发事件中伤员救助的救护车分配优化模型[J].系统工程理论与实践,2010,30(7):1218-1223. [7] 初翔,仲秋雁,曲毅.基于最大幸福原则的多受灾点医疗队支援指派模型[J].系统工程,2015,33(10):149-154. [8] Mclay L A, Mayorga M E. A model for optimally dispatching ambulances to emergencyalls with classification errors in patient priorities [J]. IIE Transactions,2013, 45(1):1-24. [9] Knightn V A, Harper P R, Smith L.Ambulance allocation for maximal survival with heterogeneous outcome measures[J].Omega,2012,40:918-926. [10] 袁媛,樊治平,刘洋.突发事件应急救援人员的派遣模型研究[J].中国管理科学,2013,21(2),152-159. [11] Yi Pengfei, George S K, Paul J A,et al.Hospital capacity planning for disaster emergency management[J]. Socio-Economic Planning Sciences,2010,44(3):151-160. [12] Ma Guoxuan, Demeulemeester E. A multilevel integrative approach to hospital case mix and capacity planning[J]. Computers & Operations Research.2013,40(9):2198-2207. [13] Jotshi A, Gong Qiang, Batta R.Dispatching and routing of emergency vehicles in disaster mitigation using data fusion[J]. Socio-Economic Planning Sciences, 2009, 43(1): 1-24. [14] Talarico L, Meisel F, Sörensen K. Ambulance routing for disaster response with patient groups[J].Computers & Operations Research,2015,56:120-133. [15] Andersson T, Värbrand P. Decision support tools for ambulance dispatch and relocation[J].The Journal Operational Research Society,2007,58(2):195-201. [16] 罗羽,杨雅娜,刘秀娜,等. 重大灾害后大批伤员转运工作的研究现状[J].护理学杂志, 2009,24(2):87-89. [17] 黄星,袁明,王绍玉.基于Mexican Wv-SVM的震灾人员存活量模型[J].中国管理科学,2016,24(9),140-146. [18] 何忠杰.论急救的时效性[J]. 中国急救医学,2008,28(7):659-661. [19] 朱佩芳.损伤严重程度评分的演进[J].中华创伤杂志, 2005, 21(1):36-39. [20] Cheikh M,Ratli M,Mkaouar O,et al. A variable neighborhood search algorithm for the vehicle routing problem with multiple trips [J].Electronic Notes in Discrete Mathematics,2015,47:277-284. Research on the Route Optimization of Ambulance Treatment and Transportation after Disaster Based on the Injured Classification WANG Jing1, LIU Hao-tian1, Huang Jun2 (1.School of business, Beijing Technology and Business University, Beijing 100048,China;2.College of Engineering Science, Chinese Academy of Sciences, Beijing 100049,China) The rescue of the wounded after the disaster is the core of the post disaster relief work. The number of ambulances compared to the quantity of casualties is obviously insufficient,so the rescue to the wounded is very difficult. However, the severity of the wounded is on the different level. According to “Emergency Time Window” theory, rescuing those who are badly wounded in the first hours after disaster can greatly improve their chance of survival. Beyond the “Emergency Time Window”, the badly wounded have less rescuing value than the slightly wounded gradually. In short, the wounded should be classified according to their different characteristics and ambulance resources should be coordinated. In this context, in order to achieve rapid treatment and placement of the wounded in large-scale disaster, and improve the utilization rate of ambulance resources, the triage treatment and transportation rescue mode, namely taking local treatment to the slightly injury and transporting the badly wounded into hospital by ambulances is proposed. Trauma index is used to calculate the change of the severity of the wounded during the waiting period. The optimization goal is to minimize the trauma index of all wounded, and the Multi-Trip, Split-Demand ambulance VRP mathematical model(MTSD-VRP) is established. Based on the aboveissues, an approach base-on tabu search algorithm considering vehicle trips is developed for ambulance path optimization. The algorithm uses the “vehicle trip pool” to preserve the trips in better solution and generate new trips, and design the search operator and search strategy based on the trip. The algorithm flow mainly includes the trip generating process, the trip distribution process and the trip refreshing process. The simulation result shows that the MTSDVRP model and the tabu search algorithm is suitable for ambulance path optimization with wounded classification. The data used in numerical simulation is primarily references to the actual situation of Ya'an City, Sichuan Province. The MTS-DVRP model with wounded classification and the tabu search algorithm based on the vehicle trip can be used as reference for other related studies. wounded’s classification; multi-trip routing problem; tabu search algorithm 1003-207(2017)08-0114-09 10.16381/j.cnki.issn1003-207x.2017.08.012 2016-06-10; 2017-03-15 国家自然科学基金资助项目(91324012);北京市属高校青年拔尖人才培育计划项目;北京工商大学研究生科研能力提升计划项目 王晶(1982-),男(回族),河北邯郸人,北京工商大学生商学院副教授,博士,研究方向:应急物流、决策理论与方法,E-mail:wangjingjob2010@126.com. F251 A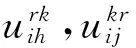
3 基于车程的禁忌搜索模型求解算法
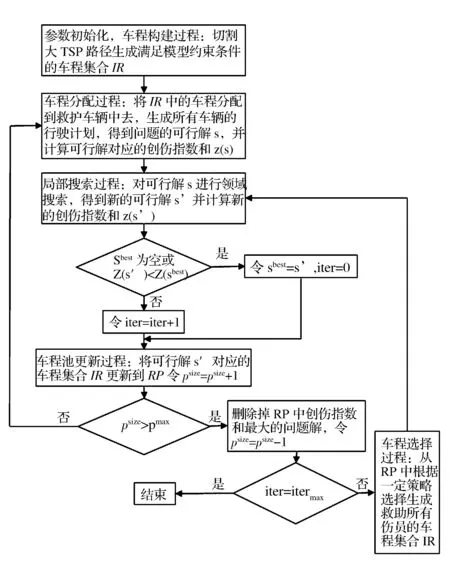
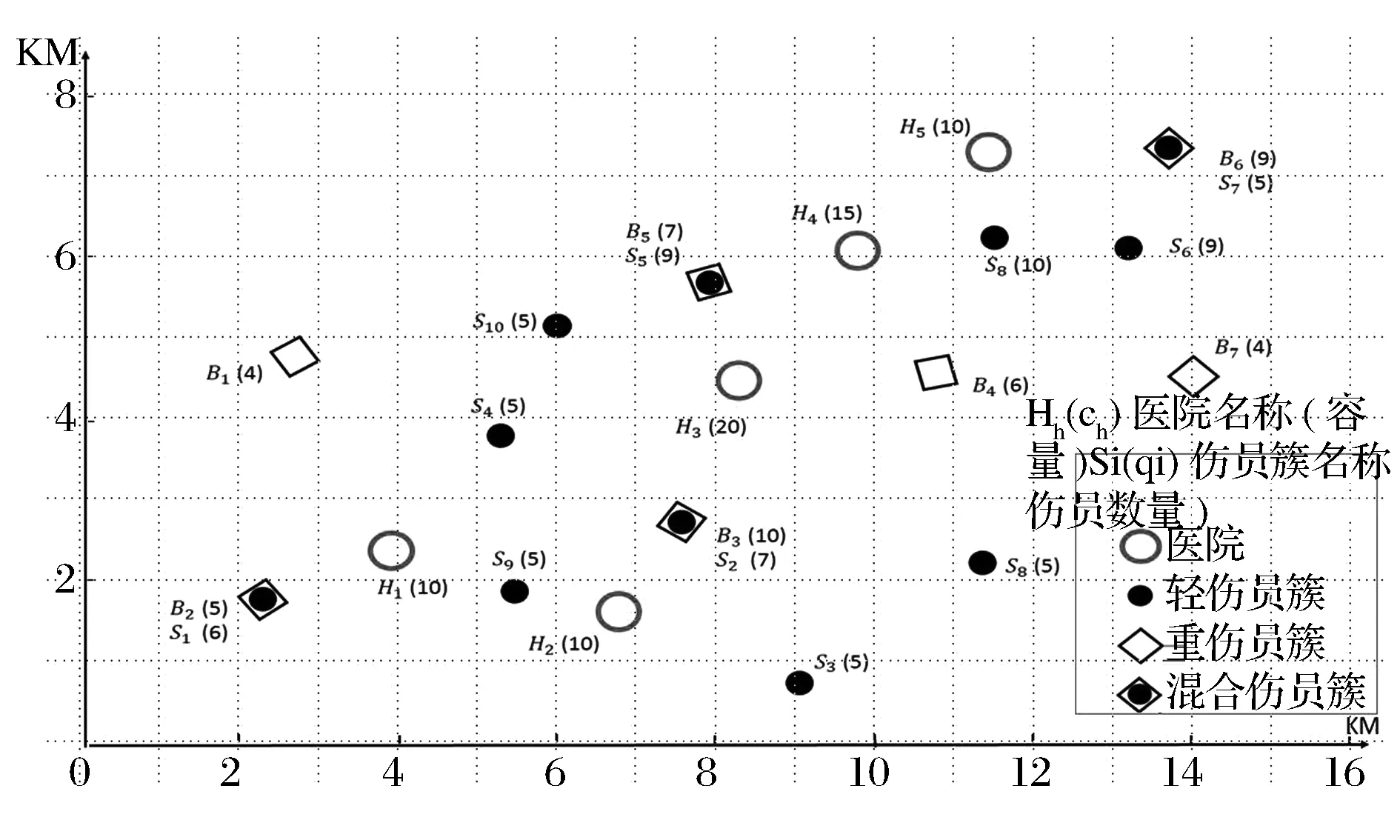
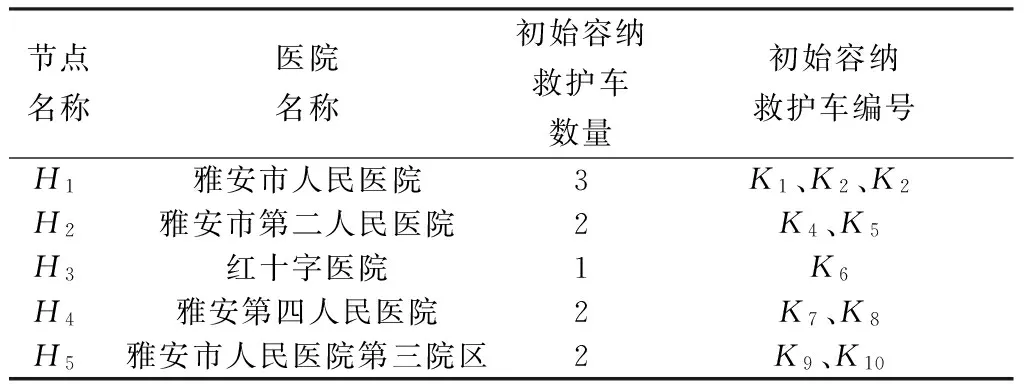
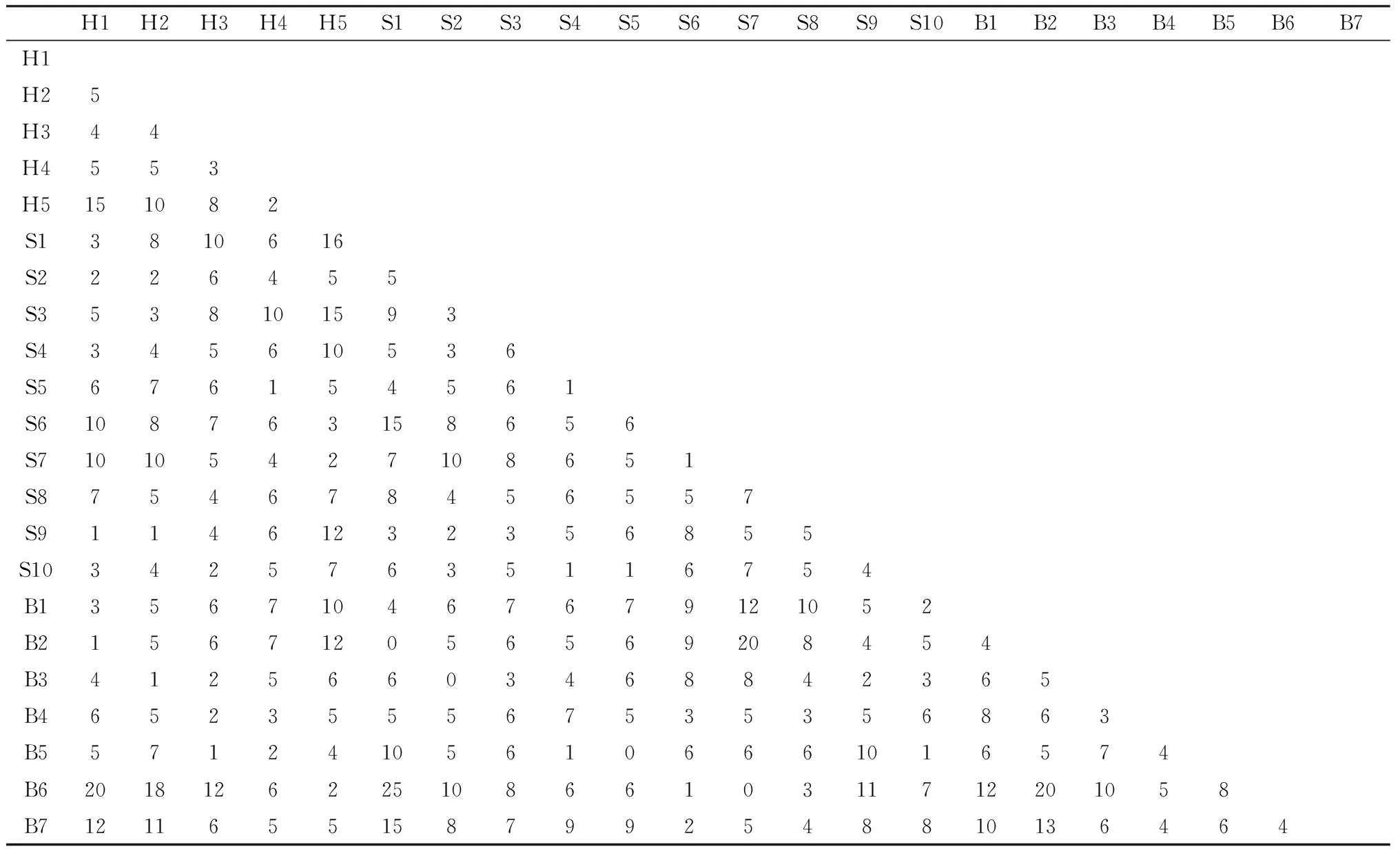
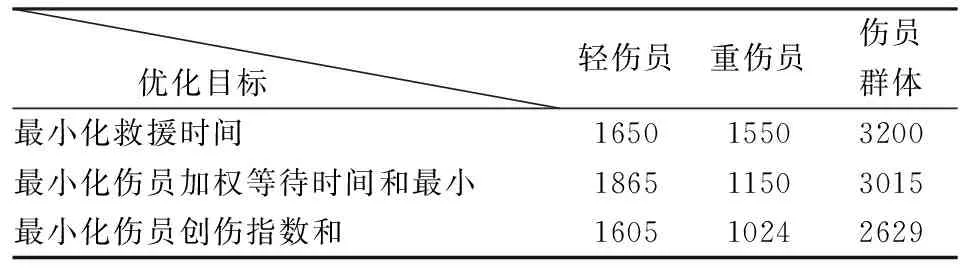
4 算例仿真


5 结语
