处于静态中带电平面导体电荷分布概率的计算
2017-09-14北京北方长城光电仪器有限公司徐卫星
北京北方长城光电仪器有限公司 徐卫星
处于静态中带电平面导体电荷分布概率的计算
北京北方长城光电仪器有限公司 徐卫星
为了能够了解导体内电荷的分布概况,利用麦克斯韦方程组中电场积分式,令其电场强度与闭环回路(或封闭空间)的积分和为零的理念,建立坐标模型和数学模型进行运算求得分布概率结果所采用的一种方法。
麦克斯韦方程积分式;导体内电场强度处处为零;电荷分布概率
引言
上一篇论文阐述了对线性带电导体电荷分布概率的计算方法,本次继续论述关于平面导体电荷分布概率的计算。( 上一篇论文发表在《电子技术与软件工程》2016年16期第138页 国际刊号ISSN 2095-5650)。
1. 为了更好地描述这种方法先阐述几个基本概念
1.1 平面分割:为了便于计算将被计算导体平面按照其平面特性分割成数块小面积。一般是按照平面的轴向方向与径向方向分割成数块边长为2△的正方形。注意:1)分割后平面必须不漏任何空余处。2)分割的面积尽量一致,否则影响计算精确度,特别是对电荷密度进行相对比较的块。3)测试方向两端必须存有连续中心电荷点,否则无意义。)
1.2 平面轴向方向:在进行平面分割时一般将平面较长的方向定为平面轴向方向。
1.3 平面径向方向:在进行平面分割时一般将平面较短的方向定为平面径向方向。
1.4 中心电荷点:在分割的小面积中选取某一点,此点可代表此分割面积的电荷集合量及其电荷集合量产生的电场对测试点的作用力,一般选在平面分割的中心范围内。
1.5 中心电荷线(带):在分割带状平面时往往分割成数条轴向的条形带,在带中取一条线,此线可代表此分割带的电荷集合量及其电荷集合量产生的电场对测试点的作用力,一般选在分割带的中间轴向直线。
1.6 测试方向:在导体平面中沿着径向和轴向方向上,在测试点处,设定的电场力的方向。
1.7 测试点:在导体平面中沿着径向和轴向方向上,在中心电荷点之间设定测试电荷的测量点。(q为尽小影响环境电场的电荷量)
2. 证明论述
2.1 计算方法:将任意平面的带电导体分划出n多个小面积(一般为边长是2△的正方形)将n多个凡是存有电荷小面积中的电荷量,集中在选定的各自小面积中的中心电荷点处。n多个中心点电荷的相互电场力可利用库仑定律建立函数关系。再经过合力分解方法转化为两条互相垂直的线性上,令其处处为零。解出各小面积的电荷量,从而求得各自密度值。
2.2 计算步骤:在任意平面的带电导体中任意划分二条间距2△的平行线,在二平行线中取n多个边长2△的正方形,直至导体的边缘。将二平行线以同样方法上下外延m多个平行线,直至导体的边缘。并取得n×m个边长2△的正方形。在含有导体的小正方形中心确定中心电荷点。(因导体往往处于不规则形状,会有小正方形中没有导体存在)利用库仑定律建立出每个中心电荷点相互作用力的关系,并分解为水平分量(或垂直)和垂直分量(或水平)。建立测试点使其各自为零。推算出各个电荷量,便求得电荷分布概率。即:

(i=1、2、3…n,j=1、2、3…m),σij为电荷密度,Qij为中心电荷点电量,S为导体面积。
2.3 可行性论证:在平面导体中任取一个分割小面积,此处为某一小正方形。如图1当求得测试点q1、q2、q3、q4都为零时q0测试点处必为零。其它小正方形具有同理。而当n→∞,时,因导体是连续、电荷分布是连续,所以任意点处在平衡状态下是无电场力和电荷移动的存在,任何闭环的积分必为零。
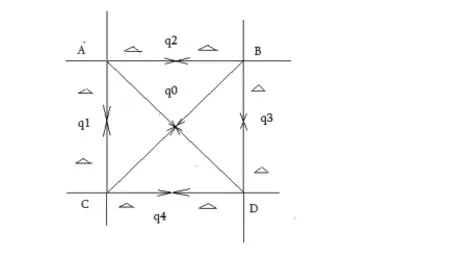
图1
3. 举例
为了更好地理解这种方法,下面举几个简单而有特性的例子。
3.1 正方形带电导体
3.1.1 环境与条件:一张边长为b极薄的正方形带有Qs电量的导体,因不考虑厚度的影响。在没有任何电磁场干扰的理想情况下计算电荷分布概率。
3.1.2 阐述:将正方形带有电荷导体分割为n=3,m=3,边长为2△的9个小正方形。如图2,其中Q11、Q12、Q13、Q21、Q22、Q23、Q31、Q32、Q33为中心电荷点,q11、q12、q21、q22、q31、q32为水平测试点,q011、q012、q021、q022、q031、q032为垂直测试点。

其水平分量为:

以此类推。
3.1.3 图例

图2
3.1.4 根据图示和运算方法建立数学模型:

3.1.5 运算结果:约去△、K、q,解得:

3.2 异形平面带电体之一:
3.2.1 环境与条件:一张边长为b极薄的十字形带有Qs电量的导体,因不考虑厚度的影响。在没有任何电磁场干扰的理想情况下计算电荷分布概率。
3.2.2 阐述:如图3,将其分割为5个边长2△正方形,建立中心电荷点Q12、Q21、Q22、Q23、Q32;q21、q22为水平方向测试点q021、q022为垂直方向测试点。
3.2.3 图例

图3
3.2.4 根据图示和运算方法建立数学模型:

3.2.5 运算结果:约去△、K、q,解得:
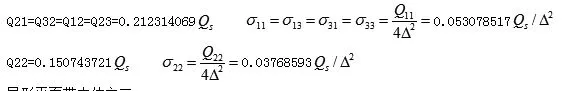
异形平面带电体之二:
3.2.6 环境与条件:一张如图4极薄的异形带有Qs电量的导体,因不考虑厚度的影响。在没有任何电磁场干扰的理想情况下计算电荷分布概率。
3.2.7 阐述:如图4,将其分割为6个边长2△正方形,建立中心电荷点Q11、Q12、Q22、Q23、Q31、Q32;q11、q31、q22为水平方向测试点q021、q022为垂直方向测试点。
3.2.8 图例:

图4
3.2.9 根据图示和运算方法建立数学模型:

3.2.10 运算结果:约去△、K、q

3.3 平行带状带电体:
3.3.1 环境与条件:有一条宽度为b长度很长的带状带电平面导体,因不考虑厚度的影响。在没有任何电磁场干扰的理想情况下,为了便于计算在带状导体轴向上只取2△长度中存储电荷量Qs0来加以计算,进行密度的相对比较。
3.3.2 阐述:如图5,从上一篇论文中可知非常大平面导体其中部电荷密度值是一样的,因此可以认为在很长的带状导体中轴向方向每条平行线上电荷密度是一致的。而径向长度只有b长,所以径向电荷会有很大的变化。在此将带状带电平面导体将其分割为n=5条宽2△带状,建立5个中心电荷点Q1、Q2、Q3、Q4、Q5;4个测试点q1、q2、q3、q4,l为测试点到中心电荷带的距离,A为测试点到电荷点dQi的距离,σQi为中心电荷带的密度。
由于轴向电荷密度一致,将中心电荷点改用中心电荷带,采用积分的方法将带上各个电荷点对测试点的电场径向作用力进行积分并令其各个为静态可求得电荷分布概率。
对于中心电荷带上每个电荷点σQi2△dt(i=1、2、3、4、5)对测试点q的径向作用力为:

3.3.3 图例:

图5
3.3.4 根据图示和运算方法建立数学模型:

3.4 平面圆导体:
3.4.1 环境与条件:有一个直径为b的圆形平面带电导体,因不考虑厚度的影响。在没有任何电磁场干扰的理想情况下,加以计算进行密度的相对比较.
3.4.2 阐述:在平面图形完全对称圆形带电导体,是一种特殊的形状,具有特殊性能,并且经常应用到,所以在此重点阐述。
在平面圆静态导体中任取一点A,在过A点直径的切线方向上电场力为零时,必然存在这么一种情况,有无数个相对于此直径的对称点,其对称点中的电荷密度必相等。在此条件下必然存在切线方向的静态平衡。而当某一趋近于此直径的对称点如B、C两点若Qb点要等于Qc则σb必等于σc。(导体为连续的电荷分布也是连续的)由于对称的圆形,直径与B、C两点可存而在于360度任何地方,所以同半径的圆环中的电荷密度是相等。也同时证明此直径的所有对称点的电荷密度也是分别相等的。而直径方向可以通过计算求得环形电荷密度的变化梯度。由于环状分布直径上分布概率应是以中心为对称的,这与线性导体电荷分布相吻合。
为了简单化将直径为b的圆分割为3个环形区域分别为σ1、σ2、σ3每环宽度2△。为了符合分割的3个注意事项做了如图的分割,由于对称只画出一个象限。Q1、Q2、Q3、Q4、Q5、Q6为直径上中心电荷点,位于每环与直径相交线的中间。Q4’、Q4”、Q5’、Q01、Q02为各分割面积中心电荷点。Q4’、Q4”、Q5’位于Q5、Q6半径环与Q4、Q5切线交叉点。Q01、Q02位于其分割面积中离一个直角边的距离是另一个直角边长的1/3。q1、q2、q3、q4、q5为直径线的测试点,方向为径向,位于直径方向上中心电荷点之中间。
设定:GH=PQ=2×1.67;b=12△通过设定和图形可计算出各种参数,将其代入数学模型。
3.4.3 图例:

图6
3.4.4 根据图示和运算方法建立数学模型:

4. 结束语
经过上面的探索和计算可以看出电荷即不是均匀分布在导体内,也不是停留在导体的表面,而是由中心向外逐渐递增,而且分割的越细计算的越精准递增的值就越大。
[1]迪派克(Dipak,L.S)唯迪斯(Valdis,V.L)著;沈远茂等译.应用电磁学与电磁兼容[M].北京:机械工业出版社,2009.
[2]汪泉弟,张淮清.电磁场[M].北京:科学出版社,2013.
[3]张洪欣,沈远茂,韩宇南.电磁场与电磁波[M].北京:清华大学出版社,2013.
[4]付云起,张光甫,莫锦军,吴微微.天线理论与工程[M].北京:电子工业出版社,2015.
徐卫星(1957-),男,浙江金华人,学士学位,高级工程师, 主要研究方向:电气测量。
