基于流-固耦合舰船地震波数值模拟研究
2017-09-14沈阳理工大学装备工程学院张自圃
沈阳理工大学装备工程学院 任 波 吴 强 张自圃
基于流-固耦合舰船地震波数值模拟研究
沈阳理工大学装备工程学院 任 波 吴 强 张自圃
航行舰船的低频噪声在海底基岩中引起振动,产生弹性波,并向远处传播,该波即为舰船地震波。采用有限元软件ANSYS/LSDYNA中的流-固耦合方法,建立了简单海洋环境的数值模型。利用该模型,对低频点声源引起的海底地震波进行了数值模拟。通过仿真计算,得到了流-固界面处的水平速度和垂直速度的波形曲线,通过和实验数据对比表明:数值计算结果和实验数据的波形曲线基本一致,从而证明了数值计算结果的可行性。并对数值计算的结果进行了分析计算,得到了Scholte表面波的特性及传播规律。
点声源;地震波;ANSYS/LS-DYNA;流-固耦合
航行舰船引起的振动、噪声和水体扰动在流体介质中形成压力波,压力波经由流体介质传播到海底,引起海底介质的振动,以弹性波的形式在海底界面和海底传播,这种波即为舰船海底地震波。水雷引信常用的物理场是舰船的声场、磁场和水压场,但随着消声降噪、消磁等措施的不断完善,使上述物理场在水中引起的场变化减弱,传统水雷引信对舰船的探测难度增加[1]。因此,需要开发研究新的物理场引信。目前,舰船海底地震波已经在美、俄水雷的引信中得到应用,并开发出了地震波引信水雷的系列产品[2]。因为海底地震波的频率成分极低,海底地震波比体波振幅大,衰减慢,传播距离远,弥补了传统引信的不足,很适合水中目标的探测。
本文主要针对典型的三维半无限空间层状海洋环境,采用有限元软件ANSYS/LS-DYNA,对简单水平分层海洋环境[3],海底地震波进行了数值模拟。分析了在基岩介质下,海底地震波在流-固界面产生的Scholte波的特性和传播规律。
1 数值计算方法
有限元软件ANSYS/LS-DYNA提供了流-固耦合方法[4],因而可用于计算流体-固体结构之间的相互作用。可用于低频点声源海底地震波的数值模拟[5]。固体、流体的有限元控制方程为:

式中:Ms、Cs、Ks分别为固体结构的质量矩阵、阻尼矩阵和刚度矩阵;Mf、Cf、Kf分别为流体介质的质量矩阵、阻尼矩阵和刚度矩阵;U、P分别为有限元节点的位移和声压[6];Fs、Ff分别为施加在固体结构上的外力和作用在流体介质上的压力;R为耦合矩阵,代表与流体-固体结构界面上节点相联系的有效表面积[7]。把Fs、Ff放在方程的右边,其他未知节点的唯一和声压放在左边,将上面两个方程合并为一个方程[5],即可得到流-固耦合问题的有限元离散方程,形式如下:
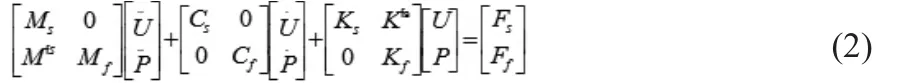
2 数值计算模型
2.1 舰船地震波仿真分析的方法
与其他有限元分析方法一样,舰船地震波仿真分析的步骤也包括前处理(建立有限元模型)、求解和后处理。
2.2 点声源的选择及有限元模型
考虑到声源的特殊性和复杂性,本文采用雷克子波模拟脉冲式点震源,可以简单地理解为围绕一个固定的频率左右包含了一定频率范围的脉冲信号。雷克子波是地震子波的一种。其表达式为:

其中:B为负值;f 为频率;t0为时移。
图1分别为本文所采用的主频为10HZ的低频雷克子波的时域图和频谱图。
本文采用2m×2m的正方形表面模拟点声源,位于模型顶部平面上。图2为点声源的局部网格。
2.3 有限元模型的建立
由于低频点声源海底地震波模型的对称性,简单起见,建立1/4模型。计算模型长、宽高分别为500m、500m和100m。海水密度为1000kg/m3,波速1500m/s,海底基岩密度2650kg/m3,纵波波速3098m/s,横波波速1789m/s,水深40m,海底基岩深60m。
本文建立的数值计算模型和网格划分如图3所示。上部分为海水,下部为海底基岩,海水(流体)与海底基岩(固体)界面为流-固接触面FSI。图2中顶面为自由液面,计算模型的左面和前面为对称界面(xOy面和yOz面)。真实的海洋环境下,其水平方向和竖直方向是无限大的,但是数值计算模型不可能无限大,可通过在边界面上施加无反射边界条件,从而将原来的无限域截断为有限的波动计算域。在文中的计算模型中,模型的右面、背面和底面都施加了无反射边界条件。
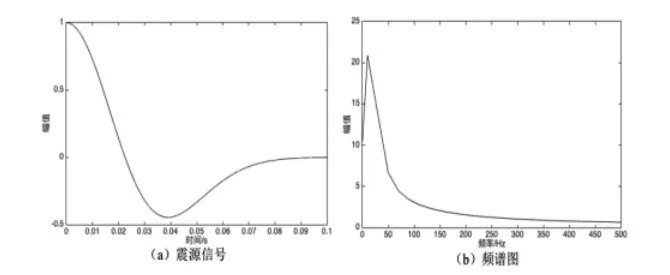
图1 点声源信号的时域图和频谱图

图3 数值计算模型和网格划分
3 结果及分析
3.1 海底地震波的传播特性
文献[6]指出航行舰船产生的在海底传播的次声场的传播形式为Scholte波[8]。舰船辐射噪声和海底交互作用产生的地震波类型如图4所示:
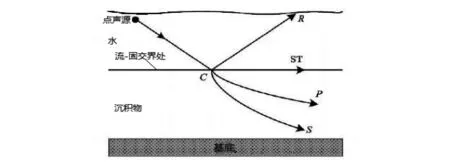
图4 波的类型
图中R为海底反射波;P为纵波;S为横波;ST为表面切变波Scholte波;并且沿着流-固表面传播。
以下为本文仿真图:
图5为在点声源作用下波的产生及传播到海底基岩的波形图。在29ms时,由点声源作用产生的压力波开始接触海底基岩。

图5 波的产生及传播到海底基岩的波形图
图6为波在流-固界面处的传播。由图7可以看出,在点声源作用下产生的压力波经海水介质传播到海底基岩介质,并在流体-固体交界面上传播,并且由于波的传播速度不同,可以明显的看出三个波(纵波、横波以及Scholte波)的阵列,且纵波传播速度最快,横波次之,Scholte波传播速度最慢,在流-固交界面产生并向远处传播。

图6 波在流-固界面处的传播
3.2 Scholte波传播特性研究
1978年,Dieter Rauch利用由三个正交的水听器和一个水听器组成的海底地震波拾振器进行了爆炸声的海底地震波接收的海上实验,实验得到了地震波的时间/距离信号(图7)、Scholte波质点运动轨迹(图8)。
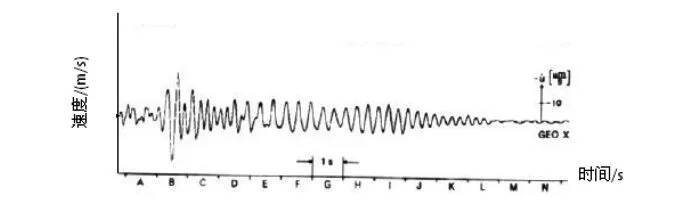
图7 水平方向地震波时域波形
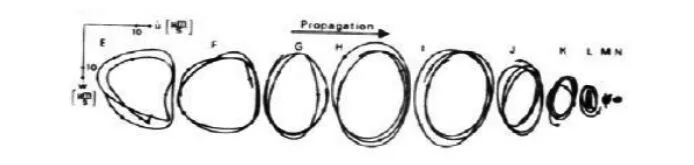
图8 Scholte波质点运动轨迹
为了验证本文仿真结果的正确性,取计算模型流-固交界面距离声源300m的节点的波形曲线,图9水平方向的波形曲线。

图9 水平方向的波形曲线
对图9中0.384s-0.466s以及0.384s-0.423s和0.423s-0.466s以及时间段内的波形轨迹进行极化,如图10所示。
通过对比图7、9的波形曲线,可以看出虽然波形和真实的地震波数据有所区别,但是波形曲线基本一致。通过对比图8、10,可以看出数值计算的质点运动轨迹和实验所得的质点运动轨迹都为逆进的椭圆,综上证明了数值计算结果的正确性。
为了进一步分析Scholte波的传播特性,分别取流-固交界面距离声源250m和300m处的节点垂直方向的波形曲线,如图11所示。

图10 质点运动轨迹

图11 250m和300m垂直方向的波形曲线
分别取图中1、2、3、4点的纵坐标值,如表1所示。

表1 不同距离处的幅值及衰减百分比
由图11和表1可以看出,横波和纵波衰减较快,Scholte波衰减比较慢。且随之距离的增加,Scholte波呈指数衰减。因而Scholte波比横波和纵波传播的远,可用于识别舰船目标。
4 结论
通过以上分析,本文首先证明了数值仿真结果的合理性和正确性,在此基础上,又进一部分析了Scholte波的特性及传播规律。
1)纵波和横波可以在岩层中传播,且纵波传播速度最快,横波传播速度次之,Scholte波传播速度最慢,在流-固交界面产生并向远处传播。
2)在流-固界面处,横波和纵波衰减快,Scholte衰减慢。且随之距离的增加,Scholte波呈指数衰减,因而Scholte波可以传播的很远,可用于识别舰船目标。
3)Scholte波沿着海底界面传播,质点运动轨迹为逆进的椭圆,
[1]孟路稳,程广利,陈亚男,等.舰船地震波传播机理及其在水雷引信中的应用研究[J].兵工学报,2017,38(2).
[2][3]卢再华,张志宏,顾建农.舰船海底地震波及其在水雷引信中的应用[J].水雷战与舰船防护,2004(4).
[4]陈云飞,吕俊军.航行舰船地震波及其在水中目标探测中的应用[J].舰船科学技术,2005,27(3).
[5]颜冰,周伟,龚沈光.浅海地震波传播的简正波模型[J].武汉理工大学学报,2006,30(5).
[6]Schmalfeldt B.Ambient and ship-induced low-frequency noise in shallow water[C]//Bottom-interacting ocean a-coustics.la Spezia,Italy,1980.
