2001—2014年中国植被净初级生产力时空变化及其与气象因素的关系

刘 刚,孙 睿,*,肖志强,崔天翔

1 北京师范大学地理学与遥感科学学院,北京 100875 2 北京师范大学/中国科学院遥感与数字地球研究所, 遥感科学国家重点实验室, 北京 100875

2001—2014年中国植被净初级生产力时空变化及其与气象因素的关系

刘 刚1,2,孙 睿1,2,*,肖志强1,2,崔天翔1,2

1 北京师范大学地理学与遥感科学学院,北京 100875 2 北京师范大学/中国科学院遥感与数字地球研究所, 遥感科学国家重点实验室, 北京 100875

植被净初级生产力(NPP)是表征植被活动的关键变量,对于评估生态系统承载力,理解陆地生态系统碳循环有着重要意义。以全球陆表特征数据集(GLASS)为基础,对2001—2014年中国植被NPP进行了估算。在此基础上,利用一元线性回归、经验正交分解(EOF)分析了我国植被NPP时空变化,利用逐象元相关性分析、奇异值分解(SVD)两种方法分析了我国植被NPP与温度、降雨量的相关性。结果表明：(1)我国植被NPP空间上基本呈由东南向西北递减的分布趋势,主要是由于植被分布和气候条件决定的。研究期间我国植被NPP呈波动增加趋势,总量在3.02—3.49PgC/a之间,平均约为3.25 PgC/a。(2)一元线性回归与EOF分析结果较为一致,表明我国长江中下游、华北平原和东北长白山地区NPP呈减少趋势,而青藏高原、西北、内蒙古中部及东南沿海地区NPP呈增加趋势。(3)NPP与气象要素逐象元相关性分析表明,长白山、青藏高原及南方地区NPP与温度呈正相关,内蒙东部和西北地区NPP与降雨量呈正相关,东北、长江下游地区NPP与降雨量呈负相关。SVD分析结果与逐象元分析结果基本一致表明,NPP与温度、降雨量均存在明显相关性,长白山、内蒙古、青藏高原地区NPP与温度正相关,西北、内蒙中部地区NPP与降雨量呈正相关,长江下游、东北地区NPP与降雨量呈负相关。

NPP；时空变化特征；气候因素；中国

工业革命以来,人们对于环境的过度干扰与破坏已经给整个生态系统造成了巨大的压力。大量化石燃料的燃烧使得大气中CO2等其他温室气体浓度增加,并触发了一系列环境问题,如全球温度升高、干旱问题加剧、植被地域分布改变等[1-2]。Zhao等在研究全球植被净第一性生产力变化过程中发现,年际NPP与大气中CO2浓度呈现明显负相关关系,表明NPP在降低大气CO2中扮演重要作用[3]。由此可见,NPP在调节全球气候变化,研究全球碳通量中扮演着重要角色[4- 6]。因此,国际生物圈计划(International Biology Plans,IBP)、世界气候研究计划(World Climate Research Programme,WCRP)、国际地圈-生物圈计划(International Geosphere-Biosphere Program,IGBP)等均将其作为核心研究内容[7]。

植被NPP的研究最早可追溯到19世纪80年代,在20世纪80年代取得了长足进步[8]。近年来,随着数据源的丰富和研究方法的改进,植被NPP研究进入新的发展阶段。目前,国内外学者对我国植被NPP进行了大量研究。孙睿等利用光能利用率模型估算了中国1992年4月至1993年3月的植被NPP,并认为水分条件是影响中国植被NPP的主要因素[9]。朱文泉等利用改进的光能利用率模型估算了中国1982至1999年植被NPP,并认为该段时间范围内降水、温度和光照均有利于植被的生长,胁迫较弱[10]。相同时间段内,朴世龙等[11]基于Carnegie-Ames-Stanford Approach(CASA)模型的研究结果表明,中国植被NPP呈增加趋势,并认为降水是主要限制因子。Liang等基于CASA模型估算了1982—2010年我国植被NPP时空变化并探讨了气候因素的影响机制[12]。Pei等估算了中国2001—2010年植被NPP,并分析了干旱对植被NPP的影响[1]。然而,不同研究结果之间一致性较低,模拟结果在1.43—6.13PgC之间[13]。同时由于数据源和方法的限制,大尺度NPP研究一般空间分辨率较低,在一定程度上影响了模拟精度。时空变化及影响因素分析主要局限于定性描述、一元线性回归和简单相关性分析等方法,分析方法较为单一。

本文基于Cui等[14,15]所开发的NPP产品生产算法,利用GLASS遥感数据集空间分辨率较高、时间跨度长、空间连续性好的特点,估算了2001—2014年空间分辨率为0.01°的中国植被NPP。利用多种方法分析了NPP时空变化及其对气象要素响应机制。为评价植被生产力对人类活动、气候变化的响应及制定生态环境治理政策提供依据。

1 数据来源和数据预处理

植被NPP模型输入数据包括：叶面积指数(LAI)、光合有效辐射吸收比例(FPAR)、植被覆盖度(FVC)、土地利用分类数据、森林生物量数据、气象数据以及高程数据等。

1.1 LAI、FPAR和FVC数据

研究所用2001—2014年LAI数据来自于北京师范大学生产的GLASS-LAI数据集[16],FPAR和FVC数据是由GLASS-LAI数据结合植被冠层辐射传输模型计算得到[17-18]。GLASS数据集是目前全世界时间跨度最长的全球地表特征产品之一。针对不同区域不同植被类型,对GLASS产品进行广泛的验证结果表明,GLASS产品空间上完整,时间上平滑连续,产品精度较高。数据空间分辨率为1km,时间步长为8d,投影方式为正弦曲线投影。本研究以C++为平台进行批量拼接、投影转换和裁剪,从而节省计算时间。

1.2 土地利用分类数据

土地利用分类数据来自于国家基础地理中心生产的2010年全球30米分类数据[19],该数据是全球首套30m分辨率地表覆盖数据,具有空间分辨率高、分类精度高等特点。本研究通过众数采样法将其重采样为0.01°空间分辨率。该数据包括耕地、混交林、阔叶林、针叶林、草地、灌木、湿地、水域、人造覆盖、裸地以及永久冰雪共11种地类。但缺少对阔叶林、针叶林和灌丛是常绿或落叶、稀疏或郁闭的细分,因而本研究以GLASS冬季LAI数据为基础对,通过自然间断点分割法分别对3种地类进行划分,阈值分别为0.95、0.50和0.25。

1.3 生物量数据

植被生物量是估算植被自养呼吸的重要参数。本研究将植被分为非林地和林地两类。非林地植被生物量通过LAI和比叶面积(Specific Leaf Area,SLA)计算。林地植被以我国第七次森林清查数据为基础,利用罗云建所研究的森林蓄积量-生物量转换公式进行计算[20]。具体地,假定每个栅格格点分布一棵致密程度各异的大树,该树高度由GLAS冠高数据(http://webmap.ornl.gov/wcsdown/dataset.jsp?ds_id=10023)表征,致密程度由据植被覆盖产品MOD44B (https://ladsweb.nascom.nasa.gov/data/search.html)表征。参考曾伟生等全国立木生物量建模总体划分方案,将全国划分为六大地理区域[21](西北、西藏、西南、南方、华北、东北),并收集各区域代表树种立木生物量研究结果,从而建立模型所得全国森林生物量分布图。以该计算结果为纽带,建立空间格点生物量和该省该类森林生物量均值之间的转换关系(式1)。从而通过降尺度分配得到每个栅格象元的生物量。

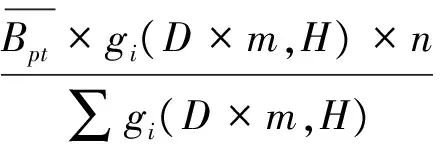
(1)

1.4 气象数据

气象驱动数据为全球陆地数据同化系统(Global Land Data Assimilation System,GLDAS)(http://ldas.gsfc.nasa.gov/gldas/GLDASgoals.php)数据集。主要包括气温、向下短波辐射、向下短波净辐射、长波净辐射和比湿数据集五个子数据集。数据空间分辨率为0.25°,时间步长为3h。温度和比湿数据预处理是将8d数据累加求平均,从而得到平均温度和平均比湿。向下短波辐射数据处理时,通过累加得到8d的总辐射(MJ/m2),然后乘系数0.5,将向下短波辐射转换成光合有效辐射。向下短波净辐射和长波净辐射的处理方法与向下短波辐射相同。最后通过双线性法将各数据集重采样到0.01°空间分辨率,其中温度插值时利用气温直减率进行了高度校正。2001—2012年降雨量数据由中国气象局提供,分辨率为0.0625°,主要用于分析降雨量对植被NPP的影响。

2 研究方法

2.1 植被NPP模型

植被NPP估算模型MuSyQ-NPP (Multi-source data Synergized Quantitative remote sensing production system-Net Primary Productivity),将GPP的形成与自养呼吸过程看作两个相对独立的过程[15]。其中,GPP通过光能利用率模型来进行计算,主要取决于植被吸收的光合有效辐射和光能利用率。NPP为GPP中扣除自养呼吸的部分:

GPP=εg·FPAR·PAR·f1(T)·f2(β)

(2)

NPP=GPP-Ra

(3)

式中,εg为最大光能利用率,本研究εg取值参考MODIS NPP算法取值[3,15]。PAR为光合有效辐射。FPAR为植物吸收的光合有效辐射比例,是植被冠层吸收的PAR占入射PAR的比例,与植被自身的生长状况有关。f1(T)为温度胁迫因子,其计算参考CASA模型计算公式[22]。f2(β)为水分胁迫因子,通过地表实际蒸散量与潜在蒸散量的比值求得。其中实际蒸散量采用Penman-Monteith公式,结合LAI、FVC及比湿数据进行计算。潜在蒸散采用Priestley-Taylor方程计算[15]。Ra为自养呼吸：

Ra=Rm+Rg=∑Rm,i+Rg

(4)

Rm,i=Mirm,iQ10,i(T-Tb)/10

(5)

Rg=γ(GPP-Rm)

(6)

式中,Rm为维持呼吸,Rg为生长呼吸。i代表植被的不同部分,包括根、茎、叶。Mi为植被i部分参与呼吸的生物量,rm,i为植被第i部分的维持呼吸系数,Q10,i为植被i部分温度敏感因子,Tb为基温,T为平均温度。生长呼吸与温度无关,与总初级生产力成一定的比例关系,为生长呼吸系数。

2.2 时空变化与影响因素分析方法

首先,本文选择逐象元一元线性回归和EOF分析两种方法分析中国植被NPP时空变化趋势。第二,引入降雨量和年均温两个气象因子,通过逐象元相关性分析和SVD分析两种方法分析NPP对气象因素的响应机制。

EOF是分析要素场时空变化的重要工具[23]。运用EOF分解可以将长时间序列大空间尺度的要素场分解为空间典型场和时间系数,进而反映要素的空间特性及其随时间的变化。EOF分解得到的多个模态之间空间上相互正交,且收敛快,前几个模态即可反应原始数据大部分时空变化规律。算法以研究区中变量X的n次观测值为基础构造矩阵Xm×n,并对其进行标准化处理。根据矩阵Xm×n构造相关系数矩阵Cm×m,并对其进行对角化运算(式7):

C=X·XT=(V·T)·(V·T)T=V·Λ·VT?

(7)

式中,V是EOF输入变量对应的特征向量,Λ是特征值对角矩阵,可根据Λ计算模态的贡献率。由V计算得到时间系数T(式8),进而将Xm×n分解为空间模态和时间系数的乘积之和(式9):

T=VT·X

(8)

X=V·T

(9)

SVD分析是提取两个要素场耦合信号的重要工具[24]。最早主要用于气象要素场分析,近年来被引入到地学领域。SVD分析以两个场的交叉协方差矩阵展开(式10),并对其进行广义对角化运算(式11),得到奇异值和左右场:

C=F·GT

(10)

C=U·Λ·VT

(11)

式中,C是交叉协方差矩阵,F和G分别是两个要素场,U和V中的向量是矩阵C的奇异向量,Λ是对角矩阵,对角线上的元素是奇异值,根据奇异值可以计算每一对奇异向量所代表空间模态的协方差贡献率(Squared Covariance Fraction,SCF)和累积协方差贡献率(Cumulative Squared Covariance Fraction,CSCF)。在此基础上可计算左右场的时间系数(式12,式13):

Tf=UT·F

(12)

Tg=VT·G

(13)

式中,Tf和Tg分别为左右奇异向量的时间系数。时间系数的相关性越大表明两个场的相关性越高。定义左场时间系数与右场时间系数为模态时间系数,表示第n对模态之间的相关度。定义左(右)场时间系数与左(右)场序列之间的时间相关系数为同性相关系数,表示一个场与其时间系数之间的相关分布。左(右)场时间系数与右(左)场序列之间的时间相关系数为异性相关系数,表示一个场的时间系数与另一个场的相关分布。在一对异性相关型中,当区域内左右场变化趋势一致(均为高值或低值)则表明两个场呈正相关,反之则呈负相关。显著相关区表示两个场相互影响的关键区,由此可确定左右场的遥相关型。本文分析中主要考虑异性相关系数。

3 研究结果与分析

3.1 NPP估算结果

2001—2014年NPP年均值分布(图1)来看,我国植被NPP基本呈现由东南向西北递减的分布趋势,与前人研究结果基本一致。其中,南方地区年平均NPP最高,超过700gC m-2a-1,主要原因是这些地区水热条件较好,森林植被占有很大比例,植被覆盖度较高。西北地区年平均NPP较低,小于130gC m-2a-1,主要是由于该地区主要以荒漠和草地为主,植被生长受降水限制；东北和华北NPP均值则主要在300—700gC m-2a-1之间。

从植被NPP年际变化来看(图2),近14年我国受气候影响NPP波动较大。研究期间我国植被NPP呈现波动增加趋势,增长率为0.01 PgC/a。植被NPP年总量在3.02—3.49PgC之间,均值约为3.25PgC。其中峰值出现在2004、2007和2013年,其中2013年最高为3.49PgC。低值出现在2003、2005和2009年,其中2009年最低为3.02 PgC。近年来,我国受极端天气和气候变化的影响,NPP波动较大。2003、2005年出现低值的可能原因是气象灾害,该年份南方降水偏少,同时夏季出现罕见干旱。2009年出现最低值则可能是由于2008年底的雪灾及夏季的干旱导致的。2004、2007和2013年水热条件较为适宜,因而出现高值。

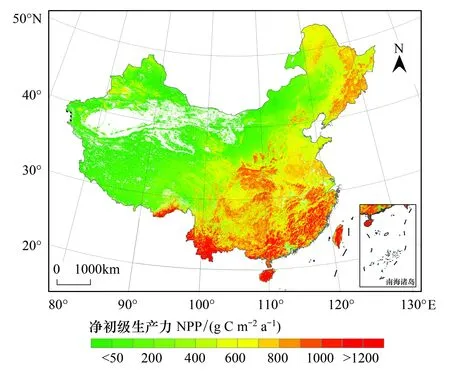
图1 中国NPP空间分布Fig.1 Spatial distribution of mean NPP in China in 2001—2014

图2 中国植被NPP年际变化Fig.2 Interannual variations of total NPP in China from 2001 to 2014

同类研究中,由于模型机理、参数及数据源的不同,模型模拟结果也有所差异。本文NPP估算结果与前人研究结果对比如表1所示。从量级上来看,本研究估算结果在同类研究区间范围内,低于陈斌、陈福军等人的研究结果,高于Pei和高志强等人的研究结果。从变化趋势上来看,本研究与前人研究也表现出一致性,呈波动上升趋势,如Liang等[11]人在研究近30年中国植被NPP时空变化中发现,在2000—2010年期间,中国植被NPP的增长率为0.008 PgC/a；陈福军等[23]人研究1981—2008年中国植被NPP发现2003年出现低值；Liu等[2]人在研究2001—2010年中国植被NPP中发现,由于受极端天气影响2009年中国植被NPP出现最低值,均与本研究结果基本一致。

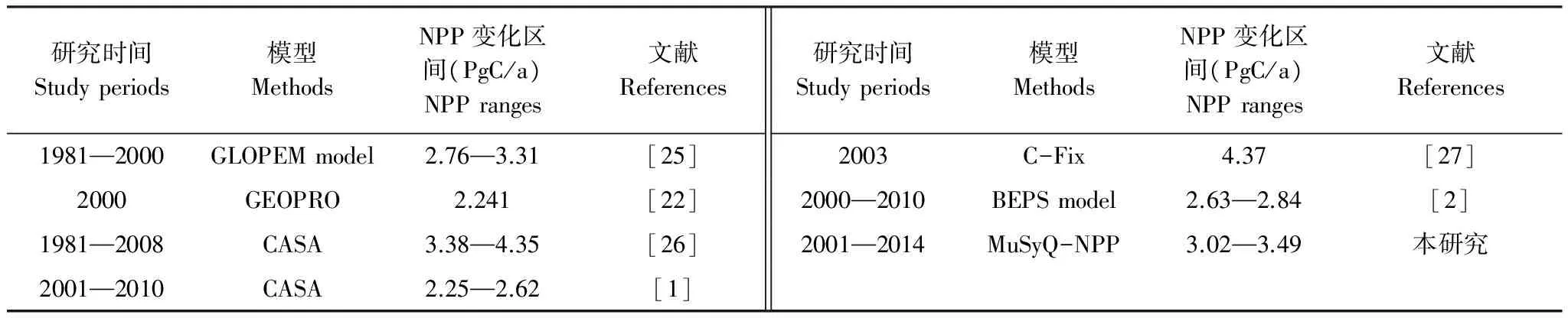
表1 同类研究结果对比

3.2 NPP时空变化

一元线性回归是对近14年年NPP值与年份进行线性回归,结果为NPP变化斜率,大于0则表示NPP增加,反之则为减少,拟合结果如图3所示。研究期间,59.72%的区域NPP有所增加,40.28%的区域NPP有所减少。其中,21.35%的区域植被NPP显著增加(P<0.05),增加区域主要分布在青藏高原、西北、内蒙古中部及东南沿海地区；10.51%的区域植被NPP显著减少(P<0.05),减少区域主要分布在长白山、华北平原和长江中游地区。

EOF分析的前5个特征向量的方差贡献率分别为24.68%、13.76%、10.89%、10.09%和7.84%,累积方差贡献率达到67.26%。本文主要分析第一特征向量的空间分布及其时间系数。从空间上来看(图4),高值区主要分布在青藏高原、西北、内蒙中部、山西北部及东北大兴安岭等地区。长江中下游、华北平原、中部和东北长白山地区NPP呈下降趋势,与Liu等人的研究结论基本一致[2]。主要原因是浙江、福建、广东等沿海地区已经进入工业化后期,生态环境得到修复,植被NPP有所增加。黄土高原、西北及东北地区植被NPP呈增加趋势,表明该区域生态修复工程作用显著。华北农业区及长江中下游地区主要以农业生态系统为主,生态环境较为脆弱,近年来频发的气象灾害是造成该区域NPP减少的主要原因。从该模态对应的时间系数(图略)来看,基本呈现增加趋势,与NPP年际变化趋势有所差异。主要原因是进行EOF分析的原数据经纬度范围为(15.85—54.50N,69.13—135.73E)的矩形,与中国行政边界有所差异,因而统计所得时间变化趋势与图2有所区别,下文奇异值分析所得时间系数同理。

图3 基于一元线性回归的NPP时空变化Fig.3 NPP trends based on linear regression

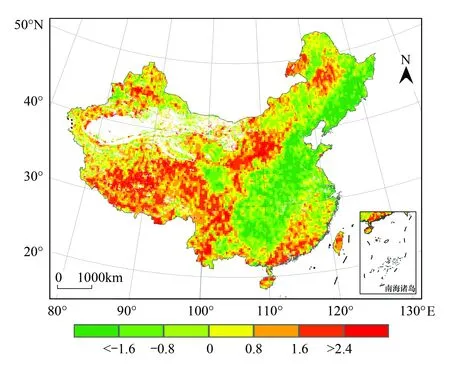
图4 EOF分析第一特征向量空间分布Fig.4 The spatial pattern of EOF1 for NPP in China

3.3 气象因素对NPP的影响

图5 逐象元NPP与年均温相关性分布 Fig.5 Correlation coefficients between annual NPP and air temperature

温度和降水是影响NPP的主要气象因子。本文选择逐象元相关性分析和SVD分析两种方法分析气象要素对植被NPP的影响。在SVD分析中,为减少计算量,通过双线性插值法将NPP和气象要素重采样到0.25°分辨率,并对NPP和气象要素(温度或降水)进行标准化处理。研究以NPP为左场、以气象要素为右场,对其交叉协方差矩阵进行奇异值分解,进而提取方差贡献率、时间相关系数、异性相关性及时间系数等信息。

3.3.1 温度对NPP的影响

基于逐象元的NPP与年均温相关性如图5所示。总体而言,NPP与年均温之间正、负相关并存,以正相关为主,主要分布在长白山、青藏高原以及南方地区,负相关区零星分布在内蒙古东部地区。总体而言,通过显著性检验的象元相对较少,通过P<0.01、P<0.05和P<0. 10置信区间的象元比例分别为4.72%、13.13%和20.23%。

NPP与年均温奇异值分解结果如表2所示。前三个模态的累积协方差贡献率达到83.70%,其中第一模态的累积协方差贡献率达到52.03%,对第一对模态进行分析即可揭示NPP与年均温之间的关系。前三对模态的时间相关系数分别为0.96、0.97、0.96,均通过了显著性检验(R0.01=0.66),表明NPP与年均温之间存在明显相关性。

表2 NPP与温度SVD分析结果

从NPP异性相关系数分布(图6)来看,第一模态正值区主要位于青藏高原、内蒙中部,最高值达到0.8。负值区主要华北和长白山地区,相关系数最高达到-0.8,其他区域相关性较低。从年均温异性相关系数分布(图7)来看,正值区主要位于西北、青藏高原及内蒙古中西部地区,最高达到0.85以上,负值区主要位于东北和长江下游地区,最低达到-0.7。这对空间分布型表明：当长白山、内蒙古中部、青藏高原地区温度增加(减少)时,NPP随之增加(减少),与逐象元相关性分析结果基本一致。主要原因是由于,长白山、内蒙古等地区温度较低,温度的增加有利于植被生长,而青藏高原海拔较高,植被蒸腾耗水量较少,植被生长主要受温度限制。从时间序列演变曲线(图8)来看,NPP与温度的变化趋势基本一致,但年均温变化幅度略大于NPP,表明NPP对于温度的响应存在一定滞后。

3.3.2 降雨量对NPP的影响

基于象元的NPP与降雨量进行相关性分布结果如图9所示。正相关区域主要分部在内蒙古东部和西北部分地区,负相关区域零星分布在东北、长江下游、青藏高原南部等地区。通过P<0.01、P<0.05和P<0.10置信区间的象元比例分别6.72%、15.21%和21.68%,通过显著性检验的象元比例较少。

将NPP与降雨量的交叉协方差矩阵进行奇异值分解,结果如表3所示。前3对模态累积协方差贡献率达到83.45%,可代表两个要素场的主要信息。前三对模态的时间相关系数均在0.90以上,通过了显著性检验(R0.01=0.62)。

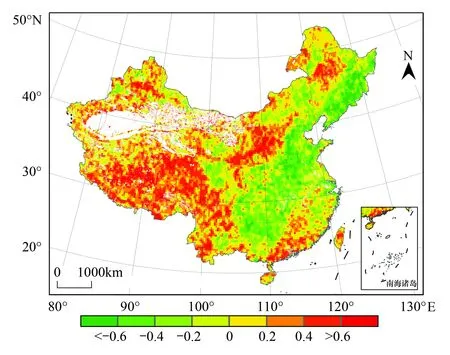
图6 第一模态NPP异性相关性分布Fig.6 Heterogenerous correlation patterns for the first mode of NPP

图7 第一模态年均温异性相关性分布Fig.7 Heterogenerous correlation patterns for the first mode of air temperature

图8 NPP与温度时间系数Fig.8 Time coefficients of NPP and air temperature

图9 NPP与降雨量相关性分布Fig.9 Correlation coefficients between NPP and precipitation

模态序号Mode方差贡献率/%Variancecontribution累积方差贡献率/%Cumulativevariance相关系数Correlationcoefficients141．4641．460．95214．6056．060．92311．7967．850．94

第一对模态解释了总方差的41.46%,通过对其分析可以阐述降水对NPP的影响。从NPP异性相关性分布(图10)来看,高值区主要分布在内蒙中东部和西北地区,低值区主要分布在华北、南方和长白山等地区。从降雨量异性相关性分布(图11)来看,高值区主要分布在长江中下游、西北、东北和内蒙古中东部等地区,低值区主要分布在云南地区。这对分布型表明：当长江中下游和东北地区降水增加(减少)时,NPP随之减少(增加)。西北、内蒙中东部降水增加(减少)时,NPP随着增加(减少)。主要原因是长江中下游地区降水丰沛,当降水增加时会减少光合有效辐射,从而减少植被NPP。东北等冷湿地区主要限制因素是温度,夏季降水对其影响不显著,但当冬季降水增加时,往往伴随强低温出现,从而限制植被生长。西北、内蒙古中部气候相对干燥,降水是植被生长的主要限制因子。从时间系数来看(图12),该模态中降雨量和NPP的变化趋势较为一致,相关系数达到0.95,通过了P<0.01的显著性检验。

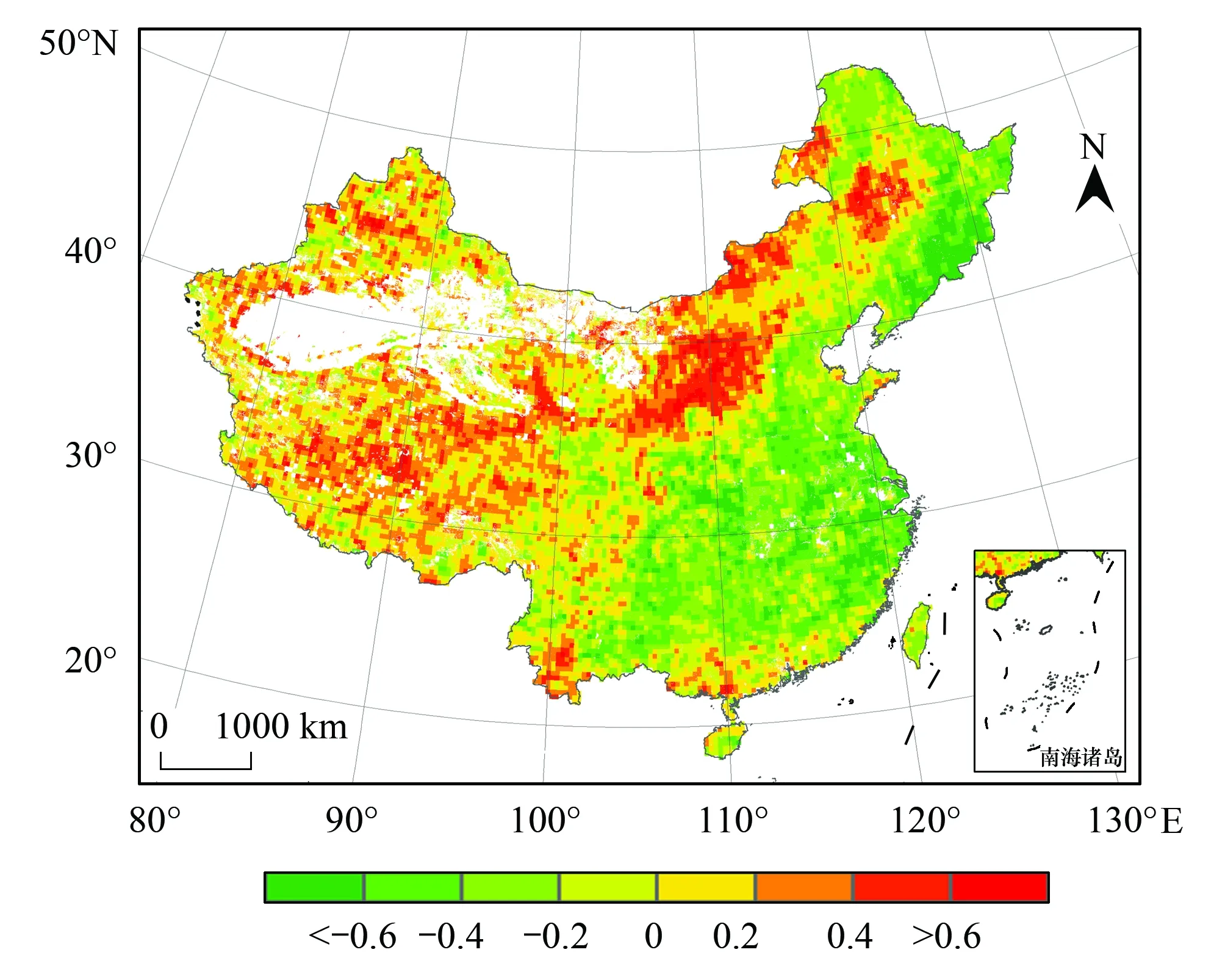
图10 第一模态NPP异性相关性分布Fig.10 Heterogenerous correlation patterns for the first mode of NPP

图11 第一模态降雨量异性相关性分布Fig.11 Heterogenerous correlation patterns for the first mode of precipitation

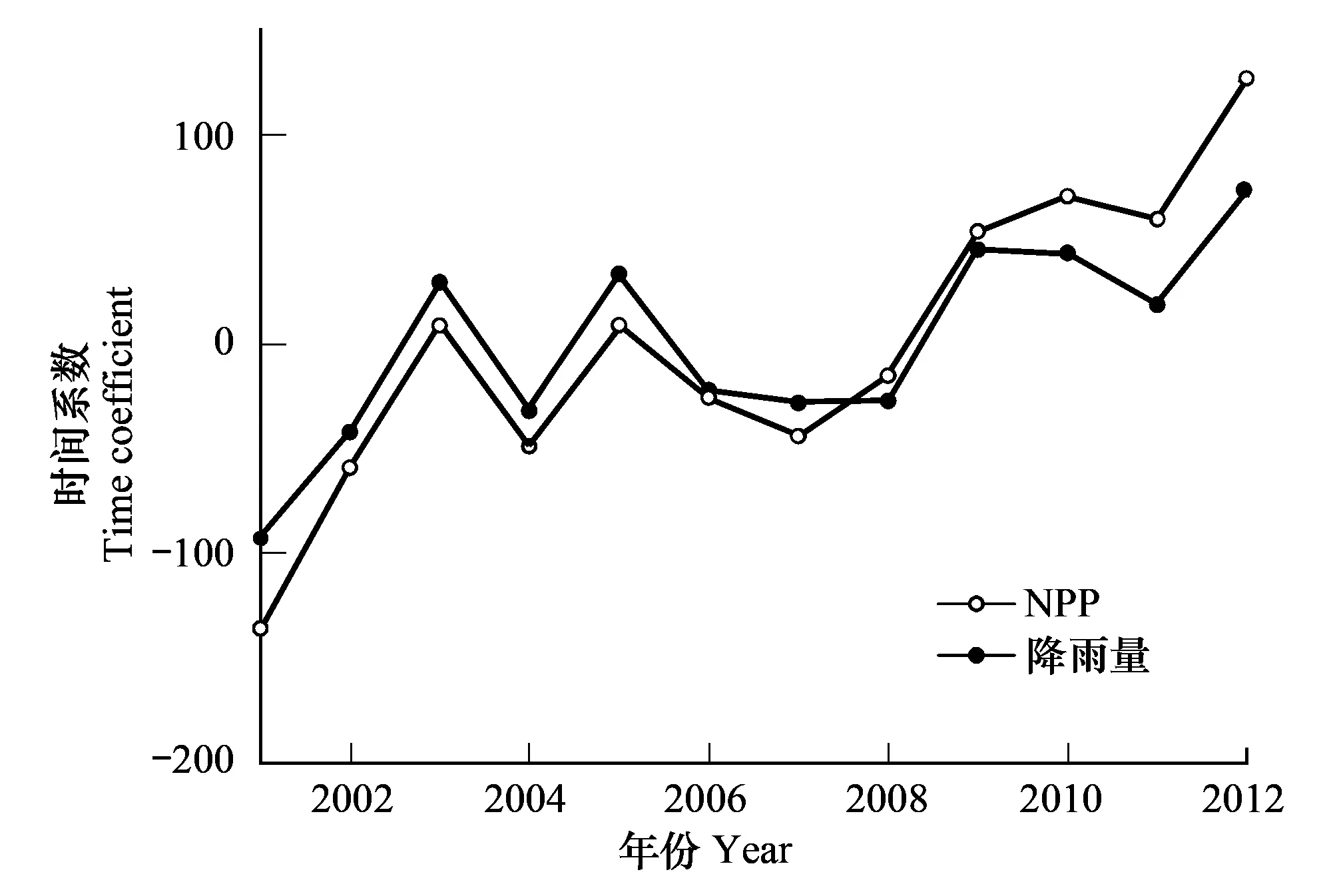
图12 NPP与降雨量时间系数 Fig.12 Time coefficients of NPP and precipitation

研究表明,对于相关性较为显著的区域,两种方法都能够较好地反映NPP与气象要素间的相互关系。由于样本量的限制相关性分析通过显著性检验的象元数量较少,从而表现出一定的局限性。SVD方法可以提取时间系数,从而可以从时间角度分析两个要素场的互动机制。

4 结论与讨论

本文基于MuSyQ-NPP模型估算了2001—2014年中国植被NPP。结果显示,研究期间我国植被NPP呈波动增加趋势,总量在3.02—3.49PgC/a之间,平均约为3.25 PgC/a。空间上基本呈由东南向西北递减的分布趋势,地区间变化分异明显。

一元线性回归和EOF分析所得结果较为一致,结果表明青藏高原、西北、内蒙古、山西北部及东北大兴安岭等地区植被NPP呈增加趋势,长江中下游、华北平原、中部和东北长白山地区植被NPP有所下降。传统逐象元相关性分析和SVD分析结果基本一致。结果表明：长白山地区、内蒙古及青藏高原地区NPP与年均温呈正相关。长江中下游和东北地区NPP与降雨量呈负相关,西北、内蒙古中部地区NPP与降雨量呈正相关。

比较而言,传统相关性分析在提取变量相关信息时存在一定局限性,这种局限性主要是由于变量的变化幅度和样本数量的限制,从而导致多数象元不能通过显著性检验。此外,传统的相关性分析无法解释变量之间是否存在因果关系,即变量周期性变化带来的假相关。SVD分析可以从场域的角度出发,分析区域内变量的互动关系。此外SVD分析可以通过提取时间系数分析变量之间的相互关系。然而该算法运算量较大,需要将原始数据重采样到较低分辨率,牺牲了一定的数据精度。

[1] Pei F S, Li X, Liu X P, Wang S J, He Z J. Assessing the differences in net primary productivity between pre- and post-urban land development in China. Agricultural and Forest Meteorology, 2013, 171-172: 174-186.

[2] Liu Y B, Ju W M, He H L, Wang S Q, Sun R, Zhang Y D. Changes of net primary productivity in China during recent 11 years detected using an ecological model driven by MODIS data. Frontiers of Earth Science, 2013, 7(1): 112-127.

[3] Zhao M S, Running S W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science, 2010, 329(5994): 940-943.

[4] Twine T E, Kucharik C J. Climate impacts on net primary productivity trends in natural and managed ecosystems of the central and eastern United States. Agricultural and Forest Meteorology, 2009, 149(12): 2143- 2161.

[5] 王李娟, 牛铮, 旷达. 基于MODIS数据的2002—2006年中国陆地NPP分析. 国土资源遥感, 2010, (4): 113- 116.

[6] 刘琳, 李月臣, 朱翠霞, 杨扬, 李琼瑶. 2001年—2010年重庆地区植被NPP时空变化特征及其与气候因子的关系. 遥感信息, 2013, 28(5): 99- 108.

[7] IGBP Terrestrial Carbon Working Group. The terrestrial carbon cycle: implications for the Kyoto Protocol. Science, 1998, 280(5368): 1393- 1394.

[8] 埃塞林顿 J R. 环境和植物生态学. 曲仲湘, 译. 北京: 科学出版社, 1989.

[9] 孙睿, 朱启疆. 中国陆地植被净第一性生产力及季节变化研究. 地理学报, 2000, 55(1): 36- 45.

[10] 朱文泉, 潘耀忠, 阳小琼, 宋国宝. 气候变化对中国陆地植被净初级生产力的影响分析. 科学通报, 2007, 52(21): 2535- 2541.

[11] 朴世龙, 方精云, 郭庆华. 1982—1999年我国植被净第一性生产力及其时空变化. 北京大学学报: 自然科学版, 2001, 37(4): 563- 569.

[12] Liang W, Yang Y T, Fan D M, Guan H D, Zhang T, Long D, Zhou Y, Bai D. Analysis of spatial and temporal patterns of net primary production and their climate controls in China from 1982 to 2010. Agricultural and Forest Meteorology, 2015, 204: 22- 36.

[13] 高燕妮, 于贵瑞, 张黎, 刘敏, 黄玫, 王秋凤. 中国陆地生态系统净初级生产力变化特征——基于过程模型和遥感模型的评估结果. 地理科学进展, 2012, 31(1): 109- 117.

[14] Zhang R H, Sun R, Du J P, Zhang T L, Tang Y, Xu H W, Yang S T, Jiang W G. Estimations of net primary productivity and evapotranspiration based on HJ- 1A/B data in Jinggangshan city, China. Journal of Mountain Science, 2013, 10(5): 777- 789.

[15] Cui T X, Wang Y J, Sun R, Qiao C, Fan W J, Jiang G Q, Hao L Y, Zhang L. Estimating vegetation primary production in the heihe river basin of china with multi-source and multi-scale data. PLoS One, 2016, 11(4): e153971.

[16] Xiao Z Q, Liang S L, Wang J D, Chen P, Yin X J, Zhang L Q, Song J L. Use of general regression neural networks for generating the GLASS leaf area index product from time-series MODIS surface reflectance. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 209- 223.

[17] Xiao Z Q, Liang S L, Sun R, Wang J D, Jiang B. Estimating the fraction of absorbed photosynthetically active radiation from the MODIS data based GLASS leaf area index product. Remote Sensing of Environment, 2015, 171: 105- 117.

[18] Xiao Z Q, Wang T T, Liang S L, Sun R. Estimating the fractional vegetation cover from GLASS leaf area index product. Remote Sensing, 2016, 8(4): 337.

[19] Chen J, Chen J, Liao A P, Cao X, Chen L J, Chen X H, He C Y, Han G, Peng S, Lu M, Zhang W W, Tong X H, Mills J. Global land cover mapping at 30m resolution: a POK-based operational approach. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 103: 7- 27.

[20] 罗云建, 王效科, 张小全, 逯非. 中国森林生态系统生物量及其分配研究. 北京: 中国林业出版社, 2013.

[21] 曾伟生. 全国立木生物量方程建模方法研究[D]. 北京: 中国林业科学研究院, 2011.

[22] Potter C S, Randerson J T, Field C B, Matson P A, Vitousek P M, Mooney H A, Klooster S A. Terrestrial ecosystem production: a process model based on global satellite and surface data. Global Biogeochemical Cycles, 1993, 7(4): 811- 841.

[23] 张雪珍. 1982—2011年北半球中纬度秋季植被绿度变化的主要模态. 地理科学, 2014, 34(10): 1226- 1232.

[24] 江志红, 丁裕国. 我国夏半年降水距平与北太平洋海温异常的奇异值分解法分析. 热带气象学报, 1995, 11(2): 133- 141.

[25] 高志强, 刘纪远. 中国植被净生产力的比较研究. 科学通报, 2008, 53(3): 317- 326.

[26] 陈福军, 沈彦俊, 李倩, 郭英, 徐丽梅. 中国陆地生态系统近30年NPP时空变化研究. 地理科学, 2011, 31(11): 1409- 1414.

[27] 陈斌, 王绍强, 刘荣高, 宋婷. 中国陆地生态系统NPP模拟及空间格局分析. 资源科学, 2007, 29(6): 45- 53.

AnalysisofspatialandtemporalvariationofnetprimaryproductivityandclimatecontrolsinChinafrom2001to2014

LIU Gang1,2,SUN Rui1,2,*,XIAO Zhiqiang1,2,CUI Tianxiang1,2

1SchoolofGeography,BeijingNormalUniversity,Beijing100875,China2StateKeyLaboratoryofRemoteSensingScience,JointlySponsoredbyBeijingNormalUniversityandtheInstituteofRemoteSensingandDigitalEarth,ChineseAcademyofSciences,Beijing100875,China

Net primary productivity (NPP) is a key variable in characterizing vegetation activity. NPP also plays an important role in evaluating ecosystem carrying capacity and understanding terrestrial ecosystem carbon cycle. The present study estimated the NPP in China from 2001 to 2014 based on the GLASS remote sensing dataset. We also analyzed the spatial and temporal variation of vegetation NPP in China with linear regression and Empirical Orthogonal Function (EOF) algorithms. By using correlation analysis and Singular Value Decomposition (SVD) method, the relationship between NPP and temperature and the relationship between NPP and precipitation were obtained, respectively. The results showed that (1) NPP in China revealed a decreasing pattern from southeast to northwest due to the spatial variability of vegetation and climatic characteristics. NPP also had a fluctuating increase trend during our study period with values ranging between 3.02 and 3.49 PgC/a. The average value was approximately 3.25 PgC/a. (2) The linear regression and EOF results are consistent. Both results indicated that NPP presented a decreasing tendency in the lower Yangtze region, North China Plain, and Changbai mountain area. In the Qinghai-Tibetan Plateau, northwest, central Inner Mongolia, and southeast coastal areas of China, NPP showed an increasing tendency. (3) The correlation analysis between NPP and meteorological elements indicated that NPP was positively correlated with temperature in the Changbai mountain area, Qinghai-Tibet Plateau, and southern area. NPP was also positively correlated with precipitation in the eastern Inner Mongolia and northwestern region. However, in the Northeast, Yangtze River, and east of the Qinghai-Tibetan Plateau area, NPP was negatively correlated with precipitation. The SVD results were consistent with the results of correlation analysis. We found significant correlations between NPP and temperature and precipitation. NPP was positively correlated with temperature in the Changbai mountain area, Inner Mongolia, and Qinghai-Tibet Plateau area. NPP was also positively correlated with precipitation in the northwest and central Inner Mongolia, whereas it was negatively correlated with precipitation in the lower Yangtze River and northeastern area.

NPP; spatial-temporal variation; climate controls; China

国家自然科学基金(41471349);国家科技支撑计划项目 (2013BAC03B02);中央高校基本科研业务费专项(2014kJJCA02)资助

2016- 04- 29; < class="emphasis_bold">网络出版日期

日期:2017- 03- 22

10.5846/stxb201604290822

*通讯作者Corresponding author.E-mail: sunrui@bnu.edu.cn

刘刚,孙睿,肖志强,崔天翔.2001—2014年中国植被净初级生产力时空变化及其与气象因素的关系.生态学报,2017,37(15):4936- 4945.

Liu G,Sun R,Xiao Z Q,Cui T X.Analysis of spatial and temporal variation of net primary productivity and climate controls in China from 2001 to 2014.Acta Ecologica Sinica,2017,37(15):4936- 4945.