地区生产总值与固定资产投资额的数据分析

2017-09-12吕林静

淮南职业技术学院学报 2017年4期

关键词：离群投资额线图

吕林静

(海南大学金融统计系，海口570228)

地区生产总值与固定资产投资额的数据分析

吕林静

(海南大学金融统计系，海口570228)

运用探索性数据分析的方法定量地分析各地全社会固定资产投资对于地区经济增长的拉动作用;分别运用最小二乘法和三组耐抗线的方法进行回归拟合，并且通过将原始残差进行不同尺度下的转换、对每个样本杠杆率进行计算以及残差箱线图判断异常值点，综合分析之后找出异常值，然后对去掉异常值点后的数据进行最小二乘法的回归，求出拟合直线，最后分别求出两种方法下的均方误差并对拟合模型的优劣进行评价。

地区生产总值； OLS；三组耐抗线；异常值

1 地区生产总值与固定资产投资概述

国内生产总值是指在一定时期内一个国家或地区的经济中所生产出的全部最终产品和劳务的价值，是衡量国家经济状况的最佳指标，不但可反映一个国家的经济表现，更可以反映一国的国力与财富。实际统计中，一般以支出法为标准来计算国内生产总值。在支出法中，投资支出直接构成了国内生产总值的一部分，而固定资产投资又是投资支出的重要组成部分。地区生产总值是指本地区所有常住单位在一定时期内生产活动的最终成果，是国内生产总值在不同地区的具体化。因此，研究地区生产总值与固定资产投资的关系是有必要的，本文主要对地区生产总值和固定资产投资总额的关系进行研究。

2 数据来源

为了定量地研究地区生产总值与固定资产投资额的关系，笔者选择了地区生产总值以及各地区全社会固定资产投资额作为研究对象，选取的样本为2014年中国 31 个省市的地区生产总值与全社会固定资产投资额。相关数据来源于统计局发行的《中国统计年鉴——2015》。其中，31个省市的生产总值在《中国统计年鉴——2015》“国民经济核算”下的 “地区生产总值和指数”中，全社会固定资产投资在《中国固定资产投资统计年鉴——2015》“固定资产投资”下的“各地区全社会固定资产投资”中。

3 地区生产总值与固定资产投资数据分析

为了便于分析，把各地区的地区生产总值记作Y，各地区全社会固定资产投资记作X。为了初步分析地区生产总值(Y)与全社会固定资产投资额(X)的关系，可以作出以X为横坐标，Y为纵坐标的散点图。通过对散点图的观察可以发现两者间存在着某种线性关系，于是假设地区生产总值与全社会固定资产投资额有着密切联系，下文进一步探讨与研究。

3.1 图形分析

通过绘制地区生产总值和全社会固定资产投资额这两个箱线图，如图1、图2所示。对比可得知，地区生产总值和全社会固定资产投资额数据的中位数离下四分位数比离上四分位数近得多，数据均呈现出左偏分布，并且地区生产总值有三个明显的离群值。三个离群值分别为广东省，江苏省和山东省的地区生产总值，笔者认为，是由于上述三省为沿海省份，经济更为发达而导致的。

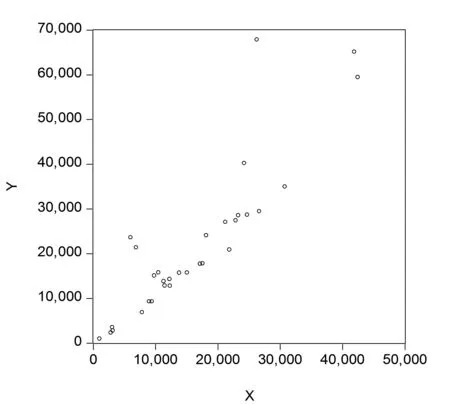
图1 各地区生产总值与全社会固定资产投资额的散点图

图2 各地区生产总值与全社会固定资产投资额的箱线图

通过对各地区生产总值和全社会固定资产投资额茎叶图的绘制，如图3、图4所示，可以直观地看出，这两个批的分布均是偏斜的，且各地生产总值还有三个边远数据点。与从箱线图中得出的结论一致。

图3 地区生产总值茎叶图

图4 全社会固定资产投资茎叶图

3.2 线性分析——最小二乘法

通过对地区生产总值与全社会固定资产投资额的简单线性分析可知，地区生产总值与全社会固定资产投资额之间的相关系数为0.777 854，调整后的相关系数为0.770 194，且通过了t检验和F检验，符合假设检验的条件。但由于调整后的相关系数只有0.770 194，故拟合效果不是很理想。

表2 最小二乘法回归结果

根据相关数据进行最小二乘回归分析，可以得到的最小二乘法模型为：

(1)

(2726.172) (0.141 014)

t=(-0.406 127) (10.076 95)

R2=0.777 854F=101.545 0n=31

图5 最小二乘法下拟合直线

由于原始数据具有一定的非对称性，并且在地区生产总值数据右侧的尾部有离群值存在，无法正确判断两者的数据分布情况，考虑到严谨性，我们尝试进行数据变换。

4 数据变换

霍格林指出：数据变换可以保持批中数据的次序；可以保持一个批的字母值，不计由于数据点之间作内插造成的小差异；保证了原始批中非常靠近的点，在重新表达后批中也非常靠近，至少相对于新尺度很靠近；保证函数没有尖锐的拐角；并且由初等函数来规定，以便差不多用最简单的手持计算器就可以快而方便地做重新表达。因此数据变换可以达到令人满意的效果，下面进行一系列的数据变换，以期将不对称的数据变为对称的数据，并且消除异常值。

4.1 以10为底的对数尺度数据变换

将地区生产总值和全社会固定资产投资额进行对数变换后，分别对数据做出箱线图,如图6所示。

图6 分别对地区生产总值和全社会固定资产投资额进行对数变换后的箱线图

通过箱线图可以看出，经过对数变换后，这两个批的数据与变换前相比较为对称，但是离群值变多。由于最小二乘回归线不提供耐抗性，一个野的数据点就可以支配控制拟合线，若用这两个新的数据批，估计出的参数就不稳定，显然，对数变换的效果不理想。

4.2 平方根变换

为方便表示，记A=Y^1/2，B=X^1/2,做出箱线图,如图7所示。

图7 分别对地区生产总值和全社会固定资产投资额开平方根后的箱线图

通过箱线图可以看出，经过平方根变换后，这两个批的数据均比较对称，且对全社会固定资产投资额进行平方根变换后，没有离群值的存在，但地区生产总值经平方根变换后存在三个异常值。因此，平方根变换的效果不够理想。

4.3 四次方根变换

为方便表示，记M=Y^1/4，N=X^1/4。对数据做出箱线图，如图8所示。

图8 分别对地区生产总值和全社会固定资产投资额开四次方根后的箱线图

观察箱线图，可以发现经过四次方根变换后，这两个批的数据均比较对称，但地区生产总值经四次方根变换后存在两个异常值，全社会固定资产投资额经四次方根变换后存在一个离群值。因此，经过四次方根变换后，这两个批的异常值并不能消失，由于野值使OLS法估计出的参数不稳定，因此，四次方根变换同样不能达到理想的效果。

5 三组耐抗线分析

经过上述数据变换，这两个批中的异常值并不能被消除，考虑到对经济意义的解释，我们不再继续进行数据变换。由于最小二乘回归线不提供耐抗性，一个野的数据点就可以支配控制拟合线，使它给出一个完全引入歧途的Y和X之间关系的概括公式，而三组耐抗线则避免了这个困难，因此我们采用三组耐抗线的方法对各地区生产总值(Y)和全社会固定资产投资额(X)的关系进行探索。

对于数据(x,y)，首先把x的值按升序排序使得x1≤x2≤…≤xn，然后在这些排过序的值的基础上，将(xi,yi)分割成三个组(左组，中组，右组)，使组的大小尽可能的相等,见表3。

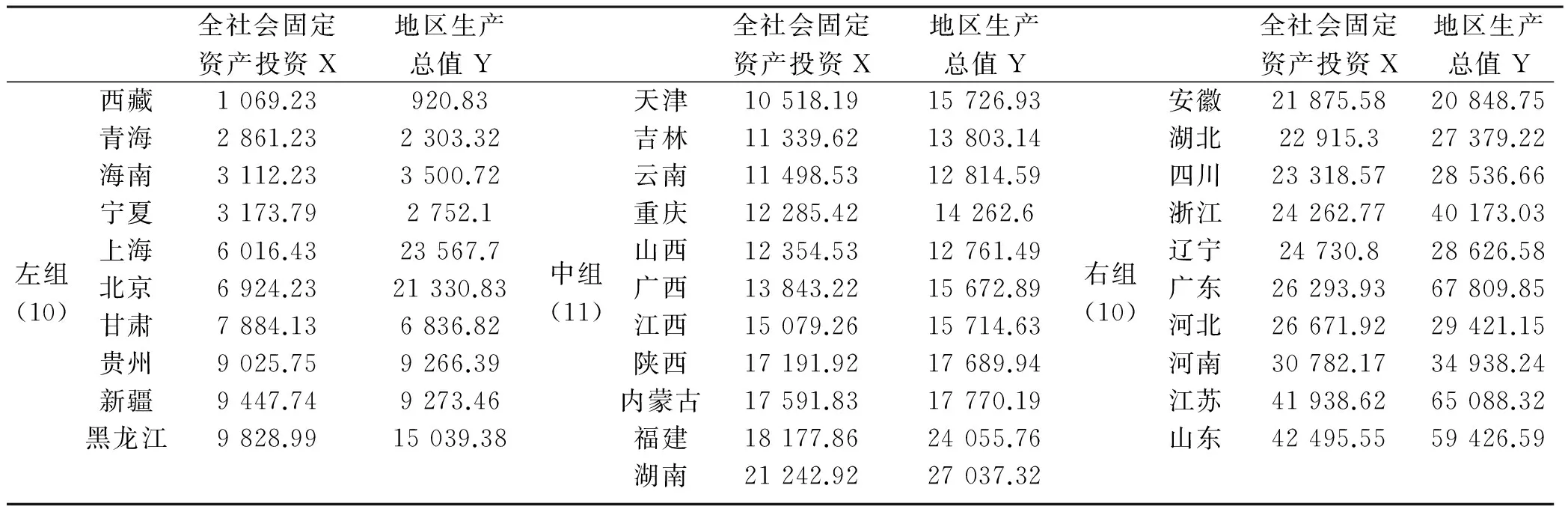
表3 分组后数据

在三个组中，我们分别求出x和y的中位数，得到三个组的总括点(XL,XL),(XM,XM)，以及(XR,YR)。组内总括点使得拟合线具有耐抗性，为了更好地拟合数据，我们以斜率b0和中心值XM来进行拟合。求得的(XL,YL),(XM,YM),(XR,YR)，分别为(6 470.33，8 051.605)，(13 843.22，15 714.63)，(25 512.365，32 179.695)。因此初始斜率为：

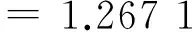
(2)

(3)

数据点分成的三个组以及初始线的残差，见表4。

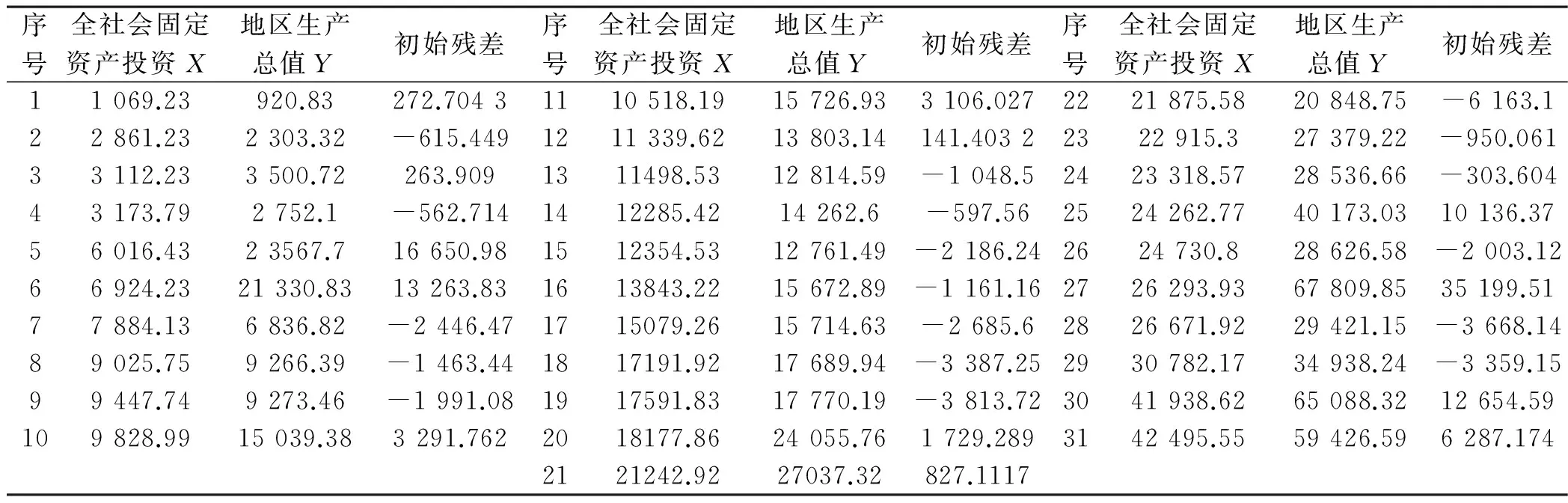
表4 地区生产总值和全社会固定资产投资额——三个组和初始残差

(4)

(5)

因此，一次调整后的斜率为:

(6)

(7)

可以看到，δ1按绝对值大小比b0小得多，但超过了b0绝对值的1 %，还不是可以忽略不计的。于是，做第二步迭代。分别求出X和R(1)的中位数，得到三个组的总括点：(6 470.33，133.475 271 3)，(13 843.22，-534.939 879 3)，(25 512.365，178.002 558 6)，通过计算可以得出：

(8)

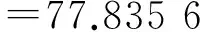
(9)

因此，二次迭代后斜率为:

(10)

(11)

可以看到，δ2的绝对值比b0的绝对值小得多，且小于b0绝对值的1 %(0.012 671)，于是停止迭代。因此，结果的拟合线为：

(12)

图9 三组耐抗线下拟合直线

离这条线的残差对全社会固定资产投资额(X)的散点图如图10所示。

图10 拟合耐抗线后地区生产总值残差对全社会固定资产投资额散点图

总体来看，除去在外值之后，散点图较为平坦。可以看出，稍微异常的数据点几乎对于概括了数据主体部分的直线没有影响。

图11 最小二乘回归残差对全社会固定资产投资额散点图

上图为最小二乘残差对全社会固定资产总额的散点图，可以看出它与图10很相似，但是这个图提示一个略微向下的趋势。这就是说，如果去掉一个稍微负斜率的直线后，最小二乘残差看起来会更水平一些。

6 最小二乘分析模型优化

6.1 异常点分析

6.1.1 残差图

(13)

将各省的全社会固定资产投资(X)与其残差(ri)画图分析，见图12。

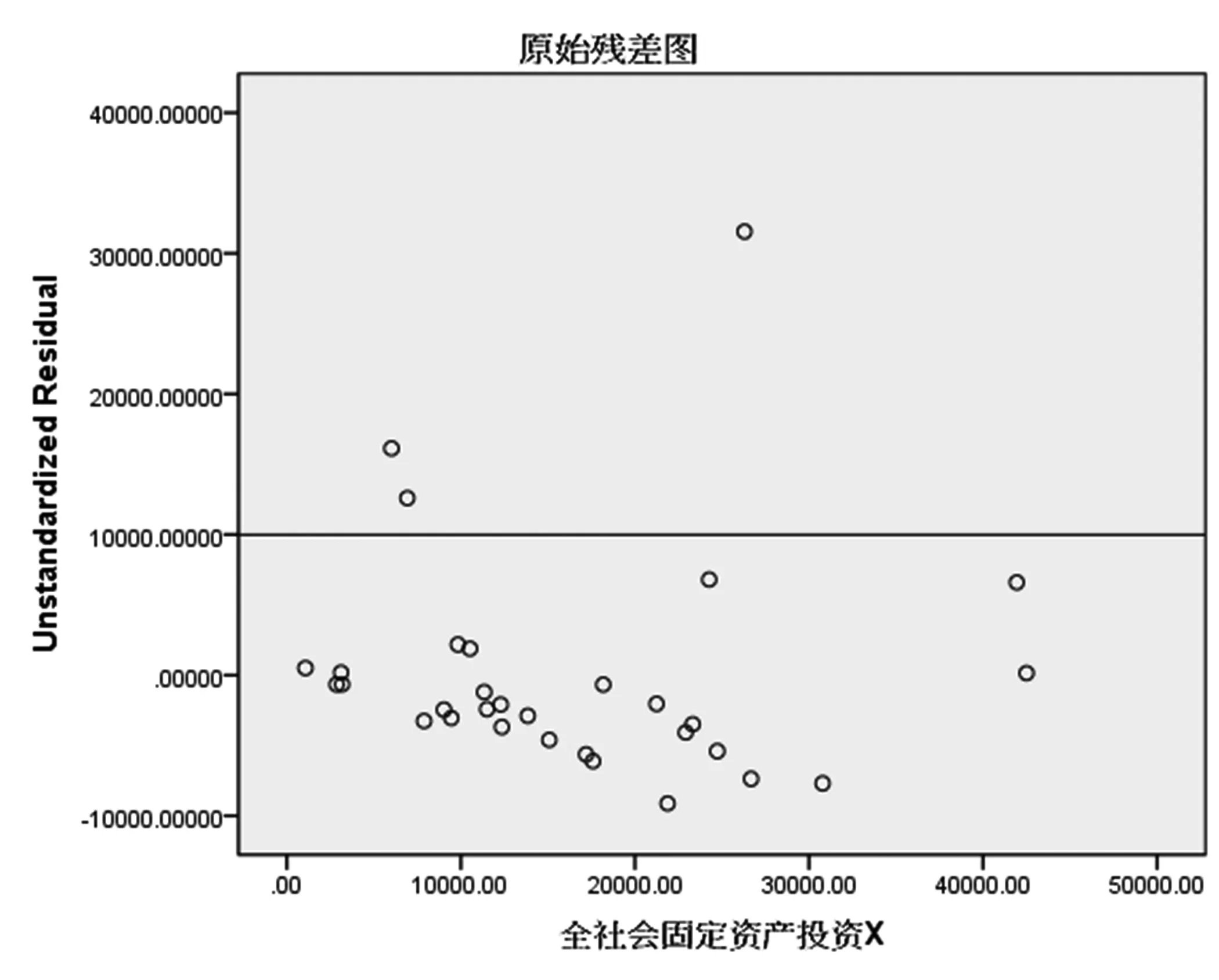
图12 最小二乘回归原始残差图

由图12可看到有一个点明显超出10 000的范围，而另两个点也略超出10 000，则可判定有异常值的存在。严重超出1 000的样本为广东，略超出10 000的有上海、北京。

6.1.2 杠杆率图

(14)

图13 杠杆率图

在本实例中，由于此模型为一元线性回归模型，只有截距与斜率两个参数，又因为一共有31个样本数据，因此这31个残差的平均杠杆率为2 /31，即0. 064 5。而从图中可以看出有两个残差的杠杆率远远大于其平均杠杆率，即山东和江苏，有一个残差的杠杆率略微大于其平均杠杆率，为西藏。

6.1.3 标准化残差图

(15)

(16)

(17)

(18)

从图14可以看出，由于标准化后的残差消除了异方差，且服从正态分布，则其标准化残差的绝对值超过Za/2(1.96)的概率为0.05，而由图看出有一个值明显超出了1.96，还有一个值略微超过1.96，可找到超过1.96的异常值分别为广东、上海。

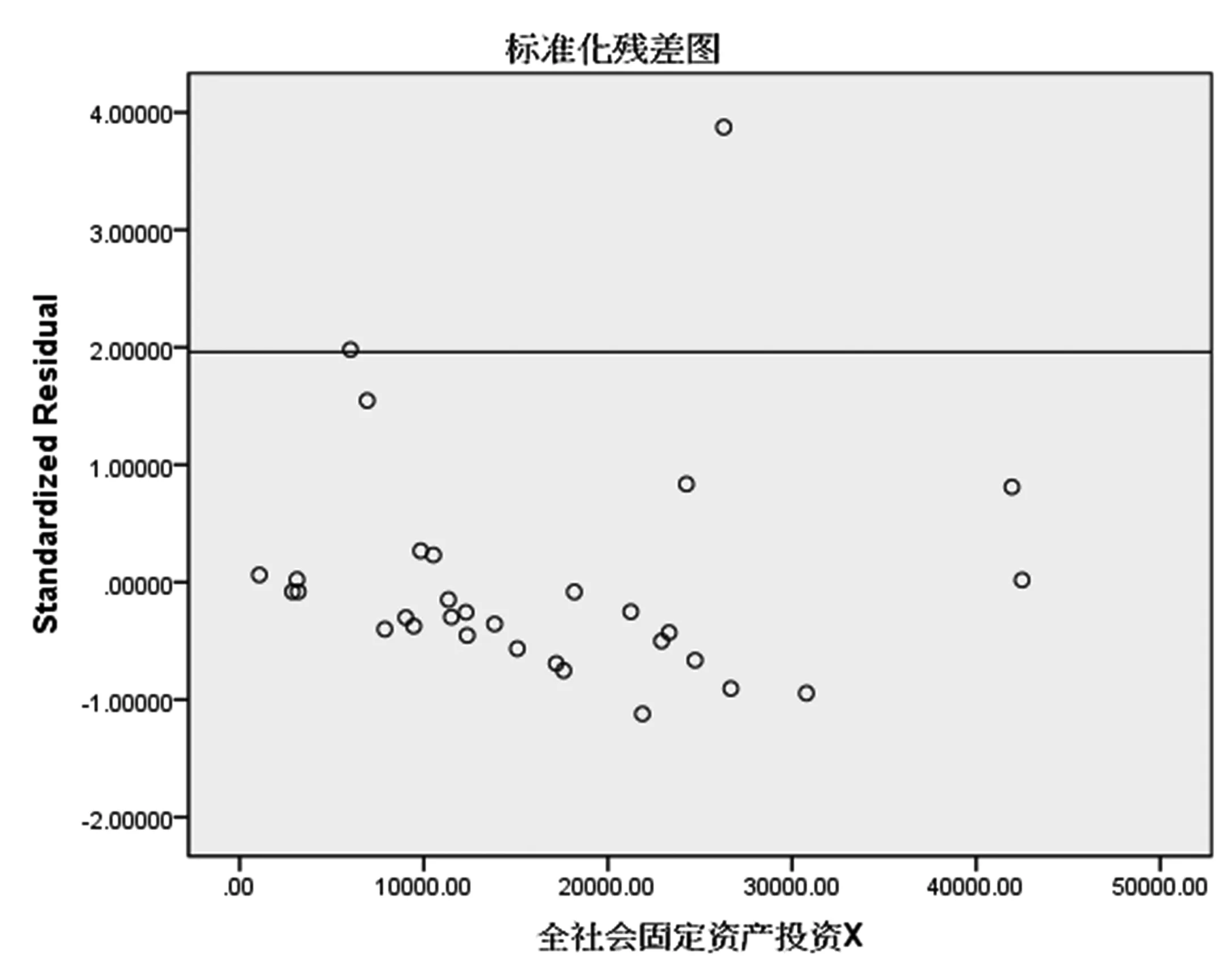
图14 标准化残差图

6.1.4.残差箱线图

从上四分数Fu向上跨出dF的3/2倍，从下四分数向下跨出dF的3/2倍，得到两个截断点，把这两个截断点之外的观测值当作离群值。根据这一定义，直接画出残差的箱线图即可一目了然地发现离群值，即广东、上海、北京、浙江四地,如图15所示。

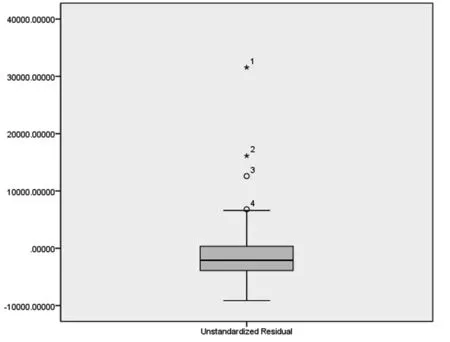
图15 残差箱线图

通过以上对于异常点的不同分析，可看出广东、上海在4种方式的异常点判断中均出现了三次，但广东每次都是远远超出标准，而上海有两次都是超出标准不多；北京出现了两次，且每次都是稍微超出标准而被选为异常点；山东、江苏、浙江、西藏仅仅出现了一次。综合以上分析，笔者认为应将广东省剔除，以避免异常值对于回归拟合的影响。

6.2 模型优化

将广东省对应的数据剔除之后，再次进行最小二乘回归，回归结果如下：

表5 改进后的最小二乘法回归结果

(19)

(185 9.479) (0.097 576)

t=(-0.295 814) (13.531 30)

R2=0.867 359 F=183.096 1 n=30

图16 改进后的散点图和拟合直线

6.3 模型优化效果评价

用均方误差来比较直接用最小二乘法拟合的直线与剔除异常点后用最小二乘法拟合的直线效果的优劣。

通过计算得出最初的最小二乘回归的均方误差为6.193 5×107，优化后的均方误差为2.873 3×107，由此明显看出去掉一个离群点后的拟合偏误要小得多，模型的优化是有效的。

7 三组耐抗线与最小二乘法的比较

由三组耐抗线算得的均方误差为7.332 9×107，大于用最初的最小二乘法算出的均方误差6.193 5×107。

图17 原始数据下三组耐抗线与最小二乘法残差的比较

将原始样本数据的最小二乘法计算于三组耐抗线计算所得到的残差画在一张图中，得到图17。其中蓝色的圈代表运用最小二乘法拟合得到的残差，绿色的圈表示运用三组耐抗线进行拟合后得到的残差。

通过观察残差对X(全社会固定资产投资额)的散点图可以发现，运用三组耐抗线方法得到的残差中有距离均值非常远的点，而最小二乘法得到的残差到中心的距离则没有三组耐抗线的残差距中心远。由此可以看出，三组耐抗线本身具有耐抗性，它不因个别偏离较大的点而剧烈影响所拟合的参数值。因此即便有差异很大的点，它也会将离群点对拟合参数的影响降到很小，因此在残差图上就可能出现某些离群点距离拟合直线上对应点的距离很大的情况。而最小二乘法则不然，因为它要使得残差平方和最小，因而考虑到了包括异常值在内的所有的数。对于越偏远的点，最小二乘法的拟合效果越差，因为它为了使残差的平方和最小，可能会舍去其他拟合效果较好的模型。因此对于异常值较多或者偏离较远的情况下，三组耐抗线的方法相对于最小二乘法更加可靠。但在上述数据中，由于仅有一个野值，并且其离群的程度不是很大，因此由三组耐抗线算得的均方误差要大于最小二乘法算出的均方误差。