具有预解算子的随机脉冲积分微分包含∗

李文胜

具有预解算子的随机脉冲积分微分包含∗

李文胜

（西安航空学院理学院西安710077）

利用Krasnoselskii-Scheafer型集值映射不动点定理结合预解算子理论，在公理化定义的相空间上，研究了一类随机脉冲中立型积分微分包含温和解的存在性，并建立了此类问题温和解的存在性。

预解算子；随机脉冲；积分微分包含

Class NumberO175.22

1引言

近年来，微分包含温和解的存在性得到了广泛关注［1～5］，有关随机脉冲微分方程的内容可参见文献［6～9］。

本文主要考虑一类具有时滞的随机脉冲集值泛函微分方程：

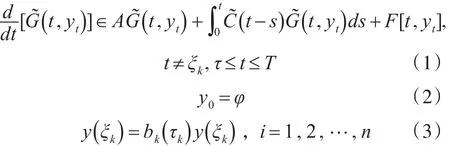
2预备知识

C(Rτ，X)是由从Rτ到X的所有连续泛函组成的Βanach空间，赋予范数‖x‖∞=sup{‖x(t):t∈Rτ‖}。可测泛函x:Rτ→X是Βochner可积当且仅当‖x‖为Lebesgue可积，有关Βochner积分及其性质参见Yosida［10］。L1() Rτ，X是由Βochner可积的连续泛函x:Rτ→X组成的Βanach空间，赋予范数

考虑下面系统：

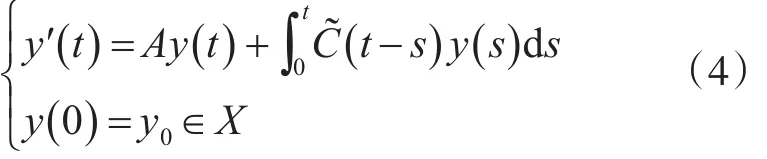
定义1［11］方程（4）的预解算子是一个有界算子泛函R(t)∈L(X)，并且具有如下性质：

1）R(0)=I，I为X上的恒等算子。

2）对每个y∈X，t→R(t) y是强连续的。

3）R(t)∈L(Y~)，t∈Rτ，其中Y~为赋予图像范数的Banach空间D(A)。若y∈Y~，有

R(·)y=C1(J，X)∩C(J，Y~)且

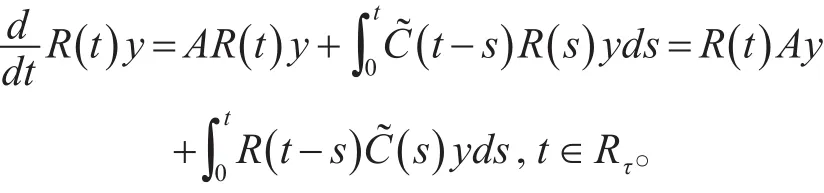
引理1［12］假设以下两个条件成立：

1）A是空间X上的一个稠定的闭线性算子且生成一个强连续半群T() t。

2）{C~(t)，t∈Rτ}是从Y到X的闭线性算子

族，并且，存在可积函数c:Rτ→R+。使得对每个

c(t)|y|，y∈Y，t∈Rτ，则存在一个常数H=H(T)，使得‖R(t+h)-R(h) R(t)‖L(X)≤Hh，0≤h≤t≤T。

引理2［13～15］若多值映射F有非空紧值且全连续，则F是上半连续的当且仅当F有闭图像（即当xn→x*，yn→y*，yn∈F(xn)时，有y*∈F(x*)。

定义2称F:Rτ×B→P(X)为Caratheodory多值映射，如果

1）对每个ψ∈B，t→F(t，ψ)是可测的；

2）对任意的t∈Rτ，ψ→F(t，ψ)为上半连续的。

引理3［13］如果F为Caratheodory多值映射，且对给定的ψ∈B，集合SF，ψ={f∈L1(Rτ，X): f(t)∈F(t，ψ)，t∈Rτ}是非空的，Γ:L1(Rτ，X)→C(Rτ，X)为线性连续映射，则Γ◦SF:C(Rτ，X)→Pcp，cv(C(Rτ，X))，y→(Γ◦SF)(y)=Γ(SF，y)是 C(Rτ，X)×C(Rτ，X)上的闭图算子。

有关公理化定义的相空间B，可参见文献［5，14］

定义3泛函{y(t):t0-r≤t≤T}称为系统（1）-（3）的温和解，当且仅当

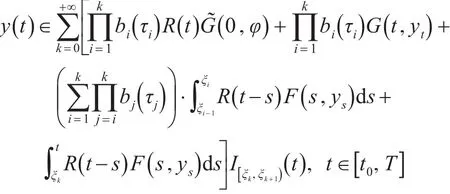
引理4［12］若多值映射Γ1:X→Pbd，cl，cv() X和Γ2:X→Pcp，cv() X满足：

1）Γ1是压缩算子；2）Γ2是全连续的；那么

（1）当λ=1时，算子包含λx∈Α1x+Α2x有一个解，或者；

（2）集合{}

u∈λΑ1u+λΑ1u，0＜λ＜1是无界的。

3主要结果

为了证明系统（1）～（3）温和解的存在性，假设下面条件成立：

H1.R(t)是紧算子，且存在一个常数M＞0，使得当t∈Rτ时，‖R(t)‖≤M。

H2.G:Rτ×B→D是连续函数，且对任意的(t，ψi)∈Rτ×B，存在L＞0，使得

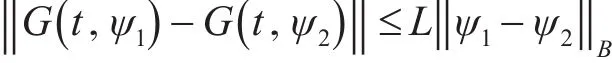
并且，对于t∈Rτ，ψ∈B，存在一个常数L0＞0，使得

H3.（1）F:Rτ×B→Pbd，cv，cp(X)；且对每个ψ∈B，t→F(t，ψ)是可测的；对任意的t∈Rτ，ψ→F(t，ψ)是上半连续的；对给定的ψ∈B，集合SF，ψ={f∈L1(Rτ，X):f(t)∈F(t，ψ)a.e.t∈Rτ}是非空的。

（2）对每个正常数rˉ，存在正函数Θrˉ∈L1()

Rτ，R+，使得

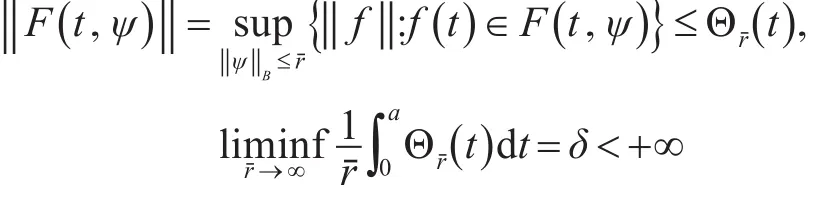
H4.存在常数Q＞0，使得

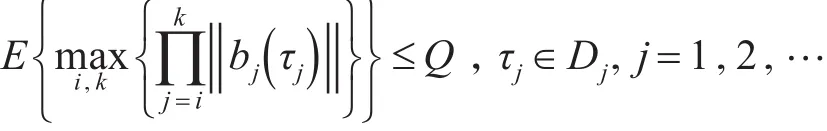
备注1［9］假设φ∈B且t≤0。φt为定义成φt(θ)=φ(t+θ)形式的泛函。所以，如果公理（a）中的泛函x(·)使得x0=φ，则xt=φt。

备注2［16～17］令Ma=supt∈RτM(t)，Ka=maxt∈RτK(t)，并且M*=M max{eωa，1}。

定理1假设φ∈B且条件H1-H4成立。如果

则系统（1）-（3）的温和解是存在的。

证明令BˉT={y:(-∞，T]→X;y0∈B，y|R∈

τC(Rτ，X)}，对每个y∈BˉT记‖·‖a是BˉT的半范数并定义为

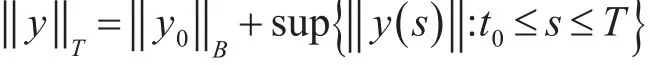
定义多值映射N:BˉT→P(BˉT)，对任意的y∈BˉT，Ny是所有的ℜˉ∈BˉT组成的集合，使得

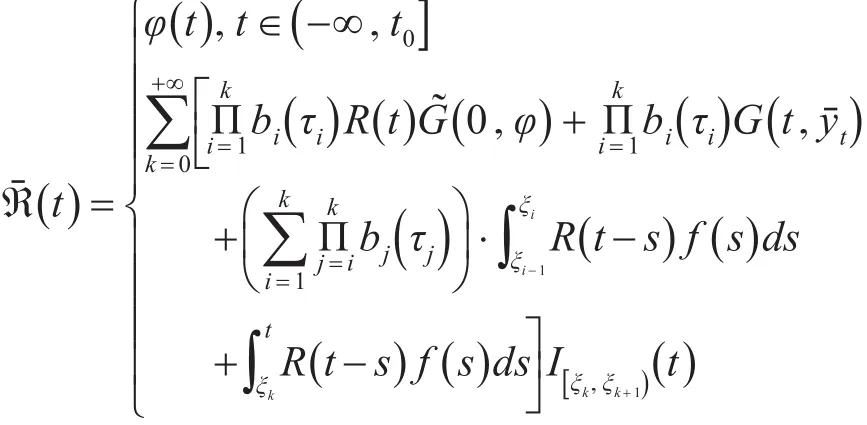
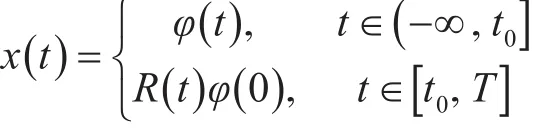
令y(t)=z(t)+x(t)，t∈(-∞，T]，要使y满足定义3中的随机脉冲积分包含当且仅当z满足z0=0且

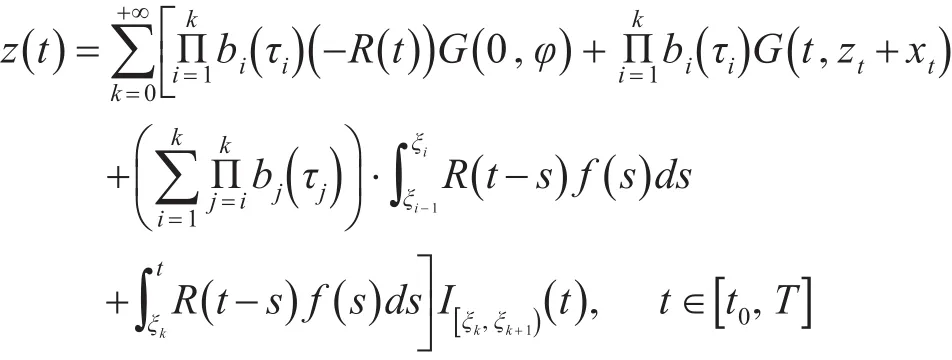
其中SF，z={f∈L1([t0，T]，X):f(t)∈F(t，zs+xs)，a.e.t∈[t0，T]}。

考虑空间BˉT0={z∈BˉT:z0=0}。记‖·‖T是BˉT0的半范数且定义为

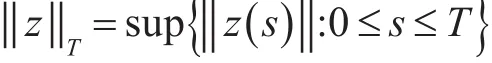
显然(BˉT0，‖·‖T)是一个Banach空间。

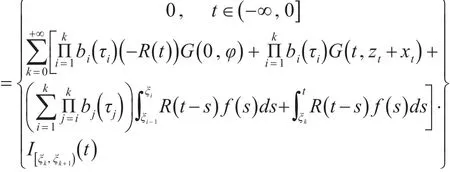
为了应用引理4，将证明分为下面几步：

第一步，集合{u∈Bˉ0T:u∈λN^u，0＜λ＜1}是有界的。

令z∈{u∈BˉT0:u∈λN^u，0＜λ＜1}，则存在g∈SF，z，使得

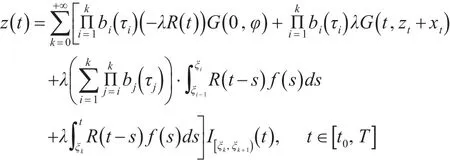
同样建立一个积分包含z∈λN^z，λ∈(0，1)的解的先验估计。设zλ是z∈λN^z，λ∈(0，1)的一个解。由μλ(s)=supθ∈[0，s]‖zλ(θ)‖可知，对任意的s∈[t0，T]，有

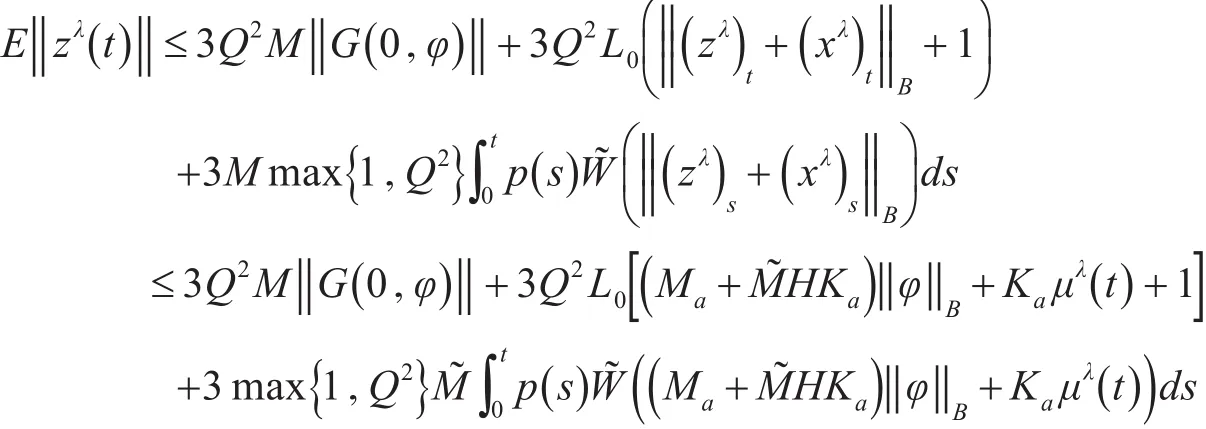
因此

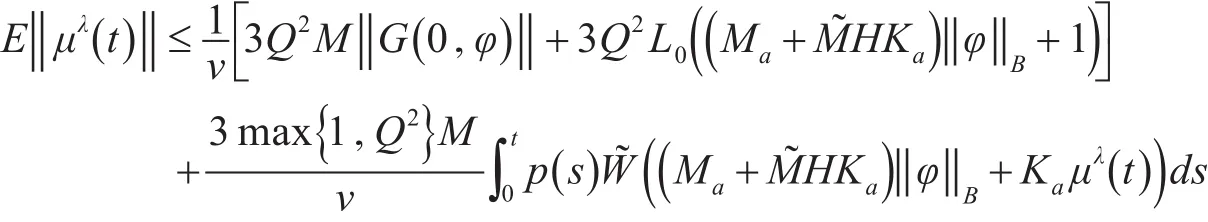
定义χλ(t)=(Ma+J~+M H Ka)‖φ‖B+Kaμλ(t)，可得

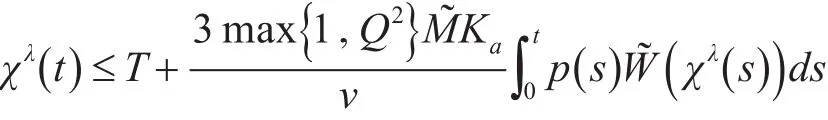
记上述不等式的右端为ζλ() t，从而

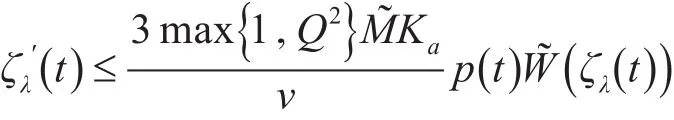
因而

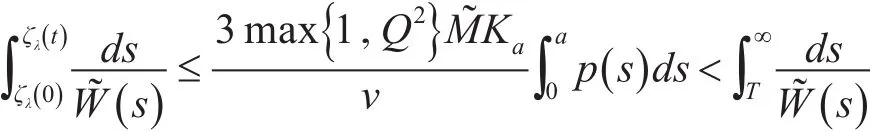
由此可知集合{u∈Bˉ0a:u∈λN~u，0＜λ＜1}是有界的。

第二步，N^有闭图。

令zn→z*，ℜˉn0∈N^(zn)，及ℜˉ0n→ℜˉ*0，下面证明事实上，如果ℜˉn0∈N^(zn)，那么存在，使得对任意的t∈J，都有

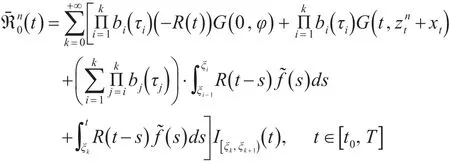
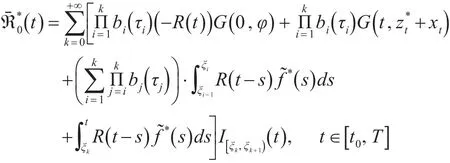
易知当n→∞时

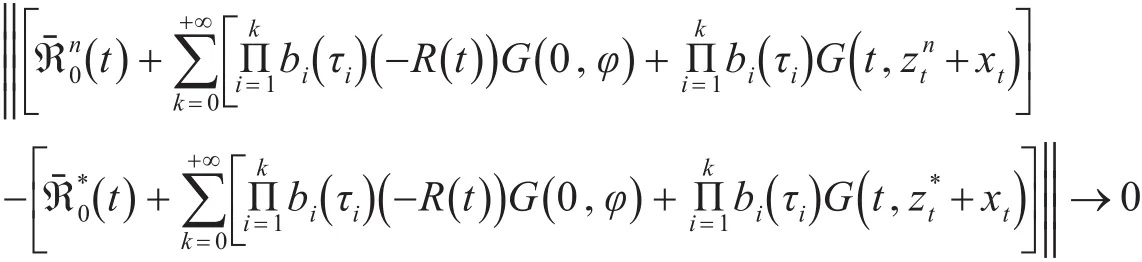
考虑如下线性连续算子

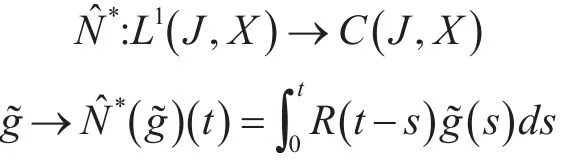
由引理3可得，N^*◦SF是闭图算子，此外

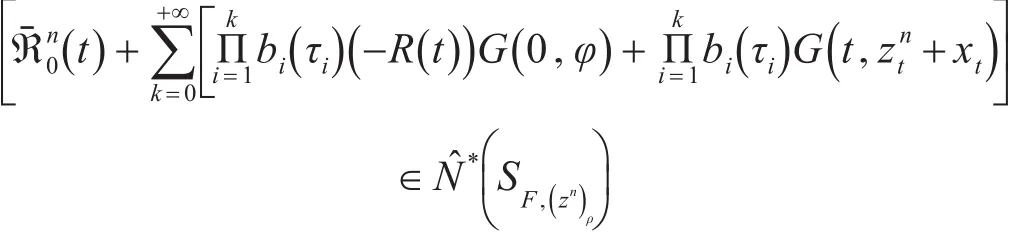
因为zn→z*，从引理3可得

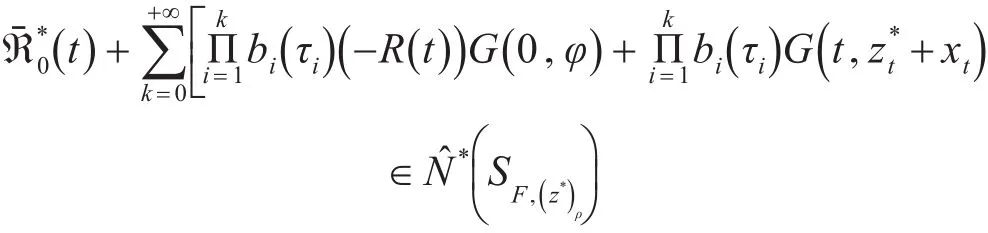
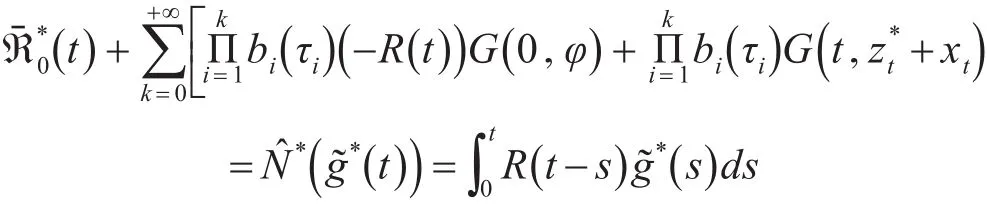
由此可得，N^有闭图。

我们将N~分解为N^=N^1+N^2，其中

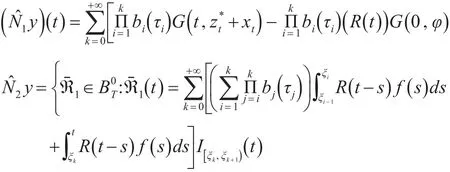
第三步，N^1是压缩算子。

对任意的z*，z**∈Br，可得

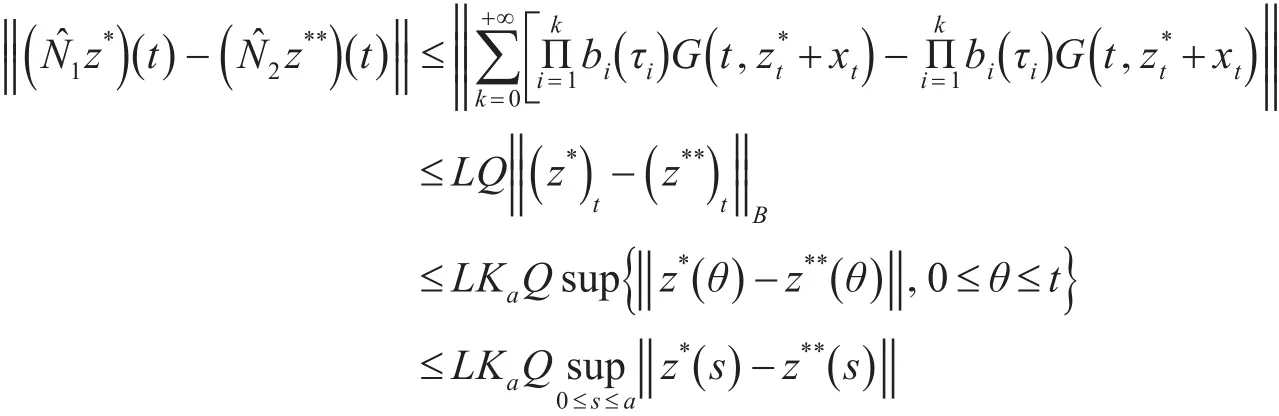
故

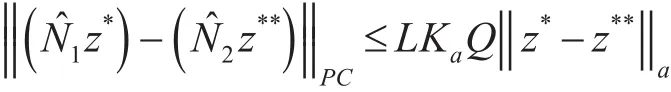
因为LKaQ＜1，所以N^1是压缩算子。类似于文献［8］，N^2是全连续多值映射。由引理4知，具有预解算子的随机脉冲积分微分包含问题（1）～（3）至少有一个温和解。

4结语

利用预解算子理论结合相应的集值映射不动点定理，先将模型转化成积分方程，在给定条件及多值映射有关理论的基础上，按照不动点定理，逐步证明了随机脉冲中立型积分微分包含温和解的存在性。该方法对同类复杂模型的研究具有促进意义。

［1］Lin A，Hu L.Existence results for impulsive neutral sto⁃chastic functional integro-differential inclusions with nonlocal initial［J］.Conditions.Comput.Math.Appl，2010，59（1）：64-73.

［2］Balasubramaniam P，Ntouyas S K.Controllability for neu⁃tral stochastic functional differential inclusions with infi⁃nite delay in abstract space［J］.J.Math.Anal.Appl，2006，324（1）：161-176.

［3］Li W-S，Chang Y-K，Nieto J.J.Solvability of impulsive neutral evolution differential inclusions with state-depen⁃dent delay，Math Comput.Modelling［J］.2009，49（9-10）：1920-1927.

［4］Chang Y-K，Anguraj A，Mallika Arjunan M.Existence re⁃sults for non-densely defined neutral impulsive differen⁃tial inclusions with nonlocal conditions［J］.Journal of Ap⁃plied Mathematics and Computing，2008，28（1-2）：79-91.

［5］李文胜.时滞依赖状态的非自治多值偏积分微分方程［J］.数学物理学报，2014，34（1）：139-149.

LI Wensheng.On non-autonomous multivalued partial in⁃tegro-differential equations with state-dependent delay［J］.Acta Mathematica scientia，2014，34（1）：139-149.

［6］Wu S J，Duan Y R.Oscillation，stability and bounded⁃ness ofsecond-order differential systems with random im⁃pulses［J］.Comput.Math.Appl，2005，49（9-10）：1375-1386.

［7］Anguraj A，Wu S J.Vinodkumar A.The existence and ex⁃ponential stability of semi-linear functional differential equations with random impulses under non-uniqueness［J］.Nonlinear Anal.TMA，2011，74（2）：331-342.

［8］李文胜，周千，韩慧蓉.随机脉冲随机偏发展微分包含解的存在性［J］.应用数学学报，2015，38（6）：1059-1073.

LI Wensheng，ZHOU Qian，HAN Huirong.Existence re⁃sults for a stochastic partial evolution differential inclu⁃sions with random impulses［J］.Acta Mathematicae Appli⁃catae Sinica，2015，38（6）：1059-1073.

［9］Zhao Zhi-Han，Chang Yong-Kui，Li Wen-Sheng.Asymp⁃totically almost periodic，almost periodic and pseudo-al⁃most periodic mild solutions for neutral differential equa⁃tions［J］.Nonlinear Analysis：Real World Applications，2010，11（4）：3037-3044.

［10］K.Yosida，Functional Analysis［M］.6th ed.，Spring⁃er-Verlag，Berlin，1980.

［11］Lasota A，Opial Z.An application of the Kakutani-Ky Fan theorem in the theory of ordinary differential equa⁃tions.Bulletin de I'Academie Polonaise des Sciences，Se⁃rie des Sciences［J］.Mathematiques，Astronomiques et Physiques，1965，13：781-786.

［12］Hernández E.Existence results for partialneutralintegro⁃differential equations with unbounded delay［J］.J Math AnalAppl，2004，292：194-210.

［13］Lasota A，Opial Z.An application of the Kakutani-Ky Fan theorem in the theory of ordinary differential equa⁃tions.Bulletin de I'Academie Polonaise des Sciences，Se⁃rie des Sciences［J］.Mathematiques，Astronomiques et Physiques，1965，13：781-786.

［14］Pazy A.Semigroups of Linear Operators and Applications to Partial Differential Equations［M］.in：Applied Mathe⁃matical Sciences，vol.44，New York：Springer-Verlag，1983.

［15］Fitzgibbon W E.Semilinear functional differential equa⁃tions in Banach spaces［J］.Journal of Differential Equa⁃tions，1978，29（1）：1-14.

［16］Grimmer R.Resolvent operators for integral equations in a Banach space［J］.Transactions of the American Mathe⁃matical Society，1982，273（1）：333-349.

［17］Liang J，Liu J H，Xiao T-J.Nonlocal impulsive problems for integrodifferential equations.The sixth International Conference on Differential Equations and Dynamical Sys⁃tems［M］.Baltimore，Maryland，USA，2008：22-26.

Existence Results of Mild Solution for Random Impulsive Integro-differentialInclusions with Resolvent Operator

LI Wensheng
（Faculty of Science，Xi'an Aeronautical University，Xi'an 710077）

This paper is concerned with existence of mild solution for a random impulsive integro-differential inclusions with resolvent operator.Using Krasnoselskii-Scheafer type fixed point theorems and the theory of Resolvent operator，the existence of mild solutions is obtained in the axiomatic definition ofthe phase space.

resolventoperator，random impulsive，integro-differentialinclusions

O175.22

10.3969/j.issn.1672-9722.2017.08.006

2017年3月2日，

2017年4月10日

陕西省教育厅科研项目（编号：15JK1379）；西安航空学院科研基金（编号：2014KY1210）资助。

李文胜，男，硕士，研究方向：算子理论与微分方程。