基于讨论机制的混合蛙跳算法∗
2017-09-12王俊徐建中徐雷
王俊徐建中徐雷
基于讨论机制的混合蛙跳算法∗
王俊徐建中徐雷
(南京理工大学南京210094)
针对混合蛙跳算法易陷入局部最优的情况,提出一种基于讨论机制的混合蛙跳算法。改进算法在原混合蛙跳算法基础上加入了讨论机制,并根据迭代次数动态调整讨论次数,增加算法后期变异性,避免陷入局部最优。论文选择了3个常用的测试函数进行测试,与基本蛙跳算法比较,在计算精度和求解成功率上均有很大的提高。
混合蛙跳算法;讨论机制;动态调整;计算精度;成功率
Class NumberTP301.6
1引言
混合蛙跳算法(Shuffled Frog Leaping Algo⁃rithm)是一种高效的智能算法,由于算法的简单、易实现等特点而被广泛使用。为了提高算法的性能,国外[1~11]和国内学者[12~18]做了很多研究。Hu等[10]在基础的混合蛙跳算法中加入了记忆因子,通过因子的自适应变化,提高了算法的成功率。Wang等[11]在基础混合蛙跳算法中,加入了一种自适应模糊变异策略,有效地提高了算法的精度。张等[12]将模拟退火和免疫接种思想引入到混合蛙跳算法中,有效地克服了局部极值,提高了算法的收敛速度和准确度。刘等[13]引入共享因子的思想,将其分为全局共享因子和局部共享因子,该算法在单峰值和多峰值函数优化问题上具有较高的收敛速度和精度。本文不修改原算法的内部搜索策略,而是增加了一个讨论机制,在内部更新完之后,每隔一定代数就进行一次讨论,并且随着代数增加,逐渐增加讨论频率。仿真结果表明,本文算法在求解精度和正确率方面都取得较好效果,有效地提升了算法的性能。
2混合蛙跳算法
混合蛙跳算法是受自然界中青蛙觅食启发而产生的进化算法。其思想是:一组青蛙分组去寻找食物,每组都有自己的文化,每个青蛙都往离食物近的青蛙移动,并且互相交流,按照这个思想每组执行局部搜索,当执行一段时间局部搜索后各组会进行交流,持续这个过程直到条件满足为止,混合蛙跳算法主要包括三个过程:子群划分,内部搜索和全局交换。
1)子群划分
设种群内有N个个体,将其分成k组,每组的个体数为N/k,用Xi=(xi1,xi2,…,xiD)表示第i个个体,D表示个体的维数。对于初始种群S=(X1,X2,…,XN),按适应度升序排列后,将第一个个体放入第一个子群,第二个个体放入第二个子群,…,第k个放入k组,第k+1,k+2,等依次放入第一组,第二组。依次重复直到所有个体都被分入组中。
2)子群内部搜索
设Xb为每组中适应度最好的个体,Xw为每组中适应度最差的个体,Xg为所有个体中适应度最好的个体。对每组进行内部搜索,即更新最差个体,更新公式如式(1)所示
其中,Xw′为产生的新的个体,r是随机数,取值为0~1,如果新产生的个体比原来的Xw好,就替代原来的个体。如果适应度上没有改进则采用式(2)进行更新。
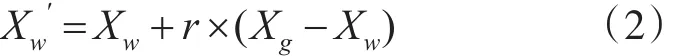
如果新个体适应度上还是没有改进就随机产生一个个体替换Xw。
3)全局信息交换
当所有子群更新完成之后,重新进行子群划分。并进行内部搜索,反复执行此过程直到满足终止条件或者达到进化代数为止。
3算法改进
3.1讨论机制
混合蛙跳算法由于后期变异性差,因此很容易陷入局部最优情况。本文在每进化m代后,在原有的组内搜索结束后进行讨论。
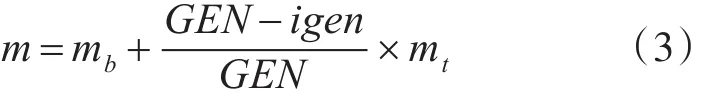
其中,G EN为总进化代数,igen为当前进化代数,mb和mt是两个常量,实验中取值为1和7,可以看出,随着进化代数的增加m逐渐减小,以此来增加算法后期的变异性,避免陷入局部最优,具体为
1)随机选择一个组,并将组中最优个体加上一个随机变化生成新个体:
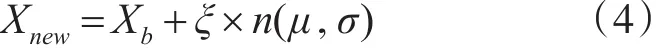
2)随机选择一个组,并随机选择一个个体加上随机变化生成新个体:
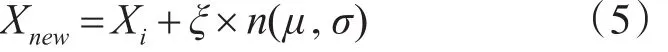
3)随机选择一个组,并随机选择两个个体融合产生新个体。
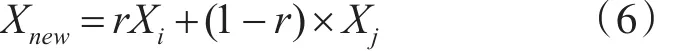
其中n(μ,σ)为高斯函数,μ为均值,σ为方差,实验中取值0和1,ξ为步长,其取值计算公式为
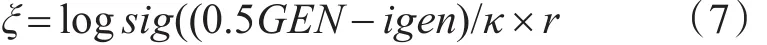
其中,κ控制函数坡度,实验中取值为25,通过p1,p2来确定选择哪种方案,具体为:随机产生一个0~1之间的数τ1,当τ1<p1选择方案1,当τ1>p1再产生一个随机数τ2,当τ2<p2选择方案2,当τ2>p2选择方案3。将新产生的个体与组内最差个体比较,如果优于组内最差个体比较,则替换。
3.2改进后的算法流程
设种群内有N个个体,将其分成k组,每组的最大内部搜索次数为P,最大进化代数为GEN,适应度函数为f(x)。本文提出的基于讨论机制的混合蛙跳算法流程表示为


4仿真实验
4.1实验设计
为了验证算法的性能,将本文算法(Discussion Mechanism Based Shuffled Frog Leaping Algorithm,DMSFLA)与基本的混合蛙跳算法(SFLA),张等改进算法(Improved Shuffled Frog Leaping Algorithm,ISFLA)做对比,选择三个典型的函数进行测试。分别为
1)Sphere函数
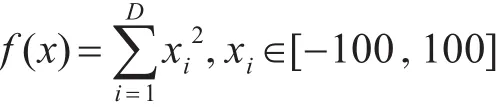
2)Rastrigin函数
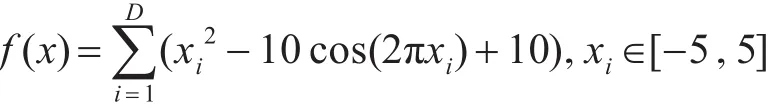
3)Ackley函数
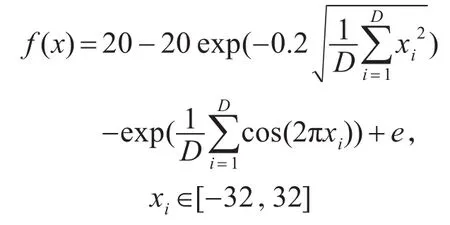
实验参数设置为:GEN=400,种群个数N=100,分组数k=10,子群内部搜索次数P=10。P1=P2= 0.5。实验从算法求解精度和算法求解成功率进行对比。
4.2实验结果及分析
1)算法求解精度对比
针对每一函数独立进行100次实验,表1~3分别给出了实验结果。
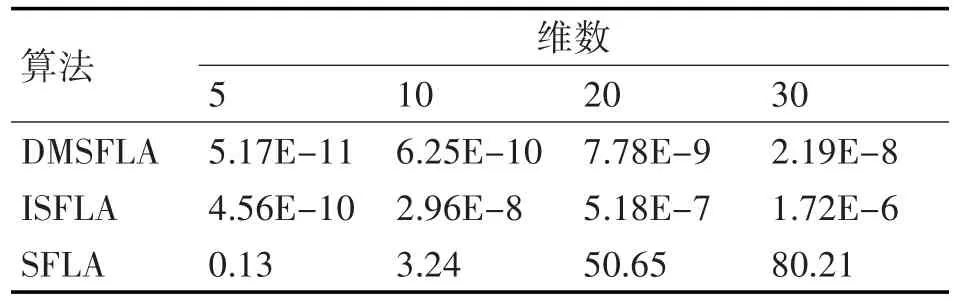
表1 Sphere函数在不同维数下的平均适应度
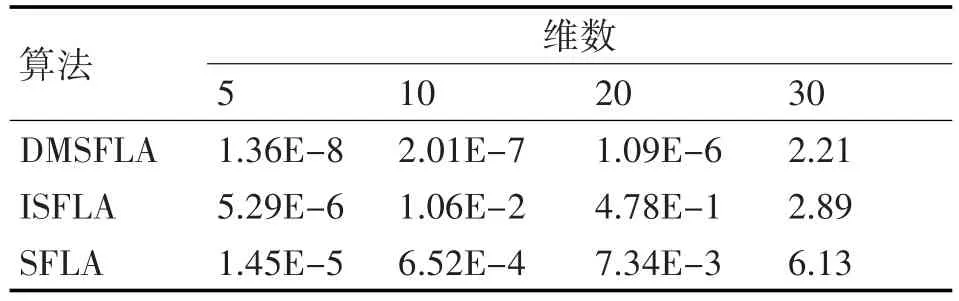
表2 Rastrigin函数在不同维数下的平均适应度
从表1~3可以看出,DMSFLA在Sphere函数中有较好的表现,随着维数的增加,DMSFLA求得平均最优适应度都比另外两种算法小,特别是相对基本SFLA算法有较高的求解精度。在Rastrigin函数的测试中,在维数为5~20之间,有较好的表现。在Ackley函数中在维数为5和10时,相对于SFLA也有明显的提升。
2)算法求解成功率对比
指定各个函数的收敛精度如表4所示,函数的维数取30,每个算法独立100次后结果如表5所示。

表4 函数收敛精度
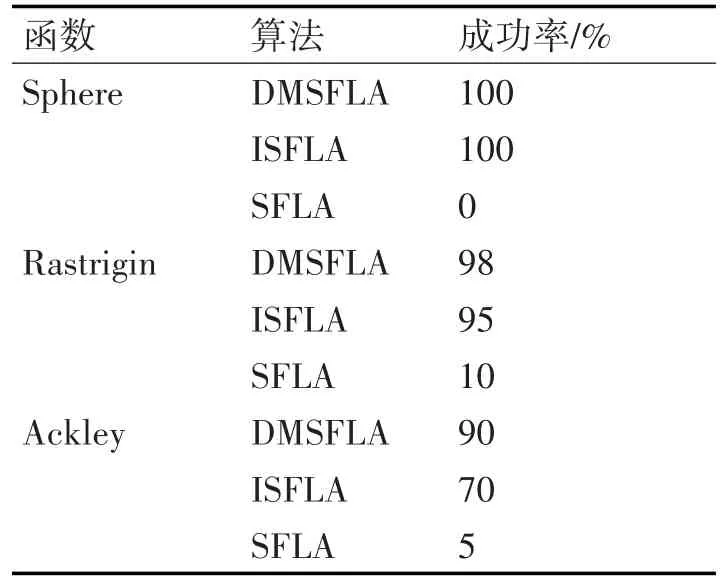
表5 100次实验结果
从表5的结果可以看出,对于3个测试函数,在指定的精度下DMSFLA都能达到较好的成功率。综上分析,本文提出的基于讨论机制的混合蛙跳算法在算法求解精度,成功率方面都有一定的提升,获得了较满意的结果。
5结语
本文对基本的混合蛙跳算法做了一定的改进,通过增加讨论机制,提高了算法后期的搜索能力,避免过早陷入局部最优。实验对3个典型函数进行测试,结果表明,本文提出的改进算法有效提高了算法求解精度和准确率,增强了算法的寻优性能。但是,在Rastrigin函数和Ackley函数的30维数测试中,一定程度上还是会陷入局部最优的情况,没有达到显著的提升,仍有改进的空间。未来,将继续提高算法在高维数的优化能力。
[1]J.Zhou,E.Dutkiewicz,R.P.Liu,X.Huang,G.Fang and Y.Liu.A Modified Shuffled Frog Leaping Algorithm for PAPR Reduction in OFDM Systems[J].in IEEE Transac⁃tions on Broadcasting,2015,61(4):698-709.
[2]A.Asrari,T.Wu,S.Lotfifard.The Impacts of Distributed Energy Sources on Distribution Network Reconfiguration[J].in IEEE Transactions on Energy Conversion,2016,31(2):606-613.
[3]Y.Chen,J.Wen,L.Jiang,S.Cheng.Hybrid algorithm for dynamic economic dispatch with valve-pointeffects[J].in IET Generation,Transmission&Distribution,2013,7(10):1096-1104.
[4]M.A.Bahar,M.Shokooh-Saremi.Design of GMR-based narrow bandpass filters using improved shuffled frog leap⁃ing algorithm[J].in Electronics Letters,2015,51(6):497-499.
[5]H.M.Hasanien.Shuffled frog leaping algorithm-based static synchronous compensator for transient stability im⁃provement of a grid-connected wind farm[J].in IET Re⁃newable Power Generation,2014,8(6):722-730.
[6]W.Ding,J.Wang,Z.Guan,Q.Shi.Enhanced minimum attribute reduction based on quantum-inspired shuffled frog leaping algorithm[J].in Journal of Systems Engineer⁃ing and Electronics,2013,24(3):426-434.
[7]H.Huang,M.Pan,S.Gong.Estimating and calibrating the response of multiple wideband digital radio frequency memories in a hardware-in-the-loop system using shuf⁃fled frog leaping algorithm[J].in IET Radar,Sonar& Navigation,2016,10(5):827-833.
[8]M.Barati,M.M.Farsangi.Solving unitcommitment prob⁃lem by a binary shuffled frog leaping algorithm[J].in IET Generation,Transmission&Distribution,2014,8(6):1050-1060.
[9]H.M.Hasanien.Shuffled Frog Leaping Algorithm for Pho⁃tovoltaic Model Identification[J].in IEEE Transactions on Sustainable Energy,2015,6(2):509-515.
[10]B.Hu,Y.Dai,Y.Su.Feature Selection for Optimized High-dimensional Biomedical Data using the Improved Shuffled Frog Leaping Algorithm[J].in IEEE/ACM Transactions on Computational Biology and Bioinformat⁃ics,2014,3(99):1-1.
[11]F.Wang,C.Geng,L.Su.Parameter identification and prediction of Jiles-Atherton model for DC-biased trans⁃former using improved shuffled frog leaping algorithm and leastsquare supportvector machine[J].in IET Elec⁃tric Power Applications,2015,9(9):660-669.
[12]张潇丹,赵力,邹采荣.一种改进的混合蛙跳算法求解有约束优化问题[J].山东大学学报(工学版),2013,43(1):1-8.
ZHANG Xiaodan,ZHAO Li,ZHOU Cairong.An im⁃proved shuffled frog leaping algorithm for solving con⁃strained optimization problems[J].Journal of Shandong University(Engineering Science),2013,43(1):1-8.
[13]刘立群,王联国,韩俊英.基于全局共享因子的混合蛙跳算法[J].计算机工程,2013(10):162-166.
LIU Liuqun,WANG Lianguo,HAN Junying.Shuffled Frog Leaping Algorithm Based on Global Sharing Factor[J].Computer Engineering,2013(10):162-166.
[14]张沈习,陈楷,龙禹.基于混合蛙跳算法的分布式风电源规划[J].电力系统自动化,2013,37(13):76-82.
ZHANG Shenxi,CHEN Kai,LONG Yu.shuffled frog leaping algorithm based distributed wind power planning[J].Automation of Electric Power Systems,2013,37(13):76-82.
[15]马平莉.混合蛙跳算法研究[D].西安:西安电子科技大学,2013.
MA Pingli.Research on Shuffled Frog Leaping Algorithm[D].Xi'an:Xidian University,2013.
[16]苏仟.混合蛙跳算法研究与改进[D].西安:西安电子科技大学,2014.
SU Qian.Research and Improvement of Shuffled Frog Leaping Algorithm[D].Xi'an:Xidian University,2013.
[17]李建军,郁滨,陈武平.混合蛙跳算法的改进与仿真[J].系统仿真学报,2014,26(4):755-760.
LI Jianjun,YU Bing,CHEN Wuping.Improvement and Simulation for Shuffled Frog Leaping Algorithm[J].Jour⁃nalof System Simulation,2014,26(4):755-760.
[18]施秋红.一种改进的混合蛙跳算法[J].重庆理工大学学报:自然科学版,2013,27(5):78-81.
SHI Qiuhong.An Improved Shuffled Frog Leaping Algo⁃rithm[J].Journal of Chongqing Institute of Technology,2013,27(5):78-81.
Discussion Mechanism Based Shuffled Frog Leaping Algorithm
WANG Jun XU Jianzhong XU Lei
(Nanjing University of Science and Technology,Nanjing 210094)
A discussion mechanism is put forward based shuffled frog leaping algorithm in view of the situation that the shuf⁃fled frog leaping algorithm is easy to fall into local optimal situation.The scheme increases the variability of the algorithm,and avoids falling into local optima by adding a discussion mechanism,and the number of the discussion is adjusted dynamically.The algorithm is tested by three classical test functions,the result shows that compared with the basic shuffled frog leaping algorithm,the proposed algorithm improves the optimization capability and the success rate greatly.
shuffled frog leaping algorithm,discussion mechanism,dynamically adjusting,optimization capability,success rate
TP301.6
10.3969/j.issn.1672-9722.2017.08.001
2017年3月17日,
2017年4月21日
国家自然科学基金项目(编号:61301108、61671244);中央高校基本科研基金(编号:30915011320)资助。
王俊,男,硕士研究生,研究方向:云计算。徐建中,男,硕士研究生,研究方向:通信安全。徐雷,男,副教授,研究方向:物联网,下一代网络技术,无线网络与移动计算技术,模式识别理论与应用。
