探究万有引力定律的3种特殊应用

王 毅

(保定市第二中学 河北 保定 071000)

探究万有引力定律的3种特殊应用

王 毅

(保定市第二中学 河北 保定 071000)

万有引力定律是高中物理的一个重要规律，虽然教材篇幅较少，却在历年高考中常常作为重点考查内容出现．万有引力定律相关题目充分考查了学生分析问题、建立模型、数形结合、空间想象及应用数学解决物理问题的能力．相关题目还往往与太空探索、最新科技、最受关注的新闻热点及爱国主义教育结合，非常符合高考命题方向．但学生对这部分考题往往不易把握，特别是一些特殊类型的应用学生不知如何入手．

对于万有引力定律的一般应用可以概括为两种，如表1所示.

表1 对万有引力定律的两种应用

这两类问题很常见，学生也比较容易理解，经过一定练习较容易掌握．

而一些特殊类型的应用不能用以上的方法轻易解决，需要调动更多的物理和数学知识以及更深入的逻辑思维能力，往往让学生不知如何入手，成为了很多学生眼中的难题．下面就对万有引力定律的3种特殊类型的应用作一总结归纳．

1 双星和多星问题

双星或多星互相环绕的情景在宇宙中非常常见，也是高考考查重点之一，但由于没有一般应用中的“中心天体”，且万有引力公式中的距离R和向心力公式中的轨道半径r并不相等，导致学生常常答错．

如图1所示，双星问题的几个常用结论：

(1)对两星均大小相等的物理量有万有引力(向心力)、周期、角速度，即

F1=F2T1=T2ω1=ω1

(2)对两星均与质量成反比的物理量有轨道半径、线速度、向心加速度，即

(3)若两星体质量分别为m1和m2，之间的距离为L，则互相环绕的周期为

图1 双星问题

进一步对于多星问题，基本关系是由万有引力的合力提供向心力，同时注意由几何关系确定轨道半径．常见的是三星系统和四星系统，三星系统常见的有两种形式.

形式一为3颗质量相等的星体环绕中心运动，如图2所示.若三星体质量均为m，星体之间的距离为L，则对于任意一个星体核心关系式为

图2 三星成正三角形的系统

形式二为两颗质量相等的星体环绕另一中心星体运动，如图3所示.若两星体质量均为m，中心星体质量为M，轨道半径为r，则对于任意一个环绕星体核心关系式为

图3 三星成直线的系统

对于四星系统，一般为4颗质量相等的星体环绕中心运动，如图4所示.若四星体质量均为m，星体之间的距离为L，则对于任意一个星体核心关系式为

图4 四星成正方形的系统

总之，对于双星和多星问题需要引导学生分析清楚向心力的来源，注意区分星体距离和圆周运动轨道半径的不同，结合运动示意图和几何关系细心求解．

2 椭圆轨道问题

典型应用：如图5所示，卫星a环绕地球匀速圆周运动，轨道半径为r，周期可由万有引力定律求出为Ta，另一卫星b环绕地球做椭圆轨道运动，近地点近似为地球表面，远地点为卫星a轨道处，地球半径为R，求卫星b的周期．则可由开普勒第三定律得出

即可求解．

图5 有卫星做椭圆轨道运动

若问题变形为卫星b的近地点高度为h1，远地点高度为h2，则表达式相应调整为

仍可求解．另外，卫星由远地点运动到近地点所用时间为周期的一半，需要注意的是，椭圆轨道运动与匀速圆周运动不同，前者速率并非保持不变，所以并不是运行任意“半圈”所用时间都为周期的一半．

3 引力势能问题及机械能问题

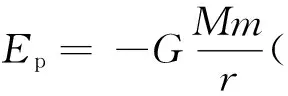
一个典型的应用是：推导第二宇宙速度的表达式．即从地表以某一速度发射物体，其运动到距离地球无穷远处时，速度刚好减为零，把这一速度就称为地球的第二宇宙速度(脱离速度)．由引力势能的概念和机械能守恒定律可列表达式

即在地表发射时的动能和引力势能之和等于飞到无穷远处时的相应能量之和(均为零)．

另外，可以引导学生进一步思考推出环绕中心天体圆周运动的物体的机械能E表达式，即

利用该式可以解决一些本来只能定性理解的问题．例如：某一人造地球卫星原来轨道半径为r1，由于受到外层大气阻力的作用，轨道半径降低为r2，已知地球质量M和卫星质量m及引力常量G，求阻力做功W阻为多少？则利用功能关系和机械能表达式可得

类似题目在多省市高考题中出现，是多数学生解题的难点之一．

以上就是对万有引力定律的3种特殊应用所做的总结，在教学中可以引导学生分析和推导出相应结论，不仅方便应用结论解题，还能锻炼学生的物理思维能力和数学运算技巧．

2017-02-15)