离心泵空化压力脉动特征分析*

贺 国 曹玉良 王小川 明廷锋 苏永生

(海军工程大学管理工程系1) 武汉 430033) (海军工程大学动力工程学院2) 武汉 430033)

离心泵空化压力脉动特征分析*

贺 国1)曹玉良2)王小川2)明廷锋2)苏永生2)

(海军工程大学管理工程系1)武汉 430033) (海军工程大学动力工程学院2)武汉 430033)

为了研究离心泵空化时压力脉动的特征，利用计算流体力学方法对离心泵的空化流场进行了数值模拟，利用傅里叶变换和小波包能量法对泵内压力脉动的特征进行了研究.运用Zwart空化模型和湍流粘度修正后的RNG湍流模型，对离心泵的空化流场进行了稳态数值模拟，得到了离心泵的空化性能，其与实验结果符合良好.对弱空化状态和强空化状态分别进行了瞬态数值模拟，压力脉动的傅里叶分析表明，空化时泵内压力脉动的主频是叶频，由弱空化到强空化，高频部分的谱峰增多、频率成分增加.小波包能量法分析表明，从第1频带(低频带)到第4频带(高频带)，频带的能量先减小再增大，第1频带的能量最大、第3频带的能量最小，由弱空化到强空化，第1频带的能量减小，第3频带的能量明显增加.

离心泵；空化；数值模拟；压力脉动；傅里叶分析；小波包

0 引 言

空化会导致离心泵性能下降，引起泵的振动和噪声，并导致过流部件的腐蚀和破坏[1-2].为了防止离心泵发生空化，必须要弄清离心泵空化时的特征.

数值模拟已成为当前空化流场研究的重要方法之一，很多学者都利用数值模拟方法对空化流场特征和压力脉动特征进行了研究.杨敏官等[3]对一型离心泵进行了空化非定常数值模拟，对泵内压力脉动进行了傅里叶分析，发现压力脉动的幅值随着空化程度的加剧而增大，其中叶频的幅值变化明显.率志君等[4]对多级离心泵内的压力脉动进行了傅里叶分析，发现叶轮和蜗壳内压力脉动的主要频率是叶频及其倍频.王松林等[5]对一型离心泵瞬态空化流动进行了数值模拟，也表明叶轮内压力脉动的主频是叶频，空化流动时各监测点压力脉动的幅值增大.上述研究表明，离心泵空化时压力脉动的主频是叶频，叶频的特征最明显，然而也有学者认为离心泵空化时轴频的特征最明显[6].

小波分析具有较高的时频分辨率，能够提取不同频带的特征，不少学者也利用小波分析对空化流场的特征进行了研究.Ramadevi[7]利用小波包变换对离心泵空化时的振动信号进行分析，发现小波变换能够提取信号的部分特征.De等[8]利用小波分解和神经网络对管道中的空化流动进行了研究，其认为结合这两种方法能够有效地发现空化压力脉动信号的特征.李静等[9]利用小波包变换对水轮机空化超声信号进行了分析.

为了弄清空化时离心泵内压力脉动的特征，本文运用Zwart空化模型和湍流粘度修正后的RNG湍流模型对离心泵的空化流场进行了稳态和瞬态数值模拟，利用傅里叶分析和小波包能量法对隔舌处和出口处的压力脉动进行了研究，分析了泵内压力脉动的频率特征和频带能量特征.

1 空化数值模拟

1.1 离心泵的几何和网格

所用离心泵为单级单吸水泵，其比转速为130，进口直径为126 mm，出口直径为100 mm，叶片数为6片，额定流量为100 m3/h，见图1.

图1 离心泵的几何

运用ICEM软件进行网格划分，所有部件都划分六面体网格，离心泵的口环间隙为0.5 mm，前后腔体及前后口环间隙的网格见图2，叶轮和蜗壳的网格见图3，控制y+小于50，计算域的总网格数为430万.

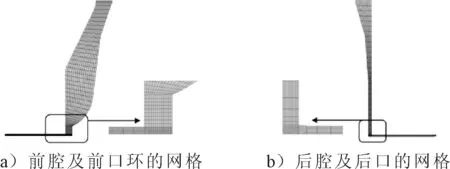
图2 口环间隙的网格

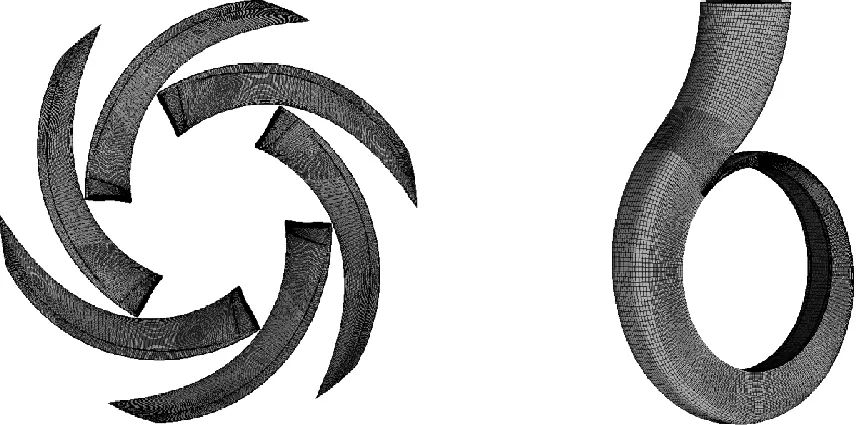
图3 叶轮和蜗壳的网格

1.2 空化模型和湍流模型

空化的数值模拟涉及到空化模型和湍流模型两个方面，在众多的空化模型中，Singhal空化模型和Zwart空化模型应用最广泛[10].本文利用Zwart空化模型对离心泵的空化性能进行数值计算，Zwart空化模型的形式为[11]

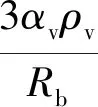
(1)

由文献[12]可知，空化系数为300、凝结系数为0.03.湍流模型采用湍流粘度修正后的RNG湍流模型，湍流粘度的修正方法为[13]

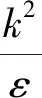
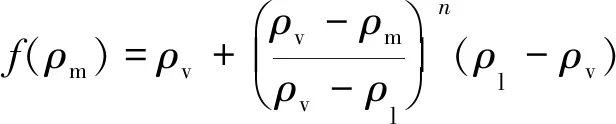
(2)

式中：n为10.考虑湍流脉动压力pturb对汽化压力的影响，饱和压力pv为

(3)

式中：k为湍动能；ρm为混合密度.

1.3 空化性能分析

在进行空化性能数值模拟时，采用流量出口、总压进口，通过不断降低进口的压力使泵内发生空化.流量100 m3/h时的离心泵的扬程与有效汽蚀余量的关系见图4.

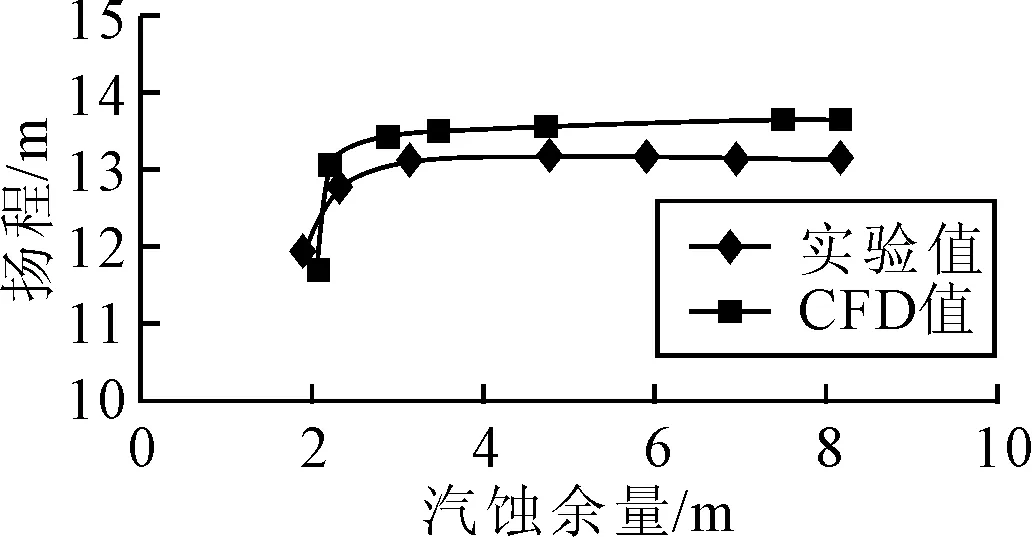
图4 扬程与有效汽蚀余量的关系

由图4可知，CFD数值模拟得出的曲线与实验曲线符合良好，随着汽蚀余量的减小，扬程先缓慢降低，当有效汽蚀余量减小到一定程度后，扬程陡然下降.有效汽蚀余量NPSHa分别为3.45，2.22和2 m时，空泡体积分数为20%的等值面见图5.由图5可知，随着有效汽蚀余量的减小，空泡体积逐渐增大，当有效汽蚀余量从2.22 m减小到2 m时，空泡体积大量增加，由于大量空泡堵塞了过流通道，使叶轮的做功能力降低，导致离心泵的扬程急剧下降.

图5 叶轮上的空泡分布

2 压力脉动的频率特征

2.1 瞬态数值计算

文中对有效汽蚀余量NPSHa=3.45 m的弱空化状态和NPSHa=2.22 m的强空化状态进行了瞬态数值计算，在进行瞬态数值模拟时，离心泵的转速设为1 480 r/min，时间步长取为1.126×10-4s，即叶轮每旋转1°计算一步，每个时间步迭代20次，收敛标准为10-4，总共计算7圈，取后4圈的结果进行分析.

有研究表明，离心泵隔舌处和出口处的压力脉动特征较明显[14]，因此本文也监测蜗舌处(P1点)和出口处(P2点)的压力脉动，P1和P2的位置见图6.

图6 监测点的位置

2.2 频率特征分析

为了能清楚地看出泵内压力脉动的频率特征，将所分析的频带分为0～1 000 Hz和1 000～4 400 Hz两个部分分别显示；为了使频率分辨率保持一致，在进行傅里叶分析时数据点数都取为1 400个，P1点处压力脉动的频率特征见图7.由图7a)可知，在0～1 000 Hz的低频部分，无论是弱空化还是强空化，P1点处压力脉动的最高谱峰都位于叶频(148 Hz)处，除叶频外，还有2倍、3倍、4倍叶频等几个谱峰.由图7b)可知，在1 000～4 400 Hz的高频部分，谱峰的数量增加十分明显，说明从弱空化到强空化，泵内压力脉动的高频成分增多.

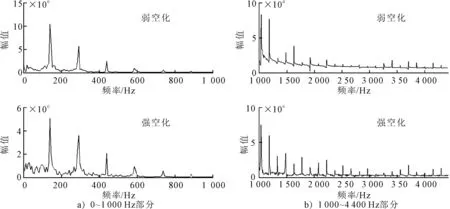
图7 P1点处压力脉动的频率

P2点处压力脉动的频率特征见图8，由图8a)可知，P2点处压力脉动的主要频率也是叶频及其倍频.由图8b)可知，从弱空化到强空化，谱峰数量明显增多，多数谱峰的幅值都有所增大.

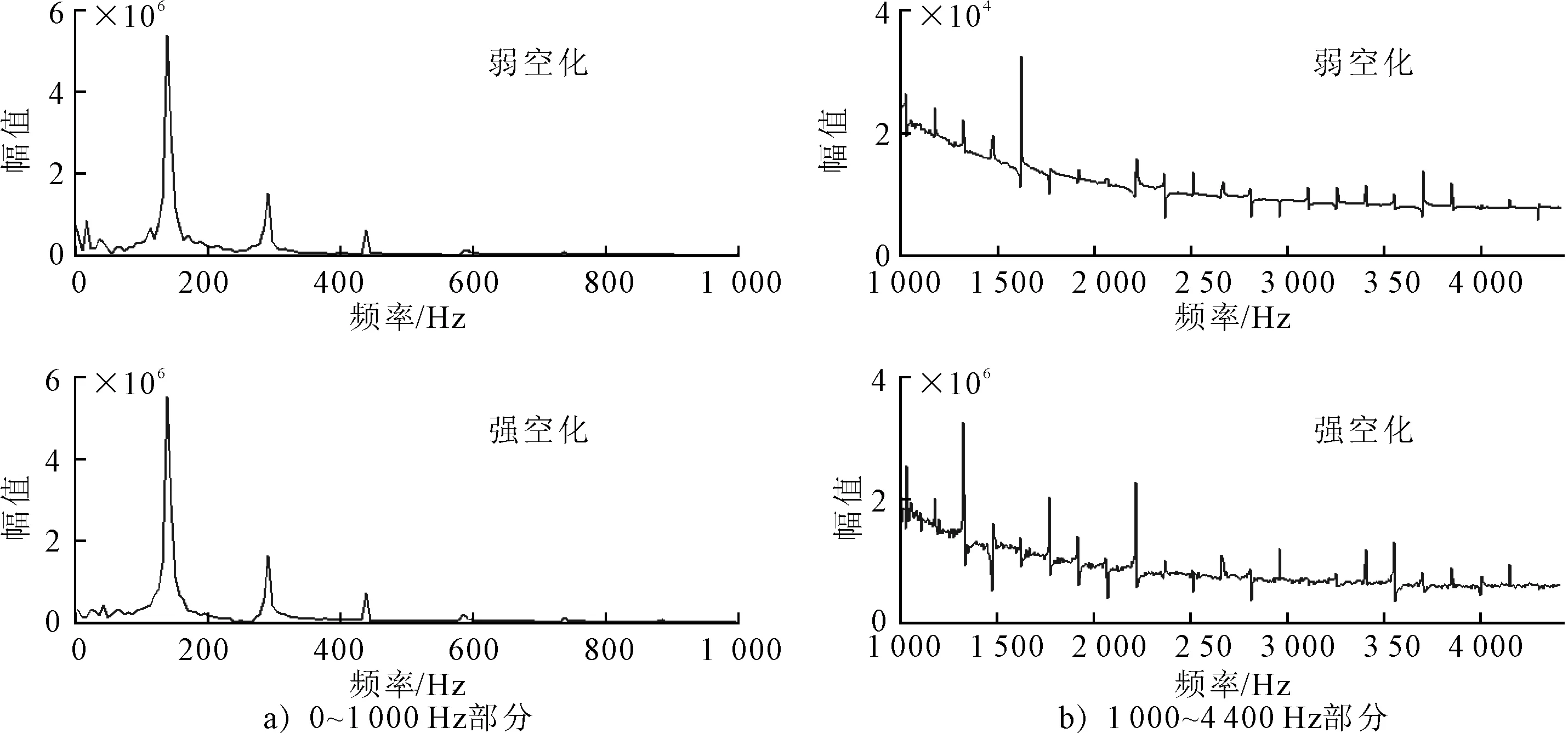
图8 P2点处压力脉动的频率

对比P1点和P2点处压力脉动的频率，发现P1处压力脉动的频率幅值较大，主要是因为叶轮和隔舌的动静干涉，导致隔舌处压力波动剧烈.无论是P1点还是P2点处，由弱空化到强空化，在高频部分都存在谱峰增多和高频频率成分增加的现象，这主要与强空化时泵内空化剧烈、空泡大量溃灭有关.

3 小波包能量法分析

3.1 小波包能量法原理

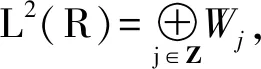
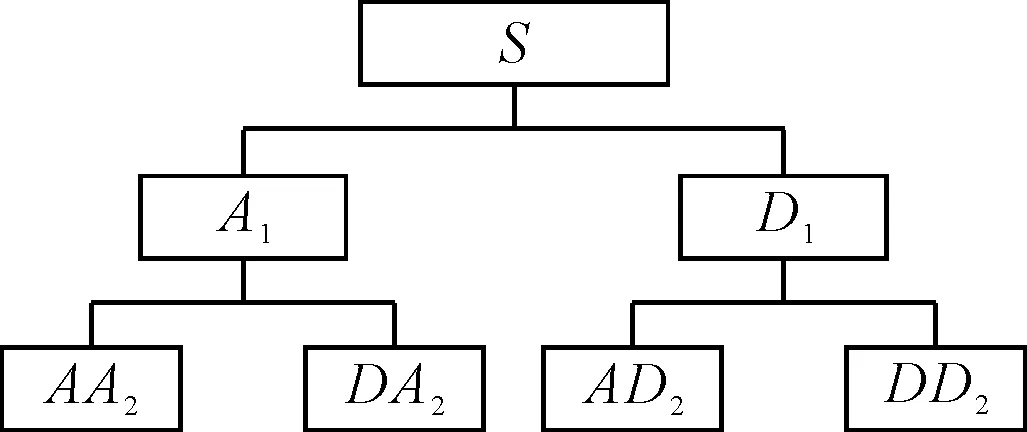
图9 小波包分析的树形结构

小波包分解将信号正交地分解到独立的频带内，每个频带所包含的信息不同，其能量也不同.对于离心泵空化压力脉动而言，空化状态不同，各频带的能量自然也不同，经过小波包分解后各频带的能量表示为

(4)

式中：k为分解层数；n为第k层的第m分频带的信号Sm(i)的长度；n与原信号数据长度N的关系为n=N/2k；第k层频带宽度与采样频率fs的关系为fs/2k.

采用具有正交性、紧支撑性和近似对称性的db6小波对P1和P2点处的压力脉动进行2层分解，得到4个频带，其频带范围分别为0～2 220,2 220～4 440,4 440～6 660,6 660～8 880 Hz，分别求取各频带的能量.

3.2 小波频带能量特征

P1点处压力脉动各频带的能量见图10，其中弱空化时有效汽蚀余量NPSHa=3.45 m，强空化时有效汽蚀余量NPSHa=2.22 m，图中纵坐标为对数坐标.由图10可知，无论是弱空化还是强空化，各频带的能量呈现出相同的变化规律，从第1频带到第4频带，频带的能量先减小再增大，第1频带的能量最大，第3频带的能量最小；从弱空化到强空化，第1频带的能量减小，第2,3,4频带的能量增大，第3频带的能量增幅最明显.

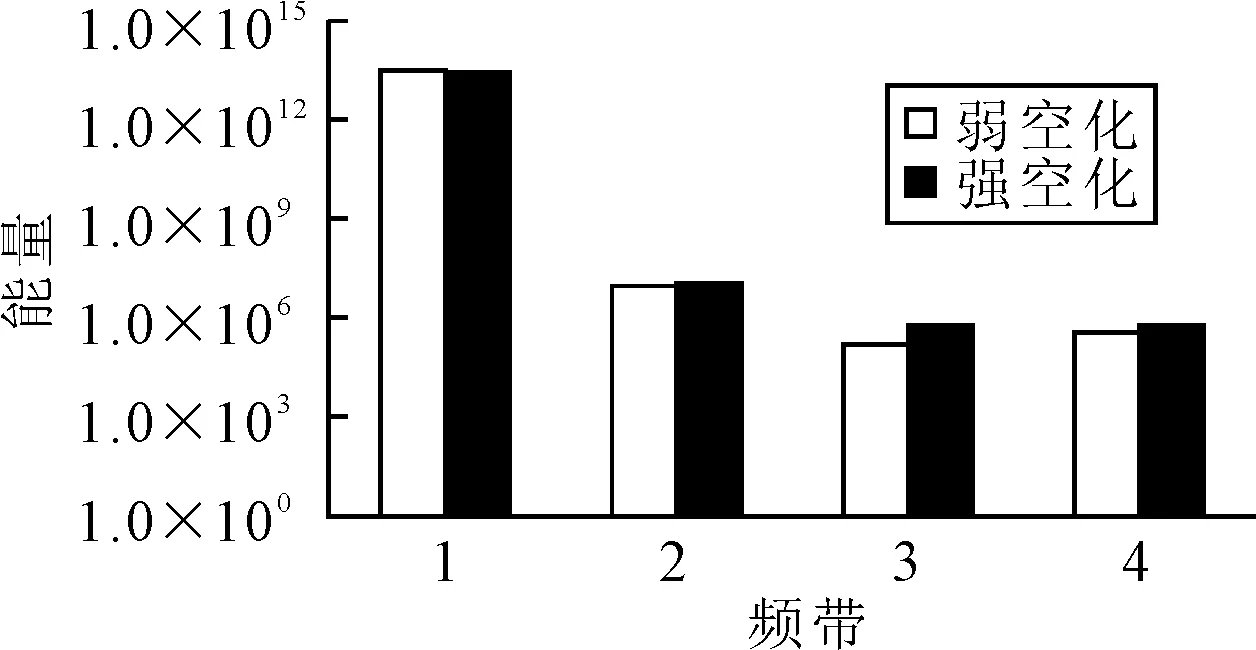
图10 P1点处压力脉动的频带能量

P2点处压力脉动的频带能量见图11，P2点和P1点处压力脉动的频带能量呈现出了相同的变化规律，从第1频带到第4频带，频带的能量也是先减小再增大，第1频带的能量最大，第3频带的能量最小；从弱空化到强空化，第1频带的能量减小，第2,3,4频带的能量增大，表明从弱空化到强空化时，压力脉动的低频能量减小、高频增量增大.与P1点处相比，P2点各频带的能量都稍小一点，其中第2频带的能量减小最明显，说明从隔舌处到泵出口处，第2频带(2 220～4 440 Hz)的能量衰减最快.

图11 P2点处压力脉动的频带能量

4 结 论

1) 数值计算得到了“扬程-有效汽蚀余量”曲线，其与实验曲线符合良好，说明数值计算结果可信.

2) 空化时离心泵内压力脉动的主频是叶频，从弱空化到强空化，高频部分的谱峰增多、频率成分增加.

3) 第1频带的能量最大，从第1频带到第4频带，频带的能量先减小后增大，第3频带的能量最小；从弱空化到强空化，低频带第1频带的能量减小，第2、3、4频带的能量增加，表明压力脉动的低频能量减小、高频增量增大.

[1]JOHANN F G. Centrifugal pumps[M]. Dordrecht: Springer，2014.

[2]KIM K H, J P FRANC, CHAHINE G, et al. Advanced experimental and numerical techniques for cavitation erosion prediction[M]. Dordrecht: Springer,2014.

[3]杨敏官，孙鑫恺，高波，等.离心泵内部非定常空化流动特征的数值分析[J].江苏大学学报，2012，33(4)：408-413.

[4]率志君，张权,陈春来，等.多级离心泵整机流场三维非稳态湍流压力脉动特性分析[J].哈尔滨工程大学学报,2013，34(3):306-310.

[5]王松林，谭磊，王玉川.离心泵瞬态空化流动及压力脉动特性[J].振动与冲击,2013，32(2):168-173.

[6]司乔瑞，袁寿其，李晓俊，等.空化条件下离心泵泵腔内不稳定流动数值分析[J].农业机械学报，2014，45(5)：84-90.

[7]RAMADEVI R. Cavitation signal analysis using discrete wavelet transform[C]. International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT),2014.

[8]DE GIORGI M G, FICARELLA A, LAYEKUAKILLE A. Cavitation regime detection by LS-SVM and ANN with wavelet decomposition based on pressure sensor signals[J]. IEEE Sensors Journal,2015,15(10):5701-5708.

[9]李静，周建中，肖剑，等.基于小波包变换和关联维数的空化信号特征提取[J].水力发电，2013，39(10)：53-57.

[10]曹玉良，贺国，明廷锋，等.水泵空化数值模拟研究进展[J].武汉理工大学学报(交通科学与工程版)，2016，40(1)：55-59.

[11]ZWART P J, GERBER A G, BELAMRI T. A two-phase model for predicting cavitation dynamics[C]. Fifth International Conference on Multiphase Flow, Japan, Yokohama,2004.

[12]MITJA M, ENRICO N, IGNACIJO B. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil[J]. International Journal of Multiphase Flow,2011,37:620-626.

[13]SINGHAL A K, ATHAVALE M M. Mathematical basis and validation of the full cavitation model[J]. Journal of Fluids Engineering,2002,124:617-624.

[14]汪洋，代翠.离心泵内部不稳定流场压力脉动特性分析[J].农业机械学报，2010，41(3)：91-95.

Characteristic Analysis of Cavitation Pressure Fluctuation in Centrifugal Pump

HE Guo1)CAO Yuliang2)WANG Xiaochuan2)MING Tingfeng2)SU Yongsheng2)

(DepartmentofManagementScience,NavalUniversityofEngineering,Wuhan430033,China)1)(CollegeofPowerEngineering,NavalUniversityofEngineering,Wuhan430033,China)2)

In order to study the characteristic of pressure fluctuation in centrifugal pump, the cavitation flow in centrifugal pump is numerically simulated by Computational Fluid Dynamics (CFD) method, and the characteristics of cavitation pressure fluctuation are studied by Fourier analysis and wavelet packet energy method. Firstly, by using Zwart cavitation model and turbulent viscosity modified RNG turbulent model, the cavitation flow in centrifugal pump is numerically simulated steadily, and the cavitation performance is obtained, which matched well with the experimental results. Secondly, the slight cavitation situation and heavy cavitation situation are numerically simulated transiently. The Fourier analysis of pressure fluctuation demonstrates that the main frequency of cavitation pressure fluctuation in the pump is blade frequency. From slight cavitation to heavy cavitation, the quantity of spectral peaks and frequency elements in high frequency band increase. The analysis of wavelet packet energy method demonstrates that the energy of bands decrease firstly and then increase from 1st band (low frequency band) to 4th band (high frequency band). The energy of 1st band is the highest and the energy of 3rd band is the lowest. From slight cavitation to heavy cavitation, the energy of 1st band decrease, and the energy of 3rd band increase greatly.

centrifugal pump; cavitation; numerical simulation; pressure fluctuation; Fourier analysis; wavelet packet

2017-06-15

*国家自然科学基金项目(51306205，51609250)、湖北省自然科学基金项目(2015CFB700)、海军工程大学博士生创新基金项目(4142C15K)资助

U664.33

10.3963/j.issn.2095-3844.2017.04.003

贺国(1965—)：男，教授，博士生导师，主要研究领域为状态与故障诊断