改进投影数据访问顺序的CT图像重建研究

张蕾+徐伯庆

摘 要：代数重建算法是CT图像重建中较为常用的图像重建算法，重建图像的质量和速度是评价重建算法优劣的两个重要标准。传统的代数重建算法有重建质量低、速度慢的缺点。针对这些缺点，提出了一种改进投影数据访问顺序的代数重建算法。该算法通过对投影访问顺序的选择，减小了投影数据间的相关性，同时保证了投影角度的均匀分布，避免了密集访问情况的出现。实验结果证明，采用改进的算法进行CT图像重建不仅能减少图像伪影，而且能很好地改善重建图像质量，明显加快重建速度。

关键词：CT图像重建；代数重建；投影数据；访问顺序；最小相关性

DOIDOI：10.11907/rjdk.171337

中图分类号：TP317.4

文献标识码：A 文章编号文章编号：1672-7800（2017）008-0189-04

0 引言

计算机断层成像（Computed Tomography， CT）技术从外部测量物体得到数据重建内部信息，普遍应用于医学、无损检测等领域[1]。代数重建法（ART）和滤波反投影法（FBP）是CT图像重建的两类经典算法[2]。FBP算法重建的圖像质量好且速度快，但其条件是有充足的投影数据，而现实操作中却很难做到。ART算法不需要这一条件，但其重建速度会减慢[3]。将现实问题转化为运用代数方式解线性方程组的数学问题是ART算法的核心思想[4]。初值选取、投影数据访问顺序、松弛参数选择等因素对重建过程都有不同程度的影响[5-7]。其中，投影数据访问顺序对重建速度和质量影响较大。为此，学者进行了大量研究，如固定角度访问顺序、Van Dijke[8]提出的随机访问顺序等。通过深入分析与研究，本文提出一种基于改进投影数据访问顺序的ART算法，以求改善CT图像重建的精度和速率。

1 ART算法原理

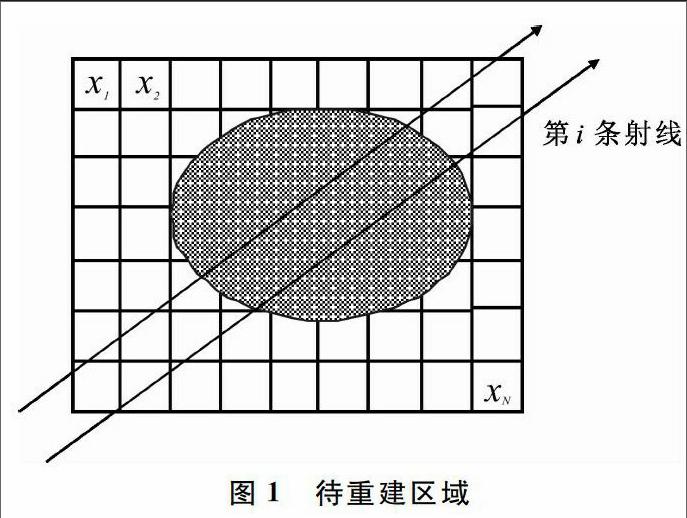
ART算法首先将被重建的物体离散化为一个个像素或体素，这些图像数据就相当于一个未知的数学矩阵，通过不同投影角度获取的投影数据联合这一未知的数学矩阵建立线性方程组，用迭代的方式求解方程组便可得到原始图像矩阵[9]。本文以二维图像为例，将待重建图像离散化为N=m×n个图像像素，待重建区域划分为一个个网格，并用xi（1≤i≤N）表示第i个网格内像素的平均值，如图1所示。

在此，采用平行束投影方式进行数据采集。平行射线的总数为M，图像像素的总数为N，待重建区域由N个边长为1的正方形网格组成。按照CT图像重建原理以及构造的数学模型，投影数据与像素值之间的关系可用下式表示：

W11x1+W12x2+…+W1NxN=p1W21x1+W22x2+…+W2NxN=p2…WM1x1+WM2x2+…+WMNxN=pM （1）

式（1）中，Wij为权重因子，即第i条射线对第j个像素的奉献值，pi（1≤i≤M）为待重建图像在第i条射线上的投影值，即待重建图像沿此射线方向的线积分。由于M、N的值通常都很大，且每条射线与像素的交点个数较少，权重因子矩阵成为大型稀疏矩阵，所以只能采用迭代方式求解。

ART 算法通过对未知图像矩阵赋初值，再将射线扫描图像得到的实际投影数据与估计的投影数据进行比较，使用迭代公式对初值进行校正与更改，便可完成第一次迭代。若一次迭代后未满足收敛条件，则将更新后的图像矩阵作为下一次的初值，继续以上步骤直至达到收敛条件[10]。ART算法的迭代公式如下：

x（n + 1）j = x（n）j + λWij ∑Nj = 1W2ij pi -∑Nj = 1Wij x（n）j（2）

式（2）中，n为迭代次数，λ为松弛参数（0<λ<2），且i=1，2，…，M，j=1，2，…，N。

2 投影数据访问顺序改进

2.1 最小相关性原理

将方程组（1）中的M个方程抽象化为N维空间内的M个超平面，若方程组的解只有一个，M个超平面的交点便是其解。若M>N，方程组便不会有唯一解，超平面的交点附近会产生震荡；若M

初始值设为x0，将x0投影至第一个超平面，再将得到的值垂直投影至第二个超平面，反复操作直至达到两个超平面的交点。从图2得出结论：到达交点需要的迭代次数随着夹角的增大而减少。若超平面的夹角为直角，迭代2次便可完成。同时，超平面的夹角较大时，可获得较高精度的最终解。因此，为了达到收敛速度快、重建质量好的目的，需要对投影数据的访问顺序进行选择，增大相邻超平面间的夹角，减小数据相关性，这就是最小相关性原理。选择高效的投影数据访问顺序可在迭代初期较快重建高频成分[12-14]。这一高效的投影数据访问顺序除了需要满足最小相关性原理外，还需要遵循以下原则：①在视角范围内，投影角度应尽可能分布均匀；②不允许投影角度在某些角度被密集访问。

2.2 改进的投影数据访问顺序

改进的投影数据访问顺序充分运用最小相关性原理，而且投影角度均匀分布，未出现投影角度密集访问情况。假设投影角度范围为[0，θ]，采用间隔为α的均匀采样，投影数据访问顺序改进步骤如下：①设i=0为首个投影角度；②投影角度按以下循环体选择：j=i，j<θ，j=j+90；③i=i+α，重复步骤②，直至遍历所有投影角度。通过以上方式选择的投影数据访问顺序，使得相邻射线间的夹角尽量满足90°，从而减小射线穿过像素的信息相关性。如θ=360，α=3时，按照以上步骤可得投影数据的访问顺序为：0，90，180，270，360，3，93，183，273，…。

3 實验结果与分析

3.1 图像质量评价方式

图像质量的好坏可用主观和客观两种方式评价。主观评价就是通过人眼进行直观判断，这种方式虽然直观可见，但容易受到人的主观影响，缺乏科学依据。客观评价就是通过计算机模拟计算出图像的各项衡量指标，结合原始图像和重建图像的匹配程度来评价。为了直观对比，本文综合这两种方式来评估图像质量，并采用以下3项指标作为客观评价标准：（1）密度曲线对比图，即根据图像的某一列或某一行的像素值绘制密度曲线图，对比分析重建图像与原始图像像素的偏离大小，直观判断重建算法的优劣。（2）峰值信噪比PSNR，设xi 表示重建后图像的像素值，其均方误差MSE可表示为：

MSE = 1M×N∑0≤i < N（xi -xi ）2（3）则峰值信噪比PSNR可表示为： PSNR=10lg255×255MSE（4）由式（4）可知，PSNR的值越大，重建图像中的噪声越小，重建的质量越好。（3）归一化平均绝对距离r，计算公式如下： r = ∑0≤i < Nxi -xi ∑0≤i < Nxi （5）由式（5）可知，r值越小，图像失真越小，重建效果越好。

3.2 实验结果与分析

为了验证改进算法的正确性与可行性，选用集算法研究、建模仿真、可视化、数据分析等功能为一体的MATALB仿真软件进行仿真实验。实验采用Sheep-Logan头部模型切片来模拟分析不同投影数据访问顺序对CT图像重建的影响。该头部模型是CT图像重建领域内的经典仿真模型，像素取值范围为[0，255]，实验采用的模型大小为128×128。

实验采用4种算法分别在无噪声条件下进行图像重建，投影数据访问顺序各不相同，分别为：顺序访问（SAR）、随机访问（RAS）、固定角度访问（FAS）、改进的投影数据访问（PAS），其中FAS采用的固定角度为67°。实验中的投影射线均为平行束投影，投影角度取值范围为[0，180°]，均匀采样间隔为1°，即投影射线每间隔1°扫描一次，185条投影射线平均分布在每个投影角度上，因此获得的投影矩阵大小为185×180。图像的初值为0，松弛参数为1，迭代次数为6次，图3为4种访问方式重建的图像，图4为在x=64即垂直方向上各个重建图像的像素值图。

由图3可以看出4种不同访问顺序的ART算法均能成功重建图像，但都有一定条状伪影。从图像可以看出，采用改进的投影数据访问顺序重建出的图像较之其它3种方式重建的图像愈发清晰，伪影较少。由图4可以发现，基于这4种不同访问顺序得到的重建图像像素值较之原始图像像素值差别均不大，但是采用改进的投影数据访问顺序的密度曲线与原始图像更为接近，误差最小。

为了更加客观地分析对比图像重建的质量和速度，不断增加迭代次数，观察随着迭代次数的增加，采用不同访问顺序重建图像的值和值的变化。图5所示为随着迭代次数的增加两种评价标准的变化曲线，其中（a）为PSNR值变化曲线、（b）为r值变化曲线。由图5可知，改进的投影数据访问顺序重建的图像PSNR值最大，r值最小，即图像重建质量最好。随着迭代次数增加，收敛速度也越快，最终迭代6次后，改进的CT图像重建算法趋于稳定，且重建图像质量始终优于其它访问顺序的算法。

使用MATLAB仿真软件记录程序运行时间t，进一步评价各种算法效率。表1所示为迭代6次时，不同投影数据访问顺序评价标准值。由表1可以看出，在迭代6次时，本文算法得到的重建图像误差最小，质量最好，同时运行时间最短。以上各项实验数据和仿真图像，充分证实了改进的算法不但提高了图像的重建质量，还实现了重建算法的快速收敛。

4 结语

CT图像重建影响因素众多，本文对投影数据的访问顺序作了改进。对实验结果分析发现，投影数据的访问顺序直接决定着图像质量的优劣和重建速度的快慢。本文提出的投影数据访问顺序不仅在视角范围内均匀分布且不密集出现，而且满足了最小相关原理，使得连续投影射线间的投影数据相关性最小。改进算法不仅大大提高了重建质量，而且明显加快了重建速度。本文的仿真实验均在无噪声条件下进行，但实际环境中CT扫描难免受到噪声污染，今后将进一步研究在有噪声情况下CT图像重建算法的改进，使其更好地应用到实际场景中。

参考文献：

[1] HERMAN G T.Image reconstruction from projections[M].London：ACADADEMIC P-RESS， 1980.

[2] 徐国良，陈冲，李明.图像重构的数值方法[M].北京：科学出版社，2015.

[3] 庄天戈.CT原理与算法[M].上海：上海交通大学出版社，1992.

[4] NATTERER F.The mathematics of computerized tomography[M].Society for Industrial Mathematics， 2001.

[5] 杨文良，魏东波.一种改进投影系数计算的快速ART算法[J].CT理论与应用研究，2012， 21（2）： 187-195.

[6] GUAN H，GORDON R.A projection access order for speedy convergence of ART：a multilevel scheme for computed tomography[J]. Physics in Medicine and Biology， 1994， 39（11）： 2005-2022.

[7] HERMAN G， MEYER L. Algebraic reconstruction can be made computationally efficient[J]. IEEE Trans， Med Img，1993， 12（3）： 600-609.endprint

[8] VAN DIJKE.Iterative methods in image reconstruction[M]. The Netherlands， 1992.

[9] KESIDIS A L，PAPAMARKOS N.Exact image reconstruction from a limited number of projections[J]. Journal of Visual Communication and Image Reconstruction， 2008， 19（5）： 285-298.

[10] 李志鹏，丛鹏，邬海峰.代数迭代算法进行CT图像重建的研究[J].核電子学与探测技术，2005，25（2）： 184-186.

[11] MAN B D. Statistics methods for image reconstruction part 3： x-ray computed tomography[C]. IEEE Nuclear Science Symposium and Medical Imaging Conference， Honollu， 2007.

[12] 王宏钧，路宏年，傅建.代数重建技术中投影序列选择次序的研究[J].光学技术，2006，32（3）： 1005-1022.

[13] THIBAULT JB， SAUER KD， BOUMAN CA， et al. A three-dimensional statistical approach to improve image quality for multislice helical CT[J]. Medical Physics， 2007， 34（11）： 4526-4544.

[14] MUELLER K， YAGEL R， CORNHILL J F. The weighted distance scheme： a globally optimizing projection ordering method for the algebraic reconstruction technique （ART） [J]. IEEE Transaction on Medical Image， 1997， 16（2）： 223-230.endprint