基于复合置乱算法的数字图像加密系统设计与实现

孔军辉+赵冬梅+宋阳

摘 要：分析了目前比较流行的Arnold 算法和骑士巡游算法各自的特点，利用两种算法之间的互补性，设计了基于Arnold变换和骑士巡游变换相结合的复合置乱算法，并对数字图像进行加密。该设计以Altera公司的NIOSⅡ嵌入式软核处理器为核心，创建了用户自己的数字图像处理芯片。

关键词：Arnold 算法；骑士巡游算法；复合置乱；图像加密

DOIDOI：10.11907/rjdk.171332

中图分类号：TP309.7

文献标识码：A 文章编号文章编号：1672-7800（2017）008-0179-03

0 引言

随着网络和多媒体技术的发展及应用，以数字图像信号为主要载体的数据应用已逐渐成为人们生活的主旋律。它虽然给人们生活带来了便利，但同时也存在着安全隐患。据统计，全世界几乎每20s就会发生黑客入侵事件。不法者经常会在数字图像信号传输或存储过程中窃取信息。因此，保护这些图像信息的安全尤为重要。目前，对数字图像进行加密处理是解决这类问题的主要手段之一[1]。

1 加密算法选择

对数字图像进行隐藏和伪装有很多种算法，主要有数字图像置乱技术、数字图像信息隐藏技术、数字图像水印技术和数字图像分存技术[2]。本文采用的是数字图像置乱技术，这种技术主要利用数字图像的矩阵性，对图像中像素的位置或颜色进行扰乱，从而解决数字图像的安全问题。目前，比较流行的置乱技术有Arnold置乱算法和骑士巡游置乱算法。

1.1 Arnold置乱算法

Arnold 变换是在遍历理论研究中提出的一种变换，俗称猫脸变换[3]，具体变换公式如式（1）。 定义：设有单位正方形上的点（ x，y ），将点（ x，y） 变到另一点（ x′，y′）的变换为：

x′y′=1 11 2xy（mod1）

（1）

由式（1）可知，Arnold 变换实际上就是将数字图像中代表像素的颜色值或灰度值的坐标点进行位置移动的过程，虽然一次移动不能解决问题，但一直重复下去，每一次的最后输出作为下一次的输入，经过N次迭代后，就会出现无法辨认的图像。值得注意的是，随着迭代次数的增加，迭代到一定数值后数字图像就会被还原，这说明Arnold变换具有一定的周期性，合理利用此特点，可以帮助人们完成数字图像的解密工作。

1.2 骑士巡游算法

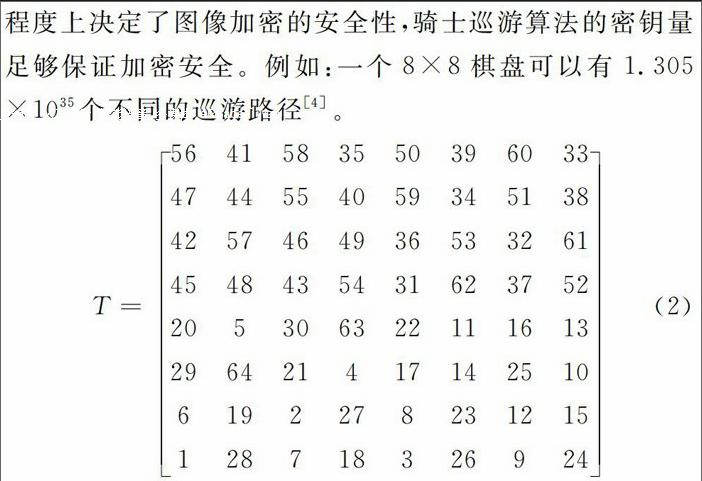
骑士巡游算法，就是让一个骑士从数字图像上任意一点像素出发，按照国际象棋“日”字的规则走动，走动过程中要求骑士不重复地走遍n×m棋盘上的每个小方格。骑士巡游路径不是唯一的，可以用矩阵来表示，此矩阵称为巡游矩阵。例如在一个8×8的棋盘中，一个骑士从起点1出发，按照式（2）所示矩阵规则进行巡游，直到走完矩阵中的每一点。可以看出，这种算法的密钥就是巡游矩阵，路径的数量就是加密的密钥量。密钥量的数量在一定程度上决定了图像加密的安全性，骑士巡游算法的密钥量足够保证加密安全。例如：一个8×8棋盘可以有1.305×1035个不同的巡游路径[4]。

1.3 复合置乱算法

综上可知，Arnold变换和骑士巡游变换在对数字图像进行加密处理上有着各自的特点。Arnold变换处理速度快，短时间内置乱效果好，但密钥量小、安全性不高。骑士巡游算法密钥量大、安全性高，但速度慢，适合对细节的处理。由于两种算法之间具有很强的互补性，因此本次设计选择基于Arnold变换和骑士巡游变换相结合的复合置乱算法，这样可以做到扬长避短，对数字图像有着更好的加密效果。

2 系统硬件设计

本文采用嵌入式系统SOPC作为图像加密的硬件平台，以美國Altera公司Nios II软核处理器为核心，对数字图像进行加密设计。外界影像首先通过传感器转换为符合CCIR656 协议的图像信号，再通过EP2C35开发板上的I/O接口，以DMA方式存储在SDRAM 中，等待Flash 中的加密程序对其处理。加密后的图像数据通过液晶屏接口程序，由数字液晶屏接收并进行显示。具体过程如图1所示。

3 系统软件设计

软件设计的主要任务是对存储在SDRAM中的图像数据进行加密处理。首先为了防止在读取图像数据时发生冲突，要在SDRAM 中申请一个用来采集输入，一个用来显示输出的两个帧缓存区（640×480×2×8=4.915 2M帧）。当图像数据读入后，由保存在Nios II 软核处理器中的加密算法对其进行加密，接到输出指令后，进行输出，在液晶屏上显示密图。整个过程只要有图像数据输入就会不断进行下去。

在Nios II IDE下编辑的基于Arnold变换和骑士巡游变换相结合的复合置乱算法关键加密代码如下：

void Arntranst（int m-Times） //Arnold 变换置乱函数

{

……//变量定义及赋值过程

for（k=1；k<=_Times；k++）

{ for（i=0； i

{ for（j=0；j

{ IpSrc = （uint8*）p_data+wide*i+j； //IpSrc为源位图中待加密象素指针

//P_data为指向源位图数据区首象素的指针

m=i+j；

n=i+2*j；

if（m>=wide）

m=m%wide；

if（n>=height）

n=n%height；

IpDst=（uint8 *）temp+wide*m+n；

//IpDst 为IpSrc 所指向的象素经过复合置乱算法映射后在缓冲区中的指针

*IpDst=*IpSrc；}}

memcpy（p_data，temp，wide*height）；}}

void Knight8（int m_Times1） //8*8騎士巡游置乱函数

{

……//变量定义及赋值过程

for （ k=1；k<=m_Times1；k++）

{ for （m=0；m

{ for（n=0；n

{ x=8*m；

y=8*n；

for （i=x；i

{ for （j=y； j

{ u=findrow（T，64）；

v=findcolum（T，64）；

x1=x+u；

y1=y+v；

*（uint8*）（temp+i*wide+j）=*（uint8*）（p_data+x1*wide+y1）

} } } }

memcpy（p_data，temp，wide*height）； }}

4 实验比较

由于受目标板存储空间的限制，本次加密只是针对256×256像素的8位灰度图进行实验，实验通过改变迭带值进行几种置乱技术加密效果的比较。图2是对原始图像分别进行0、1、5、8、10次Arnold 算法的实验结果，图3是对原始图像进行0、2、5、8、48次骑士巡游算法的实验结果，图4是对原始图像进行0+0、1+2、5+5、8+8、10+48次复合算法的实验结果。

从实验效果可以看出，基于Arnold变换和骑士巡游变换相结合的复合置乱算法对图像加密效果良好。

5 结语

本文将Arnold变换和骑士巡游变换相结合，提出一

种新的复合图像置乱加密算法，并用目标板实现了相应的功能。在设计过程中将3种置乱算法在加密效果上进行了分析比较，结果表明，复合置乱算法无论在加密效果上还是在安全性上都得到了很大提升。但也存在一些问题亟待解决，例如彩色图像加密、图像解密的复杂性等问题，都有待进一步研究。

参考文献：

[1] 张志刚.FPGA与SOPC设计教程[M].西安：电子科技大学出版社，2007.

[2] 王丽娜.网络多媒体信息安全保密技术[M].武汉：武汉大学出版社，2003.

[3] 邹建成，铁小匀.数字图像的二维 Arnold 变换及其周期性[J].北方工业大学学报，2000（1）：10-14.

[4] GL CHIA，SIEW-HUI ONG.Generalized knight's tours on rectangular chessboards[J].Discrete Applied Mathematics，2005（5）：80-98.

[5] 王建校，危建国.SOPC基础与实践[M].西安：电子科技大学出版社，2006.