基于BP神经网络的太阳能收集功率预测研究

李玲生+韩崇

摘 要：在太阳能收集应用系统中，能量收集预测模块是进行合理的任务调度分配和系统平稳运行的重要保证。提出了基于BP神经网络的太阳能收集功率预测方法，优化了算法的参数选择，确定了算法预测性能指标。在真实太阳能收集功率数据集上对提出的算法进行了性能分析，验证了算法参数选择的正确性；与现有其它数据预测算法进行了一系列预测对比实验。实验结果表明，该预测算法具有良好的性能，在各算法预测性能指标上均具有一定优势。

关键词：太阳能；能量收集；BP神经网络；数据预测

DOIDOI：10.11907/rjdk.172153

中图分类号：TP319

文献标识码：A 文章编号文章编号：1672-7800（2017）008-0138-05

0 引言

太阳能是一种清洁能源，太阳能的利用主要是通过光电和光热等转换技术，将太阳能转换成可集中利用和储存的能源。太阳能是一种可再生能源，它资源丰富，对环境污染较小，特别是在当前能源储备受限，能源竞争压力大、环境污染形势严峻的背景下，研究太阳能的采集和应用具有重要意义[1]。随着太阳能光伏发电相关技术的快速发展，当前太阳能收集技术已经取得了长足进展，太阳能的利用也日趋成熟。这些采集到的能量大到可以提供电网系统电力供应，小到可以提供无线传感器和微机电系统等的能量供给[2-3]。以太阳能收集技术在无线传感器网络中的应用为例，传感器节点配备太阳能收集器，如光伏太阳能板，进行太阳能的收集，然后将收集的太阳能转化为电池存储在传感器节点能量缓冲器中，如可充电锂电池，然后在传感器节点的能量管理模块控制下，进行节点工作的能量供应[4]。

从无线传感器网络方面而言，无线传感器网络是由部署在监测区域内的大量传感器以自组织和多跳等方式构成的，以协作方式感知、采集、处理和传输网络覆盖区域内监测对象信息的无线网络[5]，通过无线传感器网络与因特网的高效融合，可以实现人与物、物与物的互联，从而形成“物联网”[6]。无线传感器网络所感知的数据是物联网海量信息的重要来源[7]。无线传感器网络将在军事国防、工农业控制、城市管理、生物医疗等领域有广阔的应用前景，并且取得了一定的应用成果。然而无线传感器网络在实际应用中同样面临许多挑战，仍旧难以达到普遍应用，其根本原因之一就是传感器节点的有限能量供应问题。当前很多应用场所出于地形复杂或环境恶劣等因素，传感器节点是通过有限电池进行供电，采用更换电池的方法实现能量补给较难，这严重制约了传感器节点的生命时间，降低了整个生命周期。为了降低整个网络的能耗、延长无线传感器网络寿命，相关节能措施被探讨研究，例如研究各种能量有效的通信路由协议，设计周期性工作/休眠的低占空比及工作调度方式等，但是这些措施仅仅从能耗的角度达到节能效果，因此不能从根本上解决受限的电池能量问题[8]。环境能量收集技术，特别是太阳能收集技术，才是解决传感器网络节点能耗问题的根本有效技术，因而得到了研究者们的关注，是当前的一个研究热点[9-10]。

在太阳能收集利用系统中，能量预测模块至关重要。在传感器网络中，节点需要根据预测到的太阳能进行节点的功率控制，若预测接下来收到的能量较少，就要降低节点功耗，进行休眠调度等，反之，则可以增大节点工作功率，完成更好质量的节点监测。传感器节点功率管理是基于将要收集到的太阳能的预测之上，整个系统运行的稳定性很大部分上就是依赖于该能量预测模块[11-12]。如果将来预测的能量大于收获能量，则传感器节点的电源将不足以支持预期的功能，导致节点能量过早耗尽，造成网络意外中断。如果预测值小于收获值，则当达到储能限度时，会浪费超出能量。

本文主要研究太阳能收集功率的预测问题。太阳能具有规律性和不规则性的混合特征：一方面，随着太阳每天的升起和落下，太阳辐射每天都以脉冲的形式发生；另一方面，随着天气和时间的变化，接收到的太阳能在地球上的一天和跨天有显著变化。現有的太阳能预测方法中，比较典型的有EWMA[13]和WCMA[14]，主要是通过对历史采集数据分析，预测未来短期的采集量。在天气平稳的地区，已经可以将预测误差控制在很小的范围内，特别是WCMA能够适应天气的简单变化，但天气发生大的变化时，上述算法则很难保证预测的准确性。本文提出采用BP神经网络方法进行太阳能收集功率的预测。通过采用公用真实太阳能收集功率数据集[15]，对BP神经网络方法进行参数修正，用于新数据的预测，提高预测效率。

1 BP神经网络方法概述

神经网络方法是从神经心理学和认知科学研究成果出发，应用数学方法发展起来的一种具有高度并行计算能力、自学能力和容错能力的处理方法。神经网络的结构由一个输入层、若干个中间隐含层和一个输出层组成。神经网络分析法通过不断学习，能够从未知模式的大量复杂数据中发现其规律。神经网络方法克服了传统分析过程的复杂性及选择适当模型函数形式的困难，是一种自然的非线性建模过程，不需分清存在何种非线性关系，给建模与分析带来极大方便[16]，数据预测是其一个重要的应用方向。BP（Back Propagation）算法又称为误差反向传播算法，是人工神经网络中的一种监督式学习算法。BP神经网络算法在理论上可以逼近任意函数，基本结构由非线性变化单元组成，具有很强的非线性映射能力。而且网络的中间层数、各层的处理单元数及网络的学习系数等参数可根据具体情况设定，灵活性很大。因此，BP神经网络方法是一种典型的神经网络模型[17]。

BP神经网络算法包含两个过程：信号的前向传播和误差的反向传播。即当传入输入信号通过隐含层作用于输出节点，经过非线性变换产生输出信号。如果输出值与期望值不相等，则转入反向传播过程。将输出值与真实值之间的差通过隐含层向输入层逐级反传，并且将误差分摊在各个单元，各层单元依次来调整个单元的权值，从而使误差越来越趋于零。endprint

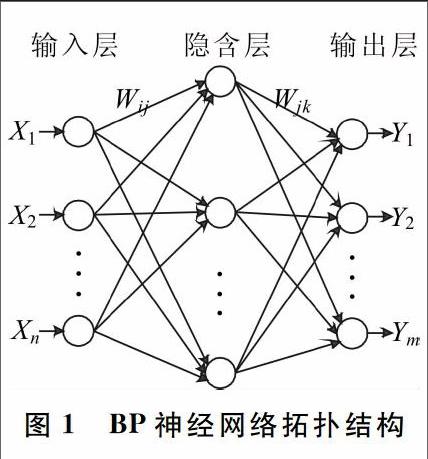
如图1所示，BP神经网络组成如下：①第一层是输入层：作用是接收外部环境的输入信号，并由它传递给相连的隐含层上的各个神经元；②第二层是隐含层：是神经网络的内部處理层，神经网络所具有的模式变换能力主要在隐含层的神经元上，即作用是处理内部中的信息变换；③第三层是输出层：是用于产生神经网络的输出模式，通过输出层将隐含层内部计算出来的信息输出。

在图1中，Xi指输出层的第i个自变量，即样本中自变量向量的第i个值；Wij为BP神经网络中输入层与隐含层之间的连接权值；Wjk为隐含层与输出层之间的连接权值；Yi为输出层第i个神经元的输出值。其中i、j的取值为1，2…，n。由图1可知，BP神经网络是一个非线性的函数，输入值和输出值可分别看作函数的自变量和因变量。当输入的节点为n，输出的节点为m时，就变成了一个n到m的映射过程。神经网络的建模过程中需要大量的数据进行测试，在本文的模型应用中，例如选择2008-2017年每年4月份每天12点收集的太阳能的数据共300条。前270条（2008-2016年每年4月份）数据作为训练测试数据，后30条（2017年4月份）数据作为期望数据。若想利用BP神经网络进行预测，则需要先对前9年的数据进行学习。在神经网络中，学习规则就是修正权值的一种算法，其目的是让神经网络的输出更符合实际值。具体而言，BP神经网络的训练步骤如下：步骤1：网络初始化。根据系统输入输出序列（X， Y）确定网络输入层节点数n、隐含层节点数m、输出层节点数l，以及初始化权值与阈值Wij、Wjk，给定神经元的激活函数给定计算精度值p或最大学习次数N。步骤2：隐含层的输出计算：

Hj=f（∑ni=1WijXj-aj），j=1，2，…，l（1）

步骤3：输出层的输出计算：

f（x）=11+e-x（2）

步骤4：误差计算：

Ok=∑lj=1HjWjk-bk，k=1，2，…，m（3）

步骤5：权值更新：

ek=Yk-Ok，k=1，2，…，m（4）

步骤6：阈值更新：

Wij=Wij+ηHj（1-Hj）x（i）∑mk=1Wjkek，i=1，2，…，n；j=1，2，…，lWjk=Wjk+ηHjek，j=1，2，…，l；k=1，2，…，m（5）

步骤7：判断迭代过程是否结束，若没有则需返回步骤2进行继续迭代。

aj=aj+ηHj（1-Hj）∑mk=1Wjkek，j=1，2，…，lbk=bk+ek，k=1，2，…，m（6）

2 基于BP神经网络的太阳能收集预测

2.1 数据来源

本文数据来源于National Renewable Energy Laboratory（美国国家可再生能源实验室，NREL）收集的太阳能数据[15]，数据真实可靠。由于收集的太阳能量受环境影响较大，且每种影响参数（温度、湿度、天气情况等）的影响程度不一。因此，忽略详细环境因素，只获取每天全球收集太阳能量的平均值（单位为W/m2）。数据中包含收集太阳能的日期、每天的时间段以及收集的太阳能量。通过对数据进行预处理发现，太阳能的采集量受季节影响较大，为了能够使得数据更加简单精准，在实际训练和预测过程中，选择将每年4月份每天第12个小时内（即1小时精度）收集的太阳能量作为输入数据值。本文选用每天时间间隔为12的收集太阳能量平均数值作为实际的训练和预测数据。

2.2 算法预测性能指标

在数据预测问题研究中，需要统一选取一些参数作为算法优劣的评价指标，从而使得评价更具公平性。本文拟采用的常用数据误差分析指标如下：

（1）绝对误差（AE，Absolute Error）：是指预测值与期望值之间的差的绝对值，如式（7）所示。

AE=|Tpred-Treal|（7）

（2）相对误差（RE，Relative Error）：是指预测值与期望值的差的绝对值与期望值的比值，如式（8）所示。

RE=|Tpred-Treal|Treal（8）

（3）平均绝对百分比误差（MAPE，Mean Absolute Percentage Error）：是指相对误差的绝对值的平均数，如式（9）所示。

MAPE=∑|Tpred-Treal|TrealN（9）

（4）均方根误差（RMSE，Root Mean Square Error）：是指均方误差的开方，也称作为标准误差，如式（10）所示。

RMSE=ε21+ε22+…ε2nN（10）

（5）均方根相对误差（RMSRE，Root Mean Square Relative Error）：是指所有数量样本的相对误差的平方比上样本数量的开方，如式（11）所示。

RMSRE=Σ（Tpred-TrealTreal）2N（11）

（6）RR（R2，拟合程度，也称为拟合优度判定系数）：表示数据的拟合程度，体现了回归模型中自变量变异在因变量变异中所占的比例，可用来衡量预测的数值与真实值之间的相关关系，体现的是预测算法的预测拟合程度。预测算法的RR值越靠近1，说明算法的预测效果越好。

对上述列举的数据预测常用指标进行分析可知，绝对误差AE、相对误差RE容易受到某个数据影响出现极端现象，因此用于显示某个算法下各数据的预测情况。平均绝对百分比误差MAPE、均方根误差RMSE和均方根相对误差RMSRE这3种误差都是预测算法下多个预测结果的平均误差，因此可以用于多个预测算法的性能对比，避免因为某一组数据异常而较大影响算法的预测结果。特别是平均绝对百分比误差MAPE，通过其值能够很直观地看出模型对于整体数据样本的相对误差的数量，是对整体数据误差求平均值；RR能够表示算法模型的拟合程度，是预测领域常常被应用到的一个评价指标，对于算法预测结果的评价也有着非常重要的意义。endprint

2.3 BP神經网络模型参数选择

本文利用BP神经网络进行太阳能预测的算法包括3个步骤：BP神经网络构建、BP神经网络训练以及BP神经网络预测。算法流程如图2所示。

在本文中，在利用神经网络进行太阳能收集功率预测具体操作时，将BP神经网络的构建输入层设置为1个，输出层设置为1个，隐藏层的设置按照式（13）确定。

l=n+m+α=1.414+αl=log2n=1l=nm=1（13）

式（13）中，l为隐含层节点数，n为输入层节点数，m为输出层节点数，α为1～10之间的常数。由上述隐含层l的取值可知，隐含层l的取值为1～1+α之间的数。以隐藏层数为l为例，将数据传入BP神经网络算法中运行得出相关结果。需要注意的是，在利用神经网络进行计算时，由于算法中网络权值和阈值是随机生成的，因而可能出现一组数据结果较好或较差的情况，因此需要多次模拟取平均值以避免陷入局部最优而带来结果的不准确性。

表1显示的是隐藏层数为1层时，在训练数据集上每次运行BP神经网络算法时所获取的各项评价指标值。同样地，将隐含层层数取值为1～10，得出不同隐藏层数下各项评价指标的平均值，如表2所示。表2显示，当隐含层数为4时，各项评价指标相对较小，此时预测模型最优。因此，本文将神经网络的隐藏层数设置为4来构建BP神经网络预测模型。

3 预测结果对比与分析

基于NERL太阳能收集真实数据集[15]，对本文提出的基于BP神经网络的太阳能收集功率预测方法进行深入分析，并将其与现有其它典型的数据预测算法进行预测结果对比，综合评价本文中采用的基于BP神经网络的太阳能收集功率预测算法。本文的实验仿真在MATLAB平台下实现。

3.1 BP神经网络不同隐含层下预测性能对比

在测试数据选择上，选取2008-2017年每年4月份每天12点的数据共300条。前270条（2008-2016年每年4月份）数据作为训练数据，后30条（2017年4月份）数据作为待预测数据。图3和图4是分别在BP神经网络（BPNN）算法隐含层分别为1、4和9时BPNN预测算法的绝对误差和相对误差比较结果。从图3和图4中可以看出，在隐含层为4的情况下，BP神经网络的预测效果最好，这与2.3节中的分析是一致的。

3.2 BP神经网络与其它预测算法性能对比

在BP神经网络隐含层为4的前提下，将BP神经网络方法分别与其它一些典型数据预测算法进行对比。选取卡尔曼滤波算法（Kalman Filter）、自回归移动平均算法（AutoRegressive Integrated Moving Alogrithm，ARIMA）与K最邻近算法（K Nearest Neighbor，KNN），在相同数据集下，与BP神经网络预测算法进行深入对比分析。

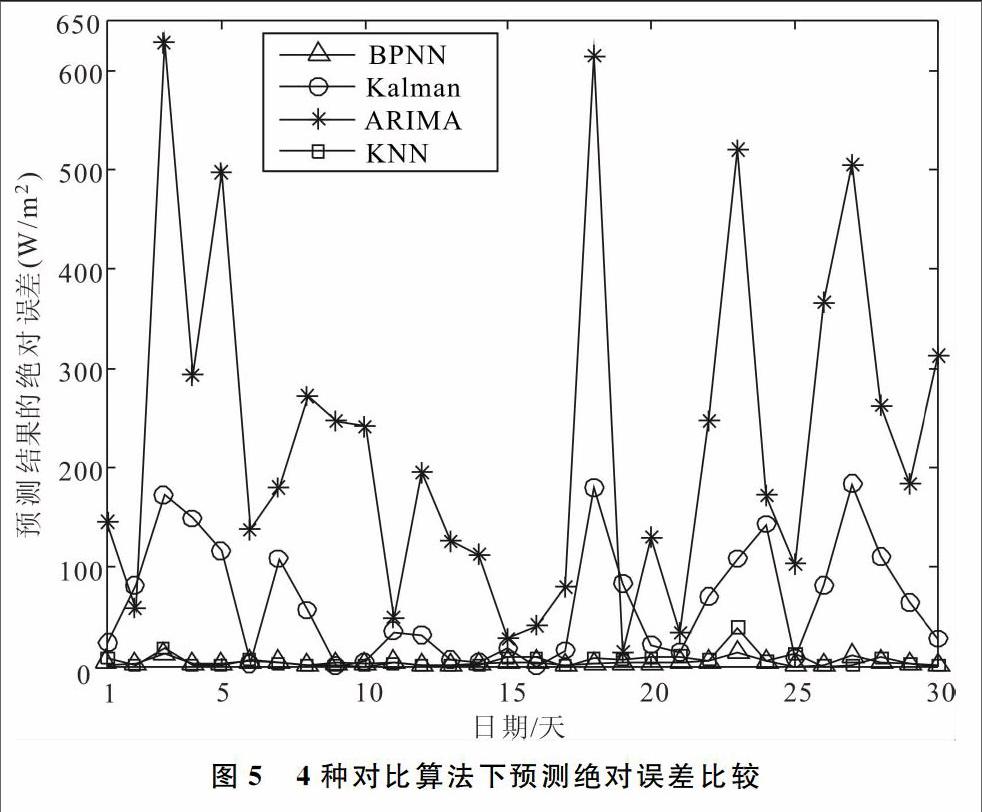
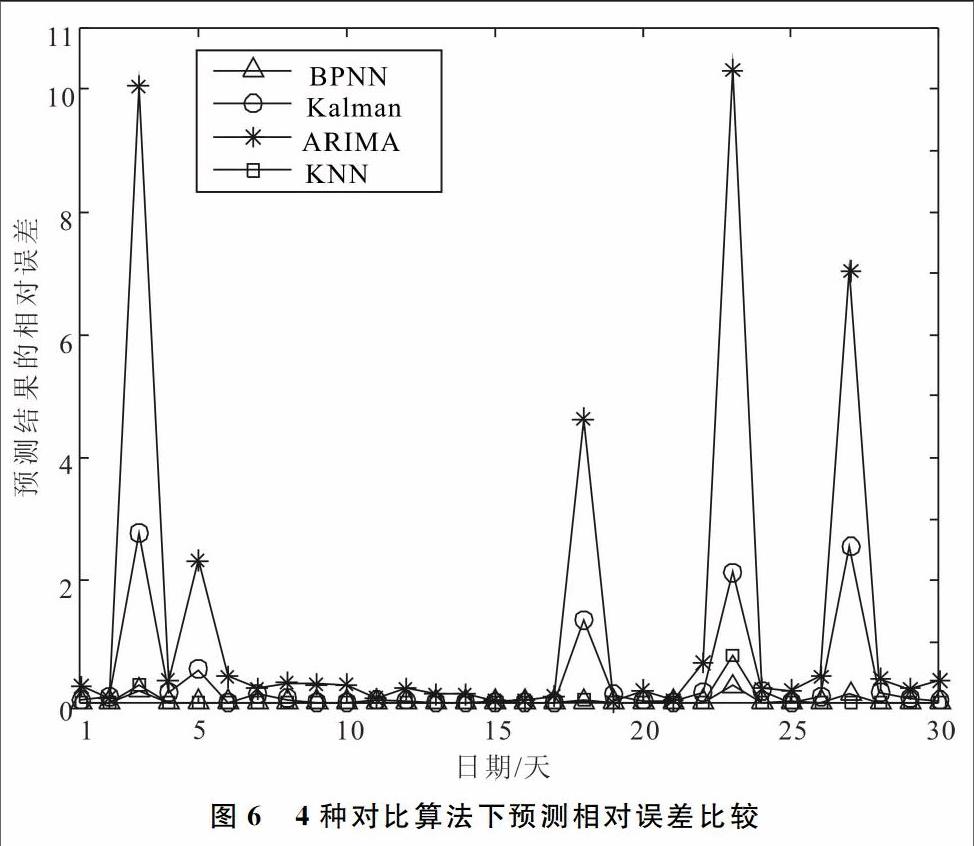
图5和图6是BP神经网络算法（BPNN）、卡尔曼滤波算法（Kalman）、自回归移动平均算法（ARIMA）和K最邻近算法（KNN）在预测数据的绝对误差和相对误差上的对比。可以看出，本文采用的BP神经网络算法预测效果最好，KNN算法的预测效果接近BP神经网络，但是仍不如BP神经网络方法。4种算法中，ARIMA算法的预测效果最差，这是因为ARIMA是时间序列预测模型，而太阳能能量收集易受天气、温度等其它因素影响，处于易波动状态，因此ARIMA预测效果不佳，而BP神经网络方法使用数据训练时的非线性变换和映射克服了这些不足，因此效果较好。

图7是4个算法在平均绝对误差（MAPE）、均方根相对误差（RMSRE）和拟合程度（RR）上的对比。从图7可以看出，本文采用的BP神经网络算法的误差仍旧是最低的（RR值越趋近1表示预测性能越好）。这些对比实验充分说明了本文采用的BP神经网络方法在太阳能收集功率预测问题上的有效性。

4 结语

在太阳能能量收集和利用系统中，基于能量预测可以进行系统任务的统一调度分配，提高系统工作效率和稳定性，因此能量预测研究具有重要意义。本文采用BP神经网络方法在真实数据集上对太阳能收集功率预测问题进行了研究，并与一些典型的数据预测算法进行了对比，仿真结果表明了本文BP神经网络算法的有效性。在后续研究中，有必要对在能量预测基础上的系统任务调度问题进行研究，探索能量预测在提高系统工作效率等方面的作用。

Li LingSheng1，Han Chong

（1.College of Computer Engineering，Jinling Institute of Technology，Jiangsu Nanjing 211169；2.College of Computer，Nanjing University of Posts and Telecommunications，Jiangsu Nanjing 210003）

参考文献：

[1] 江华.国内外光伏产业发展现状与趋势[J].太阳能，2016（12）：15-17.

[2] 丁明，王伟胜，王秀丽，等.大规模光伏发电对电力系统影响综述[J].中国电机工程学报，2014，34（1）：2-14.

[3] BHATTI N A，ALIZAI M H，SYED A A，et al.Energy harvesting and wireless transfer in sensor network applications：concepts and experiences[J].Acm Transactions on Sensor Networks，2016，12（3）：24.

[4] LIU Q，ZHANG Q J.Accuracy improvement of energy prediction for solar-energy-powered embedded systems[J].IEEE Transactions on Very Large Scale Integration Systems，2016，24（6）：2062-2074.endprint

[5] AKYILDIZ I F，VURAN M C.Wireless sensor networks[M].New York，NY，USA：Wiley，2010.

[6] 刘云浩.物联网导论[M].北京：科学出版社，2010.

[7] 钱志鸿，王义君.面向物联网的无线传感器网络综述[J].电子与信息学报，2013，35（1）：215-227.

[8] 徐向南.具有能量补给的异构传感器网络分簇路由算法研究[D].杭州：杭州电子科技大学，2015.

[9] BIASON A，ZORZI M.Joint transmission and energy transfer policies for energy harvesting devices with finite batteries[C].IEEE Journal on Selected Areas In Communications，2015，33（12）：2626-2640.

[10] SHU Y，SHIN K G，CHEN J，et al.Joint energy replenishment and operation scheduling in wireless rechargeable sensor networks[J].IEEE Transactions on Industrial Informatics，2017，13（1）：125-134.

[11] MOSER C，THIELE L，BRUNELLI D，et al.Adaptive power management for environmentally powered systems[J].IEEE Transactions on Computers，2010，59（4）：478-491.

[12] LIU Q，MAK T，ZHANG T，et al.Power-adaptive computing system design for solar-energy-powered embedded systems[J].IEEE Transactions on Very Large Scale Integration Systems，2015，23（8）：1402-1414.

[13] KANSAL A，HSU J，ZAHEDI S，et al.Power management in energy harvesting sensor networks[J].ACM Transactions on Embedded Computing System，2007，6（4）：32.

[14] PIORNO J R，BERGONZINI C，ATIENZA D，et al.Prediction and management in energy harvested wireless sensor nodes[C].In Proceeding of 1st International Conference on Wireless Communication，Vehicular Technology，Information Theory and Aerospace & Electronic Systems Technology，Aalborg，Denmark，2009：6-10.

[15] National renewable energy laboratory （NREL），oak ridge national laboratory.Irradiance and meteorological data[EB/OL].http：//midcdmz.nrel.gov/ornl_rsr/，2014.

[16] 周志華，陈世福.神经网络集成[J].计算机学报，2002，25（1）：1-8.

[17] 樊振宇.BP神经网络模型与学习算法[J].软件导刊，2011，10 （7）：66-68.endprint