基于串级PID技术与滑模控制的PMSM速度控制系统
2017-09-09张宇慧丁德锐王建华董晓光
张宇慧+丁德锐+王建华+董晓光
摘 要:永磁同步电机(PMSM)是一个非线性、强耦合系统,如何兼顾PMSM速度控制系统的快速性和稳定性一直备受关注。提出了一种新型的速度控制策略,可称为串级PID技术与滑模切换的混合控制策略,提高了PMSM系统的运行品质。具体地,利用新型串级PID技术取代传统PI调节器,提高系统的响应速度。在此基础上,设计了基于Sigmoid函数的指数趋近率的滑模控制器,在改善滑模趋近速度的同时抑制了滑模变结构的抖振问题。最后,借助于MATLAB仿真,验证了该控制方案,并与传统PI速度控制系统、普通滑模速度控制进行比较。结果表明該方案很好地兼顾了PMSM速度控制系统的快速性和稳定性。
关键词:串级PID;永磁同步电机;滑模控制系统;指数趋近率
DOIDOI:10.11907/rjdk.171340
中图分类号:TP319
文献标识码:A 文章编号文章编号:1672-7800(2017)008-0086-05
0 引言
近年来,永磁同步电机(PMSM),因其结构简单、体积小、运行效率高、功率大、无机械传感器控制系统等优点,逐步发展为市场的主流,广泛应用于城轨车辆、冰箱、空调、机器人等。由于PID控制系统具有算法简单、调节方便和可靠性高的优点,在永磁同步电机的调速控制系统得到广泛使用,但是由于PMSM是一个多变量、强耦合、非线性的复杂控制系统,使用常规PID的控制方法并不能满足高性能的控制要求。
为了提高系统性能,各种各样的高级算法被应用到PMSM控制系统中,其中包括神经网络控制、模型参考自适应控制、模糊控制、滑模控制[1-4]。由文献[5-6]可知,神经网络在电机应用中取得了良好的效果,但是神经网络的训练需要大量的样本,并且对样本的选取有较高的要求。而滑模控制系统的研究主要集中于快速性和稳定性,如文献[7]的速度控制系统采用指数趋近率,在一定程度上提高了PMSM的动态品质,但是系统的抖动仍然很严重。文献[8]设计了电流环与速度环的一体化滑模控制器,结果表明系统的稳定性和快速性明显增强,但由于参数的设定需要考虑众多因素,因此不易实现。文献[9]采用高阶终端滑模控制方法,提高了系统的鲁棒性和快速性,同时也消除了抖振,但是这种控制方法使系统实现变得复杂。
本文基于文献[10]提出的切换控制思想,并结合文献[11-13]的方法,设计了一种基于串级PID与Sigmoid函数指数趋近率的滑模速度控制系统。在系统启动和加速过程中采用串级PID控制系统,主要用于提高系统的快速性。当系统趋近滑动模态时切换到滑模运动状态,这样可以缩短滑模运动趋近模态的时间。具体地,本文在常规滑模面中加入了积分项,有利于消除系统的稳态误差[14];在指数趋近率的滑模控制系统中引入Sigmoid函数,有利于抑制负载引起的抖振,增强系统抗扰动能力。
下文对于串级PID技术与滑模控制的PMSM速度控制系统进行设计,并通过系统仿真及实验,验证所设计的系统在快速性、稳定性、抗斗振等方面的优势。
1 滑模控制原理
滑模控制是变结构控制系统的一种控制策略。这种控制策略与常规的控制的根本区别在于控制的不连续性,即一种系统结构随时间变化的开关特性。这种特性可以使系统在一定条件下沿规定状态轨迹作小幅度、高频率的上下运动,这就是所谓的“滑动模态”。这种滑动模态是可以设计的,并且与系统的参数和扰动无关[15]。因此,处于滑动模态的系统具有很好的鲁棒性。
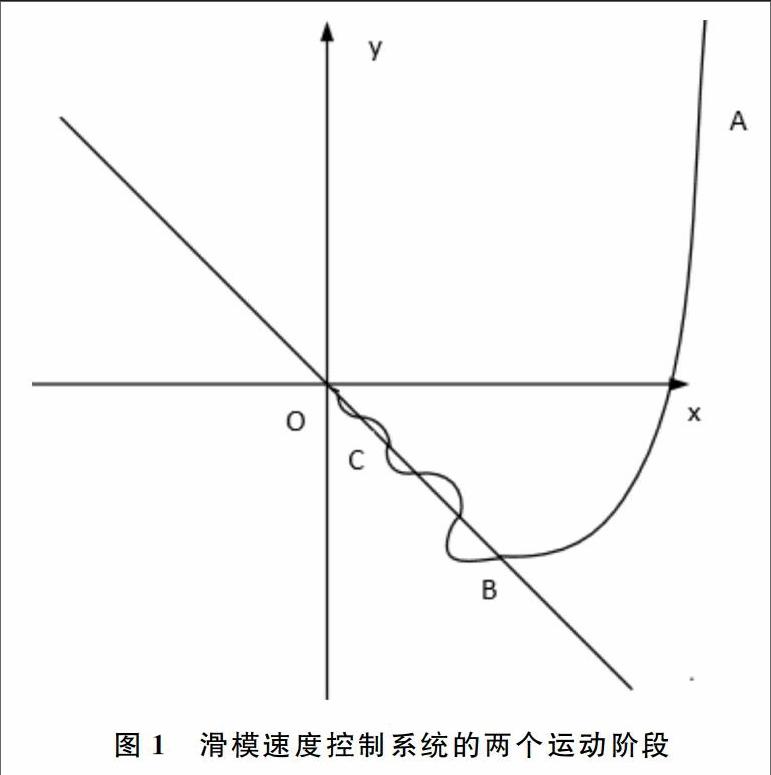
滑模变结构控制系统运动由两部分组成(见图1):第一部分AB是位于滑模面外的正常运动,它是趋近滑模面直到达到趋近运动阶段;第二部分BC是在滑模面附近并沿着滑模面s(x,t)=0的运动。
按照滑模控制理论的基本原理,正常运动阶段必须满足滑动模态的可达性条件ss′<0,才能实现系统的状态空间变量由任意未知的初始状态在有限时间内达到滑模面。因此,可以设计各种趋近率函数来保证正常运动阶段的品质。
2 永磁同步电机速度控制系统
2.1 基于Sigmoid函数的指数趋近率的设计技术
到目前为止,在几乎所有关于电机控制的文献中,滑模控制器均是通过符号函数或Sigmoid函数实现的。这两类函数的采用使得切换操作简单并易于实施。然而,在响应速度、抖振与超调量方面还存在很大改进空间。为此,本文采用指数趋近率滑模变结构控制器,结合已有研究成果,给出这一新颖的切换规则。
众所周知,Sigmoid函数为:
F(x)=21+e-ax-1,a>0(1)
其中a为正常数,用于调节Sigmoid函数的斜率。当a无穷大时,Sigmoid函数可转化为符号函数。Sigmoid函数具有一定的抗抖振性,但是它的响应速度较慢。为了在保证抗抖振性的同时提高响应速度,本文采用如下切换函数:
=-εF(s)-qs,q>0,s>0(2)
其中s代表滑模面,q和ε是两个待设计的参数。式(2)被称为基于Sigmoid函数的指数趋近率。
值得进一步指出的是,上述指数趋近率由两项组成:其中-qs是指数趋近项,q展现了指数级趋近速度,q越大速度越快,趋于滑模面的耗时越短;-εF项主要用来消除抖振[16]。此外,如果增加常数ε,正常运动阶段收敛速度加快,但滑动模态阶段的抖振将加强;如果减少常数ε,滑动模态阶段的抖振减弱[17],但正常运动阶段收敛速度变慢。明显地,减少抖振与增强收敛速度存在矛盾,在电机启动阶段或变速阶段,这一矛盾特别突出。因此,如何有效地权衡这两个性能指标,是一个非常重要的问题,在下文中将提出一种切实可行的解决方案。
2.2 基于Sigmoid函数的指数趋近率滑模速度控制
2.2.1 永磁同步电机数学模型endprint
假设PMSM的输入电流为三相对称正弦电流,忽略电机铁心饱和,不计铁心涡流,转子上无阻尼,转子与定子共同作用的磁场为正弦波,根据表贴式PMSM的电机特性[11],d-q坐标下的定子电压与转矩方程为[18]:
ud=Rsid+Lsdiddt-pnwLqiquq=Rsiq+Lsdiqdt+pnwLdid+pnwψfJdwdt+Bw+TL=TeTe=32pnψfiq(3)
其中:ud、uq分别为定子电压在d、q轴上的分量,id、iq分别为定子电流在d、q轴上的分量,Rs和Ls为定子的电阻和电感,w为角速度,TL和Te分别为负载和电磁转矩,J为转动惯量,B为摩擦系数,Pn为转子极对数。当采用id=0的转子磁场定向控制方法时,式(3)可以推导出PMSM的状态方程为[17]:
diqdt=1Ls(-Riq-pnψfw+uq)dwdt=1J(-TL+3pnψf2iq)(4)
2.2.2 滑模控制器设计
定义PMSM系统的状态变量:
x1=-wx2=1=-w′(5)
式(5)中为给定转速,w为实际转速。由式(4)和式(5)得系统状态空间方程:
x′1=-w′1=1J(TL-3pnψf2iq)x′2=-w″2=3pnψf2Ji′q(6)
令a=3pnψf2J,u=i′q,则式(3)-式(6)可简化为:
x′1x′2=0100x1x2+0-au(7)
定义滑模函数为:
s=cx1+x2(8)
其中c>0为待定参数。
常用的趋近率函数有等速趋近、指数趋近、幂次趋近等,但是它们都不能同时具备缩短到达滑模面的时间和消除抖动。为此,基于Sigmiod函数并结合式(2)、式(7)和式(8),本文提出如下指数趋近率的控制器:
u=(cx2+εF(s)+qs)/D(9)
进而根据积分公式,可得输出电流iq为:
iq=∫t01Dcx2+εF(s)+qsdτ(10)
从式 (10)可以看出,系统的被控输出中含有积分项和Sigmoid函数,积分项可以有效地消除稳态误差,Sigmoid函数可以抑制滑模面上的抖振现象,从而有利于提高系统的动态品质。
2.3 串级PID速度控制系统
在三相永磁交流调速矢量控制系统中,速度控制器普遍采用传统的PI调节器,其具有算法简单、可靠性高及参数整定方便等特点。然而PMSM是一个非线性、强耦合的多变量控制系统,当控制系统受到外界扰动的影响或者电机内部参数发生变化时,传统PI控制算法并不能满足实际要求。
此外,单级PID控制不能满足其控制精度。因此,本文提出串级PID控制方案,如图2所示。
在图2中,内环的PD控制为加速度控制回路,外环PI控制为速度控制回路。值得一提的是,在PD控制环,有别于现有的控制方案,在PSMS系统中引入角加速度的反馈信号,调节外环回路的输出大小,进一步改进系统的控制品质。由于采用速度回路和加速度回路的双闭环系统,串级PID控制系统提高了速度控制系统的启动和加速过程的快速性。然而由于PID控制的固有缺点,不可能同时提高快速性和降低超调量。
2.4 串级PID控制器与滑模速度控制器之间切换
上文详细叙述了本文的两大主要创新模块。接下来,笔者将依据电机速度的变化,构造串级PID控制器与滑模速度控制器的切换方案。这将使其同时拥有串级PID技术与具有指数趋近率的滑模控制的优点,即在消除抖振的同时提高趋于滑模面的转速。具体地,在电机启动、加速和受到较大扰动时采用串级PID,当转速达到设定值的95%后采用滑模控制技术。
图3为串级PID与滑模控制器切换框图,其中wr为电机的速度设定值,w为电机的实际速度。w经控制器来控制切换开关,当|wr-w|小于速度设定值wr的95%时,PMSM速度控制系统采用串级PID控制;当|wr-w|大于速度设定值wr的95%时,PMSM速度控制系统采用滑模控制。
3 PMSM系统仿真与实验
3.1 串级PID及仿真结果分析
为了验证串级PID的效果,在给定转速为1 000r/min时,分别进行串级PID和传统PID的PMSM速度控制系统仿真。图4和图5分别给出了串级PID系统模型及其仿真结果。
在图5中,图5(a)代表串级PID控制作用下的PMSM的转速图,从中不难发现在运行 0.015s后,PMSM的转速基本稳定在1 000r/min;图5(b)代表传统PID控制作用下的转速图。从仿真结果来看,系统在运行0.022s后才能基本稳定在1 000s/min。通过对比,不难发现串级PID控制系统不仅具有较小的超调量,还拥有较快的响应速度。
3.2 基于Sigmoid函数的指数趋近率的滑模速度控制模型搭建
3.2.1 基于Sigmoid函数的指数趋近率模型搭建
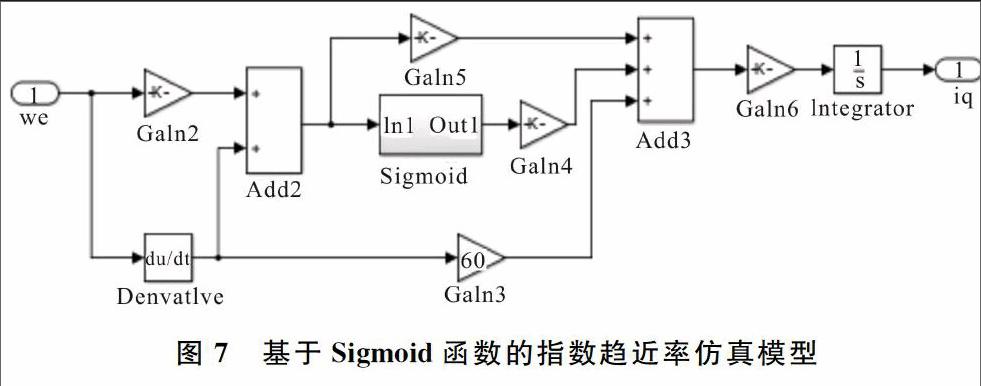
由式(1)、式(10)分别可搭建基于Sigmoid函数仿真模型、指数趋近率仿真模型,如图6、图7所示。
3.2.2 切换模型搭建
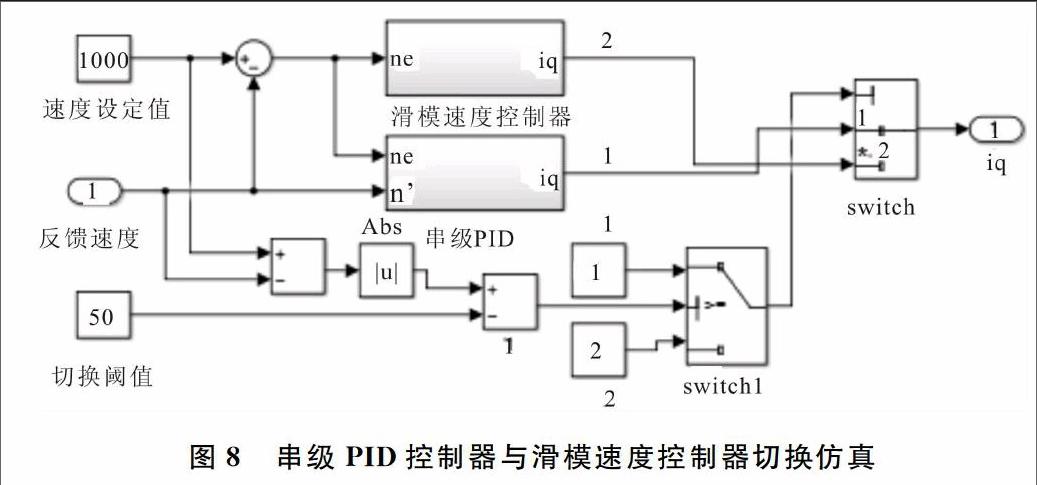
为了协调PMSM速度控制系統的快速性和稳定性,本文提出如图8所示的基于指数趋近率的滑模速度控制器与串级PID控制器的切换控制策略。当速度设定值与反馈值误差的绝对值大于切换阈值时,switch1输出第1路信号,此时串级PID起作用;当误差绝对值小于切换阈值时,Switch1输出为第2路信号,此时指数趋近率的滑模速度控制器起作用。
3.3 串级PID控制器与滑模速度控制器的切换控制策略及仿真结果分析
3.3.1 仿真系统平台搭建endprint
根据上一章节介绍的相关理论,笔者在Simulink中搭建PMSM的调速模型(见图9),主要包括串级PID控制算法、基于Sigmoid函数指数趋近率的滑模速度控制算法、开关切换模块、CLARKE变换及其逆变换、PARK变换及其逆变换、SVPWM 计算、逆变器、电机本体及检测等部分,采用 Sim Power Systems 库中的永磁同步电机模型作为被控制对象,控制系统整体仿真模型如图4所示。PMSM主要仿真参数为:极对数pn=4,定子电感Ls=8.5mH,定子电阻Rs=2.875Ω,磁链ψf=0.175Wb,转动惯J=0.003kg·m2,PWM开关频率设置为fpwm=10kHz,采用变步长Ode32tb算法,相对误差设置为0.0001,仿真时间设置成0.2s。
3.3.2 仿真结果与分析
根据如图9所示的仿真系统,检验所提出的控制策略在快速性以及抗扰动性方面的改进。在仿真中,负载给定值都在0.1s时由1N·m突变为15N·m,速度设定值均为1 000r/min,仿真时间为 0.2s。图10给出了传统符号函数的滑模速度控制系统速度响应曲线。对应地,本文的结果展现在图11中。通过对比不难发现:①当速度上升到950r/min后,速度控制系统由串级PID切换到Sigmoid函数指数趋近率的滑模速度控制系统;②当0.1s系统受到扰动过大时速度控制系统由串级PID与Sigmoid函数指
数趋近率的滑模速度控制系统之间进行相互切换。整个切换过程没有明显的抖动,系统响应良好。
更细致地对比可以看出:①在0.1s时当负载发生突变时本文新型速度控制系统很快趋近滑模面,远远优于符号函数的滑模速度控制系统;②经过串级PID切换的改进滑模控制器在0.01s时趋近滑模面,不经过串级PID切换的普通滑模控制器在0.03s时趋近滑模面,由此可得经过串级PID切换的滑模控制远远优于不经过串级PID切换的滑模控制。因此,基于串级PID与Sigmoid函数的指数趋近率滑模控制器性能最优。
为了进一步验证Sigmoid函数在指数趋近率的滑模控制系统中具有消除抖振的作用,本文分别给出了Sigmoid与符号函数的指数趋近率的速度波形图,它们分别对应图12(a)和图12(b)。图12为转速的设定值与转速的实际值相减得到,对比可知经过Sigmoid函数的PMSM的输出速度抖振现象可以被消除。
4 结论
本文设计的PMSM速度控制系统适于在实际生活中应用。该系统基于串级PID技术与指数趋近率的滑模控制技术,继承了串级PID技术的快速响应、滑模控制技术的抗干扰能力、指数趋近率的滑模速度控制对干扰的快速响应[19],以及Sigmoid函数在滑模中使用的抗抖动性,从而提高了PMSM速度控制系统的快速性和稳定性。仿真结果表明串级PID与基于Sigmoid函数指数趋近率的滑模速度控制有效提高了PMSM转速系统性能,为提高PMSM调速系统的动态品质提供了一种有效的方法。
参考文献:
[1] LI H R,WANG X Z,GU S S.An improved recursive prediction error algorithm for t raining recurrent neural networks[C].Proceedings of the 3rd WC ICA,2000:1043-1046.
[2] YAN JIANHU,LIN HEYUN,FENG YI,et al.Improved sliding mode model reference adaptive system speed observer for fuzzy control of direct-drive permanent magnet synchronous generator wind power generation system[J].IET Renewable Power Generation,2013,7(1):28-35.
[3] BOSSANYI E A.GH bladed theory manual[R].UK-Bristal:Grand Hassan and Partner Limited.2009:13-36.
[4] LAI C K,SHYU K K.A novel motor drive design for incremental motion system via sliding mode control method[J].IEEE Transactions on Industrial Electronics,2005,52(2):499-507.
[5] 戴先中,張兴华,刘国海,等.感应电机的神经网络逆系统线性化解耦控制[J].中国电机工程学报,2004,24(1):112-117.
[6] 孙玉坤,任元,黄永红.磁悬浮开关磁阻电机悬浮力与旋转力的神经网络逆解耦控制[J].中国电机工程学报,2008,28(9):81-85.
[7] 袁雷,胡冰新,魏克银.现代永磁同步电机控制原理及MATLAB仿真[M].北京:北京航空航天大学出版社,2016.
[8] CHEOL I B,KIM K H.Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J].IEEE Transactions on Control Systems Technology,2000,8(1):47-54.
[9] 郑剑飞,冯勇,陆启良.永磁同步电机的高阶终端滑模控制方法[J].控制理论与应用,2009,26 (6):297-700.endprint
[10] 徐文伟.永磁同步电机矢量控制的实现[D].广州:华南理工大学,2013.
[11] 冯庆瑞,裴海龙.串级PID在无人姿态控制的应用[J].控制系统,2009,22(1):43-45.
[12] FENG Q D,FEI H L.The application of cascade PID control in UAV attitude control[J].Control system,2009,22(1):43-45.
[13] 張晓光,孙力,赵克.基于负载转矩滑模观测的永磁同步电机滑模控制[J].中国电机工程学报,2012,32(3):111-116.
[14] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,25(1):431-432.
[15] 李永刚,李星野,史先鹏.基于扩张状态观测器的一类未知非线性不确定系统滑模控制[J].上海理工大学学报,2010,32(2):111-114.
[16] MICHAILZ.Terminal attractors for addressable memory in neural network[J].Physics Letter A,1988,33(1-2):18-22.
[17] 侯利民,张化光,刘秀种,等.PMSM无速度传感器最优转矩控制系统的研究[J].仪器仪表学报,2009,30(4):706-710.
[18] LIN F J,SHEN P H.Robust fuzzy neural network sliding-mode control for two-axis motion control system[J].IEEE Transactions on Industrial Electronics,2006,53(3):1209-1225.
[19] XU J Y,LIU H P.Variable speed system of permanent magnet synchronous motor with optimal current control by the MR-ILQ design method[J].Proceedings of the CSEE,2007,27(15):21-27.endprint
