基于IFS码的分形图形生成算法研究

陶雪娇+陶薇薇

摘 要：迭代函数系统（Iritated Function System，IFS）是一种利用迭代或递归方式，将满足收敛性的数学对象进行反复计算并拼贴生成具有分形特征作品的方法。首先从二维IFS公式原理上研究了分形图形的拼贴公式以及推导；然后将分形作品按照自相似特征进行解析，形成多个仿射变换拼贴；再从整体到局部缩放、旋转、平移等变换的角度，分析仿射变换指数的变化规律，得出IFS码；最后对分形图形进行了仿真分析。

关键词：迭代函数系统；放射变换；分形图

DOIDOI：10.11907/rjdk.171460

中图分类号：TP312

文献标识码：A 文章编号文章编

号：1672-7800（2017）008-0053-03

0 引言

随着数学与计算机学科发展，依托公式递归与迭代方式生成数字分形作品的艺术形式发展很快，分形艺术作品也在平面、视频、影视、动画、压缩等领域得到了较好应用[1]。迭代函数系统（Ireration Function System，IFS）是基于函数迭代原理的仿射变换系统，是生成数字分形图形的重要方法之一，在分形图形数字生长中最具发展前景。IFS系统可以选取迭代函数，生成IFS吸引集，通过仿射变换（Affine Transformation）实现二维坐标之间的线性变换，保持二维图形的“平直性”[2]。

1 二维平面的仿射变换拼贴原理

任何分形图形都具有整体与局部相似的特性，每一组相似可视为从整体到局部的一个仿射变换，多个仿射变换集进行拼贴就能形成复杂的分形图像。二维平面的IFS公式[3]如下：

S=Un[]i=1Fi（S）Pi（1）

其中，S是二维平面的点集，仿射变换是一个二维点集到二维点集的映射，其中Fi即仿射变换的变换函数， N个仿射变换函数映射的并集拼贴形成一个具有自相似特性的分形图形，Pi是该变换函数在仿射拼贴中的权重值。

Fi是一个仿射变换的映射公式，Vj本身可以是任意的迭代算法，如线性（linear）、旋涡（swirl）、球形（spherical）等变换，可以写成如下形式：

Fi（x，y）=Vj（aix+biy+ei，cix+diy+fi）（2）

由式（2）可以看出，Fi输入了一个点（x，y），然后传入Vj进行线性变换，其简化形式可以用式（3）表达：x′=ax+by+ey′=cx+dy+f（3）

式（3）可转化为矩阵表达式：

x′y′=a cb dx[]y+ef=Txy+ef（4）

从式（3）和式（4）可以看出，Fi的仿射变换即是对（x，y）点进行缩放、旋转、拉伸、平移等线性操作，（x，y）是仿射变换前的点坐标，（x′，y′）是仿射变换后的点坐标，a、b、c、d、e、f是仿射变换系数，当把式（3）变成式（4）时，系数是矩阵的形式，便于在Matlab中计算和实现。在绘制某个分形图形时，应当先分析分形图形的自相似性，确定仿射变换系数。

当绘制的分形图形比较复杂时，需要多个仿射变换，即确定仿射变换集{ωn}。多个仿射变换的结果会拼贴在一起进行迭代，此即IFS的拼贴原理。每个仿射变换在拼贴时所占比重不一样，也即仿射变换集会对应一个比重集P=[p1，p2，p3]。

2 仿射变换生成IFS码

以经典的sierpinski三角为例，如图1所示。垫片由3个基本的仿射变换组成，完整的垫片由这3个三角形进行各自仿射变换形成。由于这3个部分的形状完全一样，所占的比重也一样，都是1/3，所以，P=[1/3，1/3，1/3]。

根據图1可以分析出3个三角形相对于原始三角形的线性变换关系：原始三角形迭代后的形状边长是原边长的一半，因此式（4）中的T可以确定为：

T=0.5 00 0.5（5）

3个三角形的起始坐标可以确定为（0，0），（1，0），（0.5，3/2），这3个坐标是迭代后3个三角形的坐标偏移量。很明显在第二次迭代时，大三角形中间挖空了一个倒立的正三角形，可以将其解读为3个同样大小的三角形拼贴到一起，也即三角形①由原三角形边长缩放到1/2且不平移，三角形②由原三角形缩放到1/2且平移坐标（1，0），三角形③由原三角形缩放到1/2且平移坐标（0.5，sin（pi/3））。缩放对应到式（4）中x和y的系数，即a与d，而平移对应到式（4）的e和f。迭代出来的3个三角形大小一样，意即3个仿射变换的比重一样为1/3，因此得出垫片的IFS码。3个三角形的权重相等，因此概率因子pi用1等分，即pi=1/3，得到3个线性变换的IFS码，见表1。

每一次迭代都采用相同的系数获取映射点集、迭代数次，得到分形图。执行上述程序输出的图形如图1所示。从Matlab的输出结果可以看出，这是一个具有典型的自相似性的三角形垫片，初始是一个黑色的三角形，每次切掉中间倒立的正三角形，如此迭代，可得到sierpinski垫片。在IFS迭代函数系统中，迭代次数越多效果越清晰。

用同样的方式可得出koch曲线的IFS码，如图2所示。第1次迭代时，koch曲线是一条直线，而第2次迭代时，koch曲线变成了4段，每一段等长，可以看作4个仿射变换，每个仿射变换的权重相等，因此概率因子pi用1等分，即pi=1/4。很明显，在第二次迭代时，可以将其解读为4个同样大小的线段拼贴到一起，也即是线段①由原线段边长缩放到1/3且不平移，线段②由原线段缩放到1/3且逆向旋转60°且平移坐标（1/3，0），线段③由原线段缩放到1/3且正向旋转60°且平移坐标（0.5，1/sqrt（12））， 线段③由原线段缩放到1/3且平移坐标（2/3，0）。缩放对应式（4）中各自的x、y系数，旋转需要将坐标进行三角变换，而平移到式（4）的e和f，由此得出垫片的IFS码，见表2。endprint

只要分析清楚对象的自相似特性，就可以建模具体的仿射变换进行拼贴，再根据公式（4）分析出各自的仿射变换IFS码。

用同样的方式可以得出分形树的IFS码，如图3所示。第1次迭代时，分形树是一条直线，而第2次迭代时，分形树变成了5段，每一段等长，可以看做5个仿射变换，每个仿射变换权重相等，因此概率因子pi用1等分，即pi=1/5。很明显在第二次迭代时，可以将其解读为5个同样大小的线段拼贴到一起，也即是线段①由原线段边长缩放到1/3且不平移，线段②由原线段缩放到1/3且逆向旋转30°且平移坐标（0，1/3），线段③由原线段缩放到1/3且平移坐标（0，1/3）， 线段④由原线段缩放到1/3且正向旋转30°且平移坐标（0，2/3），线段⑤由原线段缩放到1/3且平移坐标（0，2/3）。缩放对应到式（4）中各自x和y的系数，旋转需要将坐标进行三角变换，而平移对应到式（4）的e和f，得出垫片的IFS码，见表3。

由以上例子可知，在进行缩放时，所有的系数abcd都需要乘以缩放系数。进行旋转时，逆时针旋转角度取正，顺时针旋转角度取负，坐标系数需要进行三角变换，即T系数变换：

T=cosθ -sinθsinθ cosθ（6）

3 IFS碼引入随机参数

在构造森林时，考虑到森林中树的随机性，可以将随机参数引入IFS码。但不同的树木分形特征差异较大，如枫叶与蕨类植物的叶子具有极大的差异性[4]，可以构造不同的仿射变换来生成分形树，如图4第一棵树与第二棵树是两个不同时令不同物种的分形树。

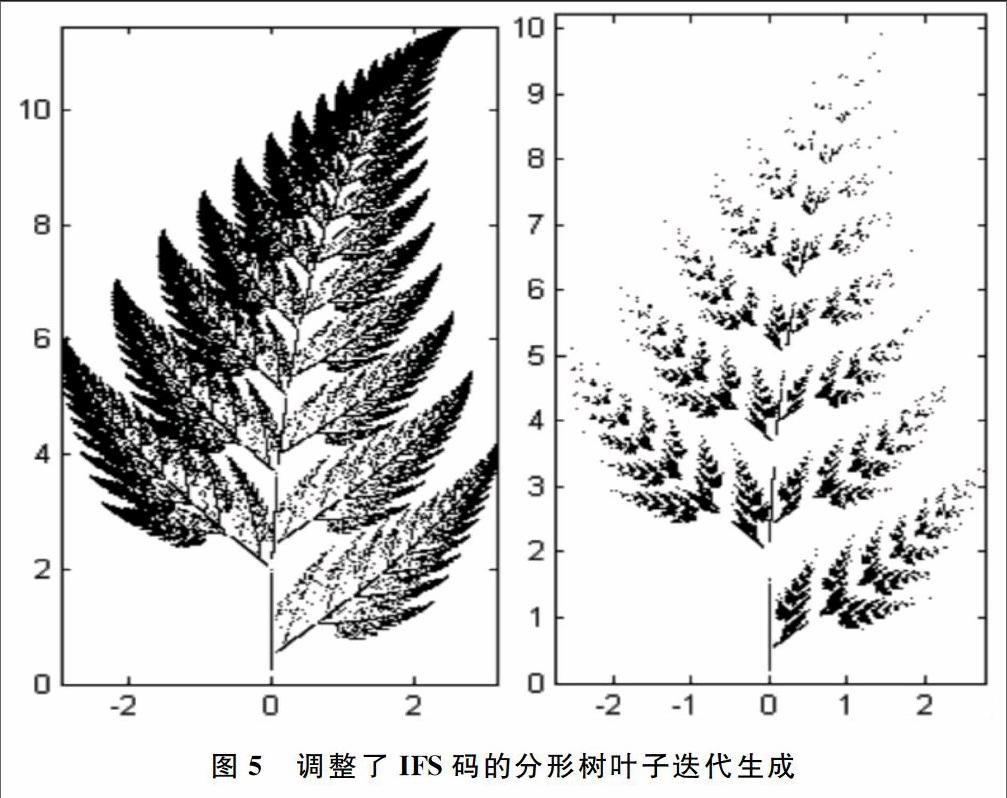
同一种对象的仿射变换特征相似，可以引入随机函数构造同一物种不同外观的树或树叶。图5是引入了随机参数到IFS后生成的同一物种不同外观的树叶。

4 结语

自然界有许多具有自相似特性的分形结构，如雪花、分形厥、树冠等，通过分析分形图整体与局部的仿射变换特性，计算出仿射变换的旋转、平移、缩放指数，构成IFS码，就可以对分形实物进行仿真[5]。但这种分析方式对大自然中具有不规则变换特性的分形图仿真效果较差，找到较为准确的IFS码需要多次尝试。下一步研究拟提出仿射变换建模算法，以提高IFS码生成效率与仿真准确率。

参考文献：

[1] 朱华，姬翠翠.分形理论及其应用[M].北京：科学出版社， 2011.

[2] 徐桂楠.数字艺术设计中的科学美 [J].科教文汇，2014（5）：132-133.

[3] 陶薇薇.基于数学分形生成数字艺术作品的方法研究[J].艺术品评，2017（1）：408-410.

[4] 朱海祥.基于 IFS 法的分形图形生成及优化设计[J].高师理科学刊，2016（36）：29-30.

[5] 刘志勇.基于分形技术与Matlab的树叶形态模拟仿真[J].重庆职业技术学院学报，2007 （16）：141-142.endprint