问题情境的创设：基于思维发展的理解

任 旭，夏小刚



问题情境的创设：基于思维发展的理解

任 旭，夏小刚

（贵州师范大学数学科学学院，贵州贵阳 550001）

问题情境是一类具有思考性和贴近学生现实的数学问题．创设问题情境，其主要任务就是把概念和定理中的数学关系由已知转化为需要思考和探索的未知关系，并置于与学生相关的现实背景中，其核心意义在于激发学生的问题意识，引发学生的数学思考．引导教师从衍生性主题的设计、数学内容本质的把握、数学关系的转化以及问题结构的明确等方面去创设问题情境，有助于彰显问题情境对学生思维发展的教学意义．

数学思维；问题情境；创设问题情境；数学教学

1 问题提出

众所周知，“双基数学教学”作为一种教学理念，已成为中国数学教育的重要组成部分．然而，在知识本位的课堂教学影响下，不少学生掌握知识，却不善于思考知识、追问知识．学而不思则罔，面对知识经济社会对实践和创新人才的不断需求，如何让学生通过数学学会思考，已成为数学教育实践中值得研究的一个重要话题[1~2]．无疑，对学生数学思维的培养，仅仅依靠知识和技能的传授是远远不够用的，必须改变那种重知识传授轻数学探究、重数学知识轻数学过程的观念．这意味着，数学教学必须回归本真，注重以问题驱动学生的数学思考．

基于此，数学课程标准（以下简称《标准》）提出教师要创设适当的问题情境，以引导学生通过实践探索，获得数学的知识技能、数学思考和解决问题的课程目标[3~4]．十多年来，问题情境创设已成为教师生活中的一种“日常行为”，问题情境被广泛运用于概念、原理、问题解决等不同类型的数学教学之中．然而，审视课堂，不难发现教学中问题情境创设的意义失落：一方面，问题情境拉近了数学与学生已有知识和经验的距离，激发了学生数学学习的兴趣和动机；另一方面，问题情境大多被局限在知识背景的认识范畴，并未成为学生构建知识、发展思维的“支架”．这表明教师对问题情境的认识大多还停留在价值和意义的经验层面，即通过创设问题情境来解决诸如兴趣、动机等方面的问题[5]．问题情境及其创设的本质是什么？如何构建一个问题情境创设的理论框架，以彰显思维发展的意义呢？对这些问题的进一步探讨，既是对问题情境创设的价值诉求，也利于学生数学思维的培养．

2 对问题情境创设的内涵分析

2.1 问题情境的本质

问题情境是一个含义多重的概念．研究者以“问题情境”、“数学”为主题，对近10年来CNKI中的相关文献进行梳理，发现由于研究者的潜在观念和理论价值倾向的不同，对问题情境的理解亦各有差异．下面是几种有代表性的观点：一是从激发学习兴趣的角度，把问题情境定义为“学生进行数学的活动时所处的学习环境”[6]、“教师根据教材中的某一个知识点进行提问，为提问而创设的一个课堂情境”[7]；二是从激发数学探究的角度，将问题情境定义为教师设立的“一系列有难度的问题”[8]、“通过设置一种具备一定困难，从而需要学生在付出一定的努力后，方可完成的教学任务”[9]、“组织学生‘再创造’式学习数学的依托”[10]；三是从引发认知冲突的角度，把问题情境视为“教学中个体觉察到的一种有目的但又不知如何达到这一目的的心理困境”[11]、学生“运用已经掌握的知识去研究新的未知问题的气氛”[12]；四是从问题解决的角度出发，将问题情境表述为“一种典型的能够引发产生问题并解决问题的情境”[13]．概括起来，关于问题情境的认识可以分为情境指向和问题指向两种视角，前者把问题情境的着力点放在学生的学习环境、课堂情境和心理困境上，后者则把问题情境看作是明确的数学问题或数学任务．这些认识突显了问题情境在如何有效促进学生认识和形成数学知识中的重要作用，但是缺少对两种指向的认识重心的整合．

问题情境的价值意义与时代的教育价值取向及其对教学实践的期待相联．在注重效率的工业化时代，基础知识和基本技能的传授成为教育价值的主流认识，教学意味着对知识和技能的“掌握”而不是“思考”．在信息时代背景下，数学成为生活与交流的工具，成为“思维的体操”，成为创造力的源泉．作为一种时代回应，数学教学开始由关注学生知识技能的发展转向更为关注数学核心素养的培养，即“帮助学生学会数学地看待世界，发现问题，表述问题，分析问题，解决问题”，其核心是学生“思维的发展”[14]．杜威曾经在《我们怎样思维·经验与教育》中指出：思维源于疑难的情境[15]，因此，当经验和疑难的情境对于学生思维发展具有重要影响[16]时，将问题情境的情境指向和问题指向两种视角进行整合，有利于拉近数学与学生生活世界的距离，更有助于促进学生在问题情境的观察与思考中去发现问题、分析问题和解决问题．

基于此，对问题情境作了如下定义，即问题情境是一类具有现实性和思考性的数学问题．其中，“现实性”是问题情境的外部特征，涉及学生生活世界中的客观现实、已有的数学知识经验以及其它相关学科的知识经验等；“思考性”则体现了问题情境的核心价值，表现在问题情境所蕴含的数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等活动中．

2.2 创设问题情境的内涵

问题情境的创设，主要指教师根据学生学习目标和学习内容的特定需要，把概念和定理中的数学关系由已知变化为需要思考和探索的未知关系，并置于学生相关的现实背景中；或者把已有的数学问题与学生相关的现实背景进行有机整合．由此为学生提供一类具有现实性和思考性的数学问题——问题情境．

问题情境的创设，其教学意义在于激发学生的问题意识，引发学生的数学思考．在问题情境的创设中，学生思维发展不仅被看作是一种教学目标，更被看作是一种应遵循的教学理念和精神．实现这种教学追求的关键，首先在于对学生已有知识经验的把握．为便于阐述，不妨将问题情境中的已知条件及学生已有的知识经验称为“已知区”，将问题情境所要解决的目标任务称为“未知区”．这意味着创设问题情境必须立足于学生的“最近发展区”，把握好“已知区”到“未知区”的距离，否则，难以激发学生的思维参与．

图1 创设问题情境的“三区”

其次，在于对不同类型问题情境难易度的理解和把握．为此，借助比格斯（John Biggs）教授提出的SOLO（Structure of the Observed Learning Outcome，观察到的学习结果的结构）评价理论[17]，把问题情境蕴含的数学问题分为单一结构、多元结构、关联结构和抽象拓展结构等4种水平，其结构特征具体如下：

单一结构水平（Unistructural Level）：解决问题只需一个数学知识或技能单元．

多元结构水平（Multistructural Level）：解决问题需多个数学知识或技能单元．

关联结构水平（Relational Leve1）：需调动多个数学知识或技能单元，并通过分析、归纳、综合才能解决．

抽象扩展结构水平（Extended Abstract Leve1）：需通过推理、演绎的方式，提出具有普遍意义的猜想或推论．

在此基础上，以情境的类别和问题难易度为维度，对创设的问题情境作如下划分（如表1），从而可以得到3（类别）×4种（思维水平）不同类型的问题情境．其中，P（，其中1≤≤3，1≤≤4）表示的问题情境，其思维层次随着的增加而增加．

进一步地，可以将其划分为两个方面的问题情境：

一是有思考价值和意义的问题情境——P（，其中1≤≤3，2≤≤4）表示的问题情境．

二是没有思考价值和意义的问题情境——P1（，且1≤≤3）表示的问题情境．

这种问题情境的类型划分，为彰显问题情境对学生思维发展的教学意义提供了一种认识基础．

表1 问题情境的类型划分

3 创设问题情境的基本框架

创设问题情境需要确立主题内容，明确“创设”的数学对象，即数学的概念、原理、思想和方法以及与学生现实相关的背景信息等．在此基础上，结合学生已有的知识经验，对“创设”对象蕴含的数学关系作必要的改进，并选用契合的问题结构和恰当的数学表征．因此，从创设问题情境的分析角度看，可以将问题情境的创设分为以下几个步骤．

3.1 设计衍生性主题

问题情境的创设，致力于通过学生对问题情境的观察和探索，使学生在获得知识与技能的同时，发展其在数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析等方面的思维能力．其中，知识技能的获得体现了数学学习内容的基础性价值，而数学思维的发展则反映了数学学习内容的衍生性价值．然而，哪些内容是需要学生基本了解，哪些内容需要学生通过思考去探究和发现，这是值得教师研究的教学问题．借用史宁中教授对数学核心素养的理解，即用数学的眼光观察数学世界，用数学的思维分析现实世界，用数学的语言表达数学世界[18]，可以为问题情境创设中的主题确立提供基本标准：（1）数学的价值；（2）课程内容核心；（3）具有探究性．显然，根据上述标准确定主题内容，并围绕这些主题内容创设问题情境，有利于学生感受数学的价值，主动探究知识，也有利于其思维能力的发展．比如高中数学中的集合、函数、数列、不等式、解三角形、统计、概率、平面向量与三角恒等变换等概念，由于它们居于数学课程的内容中心，蕴含了数学“再创造”的教学意义，体现了超越数学课堂的持久价值，因此容易成为衍生性主题内容的重要来源．

当然，衍生性主题内容的确立，必须考虑学生已有的知识经验，立足于学生的“最近发展区”，把握好“已知区”到“未知区”的距离．否则，容易导致教学内容探究性的丢失，进而遮蔽主题内容的衍生价值．以等差数列前项和为例．等差数列作为刻画一类离散现象的重要的数学模型，其前项和的公式及其推导蕴含了特殊到一般、类比和归纳等思想方法，因此成为高中数学教学中一个重要的衍生性主题内容．从教学实际情况看，教师大多习惯先介绍高斯利用“首末凑配法”求出1+2+…+100之和，然后运用学生在小学就已熟知的高斯算法，启发和引导学生去发现和运用求等差数列前项和的“倒序求和法”．无疑，这为学生提供了一个具有思维挑战性的问题情境，其中，联想和类比是解决问题所要运用的重要方法．显然，与“首末凑配法”、“倒序求和法”相比，这种基于类比的合情推理对学生数学思维的发展具有持久的价值和作用．不过，在实践中发现，由于“倒序求和法”与高斯算法的类比性不高，超越了学生已有的知识经验，以致学生在问题情境的思考和探索中，只能感慨高斯算法的“妙”，却难以由等差数列“首末凑配”联想到“倒序求和”．最终，等差数列前项和的公式及其推导内容的思维价值丢失．

3.2 把握教学内容的数学本质

创设问题情境，应明确教学内容的数学本质．对数学本质的认识，涉及数学的价值、数学的结构、数学的表现形式以及数学的文化等多种视角，因此其含义有多种，如数学是科学的工具、思维发展的手段，数学是模型，数学是符号，数学是理性和求真，等等．

把握教学内容的数学本质，重点首先在数学结构的分析，核心在思想方法的挖掘．以人教版等差数列前项和的教材分析为例：教材首先呈现高斯计算1+2+…+100之和的“首末凑配法”，以及利用“倒序求和法”求等差数列的前项和的问题，在此基础上，展现了用“倒序求和法”求等差数列前项和的推导过程．这种推导虽然容易使学生理解和掌握，但是没有体现“倒序求和法”的知识探究过程．为此，必须把握等差数列前项和的数学本质——一个关于、、的代数式，抓住渗透其求和过程中的数学转化思想和方法，通过的数学关系，将原有求和问题转化为一个简易级数的求和问题．

无疑，认识和把握好教学内容的数学本质，对于创设问题情境的意义至关重要．在此，应该摒弃把数学等同于演算科学的看法，关注数学作为一种人类文化创造的本质特征，从而以更为广阔的视角去透视数学，领悟数学的社会意义和文化意义，进而更好地理解和把握教学内容的数学本质[19]．这不仅有利于引导学生追求数学的真理美——抽象的概念、严格的推理、创新的方法、完美的形式以及精确的结论，而且可以更好地通过问题情境的创设，引导学生在数学自身的内在关系、相关学科知识以及现实社会文化背景的探究中，发展自己的想象、直觉、猜测、假设、检验、试错、归纳、试验等思维能力．

3.3 转化数学关系明确问题结构

数学关系即数学对象所具有的思维活动赖以依存的条件，是“数学对象间可以确切定义的关系”[20]，如对应关系、函数关系、同构关系、相等关系、不等关系、包含关系，等等．通常，教师可以采取一定的方法，如一般到特殊、抽象到具体、变换法（等价变换、不等价变换）、模型法等，将含有未知目标的数学关系(,)反映到一组较具体的数学关系（或具体的未知关系）和学生的相关现实背景中，以激发学生的数学思考．

从前面等差数列求和问题可以看出，由于“倒序求和法”与高斯算法的类比性不高，难以激发学生在求和问题情境中的思维参与，因此，教学的关键在于将等差数列前项和的本质关系转化为学生可以“触摸”和探索的数学问题，以此创设问题情境．譬如，可以采取一般到特殊、抽象到具体的方法，将等差数列前项和反映出来的S与1、a的数学关系进行特殊转化，即当=3，4，5，…时，

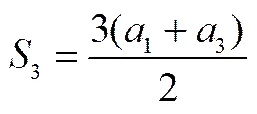
在此基础上，创设以下问题：

当=3时，如何用1，3表示3？

当=4时，如何用1，4表示4？

当=5时，如何用1，5表示5？

……

进一步地，让学生通过对下列等式的观察、归纳，思考如何用1，a表示S的问题．

……

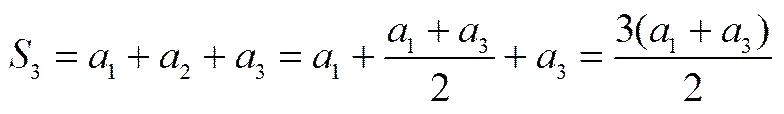
由于=3，4，5时，3与1和3的数学关系、4与1和4的数学关系以及5与1和5的数学关系，成为学生进一步探究S与1和a之间数学关系的信息背景，因此如何用1，a表示S的问题便构成了一个具有探究性的问题情境．

前面，根据SOLO评价理论，将问题情境分为单一结构、多元结构、关联结构和抽象拓展结构4种类型．问题结构类型的明确，为学生提供了观察、认识、分析和研究数学关系的切入点，也为教师进一步分析问题情境对学生的思维要求提供了条件．

然而，抽象的代数表征方式虽然具有简洁和可操作的特点，但是容易使问题情境过于抽象，因此在明确问题的结构类型后，为了降低学生的认知负荷，还应根据内容特点，采用文字表征、符号表征与视觉表征相结合的表征方式．比如，通过几何表征的方式，让学生思考等差数列前项和的几何意义（如图2）．

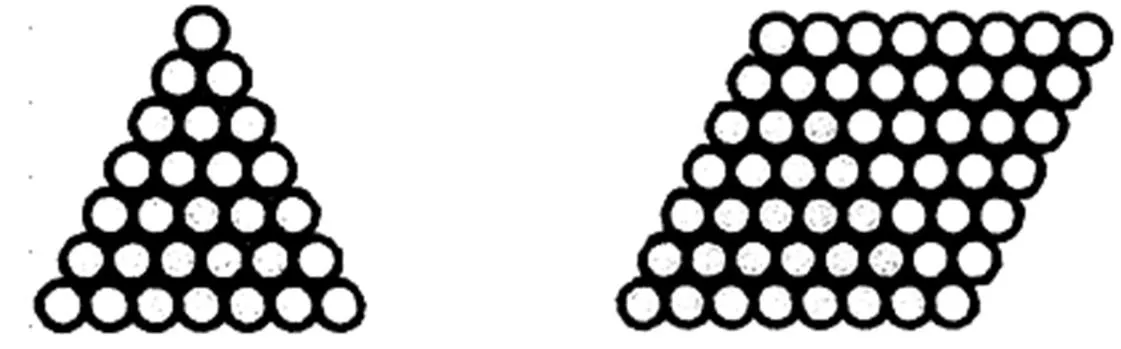
图2 梯形模型

4 结束语

在数学教学中，创设问题情境的一个重要任务就是促进学生在数学学习中的思维参与．问题是数学的心脏，思考是数学活动的主线，因此，问题情境广泛存在于基于数学概念、数学原理及问题解决的探究教学中．无疑，教师所创设问题情境“比书本上更加直接和富有感染力，并在更大程度上潜移默化地影响学生‘数学素养’的水平”[21]，然而，创设问题情境只是为学生构建知识、发展能力提供了条件．事实上，问题情境能否真正激发学生的思维参与，帮助学生获得数学知识技能、数学思想和数学活动经验，进而形成良好的数学思维品质和解决问题能力，这不只需要教师针对数学的基本概念、原理和重要的思想方法，从衍生性主题的设计、数学内容本质的把握、数学关系的转化以及问题结构的明确等方面去创设问题情境，还需要在此基础上对学生问题探究过程的引导，更需要教师形成对创设问题情境的反思及相关理论问题的思考．唯有如此，问题情境的创设才能调动学生的数学思考，彰显问题情境对学生思维发展的教学意义．

[1] 郑毓信．“数学与思维”之深思[J]．数学教育学报，2015，24（1）：1-5．

[2] 常磊．国内外高层次（数学）思维研究述评[J]．数学教育学报，2016，25（5）：9-16．

[3] 教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[4] 教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003．

[5] 杨玉东．教师运用数学问题情境教学的潜在观念与理论倾向[J]．上海教育科研，2014，（11）：54-56．

[6] 许玉梅．浅谈数学教学问题情境创设的重要性及原则[J]．教育教学论坛，2015，（4）：239-240．

[7] 高丽．问题情境在初中数学课堂中的践行探研[J]．中国校外教育，2013，（4）：98．

[8] 车成全．论教学中的问题情境及其创设[J]．教育探索，1999，（6）：46．

[9] 邱家寰．探析高中数学中如何设置问题情境启发学生[J]．教育教学论坛，2012，（24）：84-85．

[10] 李鹏．“中国”“美国”“巴西”数学教材“比和比例”内容的比较研究[J]．数学教育学报，2016，25（6）：46-50．

[11] 吴爱武，何永刚．数学课堂中优化问题情境创设的策略[J]．上海教育科研，2005，（6）：84-85．

[12] 王霞．数学教学中问题情境创造及提问艺术[J]．教学与管理，2006，（5）：72-73．

[13] 唐小丹．数学问题情境创设的有效性探讨[J]．教学与管理，2011，（9）：133-134．

[14] 郑毓信．数学教育视角下的“核心素养”[J]．数学教育学报，2016，25（3）：1-5．

[15] 约翰·杜威．我们怎样思维·经验与教育[M]．姜文闵译．北京：人民教育出版社，2005．

[16] 韩云桥．论数学学习的经验性思维[J]．数学教育学报，2015，24（5）：51-54．

[17] 吴有昌，高凌飚．SOLO分类法在教学评价中的应用[J]．华南师范大学学报（社会科学版），2008，（3）：95-99．

[18] 史宁中．学科核心素养的培养与教学——以数学学科核心素养的培养为例[J]．中小学管理，2017，（1）：35-37．

[19] 黄秦安．我们应该如何认识数学的本质[J]．数学教育学报，2003，12（3）：37-41．

[20] 徐利治．数学方法论选讲[M]．武汉：华中理工大学出版社，2000．

[21] 陈志辉．中美两国初中数学课程的问题情境水平比较研究——以“函数”内容为例[J]．数学教育学报，2016，25（1）：5-9．

Creating Problem Situation: Based on the Development of Thinking in Mathematics

REN Xu, XIA Xiao-gang

(School of Mathematics Science, Guizhou Normal University, Guizhou Guiyang 550001, China)

Problem situation was a kind of thinking and close to the reality of students in mathematics. The core task of creating problem situation in teaching was to transform the relationship between number and form in concept and theorem from the known into the unknown relationship which needed to be thought and explored, as well as put in the realistic background related to students. It score significance lied in stimulating the student’s problem consciousness and triggering students’ mathematical thinking. It attached great importance on discovering problems related to the development of the students’ thinking in the aspects of designing derivative theme, grasping the nature of mathematical content, transforming mathematical relation and clarifying problem structure.

mathematical thinking; problem situation; creating question situation; mathematics teaching

[责任编校：周学智]

G632.0

A

1004–9894（2017）04–0015–04

2017–03–05

贵州省省级本科教学工程项目——数学与应用数学专业卓越教师培养计划（黔教高发[2014]378号）；贵州省省级本科教学工程项目——培养高师数学专业学生“教思辨、教体验、教表达”指导能力的实践研究（黔教高发[2014]378号）；贵州省研究生教育创新计划项目——学科教学（数学）专业学位研究生工作站（黔教研合JYSZ字[2015]003）

任旭（1990—），女，湖南永州人，博士生，主要从事数学教育研究．夏小刚为本文通讯作者．