基于移动平均值滤波的储能容量配置研究
2017-09-08陈佩琳贾成真郭跃年
陈佩琳,贾成真,郭跃年
(1.国网山西省电力公司,山西 太原 030001;2.山西大学自动化系,山西 太原 030013;3.国家电投集团山西新能源有限公司,山西 太原 030006)
电网技术
基于移动平均值滤波的储能容量配置研究
陈佩琳1,贾成真2,郭跃年3
(1.国网山西省电力公司,山西 太原 030001;2.山西大学自动化系,山西 太原 030013;3.国家电投集团山西新能源有限公司,山西 太原 030006)
针对风储容量配比问题,从分析风电场波动特性入手,将波动的动态指标转变为静态指标,研究了风电场的“平滑效应”,进而采用储能集中式布置方式,基于风储协调控制策略,提出了带死区的移动平均值滤波算法,基于正态分布的数学分析方法,依据3σ原理得出储能的额定功率值,依据储能荷电状态设置了合理的储能容量裕度,按照储能连续充放电的最大容量值来确定储能系统的容量,并且在Matlab/Simulink中进行了仿真验证,形成了一种简单且工程实用的风储容量配比估算理论。
移动平均值;正态分布;3σ;容量配比
0 引言
随着风电装机容量在电网中的占比不断增加,而电网的备用装机容量有限,风电消纳已经成为制约风电发展的瓶颈。以山西省为例,由于供热机组装机容量占比较大,到了冬季风电大发,电网调峰形势严峻,导致“弃风”现象的发生,据国家能源局统计,去年山西省的弃风率为9%。
有许多研究从调节风机的桨距角出发来平抑风电的波动,但是对于短期的风功率波动,由于桨距调节的速度比较慢所以达不到平抑波动的要求。随着化学储能成本的降低、大规模化学储能集成控制技术的成熟,化学储能被看成是平抑风电波动的有效途径之一。储能与风电之间的容量配比是近几年来学者们研究的热点。
文献 [1]基于一阶低通滤波原理,采用荷电状态SOC(state of charge) 平衡控制策略减小了系统所需储能容量,文献 [2]从经济调度的角度对风储的容量配置进行了优化,文献 [3]将容量配比与储能SOC控制相结合,通过合理的统计计算得出储能的容量配置,文献 [4]基于自适应线性神经元 (Adaline)原理,采用4步协调控制的方法大大减小了储能的容量配置,文献 [5]提出了一种双层规划模型,通过遗传算法对模型进行求解,得到了全局经济性最优的储能容量配置。上述研究中,大多数学者利用一阶低通滤波来求取储能容量,然而这种方法在风功率波动频繁时容易导致储能的荷电状态超限,而且一阶低通滤波算法平滑后的风功率值存在“滞后”现象,使得到的储能配置容量相对较大;采用多步协调,多层次规划等方法对于储能的容量配置估算太过复杂,不利于工程的实现,所以急需寻找一种简单且工程实用的储能容量配置估算方法。
论文首先分析了风电场波动特性,通过将波动的动态指标转变为静态指标,研究了风电场的“平滑效应”,进而采用储能集中式布置方式;其次,提出了带死区的移动平均值滤波算法,通过风储之间的协调控制,得出储能的充放电功率值,基于正态分布的数学分析方法,依据3σ原理得出储能的额定功率值,依据储能SOC设置了合理的储能容量裕度,按照储能连续充放电的最大容量值来确定储能系统的容量,最后在 Matlab/ Simulink中进行了仿真验证,形成了一种简单且工程实用的风储容量配比方法。
1 风储联合发电系统的结构
目前储能在风场的布置形式主要有2种,如图1和图2所示。
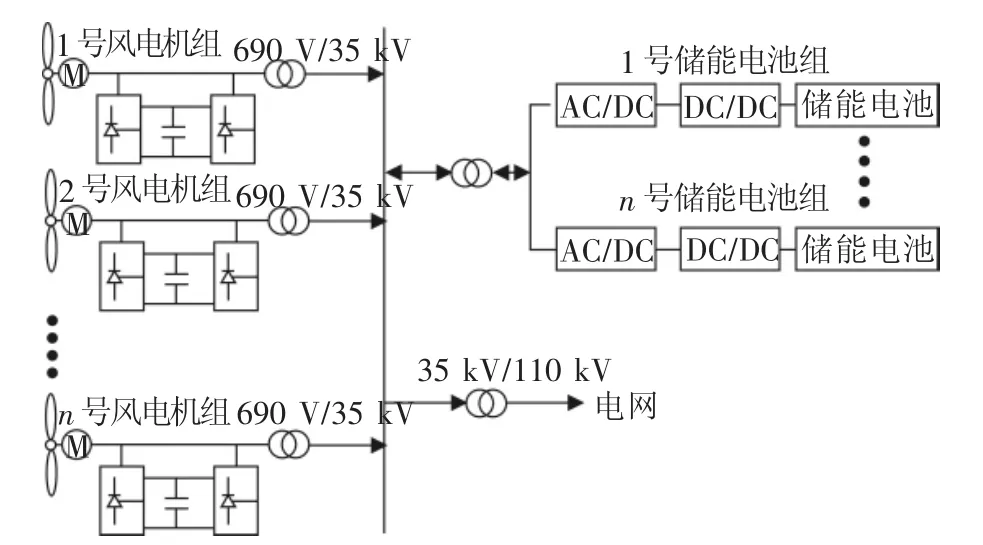
图1 储能集中式布置
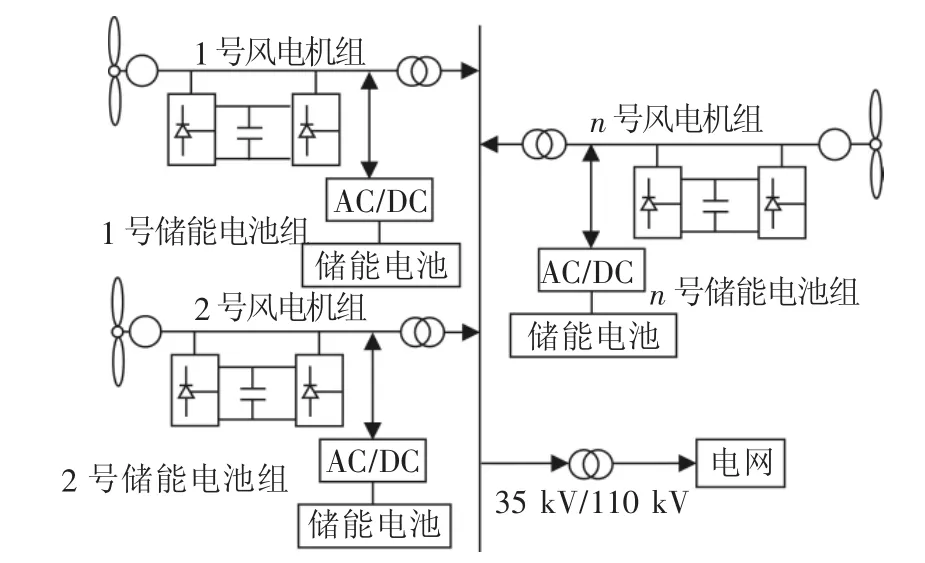
图2 储能分散式布置
图1 中储能采用集中式布置,储能通过DC/ DC、DC/AC两级接入风电场35 kV母线,这种结构实现了风电场各台风电机组广域互补性,在一定程度上减小了储能的容量配置;图2中储能采用分散式布置,该方案从风场的局部出发,通过对风场中各台风机进行平滑控制,从而达到平抑整个风电场功率波动的目的,但是分散式布置使得系统的复杂性增加,对于整个风场来说总的容量要比集中配置储能容量大[6]。
鉴于以上分析,并且根据国家已有风储示范工程项目:张北的风光储输示范工程、辽宁的卧牛石风储示范工程,其采用的是储能集中式布置结构,所以本文选择储能集中式布置的风储联合发电系统结构,从分析风电场整体有功输出波动性入手,来对储能进行容量配置的分析。
2 风功率波动分析和风储协调控制策略
2.1 风电功率波动分析
对于并网风电场来说,其最大功率变化需结合实际电网的调频能力及其他电源调节特性来确定,很难给出一个统一的确定限值,适合于各种电网运行要求[7]。我国关于风电场并网运行时功率最大变化的推荐值如表1所示。

表1 风电场有功功率变化最大限值
经过调研分析可知大部分运行的风电场1 min和10 min功率变化值都满足国家的规定值,所以本文提出通过在风电场配置储能,将风电场输出功率变化值限制在1 min不超过风场装机容量的2%,10 min不超过风场装机容量的7%。
选取山西某一风电场为研究对象,依据风电场测风塔数据可知:风电场年平均风速7.42 m/s,风功率密度465.6 W/m2。该风电场额定装机容量为49.5 MW,有33台1.5 MW的华仪双馈风力发电机组,启动风速3.5 m/s,额定风速13 m/s,切出风速25 m/s,采用功率因数为1的恒功率因数控制方式。选取典型日运行数据,采样时间间隔为30 s,单机输出功率和风电场输出功率如图3和图4所示。
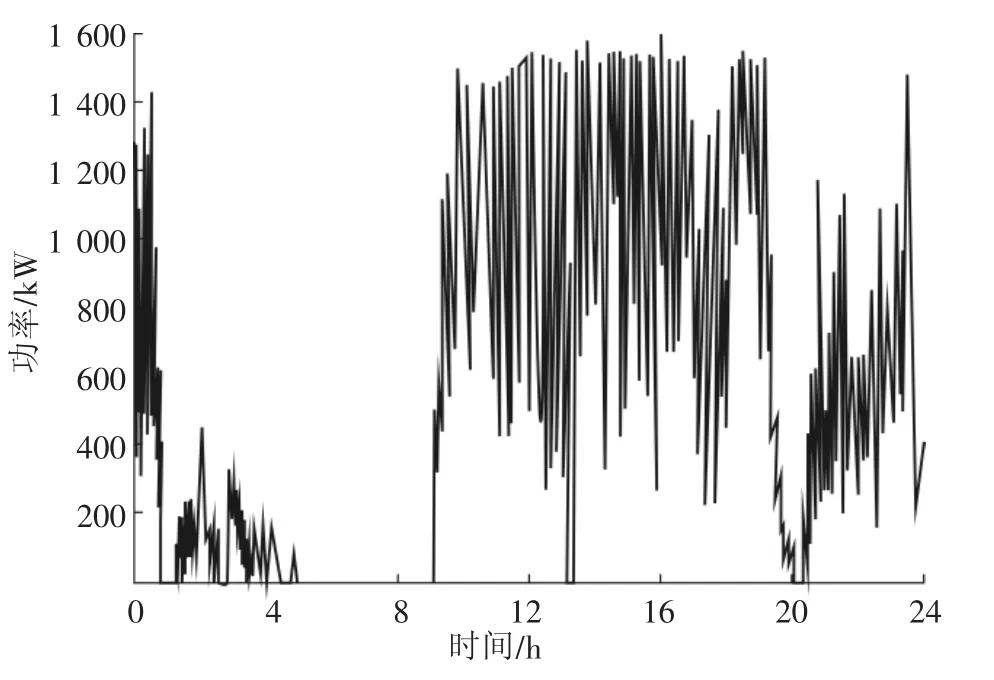
图3 单机输出功率
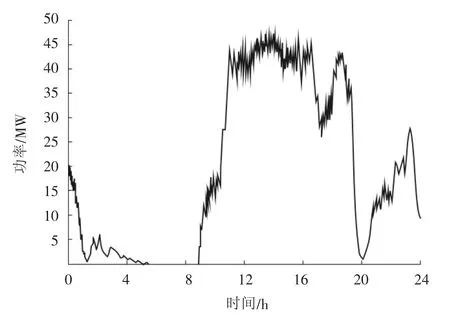
图4 风电场输出功率
比较图3和图4可以得到如下结论:风电功率波动随风电规模的增大存在“平滑效应”[8]。
依据文献[9]提出的5个动态指标对风电功率波动进行分析,具体的指标表达如式(1)—(5)。
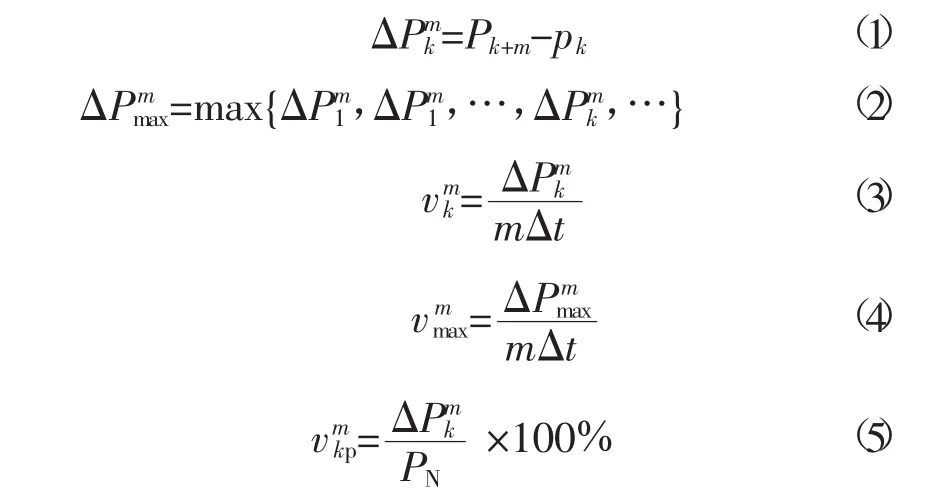
由于动态指标是随时间不断发生变化的,不利于定量分析,所以采用正态分布的统计方法,将动态指标转化为静态指标。表2给出了1 min波动变化率、波动率,10 min波动变化率、波动率和输出功率方差在风机台数分别为1台、10台、20台、33台时的统计指标。
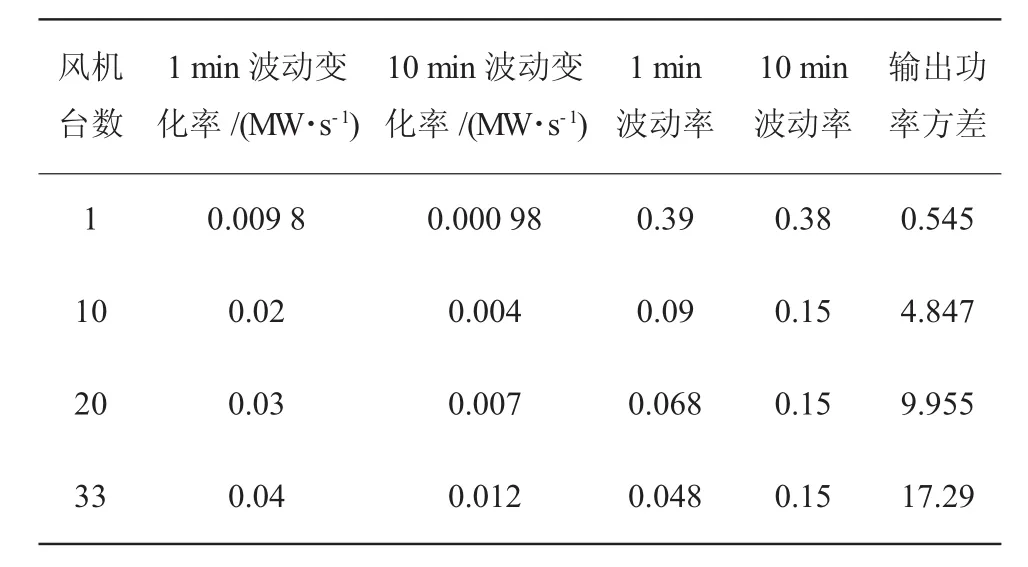
表2 不同风机台数的指标统计值
从表2的统计数据可以看出:无论是1 min还是10 min波动率都随装机容量的增加而呈现递减的趋势,说明了风电场各台风机之间存在互补性;而波动变化率则随容量的增加而呈现递增的趋势,说明风电场装机容量越大,风电对电网的影响越大。
2.2 风储协调控制策略
为了避免一阶低通滤波的“滞后”现象,本文采用带死区的移动平均值滤波算法,其原理如式(6)所示。
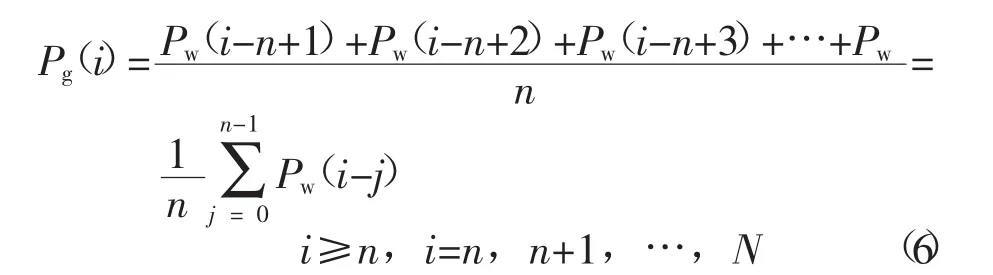
由于本文中采集的风电场数据有限,对于前n-1个数据的平滑采用式(7)进行处理。
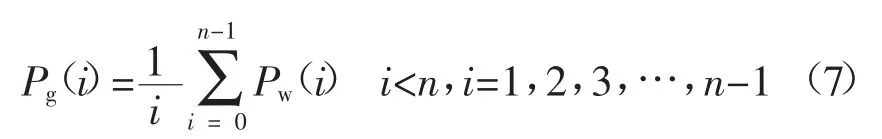
风储并网功率值Pg(i)不是每个时刻都是等于移动平均值平滑过后的值,只有当风电功率Pw(i)不在并网功率带内才需要对其进行平滑。并网功率带按照风电波动的目标值进行设计,本文提出将1 min风功率波动限制在2%以内,所以取移动平均值的±1%作为并网区间。
3 储能容量配比
3.1 3σ原理简介
正态分布又名高斯分布,是一个在数学、物理及工程等领域都非常重要的概率分布。正态分布的曲线特征如图5所示。
在正态分布里,约有99.7%的情况都处于样本μ±3σ这个区间内,其他取值的概率不到0.3%,是几乎不可能发生的小概率事件,μ、σ分别为样本的平均值和标准差。
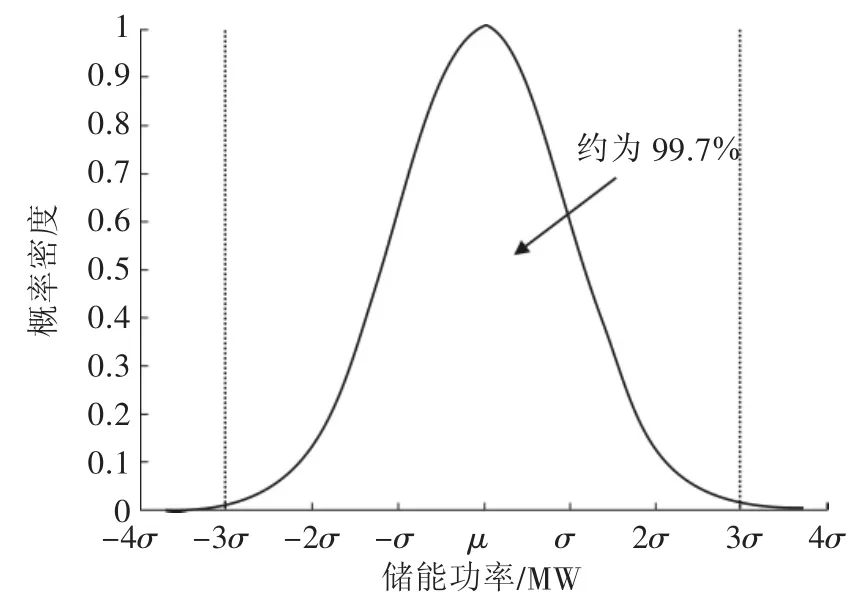
图5 正态分布的概率密度曲线
通过风储协调控制策略得出储能的充放电功率值,依据数学概率统计学的知识,其符合均值为μ,方差为σ的正态分布[10]。μ和σ的表达式如式 (8)—(9)所示。
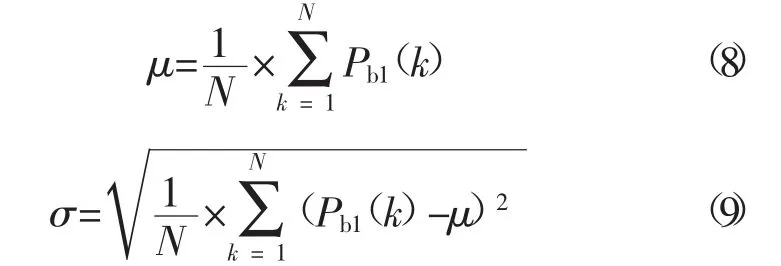
式(8)—(9) 中,N表示采样的样本数量,Pb1(k)表示k时刻储能的充放电功率值。
3.2 储能容量配比计算
取山西某一风电场2016年某一典型日的运行数据,采用带死区的移动平均值滤波算法对其进行平滑处理,得到储能一天的充放电功率值如图6所示。
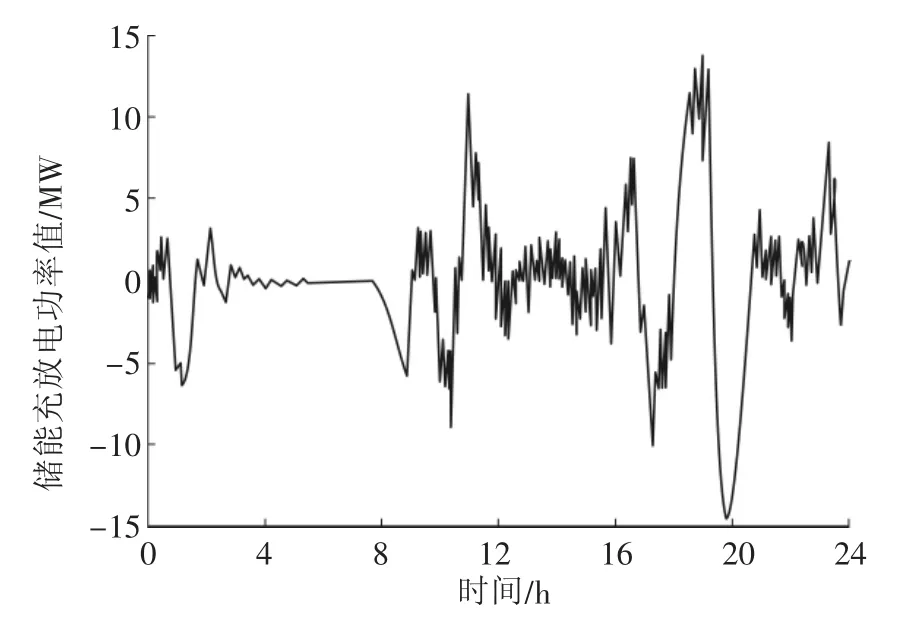
图6 储能充放电功率值
利用Matlab对储能的充放电功率值进行统计计算,得出其平均值μ=-0.08,σ=4.08,按照式(10)确定储能的额定功率值。
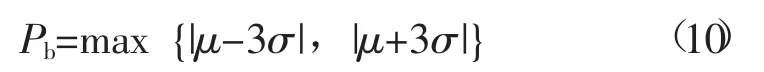
经过计算可以得到Pb=12.32 MW。
对储能的充放电功率值在时间域上进行积分,便可得到储能一天容量的变化。在储能系统实际运行过程中,由于常常考虑储能系统的荷电状态(SOC) 是否越限,本文按照储能SOC值在0.2~0.8的区间内属于储能的合理运行范围,故求取储能的容量按照20%的裕度进行计算,即如式(11)所示。
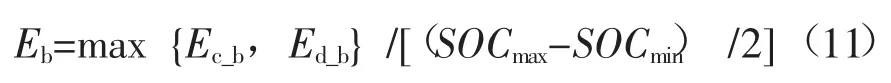
Ec_b和Ed_b分别表示储能的充放电量,SOCmax和SOCmin表示储能SOC的最大值和最小值,经计算可以得到Eb=28.8 MW·h。所以风电场需要配置的储能容量为12 MW/28.8 MW·h。
4 仿真验证
在Matlab/Simulink中建立如图7所示的仿真模型。模型中储能的初始SOC值设为0.5,仿真的采样时间设置为1 s,仿真时长为2 880 s。
按照本文提出的储能容量配置,风储联合发电系统运行中储能系统的SOC变化曲线如图8所示。图中储能SOC的最小值为0.2,最大值为0.68,能够保证储能SOC值运行在合理的工作区间。
在风电场中配置储能,通过风储之间的协调控制,降低了风电场输出功率的波动性,能够把波动率限制在本文所要求的指标内。图9具体给出了风储联合输出功率的波动率曲线。
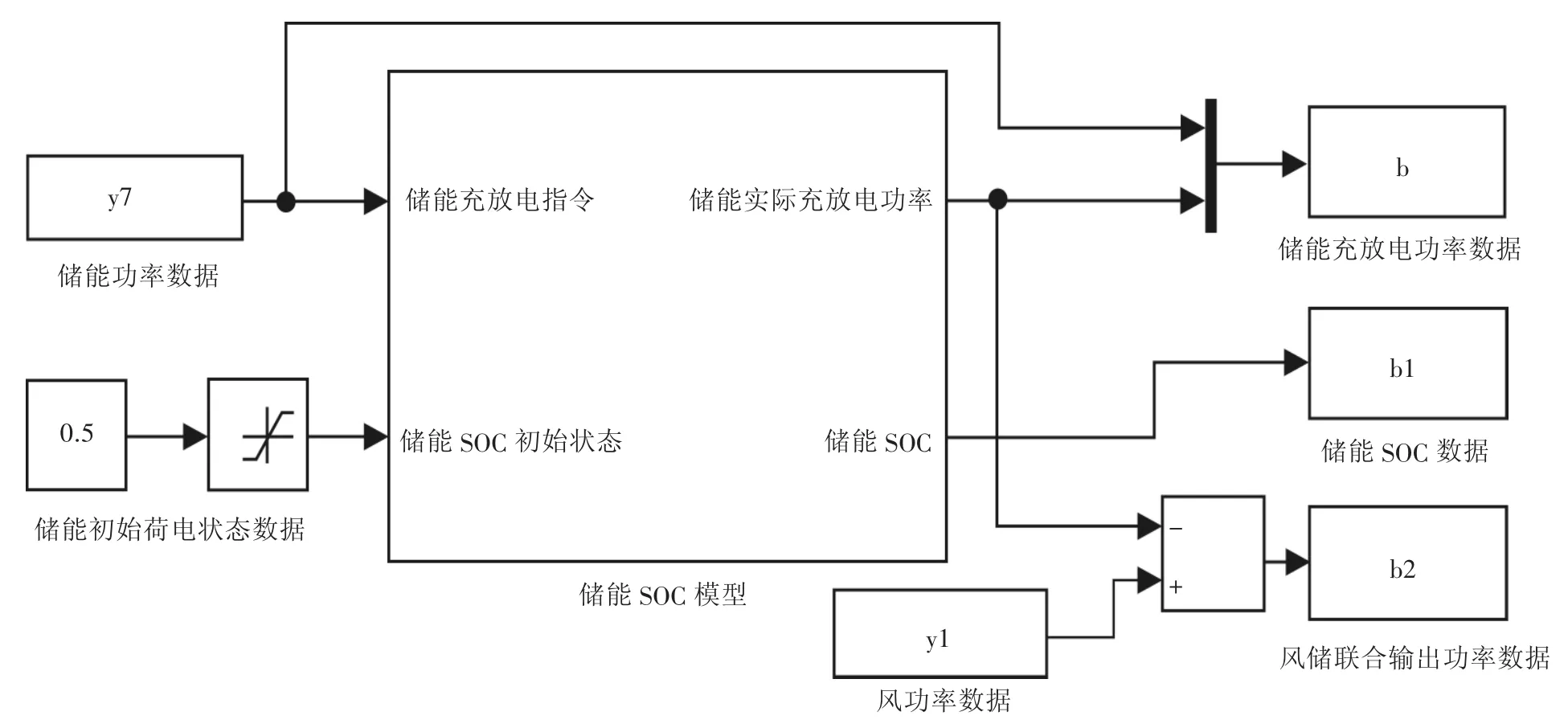
图7 储能SOC仿真图
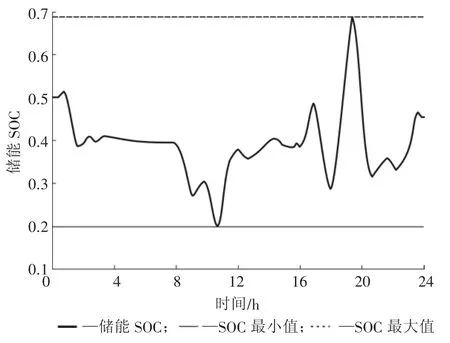
图8 储能SOC变化曲线
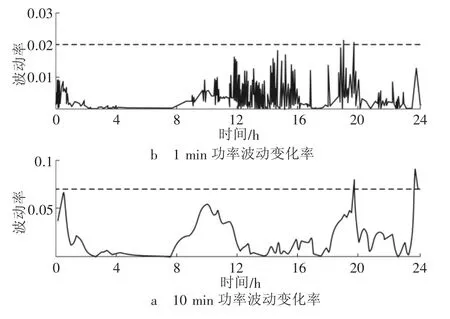
图9 风储功率波动率曲线图
移动平均值滤波算法中移动平均的项数决定了平抑过后的风功率波动的大小,也决定了储能容量配置,本文选取的移动平均值项数为300,满足了1 min和10 min波动率指标要求。
5 结论
本文依托山西某一风电场实际运行数据,对风电场出力的波动性进行了分析,通过对单台风机到10台、20台、33台风机运行数据的统计分析得出风电场在空间上的“平滑效应”。采用带有死区的移动平均值滤波算法,基于数学统计的方法得出储能的估算容量配置,其原理简单且工程实用。
[1] 时珊珊,蔡旭,欧阳曾恺,等.风储联合运行的储能容量优化选配算法及分析 [J].电器与能效管理技术,2015,12(8): 39-44.
[2] 殷志敏,晁勤,王纯琦,等.基于风储经济调度的储能容量优化配置 [J].可再生能源,2016,34(1):64-71.
[3] AbdelkaderAbbassi,MohamedAliDami,MohamedJemli.Astatistical approach for hybrid energy storage system sizing based on capacity distributionsinanautonomousPV/Windpowergenerationsystem[J]. RenewableEnergy,2017(103):81-93.
[4] M.Jannati a,S.H.Hosseinian b,B.Vahidi b,Guo-jie Li.ADALINE (ADAptive Linear NEuron)-based coordinated control for wind power fluctuations smoothing with reduced BESS(battery energy storage system)capacity[J].Energy,2016(101):1-8.
[5] 袁铁江,蒋平,孙谊媊,等.风储一体化电站容量双层优化规划研究 [J].高电压技术,2015,41(10):3204-3212.
[6] 姜书鹏.风储联合发电系统容量配比优化及其技术经济性研究 [D].吉林:东北电力大学,2013.
[7] 中国电力科学研究院.风电场接入电力系统技术规定:GB/T 19963-2011[S].北京:中国电力出版社,2011.
[8] 崔杨,穆钢,刘玉,等.风电功率波动的时空分布特性 [J].电网技术,2011,35(2):110-114.
[9] 李军徽.抑制风电对电网影响的储能系统优化配置及控制研究 [D].北京:华北电力大学,2012.
[10] 靳文涛,李建林.电池储能系统用于风电功率部分“削峰填谷”控制及容量配置 [J].中国电力,2013,46(8):16-21.
Research on Energy Storage Capacity Distribution Based on Moving Average Filter
CHEN Peilin1,JIA Chengzhen2,GUO Yuenian3
(1.State Grid Shanxi Electric Power Corporation,Taiyuan,Shanxi030001,China;2.Department of Automation,Shanxi University,Taiyuan,Shanxi030013,China;3.SPIC Shanxi New Energy Co.,Ltd.,Taiyuan,Shanxi030006,China)
In view of wind storage capacity ratio,the wind power fluctuation characteristics are analyzed.The dynamic fluctuation indexis transformed intostatic index,which verifies the"smooth effect"ofwind farm.Based on wind storage coordination controlling,BESS centralized arrangement is adopted,and a dead zone average filtering algorithm strategy is proposed.Based on the analysis of normal distribution and accordingto3σ,the storage rated power value is determined.Accordingto the storage state ofcharge(SOC),a reasonable storage capacity margin is set up.The storage capacity of the system is determined according to the maximum continuous charge and discharge capacity,and the simulation is conducted in the Matlab/Simulink,finally,a simple and practical wind storage capacity ratio estimation theoryis formed.
movingaverage;normal distribution;3σ;capacityratio
TM714;TM76
A
1671-0320(2017)04-0001-05
2017-05-04,
2017-05-19
陈佩琳(1960),女,湖南长沙人,1982年毕业于太原工业学院继电保护专业,高级工程师,从事电网调度方面的研究;
贾成真(1989),男,河南安阳人,山西大学自动化系2015级硕士研究生在读,从事风储协调控制方面的研究;
郭跃年(1971),男,山西山阴人,1993年毕业于太原工业大学热能动力专业,高级工程师,从事新能源并网方面的研究。
