基于二次指数平滑法的典型城市电气火灾预测
2017-09-08刘义祥
汤 昊,金 静,刘义祥,许 洁,贾 南
(武警学院,河北 廊坊 065000)
●消防安全评价
基于二次指数平滑法的典型城市电气火灾预测
汤 昊,金 静,刘义祥,许 洁,贾 南
(武警学院,河北 廊坊 065000)
针对电气火灾发展现状,结合二次指数平滑法适用于短期预测的特点,以近期北京市、重庆市的相关数据为研究对象,运用二次指数平滑法建立电气火灾预测模型,对两地2015、2016年电气火灾起数进行了预测,并将2015年的预测值与实际值进行了比对。结果表明,二次指数平滑法对典型城市电气火灾短期预测具有可行性,预测结果可为电气火灾的防控提供参考。
二次指数平滑法;电气火灾;火灾预测
0 引言
目前我国已成为世界第二大经济体,工业与居民用电量持续保持在较高水平,由此也使得电气故障引发的火灾事故在总火灾起数中占有较大比例。据统计,近几年我国电气火灾占总火灾起数的30%以上,特别是在重特大火灾中,电气火灾占比高达50%。在数据化、信息化越来越普及的今天,电气火灾的预测将为消防工作提供参考,并有助于减少电气火灾所造成的人员伤亡与财产损失。目前,国内学者对相关领域的研究可大致归为两类,一是针对电气火灾的发生特点,对典型案例进行分析,并从宏观上提出相应对策;二是基于各项火灾数据的统计、整理与分析,并得出防范措施。在火灾数据的整理与统计方面,logistic回归、灰色系统、马尔可夫模型、聚类分析、神经网络、时间序列及相关性分析等是常用的数学方法。刘海生等人利用主成分分析与灰色系统对全国的火灾形势进行了综合评价与预测[1];李杰通过聚类分析对北京市的火灾事故做出了统计与分析[2];田树仁则通过神经网络设计了电气火灾的预警方法[3]。而二次指数平滑法作为基于时间序列的一种分析方法,在短期预测中具有直观便捷、易于操作的优势,并在其他领域作为一种重要的分析方法被广泛应用。王洪德等人通过三次指数平滑法对我国近几年的道路交通事故的死亡人数做出了预测[4];何大四等人则通过指数平滑法对空调负荷进行了预测[5];朱奕奕等人利用指数平滑法对上海市甲型病毒性肝炎的发病趋势做出预测[6]。由于指数平滑法具有跟踪时序进行非线性趋势模拟的特点,将其应用于电气火灾发生次数的预测具有一定可行性[7]。本文基于2010—2016《中国消防年鉴》中电气火灾部分数据,以北京、重庆为例,通过二次指数平滑法预测电气火灾。
1 研究方法
1.1 二次指数平滑法
指数平滑法(Exponential Smoothing,ES)是由布朗(Robert G.Brown)提出,他认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;而且最近的发展态势,在某种程度上会持续一段时间,所以将较大的权数放在最近的数据中[8-10];并且在实际生活中,指数平滑法经常用于中短期经济发展趋势的预测[11]。本文所采用的二次指数平滑法不能单独进行预测,它必须与一次指数平滑法配合,建立预测的数学模型,然后运用数学模型确定预测值。线性二次指数平滑法只利用三个数据和一个平滑系数就可进行计算,其方便快捷的优势体现的较为明显,因而在大多数情况下,线性二次指数平滑法是应用范围更广的预测方法[12-13]。
1.2 二次指数平滑法预测公式
二次指数平滑法是对一次指数平滑值再作一次指数平滑的方法。其预测公式为:

式中,Yt+T为预测值;T为预测超前期数;at、bt为预测参数,t=1,2,3,…,n(n为原始数据的个数)。
2 实例分析
火灾统计的各项数据包括:火灾起数、死亡人数、受伤人数、直接财产损失、烧毁建筑面积、受灾户数,在这些数据中,火灾起数可以比较宏观分析火灾形势,也能直观体现某地域的电气火灾发生概率,因此选取北京、重庆电气火灾起数作为主要预测参数。
2.1 数据来源
应用二次指数平滑法时,一般近期数据所占权重较大,因此选取最近7年北京、重庆两地的电气火灾发生起数,共14个数据,如图1所示。从图中可以看出,数据在2011至2012年出现了较大波动,因此可以在一次指数平滑的基础上再进行一次指数平滑,以减小产生的误差。
2.2 数据的选取
两组数据各含7个数据,并将2015年的数据用于检验预测的可行性,故使用2009—2014年的数据作为数据样本,并将初始年份(2009年)的数据作为初始值。
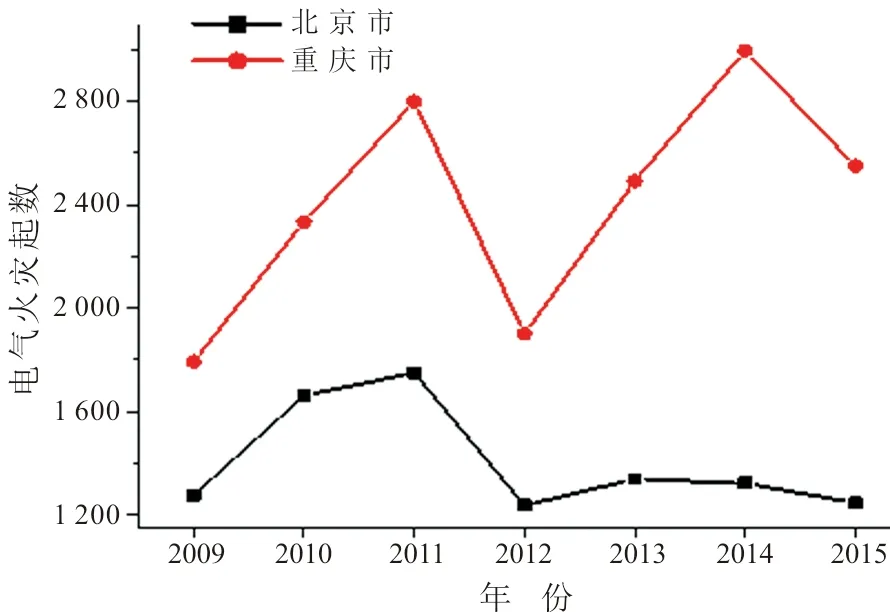
图1 北京、重庆电气火灾起数
指数平滑法的计算中,关键是α的取值大小,但α的取值又容易受主观影响,因此合理确定α的取值方法十分重要。一般来说,如果数据波动较大,α值应取大一些,可以增加近期数据对预测结果的影响。如果数据波动平稳,α值应取小一些。具体如下:(1)当时间序列呈现较稳定的水平趋势时,应选较小的α值,一般在0.05~0.2之间取值;(2)当时间序列有波动,但长期趋势变化不大时,可选稍大的α值,常在0.1~0.4之间取值;(3)当时间序列波动很大,长期趋势变化幅度较大,呈现明显且迅速的上升或下降趋势时,宜选择较大的α值,可在0.6~0.8间选值,以使预测模型灵敏度高些,能迅速跟上数据的变化;(4)当时间序列数据是上升(或下降)的发展趋势类型,α应取较大的值,在0.6~1之间。
由图1可知,北京市在2009—2015年电气火灾发生起数的变化不大,因此将α初步选定在0.05~0.2之间,选取α值为0.05,0.1,0.2并对结果分别进行预测,由于三组预测值与实际火灾起数均相差不大,故计算出α在取不同值时预测值与原始数据的相对误差,结果如图2。由图2可知,当α=0.2时,计算所得出的相对误差较小,分析结果较为准确,故在预测北京市电气火灾发生起数时,α取0.2。
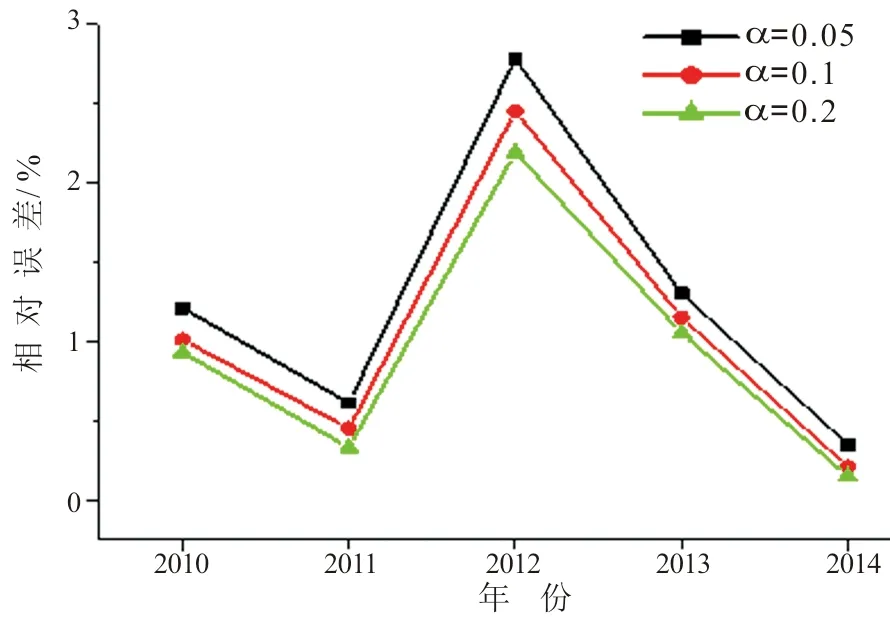
图2 α值不同时北京市电气火灾起数预测所产生的相对误差
由图1可知,重庆市在2009—2014年电气火灾发生起数的变化相对较大,因此将α初步选定在0.4~0.6之间,选取α值为0.4,0.5,0.6并对结果分别进行预测,由于三组预测值与实际火灾起数均相差不大,故计算出α取不同值时预测值与原始数据的相对误差,结果如图3。由图3可知,当α=0.6时,计算所得出的相对误差较小,分析结果较为准确,故在预测重庆市电气火灾发生起数时,α取0.6。

图3 α值不同时重庆市电气火灾起数预测所产生的相对误差
2.3 预测结果
将初始值代到公式(1)~(4)中,并通过选定的平滑系数进行计算,求出各个预测参数,经计算,a北京2014=1319.015,b北京2014=-1.238,故Y北京2014+T=1319.015-1.238T,将T=1,2代入,可得到北京市2015、2016年电气火灾起数的预测值,见表1。比对2010—2015年预测值与实际值,见图4,可以发现预测值与实际值大致相符,并结合最新数据进行检验,2015年北京市电气火灾预测值与实际值相对误差为5.9%。由此看出,通过该方法所做出的短期预测相对准确。不难看出,北京市电气火灾起数自2012年起呈现相对稳定的发展趋势,虽然其用电量大、人口密集,但消防监管力度较大,相关宣传活动开展较好,故北京市电气火灾发生起数将在短期内比较稳定。因此,该地区需继续保持火灾的防治、监管、宣传力度,在控制电气火灾发生起数的前提下进一步减少人员伤亡与财产损失。

表1 北京市2010—2016年电气火灾起数预测

图4 北京市实际值与预测值趋势对比
同样,经计算,a重庆2014=2812.43,b重庆2014=143.718,故Y重庆2014+T=2812.43+143.718T,将T=1,2代入,可以得到重庆市2015、2016年电气火灾起数的预测值,见表2。比对2010—2015年预测值与实际值,见图5,可见预测值与实际值略有误差。并结合最新数据进行检验,2015年重庆市电气火灾实际值与预测值相对误差为15.9%。但不难看出,重庆市电气火灾起数总体数量偏高,除2012年电气火灾数目大幅下降以外,近几年又逐渐恢复至2 800起左右,并在短期内呈现递增趋势。因此,该地区需进一步加强火灾的防治、监管、宣传力度,总结并吸取2012年的相关经验,逐渐控制电气火灾发生起数,以减少由此引发的人员伤亡及财产损失。
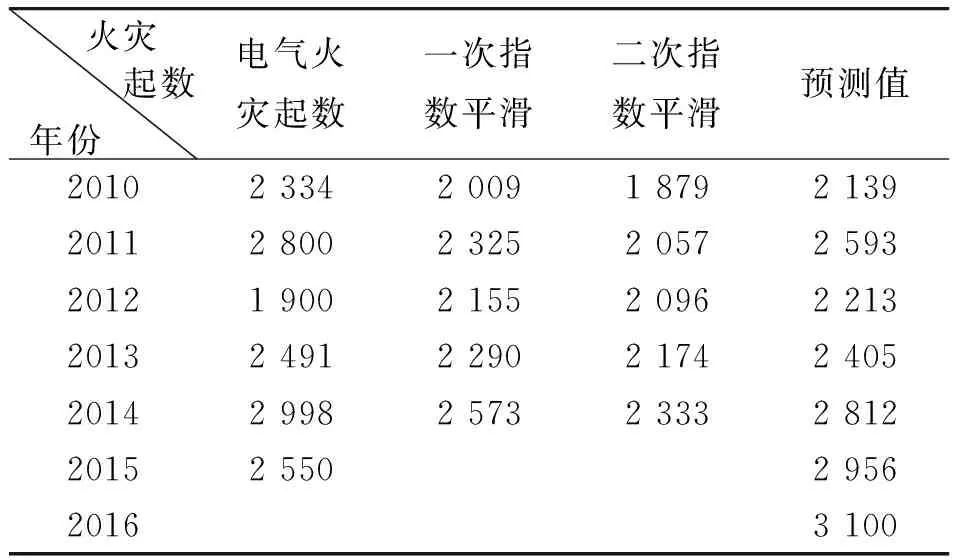
表2 重庆市2010—2016年电气火灾发生起数预测
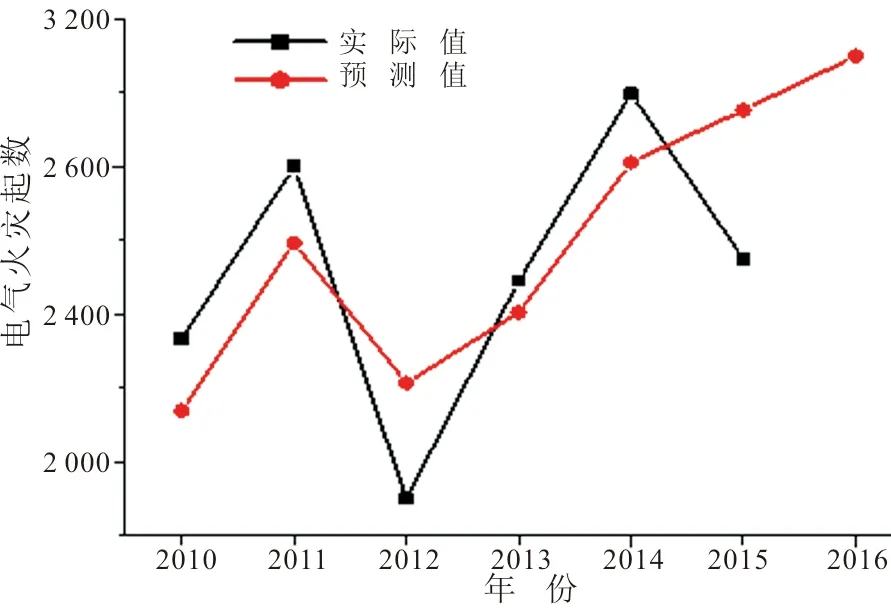
图5 重庆市实际值与预测值趋势对比
通过数据分析可以发现,二次指数平滑法是基于近期数据进行预测的一种方法,若数据随时间推移所产生的变化幅度较大,则预测结果与实际火灾发生起数的误差就会偏高,因此该方法较适用于近期火灾起数变化幅度较小地区的火灾预测,进而达到控制误差,准确预测的效果。
3 结论
本文结合电气火灾发展现状,通过二次指数平滑法分别对北京市、重庆市2015、2016年的电气火灾起数进行了预测,得出北京市在2015、2016年的电气火灾起数分别为1 318起、1 317起;重庆市在2015、2016年的电气火灾起数分别为2 956起、3 100起。依据2015年两地电气火灾起数进行检验,得出二次指数平滑法在电气火灾的短期预测中具有可行性,并依此对电气火灾防控提出了建议。
[1] 刘海生,张鑫磊,宋丽霞.基于统计数据的全国火灾形势综合评价与预测[J].中国安全科学学报,2011,21(6):54-59.
[2] 李杰.北京市火灾事故特征的统计分析[J].中国安全生产科学技术,2013,9(5):126-130.
[3] 田树仁.基于神经网络的智能电气火灾预警系统设计[J].消防科学与技术,2015,34(9):1201-1204.
[4] 王洪德,曹英浩.道路交通事故的三次指数平滑预测法[J].辽宁工程技术大学学报,2014,33(1):42-46.
[5] 何大四,张旭.改进的季节性指数平滑法预测空调负荷分析[J].同济大学学报,2005,33(12):1672-1676.
[6] 朱奕奕,赵琦,冯玮,等.应用指数平滑法预测上海市甲型病毒性肝炎发病趋势[J].中国卫生统计,2013,30(1):31-36.
[7] 叶宗斌,周步祥,林楠,等.基于等维新息指数平滑法模型的中长期负荷预测[J].电力系统保护与控制,2012,40(18):47-51.
[8] 刘造保,徐卫亚,张开普,等.基于改进指数平滑法的岩体边坡变形预测[J].河海大学学报,2009,37(3):313-316.
[9] 安振宇,陈云国.基于火灾统计数据的火灾形势综合评价和定量预测[J].中国安全生产科学技术,2006,2(2):29-33.
[10] 芮海田,吴群琪,袁华智,等.基于指数平滑法和马尔科夫模型的公路客运量预测方法[J].交通运输工程学报,2013,13(4):87-93.
[11] 李贵仁,李飞跃,丁万君.用数理统计方法对未来火灾形势的预测分析[J].消防科学与技术,2005,24(6):765-768.
[12] 胡巍,常金源,李祥龙,等.指数平滑法预测滑坡变形的适用性讨论[J].人民长江,2015,46(14):28-31.
[13] 郭璐,张敏,朱万平,等.指数平滑法在南京市艾滋病疫情预测中的应用[J].中国艾滋病性病,2014,20(12):914-921.
(责任编辑 马 龙)
Prediction of Electrical Fires in Typical Cities Based on Exponential Smoothing Method
TANG Hao, JIN Jing, LIU Yixiang, XU Jie, JIA Nan
(The Armed Police Academy, Langfang, Hebei Province 065000, China)
Based on the status quo of electrical fires and the features of exponential smoothing method, this paper analyzes the electrical fire data of Beijing and Chongqing, and establishes a fire prediction model with the exponential smoothing method, in order to forecast the number of electrical fires in 2015 and 2016, and compare the predicted values with the actual values in 2015. The results show that the exponential smoothing method is feasible for short-term prediction of electrical fires in typical cities, providing a reference for the prevention and control of electrical fires.
exponential smoothing method; electrical fire; fire prediction
2017-03-30
河北省科技计划项目(16215416);河北省统计科学研究计划项目(2016HY11)
汤昊(1994— ),男,黑龙江黑河人,在读硕士研究生; 金静(1986— ),女,安徽萧县人,讲师,博士; 刘义祥(1970— ),男,河北南皮人,教授; 许洁(1983— ),女,河北廊坊人,讲师; 贾南(1987— ),男,河北廊坊人,讲师。
D631.6
A
1008-2077(2017)08-0063-04
