近距平行跑道配对进近纵向碰撞风险安全评估

王健，张兆宁，卢飞

(中国民航大学 国家空管运行安全技术重点实验室，天津 300300)

近距平行跑道配对进近纵向碰撞风险安全评估

王健，张兆宁，卢飞

(中国民航大学 国家空管运行安全技术重点实验室，天津 300300)

针对繁忙机场的容量饱和现象，近距平行跑道实施配对进近可有效提高机场容量、缓解跑道拥挤和航班延误等现象。为了保证配对进近的安全运行，根据近距平行跑道配对进近的实际运动过程，考虑两架飞机在配对进近过程中的导航误差和时间等因素，建立两架飞机的运动方程和纵向碰撞风险评估模型；并通过MATLAB软件对模型进行计算，得到随相关参数变化的纵向碰撞风险变化曲线。结果表明：配对进近的碰撞风险随着前后两机起始间隔的增大而减小，随着飞机纵向定位误差的均方差的增大而增大，证明了模型的正确性和合理性。

配对进近；碰撞风险模型；近距平行跑道；导航误差

0 引 言

随着我国民航业的快速发展，机场拥堵状况越发严重，一些繁忙机场正面临着严重的容量饱和。增修跑道是目前解决机场客货运输量巨大问题的主要途径。机场修建的多跑道的分布位置种类很多，其中以平行跑道居多。近距平行跑道是指两条跑道中心线平行或跑道中心线夹角小于15°的非交叉跑道，且跑道中心线之间的距离小于762 m的跑道对。国外许多大型机场均已运行近距平行跑道，例如美国亚特兰大哈兹菲尔德-杰克逊国际机场、德国法兰克福国际机场等；而在国内，上海浦东国际机场、上海虹桥国际机场等航空枢纽机场也已运行近距平行跑道。现阶段，我国近距平行跑道的运行方式为隔离平行运行模式，即一条跑道主要用于起飞，另一条主要用于降落。但这种运行模式并未充分发挥近距平行跑道的优势，使得近距平行跑道的运行效率大幅降低，不仅未能解决机场大量航班延误的问题，还会影响高空管制区域及其他机场的正常运行。

美国的Rocky Stone提出了配对进近的思想，即两架飞机在具有IFR规定的间隔情况下同时进行平行进近。在整个配对进近过程中，主要由后机的飞行员对两机的安全间隔负责，后机的飞行员必须注意两个问题：①后机必须和前机保持足够的间距，使得前机闯入后，后机能够执行避让；②后机还必须离前机足够近，以避开前机尾流的影响。以防撞限制确定的最小间隔为前界，以尾流限制确定的最大间隔为后界，所形成的区域称为配对进近安全区。最初提出的配对进近思想是两机的进近航迹完全平行，但随着对尾流影响研究的逐渐深入，发现平行航迹不利于后机避开前机的尾流，并提出了3°偏角配对进近思想。3°偏角配对进近是指后机的进近航道在距离跑道入口约3/4 n mile处有相对于跑道中心延长线3°的偏离。

国外首先对近距平行跑道配对进近方式展开研究。2000年，J.Hammer[1]提出了近距平行跑道配对进近的概念，并分析了配对进近过程中前机对后机的影响；S.Landry等[2]对近距平行跑道配对进近安全区域进行了研究并建立了模型；R.Teo等[3]对配对进近危险区域进行了研究；D.C.Burnham等[4]研究了侧风情况下尾流对近距平行跑道配对进近的影响；R.R.Eftekari等[5]考虑尾流对近距平行跑道配对进近的影响，分析了近距平行跑道实施配对进近的可能性。国内，胡明华等[6]对近距平行跑道进近方法进行了研究；张秀辉[7]对平行跑道安全间隔进行了研究；郑少行等[8]考虑了配对进近运行模式下近距平行跑道的容量问题；吕宗平等[9]基于事故树分析法分析了配对进近的风险；卢飞等[10]对近距平行跑道纵向碰撞风险进行了研究并建立了数学模型；牛夏蕾等[11]对近距平行跑道配对进近最小跟驰距离进行分析，但研究并不深入。

本文主要研究配对进近过程中前机沿直线航向道进近、后机以3°偏角进近的运动过程。假设前机由于导航设备或人为操作误差致使航迹偏转并误入后机进近航迹，导致发生危险接近的情况，建立配对进近两机的纵向距离关于偏转时刻变化的方程；通过MATLAB软件，研究纵向碰撞风险在偏转角度、距跑道端距离、跑道间距等不同参数影响下的变化曲线，并分析纵向碰撞风险的影响因素。

1 模型建立

基于飞机定位误差，根据近距平行跑道配对进近的实际情况，建立近距平行跑道配对进近纵向碰撞风险评估模型。

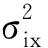
配对进近过程中，不允许出现后机超越前机的情况，且两架飞机之间的纵向距离必须保持足够远，这样即使前机发生偏转后，两机仍然能够保持符合安全目标水平的碰撞风险。根据Reich模型的碰撞模板理念，假设侧向和垂直方向上的间隔为0，纵向发生碰撞的区域为l1≤X1(t)-X2(t)≤l2，则纵向碰撞风险模型为

PX=P{l1≤X1(t)-X2(t)≤l2}

(1)

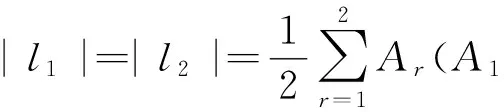
在近距平行跑道配对进近过程中，当准备实施配对进近的飞行员接到管制员指令后，开始实施配对进近，前机以速度V1i飞跃最后进近定位点并减速至V1f，随后匀速飞至跑道入口处；而后机一开始在前机最后进近定位点之外匀速飞行，到达最终进近定位点处开始减速，随后匀速飞行。飞行示意图如图1所示。在整个配对进近过程中，安全间隔由后机飞行员负责时刻保持，以防与前机发生碰撞。

设Xi(t)和Yi(t)分别代表两架飞机t时刻的水平位置，如图1所示。设开始实施配对进近的时刻为初始时刻，该时刻前机位置为原点坐标，由于导航误差等原因影响，前机在t=t0时刻开始向后机航向道闯入，在t=t0+Tturn时刻发现无法再回到原航向，只能以φ度角实施复飞，在此过程中，后机以3°偏角实施进近。

图1 3°偏角配对进近平面坐标图

由于前、后机的机型，以及二者在进近过程中的速度、加速度不同，致使进近过程中的运动方程可分为以下两种情况：

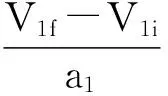
由于导航误差以及飞行员的反应时间等因素的影响，使得飞机在飞行过程中偏离航向道的角度过大，无法恢复到原先的航向，只能选择复飞，在前机穿越后机航向道时，两机具有最大纵向碰撞风险。设偏转完成后直至前机穿越后机航向道的时间间隔为ΔT，在这段时间产生的距离差为ΔX，则：

(2)

(3)

前机在不同时间段发生偏转时两机的纵向间距Lx(t)=X1(t)-X2(t)为

(4)

其中，

t=t0+Tturn

设偏转完成后直至前机穿越后机航向道的时间间隔为ΔT′，在这段时间产生的距离差为ΔX′，则：

(5)

(6)

前机在不同时间段发生偏转时两机的纵向间距Lx(t)=X1(t)-X2(t)为

(7)

其中，

2 算例分析

某机场进行近距平行跑道配对进近，其最终进近定位点与跑道入口的距离为10 000m，后机由3°偏角进近变为沿跑道中心延长线进近的位置距离跑道入口3/4nmile，即1 389m。在其他参数因子均已知的情况下，以前后两机的起始间隔和飞机纵向定位误差的均方差为变量，考虑配对进近纵向碰撞风险随该参数因子变化的情况。

目前，我国近距平行跑道只能当作一条跑道使用，配对进近并未真正实施，因此模型中的参数无法根据配对进近的实际数据准确给出，本文参照非配对进近的相关参数[12]，取前机为重型机，后机为中型机，给出配对进近的相关参数如表1～表2所示。评估从开始实施配对进近到前机到达跑道入口处时两架配对飞机之间的纵向碰撞风险。

表1 配对进近飞机性能参数

表2 配对进近的其他相关参数

2.1 以前后两机的起始间隔为变量

取前后两机的起始安全间隔分别为800、1 000和1 200m，经过MATLAB编程计算，结果如图2所示。

图2 起始间隔对飞机纵向碰撞风险的影响

从图2可以看出：配对进近碰撞风险的概率随着时间的增大而逐渐增大，在前机到达跑道入口时达到最大，且碰撞风险随着起始安全间隔的增大而减小，与实际情况相符。

2.2 以飞机纵向定位误差的均方差为变量

令σ1x和σ2x的值相同，分别为40、50和60，取前后两机的起始间隔为1 000m，其他参数不变，经过MATLAB编程计算，结果如图3所示。

图3 纵向定位误差的均方差对飞机纵向碰撞风险的影响

从图3可以看出：配对进近碰撞风险的概率随着时间的增大而逐渐增大，在前机到达跑道入口时达到最大，且碰撞风险随着飞机纵向定位误差的增大而增大，与实际相符，表明模型是正确、合理的。

3 结 论

本文根据近距平行跑道配对进近的实际运动过程，考虑两架飞机在配对进近过程中的导航误差和时间等因素，建立了两架飞机的运动方程和纵向碰撞风险评估模型。

配对进近碰撞风险的概率随着时间的增大而增大，随着起始安全间隔的增大而减小，随着飞机纵向定位误差的均方差增大而增大。

[1]HammerJ.Casestudyofpairedapproachproceduretocloselyspacedparallelrunways[J].AirTrafficControlQuarterly, 2000, 8(3): 223-252.

[2]LandryS,PrichettAR.Thesafezoneforpairedcloselyspacedparallelapproaches:implicationsforproceduresandautomation[C].DigitalAvionicsSystemsConference, 2000: 7-13.

[3]TeoR,TomlinCJ.Computingdangerzonesforprovablysafecloselyspacedparallelapproaches[J].JournalofGuidanceControlandDynamics, 2003, 26(3): 434-442.

[4]BurnhamDC,HallockJN,GreeneGC.Waketurbulencelimitsonpairedapproachestoparallelrunways[J].Journalofaircraft, 2002, 39(4): 630-637.

[5]EftekariRR,HammerJB,HavensDA,etal.Feasibilityanalysesforpairedapproachproceduresforcloselyspacedparallelrunways[C].IntegratedCommunications,NavigationandSurveilanceConference(ICNS), 2011: 1-14.

[6] 胡明华, 田勇, 李凯. 机场近距平行跑道进近方法研究[J]. 交通运输工程与信息学报, 2003, 1(1): 64-69.HuMinghua,TianYong,LiKai.Studyofapproachproceduretocloselyspacedparallelrunways[J].JournalofTransportationEngineeringandInformation, 2003, 1(1): 64-69.(inChinese)

[7] 张秀辉. 平行跑道安全间隔评估模型研究[D]. 天津: 中国民航大学, 2008.ZhangXiuhui.Thestudyofsafetyintervalevaluationmodelforparallelrunways[D].Tianjin:CivilAviationUniversityofChina, 2008.(inChinese)

[8] 郑少行, 张兆宁. 配对进近运行模式下近距平行跑道容量研究[J]. 航空计算技术, 2013, 43(4): 30-33.ZhengShaohang,ZhangZhaoning.Researchoncapacityofcloselyspacedparallelrunwaysbasedonpairedapproachoperationmode[J].AeronauticalComputingTechnique,2013, 43(4): 30-33.(inChinese)

[9] 吕宗平, 李燕飞, 张兆宁. 基于事故树分析法的配对进近风险分析研究[J]. 科技和产业, 2013, 13(4): 130-134.LüZongping,LiYanfei,ZhangZhaoning.Researchoncollisionriskforpairedapproachbasedonfaulttreeanalysismethod[J].ScienceTechnologyandIndustry, 2013, 13(4): 130-134.(inChinese)

[10] 卢飞， 张兆宁, 魏志强， 等. 近距平行跑道配对进近纵向碰撞风险安全评估[J]. 中国安全科学学报， 2013， 23(8): 108-113.LuFei,ZhangZhaoning,WeiZhiqiang,etal.Thelongitudinalcollisionsafetyassessmentofclosedspacedparallelrunwayspairedapproach[J].ChinaSafetyScienceJournal, 2013, 23(8): 108-113.(inChinese)

[11] 牛夏蕾, 吕宗平, 张兆宁. 近距平行跑道配对进近最小跟驰距离的计算[J]. 航空计算技术, 2015(4): 46-48.NiuXialei,LüZongping,ZhangZhaoning.Minimumintraildistanceforpairedcloselyspacedparallel[J].AeronauticalComputingTechnique, 2015(4): 46-48.(inChinese)

[12] 张兆宁, 王丽丽, 顾平辉. 机场多跑道安全运行理论[M]. 北京: 科学出版社, 2014: 138-150.ZhangZhaoning,WangLili,GuPinghui.Thesafetyoperationmethodsofmultiplerunways[M].Beijing:SciencePress, 2014: 138-150.(inChinese)

(编辑：马文静)

Longitudinal Collision Risk Safety Assessment of Paired Approach to Closed Spaced Parallel Runways

Wang Jian, Zhang Zhaoning, Lu Fei

(National Key Laboratory of Air Traffic Operation Safety Technology, Civil Aviation University of China, Tianjin 300300, China)

In the busy airport capacity saturation phenomenon, closely spaced parallel runways implementing paired approach can effectively improve airport capacity, ease the airport runway congestion and flight delays and so on. For ensuring safety operation of paired approach, the safety distance calculation model of paired approach, based on the actual movement of paired approach on closely spaced parallel runways and the influence of navigation error and time of the two aircraft in the process of paired approach, is established. And the model is calculated by MATLAB software, and the risk variation curve of longitudinal collision with the relevant parameters is obtained. The results show that the collision risk of the pairing approach decreases with the increase of the starting distance of the two aircraft, and increases with the increase of the mean square error of the longitudinal positioning error of the aircraft, which verifies the correctness and rationality of the model.

paired approach; collision risk model; closed spaced parallel runways; navigation error

2017-02-19；

2017-04-11

国家自然科学基金(71701202)

王健,331269108@qq.com

1674-8190(2017)03-286-07

V355.1

A

10.16615/j.cnki.1674-8190.2017.03.006

王 健(1990-)，男，硕士，助理工程师。主要研究方向：空中交通规划与管理。

张兆宁(1964-)，男，博士，教授。主要研究方向：空中交通规划与管理。

卢 飞(1984-)，男，硕士，讲师。主要研究方向：空中交通规划与管理。

中央高校基本科研业务费(3122014D041)