T800碳纤维增强复合材料加筋壁板压缩稳定性试验及工程计算方法验证
2017-09-08吕毅张伟赵慧
吕毅,张伟,赵慧
(1.西安航空学院 飞行器学院,西安 710077)(2.西北工业大学 无人机特种技术重点实验室,西安 710065)
T800碳纤维增强复合材料加筋壁板压缩稳定性试验及工程计算方法验证
吕毅1,张伟2,赵慧1
(1.西安航空学院 飞行器学院,西安 710077)(2.西北工业大学 无人机特种技术重点实验室,西安 710065)
国内对T800碳纤维复合材料结构的研究刚刚起步,需要对其加筋壁板的稳定性进行系统地研究。通过改变蒙皮厚度、筋条间距、筋条几何参数等设计8种构型的试验件,进行压缩稳定性试验;考虑侧边边界条件及蒙皮有效宽度的影响,对两种常用的压缩屈曲载荷工程计算方法进行验证。结果表明:在相同筋条面积下,筋条惯性矩提高屈曲载荷增大,加筋壁板的破坏载荷主要取决于壁板的横截面积;蒙皮厚度和筋条间距对屈曲载荷的影响大于对破坏载荷的影响;对于薄蒙皮,当侧边简支且蒙皮有效宽度b=D-b2/2时,计算值与试验值最为接近;对于厚蒙皮,当侧边简支且蒙皮有效宽度b=D时,计算值与试验值最为接近。
T800碳纤维;复合材料;加筋壁板;屈曲;工程计算方法
0 引 言
作为飞机复合材料结构典型薄壁结构形式的加筋壁板结构在复合材料机翼和尾翼上已广泛应用[1-2]。复合材料加筋壁板结构的主要失效模式是丧失稳定性[3],即屈曲。为了保证结构的使用安全,对复合材料加筋壁板结构的稳定性进行分析是飞机复合材料薄壁结构强度校核的一个重要内容[4]。
对复合材料加筋壁板结构屈曲载荷和承载能力的计算,主要是工程计算方法和以特征值法、弧长法为基础的有限元分析方法[5]。工程计算方法,只需知道结构的几何参数和材料参数,就能快速地计算结构的屈曲载荷,其适用于飞机初步设计阶段,可快速给出整个结构的稳定性分析结论[6]。针对不同的结构工艺及材料体系的工程计算方法,国内外的学者进行了大量的研究,L.Boni等[7]和R.Vescovini等[8]对相关文献进行了总结;在国内,王菲菲等[9]、宋刚等[10]和葛东云等[11]进行了较为深入的研究。
由于T800碳纤维增强复合材料的强度和模量较T300、T700有很大的提升,分别提高约为50%和30%[12],使得T800碳纤维增强复合材料在商用大型飞机上得到了大规模的应用,例如T800H/3900-2预浸料被广泛应用于波音787飞机的机翼、机身和中央翼盒等主承力结构[13]。而国内对T800碳纤维增强复合材料结构的研究才刚刚起步[14],缺少针对相关结构设计的参考依据,例如试验数据、经过验证的计算方法等。因此,需要针对T800碳纤维增强复合材料加筋壁板结构的稳定性进行系统的研究。
本文针对T800碳纤维增强复合材料共固化工艺的加筋壁板,首先对试验件进行设计,通过改变蒙皮厚度、筋条间距、筋条几何参数等,共设计8个构型;然后,根据压缩稳定性试验的结果,分析蒙皮厚度、筋条间距、蒙皮与筋条刚度配比对试验件屈曲载荷和承载能力的影响;最后,对两种常用的压缩屈曲载荷的工程计算方法进行验证。
1 试验件设计
试验件的材料为T800级别的碳纤维预浸料,其材料属性如表1所示。

表1 T800碳纤维预浸料的材料属性
为了研究蒙皮厚度的影响,试验件的蒙皮包括薄蒙皮和厚蒙皮两种,其铺层信息如表2所示。

表2 薄蒙皮和厚蒙皮的铺层信息
为了研究蒙皮与筋条刚度配比的影响,在实际结构所采用Ⅰ型筋条的基础上,设计Ⅱ型和Ⅲ型筋条,其设计原则为:保持筋条横截面积不变,即筋条的重量不变,并保持筋条的铺层t1、t2和t3也不变,只改变筋条的尺寸,即改变筋条的腹板高度b3和下缘条长度b2,筋条的几何参数示意图如图1所示,三种筋条的铺层参数和尺寸参数分别如表3~表4所示。
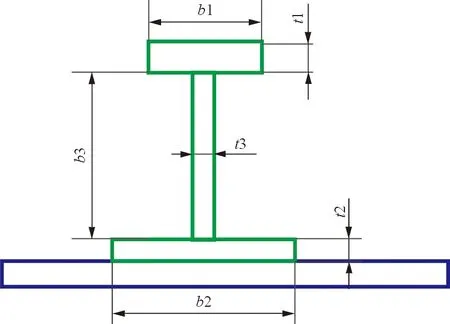
图1 筋条的几何参数示意图

铺层位置铺层比例/%铺层顺序厚度/mmt1(44.5/44.5/11)[45/0/0/-45/90/-45/0/0/45/45/0/0/-45/90/-45/0/0/45]3.384t2(44.5/44.5/11)[45/0/0/-45/90/-45/0/0/45]1.692t3(44.5/44.5/11)[45/0/0/-45/90/-45/0/0/45/45/0/0/-45/90/-45/0/0/45]3.384
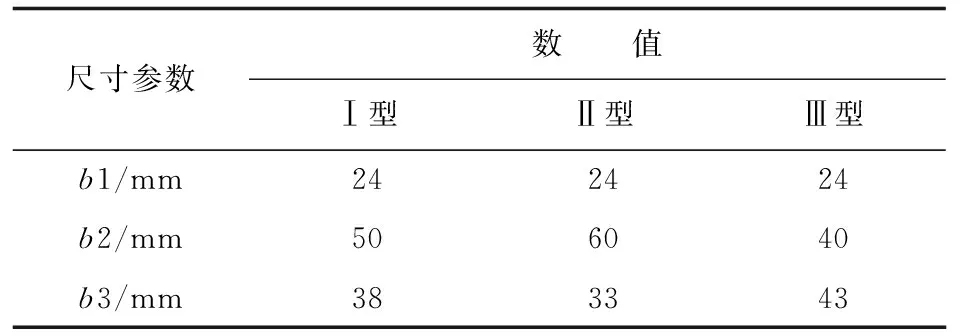
表4 三种筋条的尺寸参数
为了研究筋条疏密的影响,在实际结构所采用135 mm筋条间距的基础上,又增加110和165 mm两种筋条间距的试验件。
根据参考文献[15],当加筋桁条多于4根时,可以忽略壁板两侧边的边界支持条件的影响,故试验件采用5根筋条的结构。为了避免侧边的局部屈曲,需要将第1根和最后1根筋条都置于侧边上[16]。
压缩试验件共有8个构型,共25个试验件,1#构型试验件比其他构型试验件多1件,是为了进行全场莫尔云纹的观测,规划的试验件情况如表5所示。试验件示意图如图2所示。

表5 试验件列表

图2 试验件示意图
2 试验过程及结果分析
2.1 试验过程
试验之前,对试验件进行符合性检查,包括原始尺寸测量和超声C扫描。由于试验要加载到破坏,试验在500 T压缩试验机上完成。测量方案除了通常的应变片测量方案外,本文还采用屈曲云纹观测装置[17],实现试验件全场的莫尔云纹观测,与应变片测量方法相配合,可得到更为精确的屈曲载荷。
1#试验件破坏模式及云纹图如图3所示,其中1#-1和1#-4试验件在下端1/4处破坏;1#-2在中间位置破坏;1#-3试验件在蒙皮一侧未贴应变片而涂上了白色的哑光漆,以便进行全场莫尔云纹的观测,图3(c)为加载到850 kN时的云纹图。破坏时,1#-1试验件和1#-2试验件中1号、2号、3号、4号筋条与蒙皮分层;1#-4试验件中1号、3号、4号、5号筋条与蒙皮分层。

(a) 1#-1破坏模式

(b) 1#-2破坏模式

(c) 1#-3加载850KN时的云纹图

(d) 1#-4破坏模式
1#-1试验件筋条的载荷-应变曲线如图4所示,这里选取的5根筋条上的应变片的编号为25#~29#。可以看出:在试验件破坏之前,所有筋条的载荷-应变曲线线性都较好,筋条没有发生屈曲,即整个加筋壁板均未发生整体屈曲,其原因是由于采用的是T800级的新材料,所以设计较为保守,使得筋条的设计过强。1#-1试验件筋条上应变片的编号见图4(d)所示的试验件贴片方案。

(a) 1号、2号筋条载荷-应变曲线

(b) 3号、4号筋条载荷-应变曲线

(c) 5号筋条载荷-应变曲线

(d) 试验件贴片方案
2.2 试验结果分析
(1) 蒙皮与筋条刚度配比的影响
加筋板3种筋条的横截面积相同,差别在于腹板高度b3和下缘条长度b2的不同,腹板高度从低到高依次是Ⅱ型、Ⅰ型、Ⅲ型;下缘条长度从长到短依次为Ⅱ型、Ⅰ型、Ⅲ型。其中,1#、2#、3#试验件研究蒙皮厚度为2.256 mm时,筋条刚度的影响;4#、5#、6#试验件研究蒙皮厚度为3.760 mm时,筋条刚度的影响。
不同蒙皮和筋条的屈曲载荷及破坏载荷试验值如图5所示,可以看出:对于屈曲载荷,薄蒙皮时,Ⅱ型>Ⅰ型>Ⅲ型,厚蒙皮时也有着相同的趋势。

(a) 屈曲载荷

(b) 破坏载荷
Ⅰ型、Ⅱ型、Ⅲ型筋条对其形心轴的惯性矩如表6所示,其大小关系也为Ⅱ型>Ⅰ型>Ⅲ型。由此可知在保持筋条面积不变的情况下,筋条惯性矩提高,会使得屈曲载荷提高,与霍世慧等[18]得出的结论相同。

表6 三种筋条的惯性矩
对于破坏载荷,在相同蒙皮厚度下,Ⅰ型、Ⅱ型、Ⅲ型筋条的破坏载荷十分接近,表明加筋壁板的破坏载荷主要取决于壁板的横截面积,筋条刚度对其影响很小。
(2) 筋条疏密的影响
通过1#、7#、8#试验件研究筋条疏密对屈曲载荷和破坏载荷的影响如图6所示。

图6 不同筋条间距的屈曲载荷和破坏载荷试验值
从图6可以看出:筋条越密,屈曲载荷越大,破坏载荷也越大,承载能力更强。
根据试验件屈曲载荷与筋条间距的关系,可得出如下的经验公式:
(1)
本文将1#试验件的屈曲载荷定为Fcr0,筋条间距定为l0,分别将7#、8#试验件的间距代入式(1),可得其屈曲载荷,如表7所示,由经验公式计算的屈曲载荷与试验值吻合地非常好,7#的试验平均值与经验公式值的相对误差为1.3%,8#的试验平均值与经验公式值的相对误差为1.9%。

表7 经验公式计算的屈曲载荷值
(3) 蒙皮厚度的影响
通过1#与4#,2#与5#,3#与6#试验件研究蒙皮厚度对屈曲载荷和破坏载荷的影响。根据图7所示的结果,厚蒙皮与薄蒙皮的屈曲载荷、破坏载荷的比值如表8所示,考虑到5#试验件屈曲载荷试验值分散性较大,所以厚蒙皮与薄蒙皮的屈曲载荷比值应该在1.87左右,而破坏载荷的比值在1.36左右。
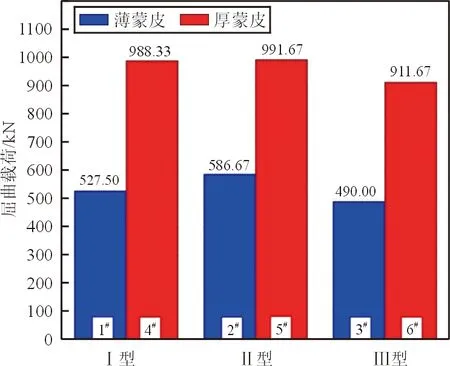
(a) 屈曲载荷
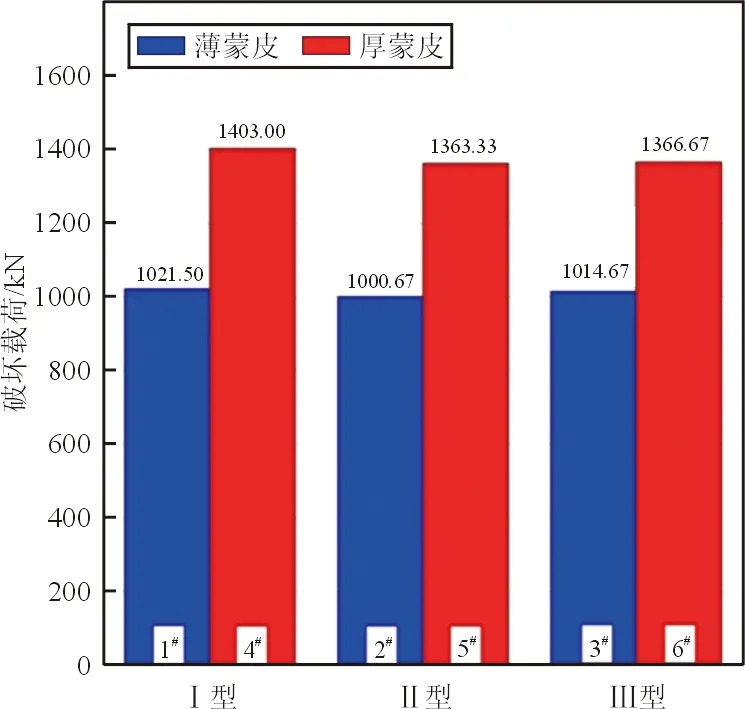
(b) 破坏载荷
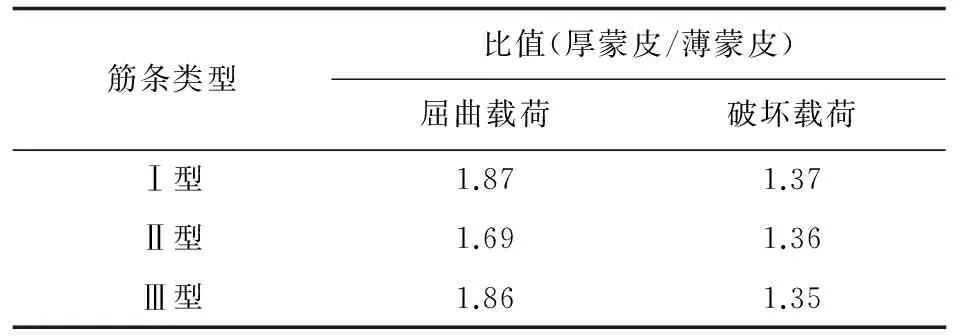
筋条类型比值(厚蒙皮/薄蒙皮)屈曲载荷破坏载荷Ⅰ型1.871.37Ⅱ型1.691.36Ⅲ型1.861.35
从表8可以看出:蒙皮厚度对屈曲载荷和破坏载荷的影响都比较大,而对屈曲载荷的影响要大于破坏载荷的影响。
3 工程算法的验证
对于压缩屈曲载荷的工程计算方法,常用的是参考文献[19](方法一)及ESDU-80023(方法二)所提供的方法,方法一和方法二的控制方程如下:
(2)
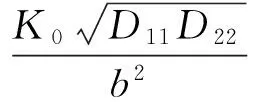
(3)
式中:Nxcr为压缩屈曲载荷,单位是N/mm;D11、D22、D12、D66为蒙皮的弯曲刚度系数,单位是N/mm;b为蒙皮的有效宽度,单位是mm;K可通过参考文献[19]的图2~图3查取;K0、C可通过ESDU-80023的图1查取。
本文对上述两种工程计算方法进行验证。
3.1 工程方法验证工况
对工程方法进行验证时,考虑侧边边界条件及蒙皮有效宽度b的影响:
(1) 试验中,两侧边的蒙皮看作是简支,但由于筋条刚度较大,筋条对蒙皮的影响,可以看作“简支”或“固支”两种边界条件,本文将分别进行讨论。
(2) 根据试验结果可知,如表3所示的筋条下缘条b2对屈曲载荷的影响显著,在进行屈曲载荷理论计算时,矩形层压板的宽度b值可分三种情况考虑:①不考虑缘条影响,即b=D,其中D为筋条间距;②减去下缘条的一半,即b=D-b2/2;③减去整个下缘条,即b=D-b2。
上述的两种情况相结合,共6种工况,如表9所示。

表9 工程计算方法验证的6种工况
3.2 工程计算方法结果
工程计算方法一和方法二的计算值与试验值的比较分别如表10~表11所示。
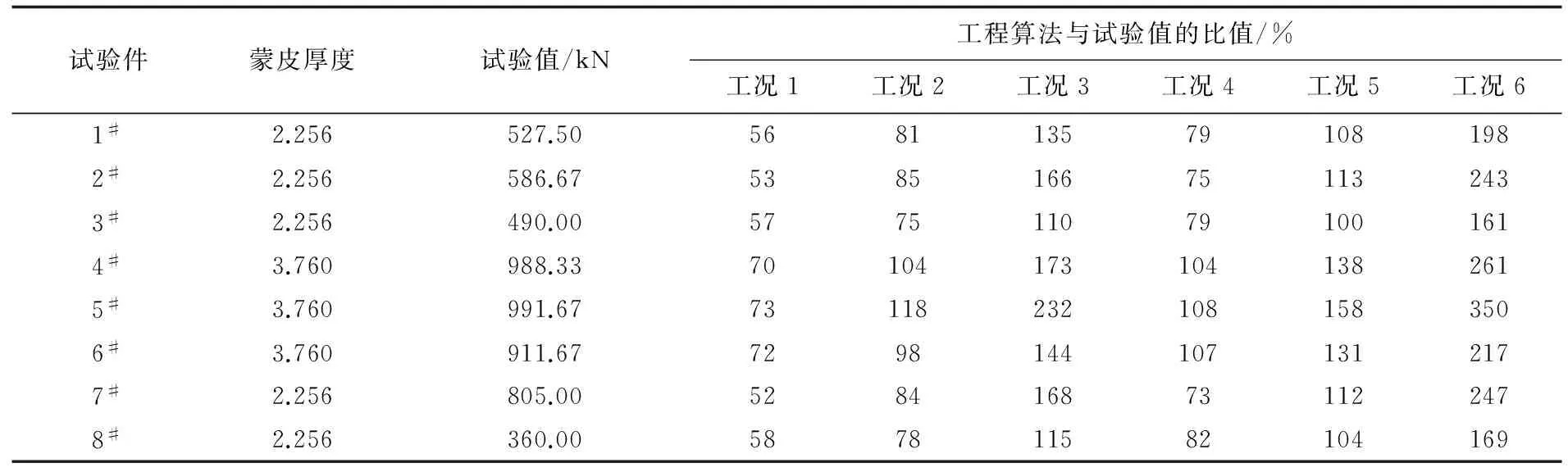
表10 工程计算方法一计算值与试验值的比较

表11 工程计算方法二计算值与试验值的比较
从表10~表11可以看出:工程计算方法一与工程计算方法二的计算结果十分接近,且方法一的计算值更精确。
对于薄蒙皮,采用方法一,以及工况2:侧边简支、宽度b=D-b2/2时,计算值相较于试验值是偏保守的,且最为接近的,工程计算值与试验值的比值在75%以上。这表明采用上述的工程计算方法已经具有了很好的精度,可以用在结构的详细设计中。
对于厚蒙皮,采用方法一,以及工况1:侧边简支、宽度b=D时,计算值相较于试验值是偏保守的,且最为接近的,工程计算值与试验值的比值在70%以上,由于对厚蒙皮的应变控制也很严苛,所以采用上述的工程计算方法是可以用在结构的详细设计中的。
4 结 论
(1) T800碳纤维增强复合材料压缩试验件的蒙皮首先发生局部屈曲,然后整个壁板破坏,从压缩试验件破坏模式可以看出,主要是筋条和蒙皮的压损破坏,在整个加载过程中,筋条不发生屈曲,筋条的设计较为保守。
(2) 在相同筋条面积下,筋条惯性矩提高,其屈曲载荷增大,而加筋壁板的破坏载荷主要取决于壁板的横截面积,筋条刚度对其影响很小;蒙皮厚度对屈曲载荷的影响大于对破坏载荷的影响;筋条间距对屈曲载荷的影响较大,对破坏载荷的影响较小,并根据试验数据得出了一个屈曲载荷与筋条间距的经验公式。
(3) 对于薄蒙皮,采用方法一,当侧边简支且宽度b=D-b2/2时,与试验值最为接近;对于厚蒙皮,采用方法一,当侧边简支且宽度b=D时,与试验值最为接近。
[1] 沈真, 柴亚南, 杨胜春, 等. 机翼结构用复合材料的力学性能要求[J]. 航空制造技术, 2010(1): 44-48. Shen zhen, Chai Yanan, Yang Shengchun, et al. Mechanical property requirements of composites systems for wing structures[J]. Aeronautical Manufacturing Technology, 2010(1): 44-48.(in Chinese)
[2] Fawcett A, Trostle J, Ward S. 777 Empennage certification approach[C]∥Proceeding of the 11th International Conference on Composite Materials (ICCM-11), July 14-18, 1997. Australia: 1-17.
[3] 杨乃宾, 章怡宁. 复合材料飞机结构设计[M]. 北京: 航空工业出版社, 2004: 1-10. Yang Naibin, Zhang Yining. Composite aircraft structure design[M]. Beijing: Aviation Industry Press, 2014: 1-10.(in Chinese)
[4] Barbero E J. Introduction to composite materials design[M]. Boca Raton, Florida: CRC Press, 2010.
[5] 李乐坤, 李曙林, 常飞, 等. 复合材料加筋壁板压缩屈曲与后屈曲分析[J]. 南京航空航天大学学报, 2016, 48(4): 563-568. Li Lekun, Li Shulin, Chang Fei, et al. Buckling and post-buckling of composite stiffened panel under compression[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(4): 563-568.(in Chinese)
[6] 王明春, 赵洁, 吴德锋, 等. 典型复合材料加筋壁板稳定性计算方法的比较研究及试验验证[J]. 飞机设计, 2016(3): 46-49. Wang Mingchun, Zhao Jie, Wu Defeng, et al. Comparative studies and experimental verification of stability calculation methods of typical composite stiffened panel[J]. Aircraft Design, 2016(3): 46-49.(in Chinese)
[7] Boni L, Fanteria D, Lanciotti A. Post-buckling behaviour of flat stiffened composite panels: experiments vs. analysis[J]. Composite Structures, 2012, 94(12): 3421-3433.
[8] Vescovini R, Bisagni C. Two-step procedure for fast post-buckling analysis of composite stiffened panels[J]. Computers & Structures, 2013, 128: 48-47.
[9] 王菲菲, 崔德刚, 熊强, 等. 复合材料加筋板后屈曲承载能力工程分析方法[J]. 北京航空航天大学学报, 2013, 39(4): 494-497. Wang Feifei, Cui Degang, Xiong Qiang, et al. Engineering analysis of post-buckling loading capability for composite stiffened panels[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 494-497.(in Chinese)
[10] 宋刚, 崔德刚, 董立君. 复合材料加筋板屈曲/后屈曲分析的应用[J]. 复合材料学报, 2017, 34(1): 96-103. Song Gang, Cui Degang, Dong Lijun. Application of buckling/post-buckling analysis for composite stiffened panels[J]. Acta Materiae Compositae Sinica, 2017, 34(1): 96-103.(in Chinese)
[11] 葛东云, 莫与明, 何柏灵, 等. 复合材料帽型加筋板轴压试验及承载能力预测[J]. 复合材料学报, 2016, 33(7): 1531-1539. Ge Dongyun, Mo Yuming, He Bailing, et al. Test and ultimate load capacity prediction of hat-stiffened composite panel under axial compression[J]. Acta Materiae Compositae Sinica, 2016, 33(7): 1531-1539.(in Chinese)
[12] 万爽. T800级碳纤维增强树脂基复合材料设计、分析及成型工艺方案研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. Wan Shuang. Grade T800 carbon fiber reinforced resin matrix composites design, analysis and forming process research[D]. Harbin: Harbin Institute of Technology, 2014.(in Chinese)
[13] 杨乃宾. 新一代大型客机复合材料结构[J]. 航空学报, 2008, 29(3): 596-604. Yang Naibin. Composite structures for new generation large commercial Jet[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(3): 596-604.(in Chinese)
[14] 何柏灵, 葛东云, 莫与明, 等. T800碳纤维增强复合材料双剪单钉连接的拉伸试验及强度估算[J]. 复合材料学报, 2016, 33(7): 1540-1552. He Bailing, Ge Dongyun, Mo Yuming, et al. Tensile tests and strength estimation for double-lap single-bolt joints in T800 carbon fiber reinforced composites[J]. Acta Materiae Compositae Sinica, 2016, 33(7): 1540-1552.(in Chinese)
[15] 中国航空研究院. 复合材料结构设计手册[M]. 北京: 航空工业出版社, 2004. Chinese Aeronautical Establishment Edited. Handbook of structural design of composites[M]. Beijing: Aviation Industry Press, 2004.(in Chinese)
[16] Luca Lanzi, etc. An experimental investigation on the post-buckling behavior of composite stiffened panels[J]. AIAA-2004-1566, 2004.
[17] 吕毅, 裴金利, 段继旺, 等. 屈曲云纹观测装置: 中国, 201220504321.1[P]. 2013-06-19. Lü Yi, Pei Jinli, Duan Jiwang, et al. Buckling moire observation device: China, 201220504321.1[P]. 2013-06-19.(in Chinese)
[18] 霍世慧, 王富生, 王佩艳, 等. 复合材料机翼加筋壁板稳定性分析[J]. 应用力学学报, 2010, 27(2): 423-427. Huo Shihui, Wang Fusheng, Wang Peiyan, et al. Stability analysis on the ribbed panel of the composite wing[J]. Chinese Journal of Applied Mechanics, 2010, 27(2): 423-427.(in Chinese)
[19] 中国航空研究院. 复合材料结构稳定性分析指南[M]. 北京: 航空工业出版社, 2002. Chinese Aeronautical Establishment Edited. Guide for structural stability analysis of composite materials[M]. Beijing: Aviation Industry Press, 2002.(in Chinese)
(编辑:赵毓梅)
Compression Stability Test and Engineering Calculation Methods Verification ofT800 Carbon Fiber Reinforced Composite Stiffened Panels
Lü Yi1, Zhang Wei2, Zhao Hui1
(1.School of Aerocraft Engineering, Xi’an Aeronautical University, Xi’an 710077, China)(2.Laboratory of Science and Technology on UAV, Northwestern Polytechnical University, Xi’an 710065, China)
The research on the structure of T800 carbon fiber composite has just started in our country, so it is necessary to make a systematic study on the stability of stiffened panel with T800 carbon fiber reinforced composite. The test articles of 8 configurations are designed by varying the skin thickness, stiffener spacing, stiffener geometric parameters, and the compression stability tests are carried out. Considering the influence of the lateral boundary condition and the effective width of skin, two commonly used compression buckling load engineering calculation methods are verified. Results show that when the moment of inertia increases the buckling load will increase in the same stiffener area, the failure load of stiffened panels mainly depends on the cross sectional area of the panels, and the effect of skin thickness and stiffener spacing on buckling load is greater than that on failure load; For the thin skin, when the lateral simply supported and the effective width of skin isb=D-b2/2, the calculated value is closest to the experimental value; For the thick skin, when the lateral simply supported and the effective width of skin isb=D, the calculated value is closest to the experimental value.
T800 carbon fibers; composite; stiffened panel; buckling; engineering calculation method
2017-06-14;
2017-07-05
陕西省自然科学基金(2016JQ1043)
吕毅,lvyi112@aliyun.com
1674-8190(2017)03-268-09
V
A
10.16615/j.cnki.1674-8190.2017.03.004
吕 毅(1981-),男,博士,高级工程师。主要研究方向:复合材料力学行为的表征。
张 伟(1981-),男,硕士,工程师。主要研究方向:飞机结构环境适应性评估。
赵 慧(1992-),男,硕士,助教。主要研究方向:飞行器结构的强度分析。
陕西省教育厅科研计划项目(16JK1396)
西安航空学院校级科研基金(2016KY1101)
