基于多传感器融合的抽油机运动周期的研究
2017-09-07仲志丹马利丹
仲志丹 马利丹

摘 要: 对油井示功图的分析是评定深井泵、抽油机与抽油杆工作状态的重要手段。抽油机运动周期作为示功图的重要参数,其准确性直接影响示功图的精度。针对采用单一悬点加速度的方法确定的抽油机运动周期误差较大等缺点,提出一种多传感器融合的抽油机运动周期的计算方法。首先对不同传感器采集的同周期的悬点加速度、悬点载荷、电动机电功率3种信号进行卡尔曼滤波,消除干扰噪声;其次对滤波后的信号分别从时域和频域计算出周期值;最后对3种信号周期值进行加权融合,确定最优周期值。实验表明:多传感器融合的方法比单一加速度法所确定的抽油机运动周期具有更高的准确度。
关键词: 抽油机; 卡尔曼滤波; 多传感器; 频域FFT
中图分类号: TN601?34; TN919.5 文献标识码: A 文章编号: 1004?373X(2017)16?0022?04
Abstract: Analysis on dynamometer card of well is an important means to assess the operating status of the deep well pump, pumping unit and sucker rod. The motion period of pumping unit is taken as an important parameter of the dynamometer card, whose veracity affects the accuracy of dynamometer card directly. A method to calculate the motion period of pumping unit based on multi?sensor fusion is proposed to overcome the poor exactitude disadvantage of the method which adopts single suspension point accelerated speed to determine the motion period of pumping unit. Three kinds of signals (suspension point acceleration, suspension point load and motor electric power) collected by different sensors in same period are filtered by Kalman filtering method to eliminate interference noise. The period values of the filtered signals are calculated in the time domain and frequency domain respectively. The optimal period values are obtained by the weighted fusion method. The experimental results show that the multi?sensor fusion method has higher veracity of the motion period value of the pumping unit than that obtained by the single acceleration method.
Keywords: pumping unit; Kalman filtering; multi?sensor fusion; frequency domain FFT
0 引 言
示功仪是油田生产维护用的一种常用仪表,它通过检测抽油杆周期性上下运动时不同位移处抽油杆所承受的载荷来反映油井的工作状况。传统的拉线法测位移方法原理简单,精度较高,但仪器笨重、断头率高、局部磨损严重、寿命短等不足,不适合工业现场安装布局[1]。倾角传感器测位移的方法,因与载荷传感器安装位置不同在实际中多有不便;间接测量功图的方法:利用电参量,电流、功率、扭矩等反推出载荷、位移关系在实际应用中还不成熟[2]。目前示功仪中最常用测位移的方法是通过对悬点加速度二次积分求得。但微小的周期偏差都会在积分中被放大,使算出的位移有较大误差,甚至会导致载荷、位移曲线无法闭合,对仪器精度影响很大。所以依靠单一加速度确定抽油机运动周期的方法存在一定弊端。
在油井抽油机工作过程中,悬点加速度、载荷、电动机功率及扭矩等信号都是随着抽油机负载的变化周期性变化的,并且周期一致。綜上所述,本文提出融合更多可测信号:加速度、载荷、功率的方法,分别计算出各自周期,再对各个信号的周期进行融合,从而得出准确的抽油机运动周期。
1 理论分析
1.1 单一加速度估算周期对二次积分后位移的影响
实际工程测量得到的加速度信号中包含各种干扰因素引起的直流误差项及外界噪声,测得的加速度信号可表示为:
[a(t)=f(t)+n(t)+g0] (1)
式中:[f(t)]为真实加速度;[n(t)]为外界噪声;[g0]为直流分量。因此必须对加速度信号进行滤波消噪。设[a′(t)]为滤波处理后加速度信号,对其一次定积分得到速度值:
[vT1=0T1a′(t)dt+v0] (2)
由速度积分得到位移值:
[sT1=0T1v(t)dt+s0] (3)
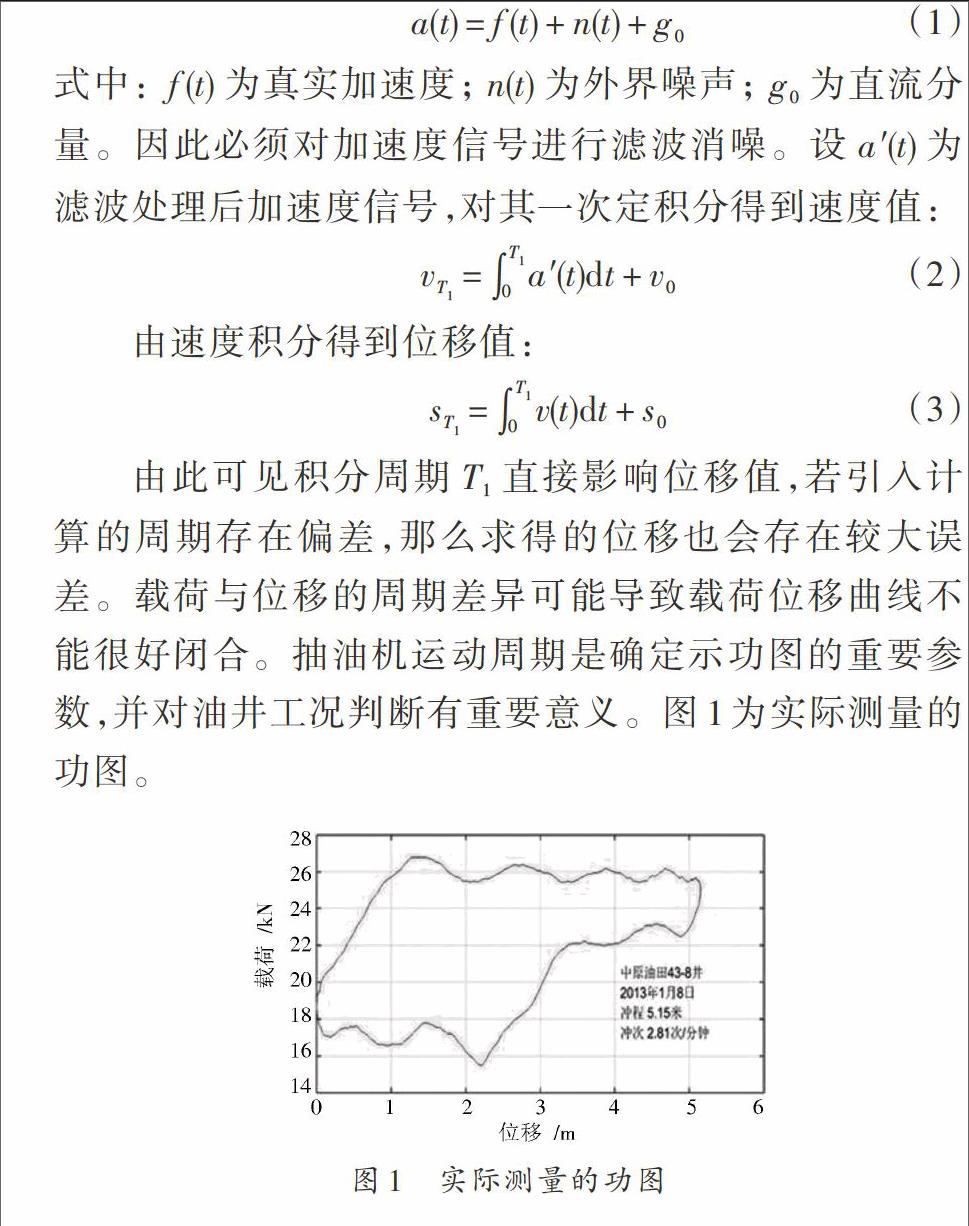
由此可见积分周期[T1]直接影响位移值,若引入计算的周期存在偏差,那么求得的位移也会存在较大误差。载荷与位移的周期差异可能导致载荷位移曲线不能很好闭合。抽油机运动周期是确定示功图的重要参数,并对油井工况判断有重要意义。图1为实际测量的功图。endprint
1.2 整体设计
抽油机在运动过程中存在的各种机械振动,加上传感器本身的一些漂移,采集到的数字信号中必定混有噪声和奇异点,选择合适的滤波算法必不可少。在抽油过程中,悬点加速度、载荷及电动机功率都是随着抽油机负载的变化周期性变化的,并且普通示功仪中都有精度不同的多个加速度传感器和一个载荷传感器。虽然没有相应的电参量传感器,但实时电功率信号却较易得到。为了算出更加准确的抽油机运动周期,本文提出融合加速度信号,载荷信号,电功率信号的方法计算出抽油机周期,具体结构如图2所示。
1.3 卡尔曼滤波算法
卡尔曼滤波是一种迭代算法,最小均方误差估计是其最佳准则,其基本算法思想为在最佳估计的准则下,以信号与噪音状态空间为模型,用上次的估计值与本次的测量值,对状态变量估计进行更新,求出本次的估计值,建立离散的过程系统和测量方程对待处理的数据进行满足最佳准则的估计。
卡尔曼滤波器不断运行直到系统过程结束,还要更新k状态下协方差:
[P(k)=(I-Kg(k)H)P(kk-1)] (10)
式中,矩阵I为单位矩阵。当系统进入[k+1]状态时,[P(k)]就等于[P(k-1)],以自回归的方式运算下去。
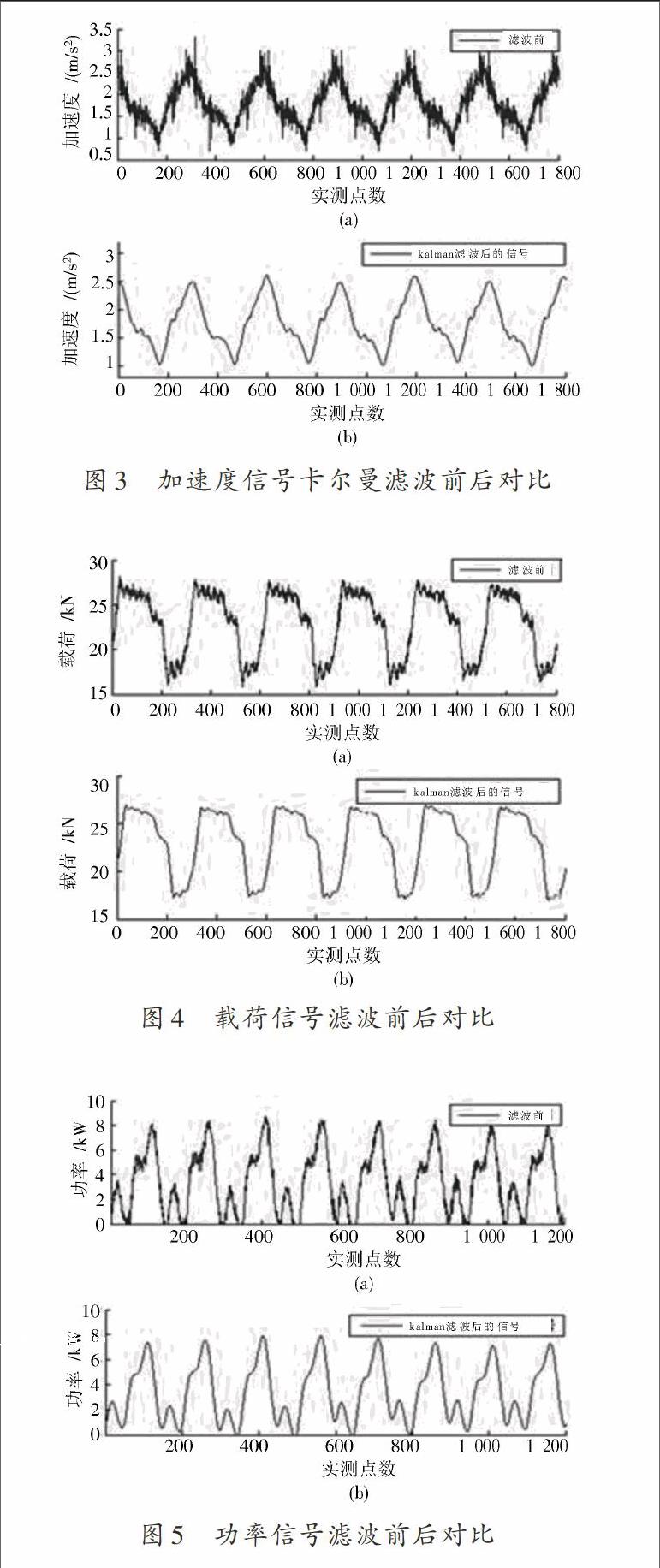
综上所述,由初始状态[X0],初始误差[P0],当前观测值[Z(k)],Q和R取经验值,便能求得当前最优估计[X(k)]和误差值[P(k)]。图3~图5为对实测加速度、载荷、电动机功率3种信号的滤波效果。
由卡尔曼滤波后的信号消除了大幅度的脉冲干扰,同时使图像轮廓平滑清晰。
2 运动周期分析
2.1 时域周期计算
在抽油机上下运动的过程中,如图6所示,加速度maxi组就是相对位移的零点,而mini组为相对位移的最大点,两个接近的区域最大值点或最小值点便是一个周期。把极值点进行归并,找出极值坐标,结合已知的不同信号采样频率就可以算出加速度的周期,同样可以求出载荷与功率信号的周期。
2.2 频域周期计算
将信号从时域转换成频域,可以从频谱中分析出其周期,但由于FFT运算存在量化误差,当输入信号的频率不在FFT量化频率点处时,直接用FFT运算的最大谱线位置来估计信号的频率,将存在量化误差。文献[3]给出的频率估计算法,在对输入信号进行一次FFT运算后,利用最大谱线及其相邻的一根次大谱线进行插值来确定真实频率位置,即Rife算法。当信号的真实频率处于两相邻量化频率之间的中心区域时,Rife算法精度很高;但是在FFT量化频率附近的误差却较大。MRife算法[4]通过对输入信号进行频谱搬移,使得信号的频率始终位于两相邻量化频率之间的中心区域,提高了频率估计精度。
(4) 若重新计算A∈[0,[13]],则将r取反,返回步骤(3)。
MRife算法通过对原始信号的平移,保证频率中心区域精度高的优势,使得频率估计精度大为改善。
3 实验验证
3.1 周期比对
为了验证算法的可靠性,用Matlab对同周期的加速度、载荷、功率信号进行处理。从图3~图5可以看出卡尔曼滤波既抑制信号中的脉冲干扰,又能滤除随机噪声。滤波后的信号曲线变得平滑,通過极值坐标就能计算其周期。对滤波后的3组信号分别进行FFT, 可得加速度、载荷、功率信号最大谱线和次大谱线的幅值,利用上文频域估计的方法可以算出3种信号周期。
表1为对同步测得的10组数据[ai,Fi,Pi]中前3组的周期计算结果,其中周期真值为15 s。ai代表加速度,Fi代表载荷,Pi代表电功率。
表1 不同信号周期值
10组优选结果表明,对于加速度信号和载荷信号频域估计周期更为准确,电功率信号利用时域计算出的周期更加接近真实值。因此加速度周期和载荷周期取频域计算所得值[Ta],[TF],功率周期取时域计算所得值[TP]。
3.2 权值确定
由贝塞尔公式可得单次测量标准差计算公式:
[σ=i=1nvi2n-1] (15)
式中,[vi]为残差。n次等精度测量中,算术平均值的标准差为:
[σx=σn] (16)
对于同一种信号多次测量,认为是等精度测量。由式(16)可计算出3种信号算术平均值的标准差[σxa],[σxF],[σxP]。
在不等精度测量中,单位权化的实质是使任何一个量值乘以自身权数的平方根,得到新的量值权数为1,每组测量结果的权值与其相应的标准差平方成反比[5],本文中3种信号有相同的理论周期值,但信号自身不同,为不等精度测量,所以3种信号权值比为:
[pa:pF:pP=1σ2xa:1σ2xF:1σ2xP] (17)
又权值和为1,由式(17)可以算出3种信号的权值[pa,pF,pP]。
因此根据权值确定抽油机运动周期的计算公式为:
[T=paTa+pFTF+pPTP] (18)
对10组数据按上述公式进行计算处理,并与单一加速度确定的周期相对比,如图7所示。
由图7可以看出融合后的10组周期值更加接近理论值。
由表2可以看出多信号融合后的周期值比单一加速度确定的周期值有更高的精度。
表2 融合后周期值与单一加速度最大相对误差
4 结 论
本文提出了一种多传感器信号融合计算抽油机运动周期的方法。利用卡尔曼滤波有效地滤除原始信号中的噪声,对滤波后的加速度、载荷、功率分别利用时域峰值坐标法和频率估计法计算周期并进行对比取优。最后对3种信号周期进行加权融合,实验结果表明,多传感器融合的周期计算方法提高了周期的计算精度。
参考文献
[1] 于云华,张家珍,时海涛,等.基于加速度传感器的油井示功图位移测量技术研究[J].电子产品世界,2009(9):25?27.
[2] 檀朝东,罗小明,赵海涛,等.抽油机井示功图间接测量方法评价研究[J].中国石油和化工,2008(14):49?51.
[3] 张庆国.基于FFT并实时修正的Rife频率估计算法[J].信号处理,2009(6):1002?1004.
[4] 谢胜,陈航,于平.基于FFT并二次修正的Rife频率估计算法[J].探测与控制学报,2010(4):48?53.
[5] 费业泰.误差理论与数据处理[M].北京:机械工业出版社,2004.
[6] 焦竹青,熊伟丽,张林,等.基于接近度的多个传感器数据融合方法研究[J].压电与声光,2009(5):771?774.
[7] 容太平,沈承虎,袁中平,等.用加速度传感器测量位移的原理与误差分析[J].华中理工大学学报,2000(5):58?60.
[8] 凯.统计信号处理基础:估计与检测理论[M].北京:电子工业出版社,2006.
[9] 初昀,常敏,王戈.基于油田示功仪的加速度信号处理方法[J].数据通信,2014(1):43?46.
[10] 时世晨,单佩韦.基于EEMD的信号处理方法分析和实现[J].现代电子技术,2011,34(1):88?90.
[11] 郭敏,尹光洪,田曦,等.基于三轴加速度计的倾斜角传感器的研究与设计[J].现代电子技术,2010,33(8):173?177.endprint
