农村初中数学智慧课堂的建构与实践

孙大庆

[摘 要] 本文从农村初中生的特点出发，探讨了数学智慧课堂的建构与实践，指出自主性与针对性是建构智慧课堂的基石，有效性与多样性是建构智慧课堂的策略，灵活性与发散性是建构智慧课堂的灵魂.

[关键词] 农村初中；数学教学；智慧课堂；建构实践

我们的数学教学不仅要考虑数学内容的自身特点，还要积极研究学生的心理规律，要善于从学生的生活经验出发. 在农村初中从教多年，笔者深深感受到农村初中的学生大多有知识面狭窄、学习能力弱等特点，特别是留守儿童，父母长期在外打工，家庭教育严重缺失. 这样的学生更需要教师充分运用教学艺术来建构智慧课堂. 课堂上，教师要以学生的智慧发展为核心，让数学教学更具有生命力和创造性，由此才能对学生的心智起到启迪作用，才能让学生在充分的师生互动中感受到学习的快乐.

自主性与针对性是建构智慧课堂的基石

智慧课堂需要教师结合具体的教学内容，充分联系学生的认知水平编制合适的导学案，由此激活学生尝试的勇气. 学生敢于尝试才能促成创新与成功. 在一般的数学课堂上，对于新授知识，学生都有“三分生、七分熟”的基础，只要教师善加引导，学生完全可以通过自己的尝试来获取新知. 导学案将为学生提供尝试的基础，这也有助于学生潜能的发掘，从而帮助学生获得巨大的成功. 当然，教师还要在课前整合学生在导学案中所暴露出的问题，并由此调整教学设计，进而彰显课堂的自主性与针对性，这些也正是智慧课堂的建构基石.

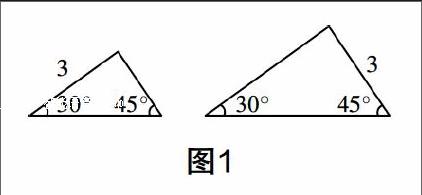
例如教学“全等三角形的判定（2）”一课时，教师先通过导学案指导学生进行画图、实验和探究，学生能自主形成结论：两角及其夹边对应相等的三角形全等（即ASA）. 学生继续探索：如果两个三角形两角及其一角的对边对应相等，那么它们是否存在全等关系呢？为什么？学生有的结合导学案中推导ASA的图形，找出边角相等的关系，得出结论——全等，原因即为ASA；也有学生画出如图1所示的图形，得出结论——不全等. 从上述情形可以发现：学生结论存在分歧的原因在于他们对“AAS”表述中“对应”一词的理解不一定清楚. 为此，教师可以预先让学生用剪刀剪出两个全等三角形，让学生通过纸质模型来理解“对应”的含义.

在上述案例中，学生通过合作交流明确了错误的原因，并由此澄清了有关“对应”一词的理解. 在全等三角形判定定理的教学过程中，很多学生只会盲目地记“ASA”“SAS”“AAS”等符号，完全忽略了判定定理的本质，而在教学中，如果和学生以咬文嚼字的方式来探索“对应”一词的概念，显然又太过机械，这不是我们期望中的智慧课堂. 而现在我们通过学生导学案的完成发掘他们的错误，进而引导学生通过自主探究和合作交流来实现这一词语的认识，由此则能实现针对性纠正.

教师研究学生自主学习所暴露的问题，从“以学定教”的理念出发，针对性地调整教学策略，引导学生进行更深层次的探索，这能提升教学效率.

有效性与多样性是建构智慧課堂的策略

智慧课堂的构建不能机械而僵化，笔者也很反对动辄就以某种模式或框架来架设课堂结构，这是新课程理念的机械化解读. 智慧课堂应该富有生命活力，即教师要能够根据具体的内容特点和学生的课堂反应来创设多样化的课堂情境，由此更加有效地帮助学生发现数学规律.

例如，引导学生对三角形中位线定理进行探索时，如果按照教材上的思路来组织教学，那只能为学生呈现抽象的推理过程和枯燥的数学结论. 为了避免出现上述状况，教师可以在上课之前让每一个学生自己裁剪一张形状任意的三角形. 课堂上，教师安排学生自主思考并动手操作，将一个三角形分成两部分，并尝试着将它们拼成一个平行四边形. 教师提供充足的时间让学生展开思考和探索，鼓励学生将自己的想法付诸实践，还安排学生到实物投影仪上将自己裁剪和拼凑的过程展示出来.

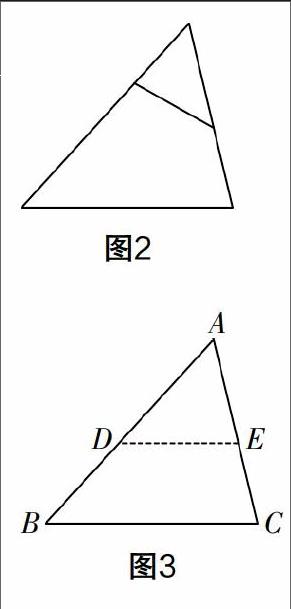
一个学生就是按照如图2所示的方式进行裁剪，却没有拼成预想中的图形，这时教师鼓励学生继续思考. 这个学生经历了错误之后，思维更加冷静：要想能最终拼成一个平行四边形，就要让新出现的小三角形和剩下来的四边形两条边相等（如图3，有AD=DB且AE=EC）.

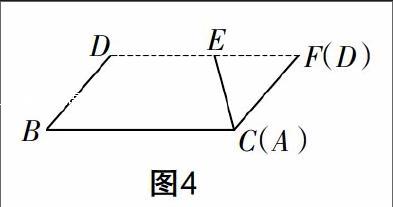
这样，学生通过对折让A，B两点重合，得到这条边的中点D，又通过类似的操作得到AC边的中点E，然后学生沿着线段DE将△ABC剪开，并把△ADE围绕E点旋转半周，拼成如图4所示的四边形BCFD. 由于D，E，F三点在同一直线上，且CF和BD两条边平行且等长，因此可以证得上述四边形为平行四边形.

要让学生能够产生学习兴趣和热情，教师在建构智慧课堂时应采用相应的教学策略，创设兼具有效性与多样性的情境. 在初中数学课堂上，教师可组织学生进行各类游戏、实验、比赛，还可以通过数学故事、数学谜语等形式实现情境的创设，这样的处理不仅可以开展丰富的教学活动，还能促成数学知识的高效传播.

灵活性与发散性是建构智慧课堂的灵魂

智慧课堂的本质是要充分激活学生的思维，让学生能以充满智慧的姿态进行学习，这也必将促进学生多元智能的发展. 为此，教师要注意课堂的灵活性与发散性，即教师要通过各类生动而有趣的教学活动，将学生的思维和想象引向更加广阔的空间，也只有在这样的数学课堂上，学生思维的灵活性和发散性才能得到充分发展. 灵活性是创新思维的基础，发散性是创新思维的核心，这两种性质将从根本上冲破思维定式的桎梏，引导学生从多个方面、多个角度对问题进行猜想、拓展和延伸，这也将帮助学生领会数学思维的多变性与开放性.

例如，指导学生对“相交线与平行线”进行复习时，教师可以给出以下例题：如图5，已知∠A+∠C=∠AEC，请判断直线AB与CD是否存在平行关系，并阐述理由. 作为复习课，学生已经具备一定的知识基础，如果只是让学生做题和讲解，很多学生未必有参与热情，特别是那些基础较好的学生，他们很难全身心地投入课堂. 为此，教师要采用更加灵活的方法来指导学生拓宽探索思路：教师预先准备两个细木条（作为待证明的两条边AB和CD）、一根橡皮筋、图钉，然后教师将橡皮筋固定在A，C两点之间，并用图钉拉着橡皮筋将其钉到E点.

如何进行判断和证明呢？学生都知道这样的问题需要添加辅助线，那么如何添加呢？部分学生刚开始时都不知道如何操作，教师可以通过移动图钉的方式来启发学生：将E点移动到线段AB上、CD上以及AC上，指导学生构建由特殊到一般的思路，最终实现问题的解决. 学生对操作进行观察与思考，发现这两条平行线好像缺少一条截线，又貌似缺少一条平行线. 这时，教师要鼓励学生进行积极地尝试和检验. 最终，在彼此交流中，学生一共发现了六种不同的处理方法，他们的思路被彻底打开，整个课堂完全沉浸在热烈的讨论与思考之中. 这时，教师再进一步将课堂交给学生，让他们自己到讲台上挪动图钉位置，并构成如图6所示的若干个新图形. 在此基础上，学生再进一步地探索让新图形中AB与CD两条线实现平行的条件，整个课堂更加热闹，学生的参与热情也更加高涨.

教师此时再顺势将题目进行拓展：如图7，∠1，∠2，∠3，∠4这四个角满足什么关系时，可以让直线AB与CD平行？学生趁热打铁，用刚刚获得的思路展开分析，很快便实现了问题的解决.

在上述案例中，原本只是一个较为平实的封闭式问题，通过教师灵活的引导，就演变成一个开放性问题，这样的处理，既能暴露学生的思维过程，还能促进学生举一反三、触类旁通，让他们思维的发散性和灵活性得到充分发展.

智慧课堂是初中数学教学中的鲜花与阳光，它能指导学生以更加积极的姿态来发现问题，并开启思维活动. 通过上述方法，我们可以更有效地调动学生的学习热情，进而主动地参与到探究过程中，此外，我们还将培养学生敢于探索、勇于创新的精神，让学生的各项活动闪烁出智慧的光芒.