通用飞机富勒襟翼多目标优化

魏 闯, 张铁军, 刘铁中(. 中国航空工业空气动力研究院 高速高雷诺数重点实验室, 辽宁 沈阳 0034； . 中国航空工业空气动力研究院 低速高雷诺数重点实验室, 黑龙江 哈尔滨 5000)

通用飞机富勒襟翼多目标优化

魏 闯1,*, 张铁军1, 刘铁中2
(1. 中国航空工业空气动力研究院 高速高雷诺数重点实验室, 辽宁 沈阳 110034； 2. 中国航空工业空气动力研究院 低速高雷诺数重点实验室, 黑龙江 哈尔滨 150001)

针对通用飞机高效增升装置设计的需求，提出了同时优化富勒襟翼缝道宽度、搭接量、襟翼偏角和襟翼外形的多目标优化设计方法。建立了基于椭圆方程的富勒襟翼参数化方法和RBF网格变形方法，优化算法采用快速非支配排序遗传算法(NSGA Ⅱ)，以求解雷诺平均N-S方程为气动评估方法并采用集群分布并行计算以缩短优化时间。以GA(W)-1为基准翼型，以增加线性段(6°)和接近失速迎角(13°)升力系数为目标进行富勒襟翼优化，16计算节点下耗时约8 h，获得最终Pareto前沿面，并对优化变量进行了相关性分析，相比初始构型，Pareto前沿面构型最大使迎角6°和13°升力系数增加7.03%和3.42%，说明该优化方法快速有效的。

富勒襟翼；多目标优化；NSGA Ⅱ；N-S方程；Pareto前沿面

0 引 言

起飞和着陆状态的增升装置设计，是飞机设计中的一个重要环节，是提高起飞重量，缩短起降滑跑距离，增强机场适应性的关键技术[1]。目前增升装置研究主要针对大中型运输机进行[1-3]，通用飞机的尺寸和起降速度较大中型运输机小很多[4]，飞行雷诺数约低一个量级，大多为数百万，由于缝道参数对雷诺数敏感，使得其襟翼缝道内流动与翼面分离特性有较大的变化，更易产生流动分离。而且通用飞机增升装置系统不能过于复杂，如何在保证通用飞机增升装置的设计要求下满足气动增升效率是通用飞机增升装置设计的关键技术之一。增升装置通常采用多段翼型形式，多段翼型气动性能好坏直接影响其气动性能，单缝富勒襟翼以其构型相对简单、增升效率高为通用飞机较多采用的一种增升装置形式。

缝道参数对多段翼型气动性能的影响是主要的，近些年来，国内外研究者竞相开展缝道参数优化设计[5-11]研究，取得很大成果，建立了一些缝道参数优化设计方法。Sangho Kim等[5]利用黏性伴随方法通过求解N-S方程对30P30N三段翼型进行了优化，提高翼型升力性能。Ernesto Benini等[6]使用多目标遗传算法对三段翼型的起飞和着陆状态的气动特性进行优化，但是优化过程中采用MSES软件进行气动评估很难获得大迎角计算结果，优化过程中并未对大迎角气动性能进行优化，而最大升力系数是增升装置的一个重要技术指标。白俊强等[10]分别对Bezier和B样条曲线参数化方法进行研究，建立了满足几何约束的多段翼型的参数化方法，利用改进粒子群优化算法和RBF动网格方法进行多段翼型优化。倪昂修等[11]对NSGA Ⅱ算法进行改进，对多段翼型缝道参数进行优化设计，以18°迎角升力系数最大为优化目标获得了较为满意的结果。

本文针对通用飞机富勒襟翼设计的需求，利用数值模拟方法研究了富勒襟翼缝道宽度、搭接量、襟翼偏角以及外形对其气动性能的影响，提出了同时优化富勒襟翼缝道宽度、搭接量、襟翼偏角和襟翼外形的多目标优化设计方法，并开展二维富勒襟翼优化设计。

1 富勒襟翼参数化和计算方法

1.1 富勒襟翼参数化方法

如图1所示，把襟翼外形分成5段，通过如下椭圆方程控制各段外形生成[12]。

每个翼段利用两点的坐标和其中一点处的斜率可得到求解系数a、b、c的联合方程组。保证相邻两段交点处斜率相同保证襟翼外形光顺，襟翼外形控制参数和含义见表1，实现过程为：

1) 由C_F和FRY2求得点2相对基本翼型位置，将坐标原点设置在点2位置，则点2自动满足斜率为无穷大；

2) 襟翼点1处后缘与基准翼型外形相同且在点1处相切，由FRX1即可确定点1坐标和点1处斜率S1，点3坐标由FX3和FRY3确定，从而求得1～2段外形方程；

3) 给定C_M以及ΔY(ΔY1和ΔY2之和)值确定点5坐标；5-6的弦向长度一般取2%翼型弦长，同时保证5～6段在点6处与与基本翼型相切即可得到点6坐标和点6处斜率S6，从而确定5-6段外形，同时求得点5处斜率S5。

4) 由FX4和FRY4确定点4坐标，与(3)确定的点5坐标和S5即可确定4～5外形，同时求得点4处斜率。3～4段外形也由同样的方法确定。

5) 最后，由点1、3坐标，点3处斜率确定2～3段外形。

该方法生成外形曲线光滑，而且很容易实现控制多段翼型主翼弦长、襟翼弦长以及襟翼厚度，能够满足工程需要。缝道宽度Gap、搭接量O/L和襟翼偏角δf定义见文献[12]。

图1 富勒襟翼参数化Fig.1 Fowler flap parameterization

参数名含义C＿M固定翼长度，用来确定点5横坐标C＿F襟翼弦长FRX1点1到点2横向距离与点2处翼型厚度比值FRY2点2到基本翼型下翼面距离与当地翼型厚度比值FX3点3横坐标FRY3点3到基本翼型下翼面距离与当地翼型厚度比值FX4点4横坐标FRY4点4到基本翼型下翼面距离与当地翼型厚度比值ΔY1主翼后缘厚度ΔY2主翼下翼面后缘到襟翼的垂直距离注：坐标原点在点2处。

1.2 网格生成和径向基函数网格变形方法

计算网格为结构网格，C-H型网格拓扑结构，计算域入口端距翼型前缘15c，出口端距离后缘24c，上下边距翼型各为15c，在流场参数梯度较大的区域如缝道处、主襟翼尾迹区以及附面层区域充分加密，第一层网格高度为翼型弦长的1.0×10-5倍，保证过渡和正交性，共5.1万网格节点。

式中:F(r)是插值函数；N代表网格节点数目；φ(‖r-ri‖)是径向基函数的一般形式，‖r-ri‖是矢量r到ri的距离，r为网格节点的坐标，ri代表径向基函基点的坐标；ϖi是径向基函数相对应的权重系数。本文径向基函数采用计算效率与网格变形的质量都较好的Wendland’s C2函数[13-14]。

图2给出襟翼附近初始和变形后网格，可以看出，RBF网格变形方法的鲁棒性较高，对于缝道宽度、搭接量、襟翼偏角以及襟翼外形大幅度变化都能获得较好的变形网格，保证了优化过程中CFD结果的可信度。

(a) Initial grid

(b) Deformed grid

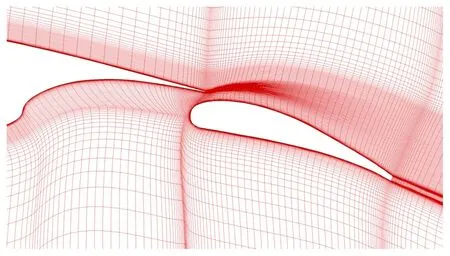
(c) Deformed grid(Gap=0.014、O/L=0.02、δf=20°、FRY2=0.2)

图2 富勒襟翼网格变形结果
Fig.2 Grid deformation of Fowler flap configuration

1.3 数值求解方法及验证

多段翼型缝道中的流动很复杂，几乎完全是由黏性绕流决定的，如何对其进行精确的计算一直是研究的重点。本文通过求解RANS方程进行富勒襟翼气动力计算，湍流模型选用能够较为准确的模拟分离流、旋涡流等复杂流动现象，适用于多段翼型数值计算的SSTk-ω两方程模型[15]。

GA(W)-1翼型为NASA兰利中心设计的经典低速高升力翼型，常用于通用飞机。文献[16]给出了基于GA(W)-1翼型设计得到的29%襟翼弦长富勒襟翼实验结果，以襟翼偏角15°和30°时为算例验证本文计算方法和网格生成策略。计算条件：翼型弦长0.61 m，基于翼型弦长雷诺数为2.2×106，马赫数为0.154。图3给出了计算和实验升力系数对比结果，线性段计算和实验结果基本重合，失速迎角和最大升力系数偏大，但随襟翼偏角变化趋势与实验值符合较好。图4给出了5°迎角下计算和实验压力分布对比曲线，计算和实验符合的很好，主翼和襟翼的吸力峰值也模拟的较为准确。综合以上分析，本文数值求解方法和网格生成策略的能够用于富勒襟翼气动性能评估。

图3 计算和风洞实验升力系数对比曲线 (Ma=0.154、Re=2.2×106)Fig.3 Comparison of computational and experimental lift coefficient with Ma=0.154、Re=2.2×106

图4 α=5°计算和风洞实验压力分布对比曲线Fig.4 Comparison of computational and experimental pressure distributions at α=5°

2 富勒襟翼多目标优化

2.1 优化流程

如图5所示，单纯以线性段升力(α1)或最大升力(α2)为目标进行优化，分别会导致最大升力(图中双点化线)或线性段升力大幅损失(图中点化线)，不满足使用需求，因此，需开展多目标优化设计来协调各状态的气动性能。在多目标优化设计时，通常有两种方法：1) 采用权重系数法，对每一个目标函数赋予权重系数χi，则各个子目标函数的线性加权和作为多目标优化时的目标函数，从而把多目标优化问题转化为单目标优化问题，权重系数根据各项性能的重要程度合理选取，主观性较强，无法得到完整的权衡解，它的解对权系数十分敏感，而权系数的确定又带来很大的经验性。2) 求解Pareto解集方法亦即直接采用多目标优化算法进行优化。

图5 多段翼型单目标和多目标优化结果示意图Fig.5 Comparison of results between multi-objective and single-objective optimization

本文采用第二种方法，优化算法采用快速非支配排序遗传算法[17](Fast and Elitist Nondominated Sorting Genetic Algorithm，NSGA Ⅱ)，NSGA Ⅱ是由Deb等人于2002年在非支配排序遗传算法(Nondominated Sorting Genetic Algorithm，NSGA)基础上改进得到。NSGA Ⅱ算法有效地避免了NSGA中存在的计算复杂性，缺少了精英保存策略，收敛速度慢，参数σshare难以设定等问题，有着很好的收敛速度和鲁棒性，已成为多目标优化领域的基准算法之一。

基于NSGA Ⅱ优化算法构建富勒襟翼多目标优化设计流程如图6所示。为缩短优化时间，富勒襟翼气动评估模块基于曙光集群系统采用分布并行计算方式，一个富勒襟翼构型利用1计算节点(8CPUs)计算，5.1万网格完成两个迎角计算评估耗时约5.2 h。

图6 富勒襟翼多目标优化设计流程Fig.6 Flowchart of the multi-objective optimization process of Fowler flap

2.2 富勒襟翼优化及分析

以GA(W)-1翼型为基本翼型，保持主翼弦长为0.96c，襟翼弦长为0.30c，以富勒襟翼外形和缝道参数为优化变量，进行典型着陆构型优化设计，对于每个构型，考虑两个状态：‘飞行’状态(DP1，即使用迎角)和接近最大升力系数的大迎角下状态(DP2)。每个设计点采用固定迎角形式，评估DP1和DP2的估值函数，同时检查DP1和DP2的一些气动约束。本算例DP1和DP2分别为6°和13°。计算条件：Ma=0.091，基于弦长c=2.0677 m和标准大气条件Re=4.4×106。

优化目标：

Maxf1(x)=CL,α=6°

Maxf2(x)=CL,α=13°

约束条件：

CL,α=6°≥CL,α=6°@Baseline

CL,α=13°≥CL,α=13°@Baseline

设计变量和取值范围见表2，其中δf每隔0.5°取一个值，每代种群有36个个体，总代数为50，总共完成1800个富勒襟翼构型计算评估，18计算节点下耗时约8.7 h。

表2 优化变量及其范围Table 2 List of design variables and ranges

图7给出优化结束后，富勒襟翼的Pareto前沿面，共计124个优化构型，相比初始构型，前沿面优化构型迎角6°和13°下升力系数都有所增加，沿着Pareto前沿面由构型OPT1到OPT2，迎角6°时升力系数越来越大，反之，迎角13°升力系数越来越大，OPT3为综合迎角6°和迎角13°升力性能的优化构型。

图7 优化结果Fig.7 Result of optimization

图8给出了Pareto前沿面富勒襟翼外形控制参数分析结果，可以看出，各个最优构型襟翼前缘半径控制参数基本一样，并且接近其取值范围上限，说明前缘半径越大升力系数越大；各个最优构型襟翼外形点4控制参数差别很小，紧密地分布在其拟合曲线附近，而点3控制参数分布较为发散，说明点4襟翼外形控制参数对富勒襟翼气动性能影响较大，亦即襟翼可控外形部分后部外形对富勒襟翼升力影响较前部外形大。

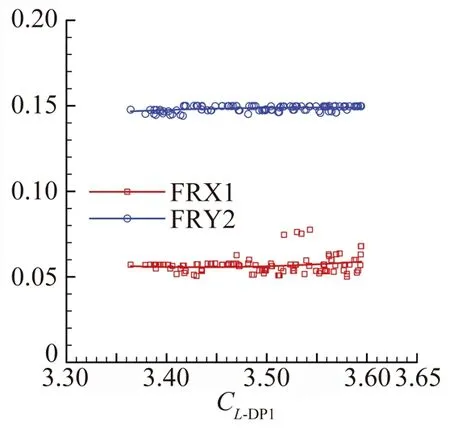
(a) FRX1 and FRY2

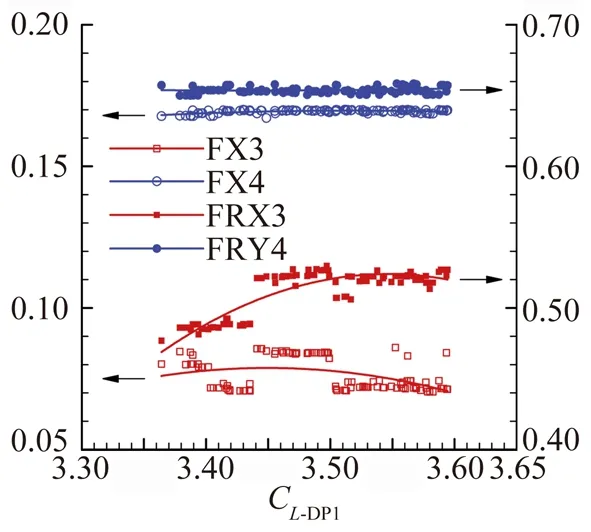
(b) FX3 FX4 FRY3 and FRY4

图9给出了Pareto前沿面富勒襟翼缝道参数分析结果，可以看出襟翼偏角差别很小，大多为39°和39.5°；缝道宽度紧密地分布在其拟合曲线附近，迎角6°升力系数随缝道宽度减小而增加，13°时随缝道宽度增加而增加，而搭接量分布较为发散，并且变化较小，说明缝道宽度对富勒襟翼升力性能影响较大。

(a) Design point 1

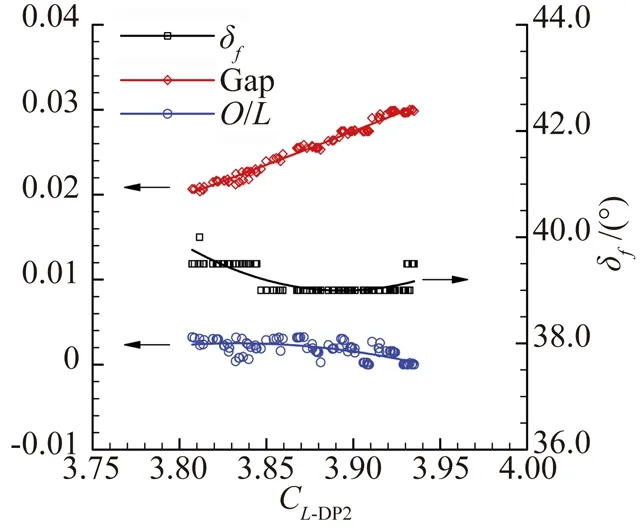
(b) Design point2

表3给出了富勒襟翼典型优化构型对应优化参数及设计点升力系数对比结果，图10给出了富勒襟翼典型优化构型外形对比。相比基本构型，优化构型前缘半径明显增加，头部厚度增加，中部厚度略有减小，升力系数有明显增加，其中迎角6°升力系数最大增加7.03%(OPT2)，13°迎角升力系数最大增加3.42%(OPT1)；从图11富勒襟翼典型优化构型升力系数随迎角变化曲线可以看出，构型OPT1失速迎角与基本构型相当，有最大的最大升力系数，线性段增加较小，而构型OPT2线性段升力系数增加较大，但其失速迎角减小约1°，最大升力系数增加较小，构型OPT3升力曲线相比基本构型基本成向上平移趋势。实际工程应用时，一般来说构型OPT1和OPT2并非最佳选择，而是根据需求，从Pareto前沿面优化构型中选择线性段升力系数和最大升力系数都有较大增加的构型，并根据侧重点不同择优选取，如构型OPT3，其迎角6°和迎角13°升力系数分别增加4.67%和1.95%。

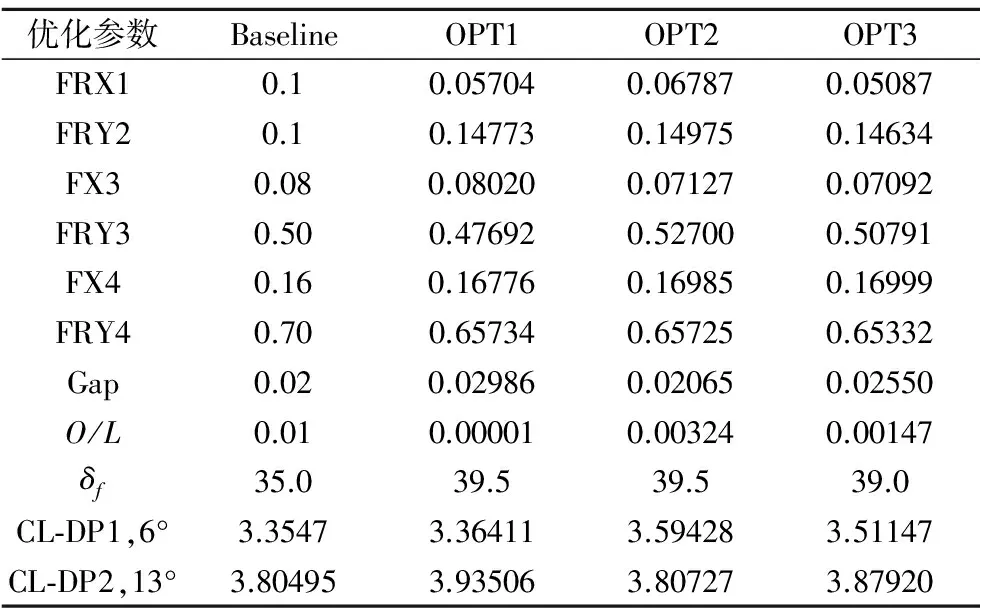
表3 典型优化构型设计参数对比Table 3 Pareto optimal design variable values for typical optimized solutions

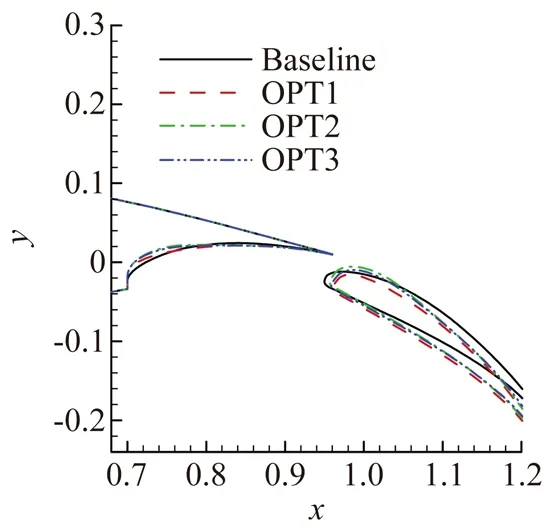
图10 富勒襟翼典型优化构型外形对比Fig.10 Comparison of typical optimized flap shape

图11 富勒襟翼典型优化构型升力系数随迎角变化曲线Fig.11 Comparison of lift coefficient of typical optimized flap configurations

3 结 论

1) 本文建立的富勒襟翼多目标优化设计方法，能够同时优化襟翼外形、缝道宽度、搭接量和襟翼偏角，提高线性段和大迎角升力性能；以GA(W)-1为基准翼型，优化得到的Pareto前沿面构型最大使迎角6°和13°升力系数增加7.03%和3.42%，并且效率高，鲁棒性强，适用于通用飞机富勒襟翼优化设计。

2) Pareto前沿面优化构型参数影响分析表明，富勒襟翼头部半径越大升力越大，襟翼可控外形部分后部外形对富勒襟翼升力影响较前部外形大，缝道宽度对富勒襟翼升力性能影响较搭接量大。

[1]Chen Y C, Li Y L, Ye J K, et al. Study progress about high-lift system of C919 airplane[J]. Advances in Aeronautical Science and Engineering, 2010, 1(1): 1-5. (in Chinese)陈迎春, 李亚林, 叶军科, 等. C919飞机增升装置工程应用技术研究进展[J]. 航空工程进展, 2010, 1(1): 1-5

[2]Reckzeh D. Aerodynamic design of the high-lift-wing for a megaliner aircraft[J]. Aerospace Science and Technology, 2003, 7: 107-119

[3]Van Dam C P. The aerodynamic design of multi-element high-lift systems for transport airplanes[J]. Progress in Aerospace Sciences, 2002, 38: 101-144

[4]HU W M. General aviation aircraft[M]. Beijing: Aviation Industry Press, 2008. (in Chinese)通用飞机[M]. 北京: 航空工业出版社, 2008

[5]Sangho Kim, Juan J Alonso, Antony Jameson. Design optimization of high-lift configurations using a viscous continuous adjoint method[R]. AIAA 2002-0844

[6]Haruka Nakayama, Hyoung-Jin Kim, Kisa Matsushima, et al. Aerodynamic optimization of multi-element airfoil[R]. AIAA 2006-1051

[7]Benini E, Ponza R, Massaro A. High-lift multi-element airfoil shape and setting optimization using multi-objective evolutionary algorithms[J]. Journal of Aircraft, 2011, 48(2): 683-696

[8]Huang J T, Gao Z H, Zhao K. Aerodynamic optimization of multi2airfoil based on MADS method and chimera technology[J]. Acta Aerodynamica Sinica, 2010, 28(4): 405-409. 黄江涛, 高正红, 赵轲. 基于MADS算法与嵌套网格技术的多段翼型优化设计方法研究[J]. 空气动力学学报, 2010, 28(4): 405-409

[9]Xun K L, Sun G. Subsection evolution optimal design of multi-element airfoil parameters based on the conservative chimera technique[J]. Acta Aerodynamica Sinica, 2011, 29(3): 374-379. (in Chinese)徐康乐, 孙刚. 基于守恒型嵌合体技术的多段翼型缝道参数分段进化优化设计研究[J]. 空气动力学学报, 2011, 29(3): 374-379

[10]Bai J Q, Liu N, Qiu Y S, et al. Optimization of multi-foil based on RBF mesh deformation method and modified particle swarm optimization algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12): 2701-2715. (in Chinese)白俊强, 刘南, 邱亚松, 等. 基于RBF动网格方法和改进粒子群优化算法的多段翼型优化[J]. 航空学报, 2013, 34(12): 2701-2715

[11]Ni A X, Zhang Y F, Chen H X. An improvement to NSGA-II algorithm andits application in optimization design of multi-element airfoil[J]. Acta Aerodynamica Sinica, 2014, 32(2): 252-257. (in Chinese)倪昂修, 张宇飞, 陈海听. NSUA-II算法的改进及其在多段翼型缝道参数优化中的应用[J]. 空气动力学学报, 2014, 32(2): 252-257

[12]Aircraft Design Handbook Total Editorial Board. Aircraft design handbook 6 aerodynamic design[M]. Beijing: Aviation Industry Press, 2002: 67-78 (in Chinese). 《飞机设计手册》总编委会. 飞机设计手册(第6册): 气动力设计[M]. 北京: 航空工业出版社, 2002: 67-78

[13]Boer A, Schoot M S, Faculty H B. Mesh deformation basedon radial basis function interpolation[J]. Computers and Structures, 2007, 85(11-14): 784-795

[14]Lin Y Z, Chen B, Xun X. Radial basis function interpolation in moving mesh technique[J]. Chinese Journal of Computational Physics, 2012, 29(2): 191-197. (in Chinese)林言中, 陈兵, 徐旭. 径向基函数插值方法在动网格技术中的应用[J]. 计算物理, 2012, 29(2): 191-197

[15]Rumsey C L, Ying S X. Prediction of high lift: review of present CFD capability[J]. Progress in Aerospace Sciences, 2002, 38: 145-180

[16]Wentz W H, Seetbaram H C. Development of a Fowler flap system for a high performance general aviation airfoil[R]. NASA CR-2443, 1974

[17]Deb K. A fast and elitist multiobjective genetic algorithm: NSGA Ⅱ[J]. Evolutionary Computation, IEEE Transaction on, 2002, 6 (2): 182-197.

Multi-objective optimization of Fowler flap on general aircraft

WEI Chuang1,*, ZHANG Tiejun1, LIU Tiezhong2
(1. Aero Science Key Lab of High Reynolds Aerodynamic Force at High Speed, AVIC Aerodynamics Research Institute, Shenyang 110034, China; 2. Aero Science Key Lab of High Reynolds Aerodynamic Force at Low Speed, AVIC Aerodynamics Research Institute, Harbin 150001, China)

A multi-objective optimization problem is presented to deal with a Fowler flap used in high-lift devices of general aircraft. The purpose is to enhance its aerodynamic performance by searching for optimal shape and setting parameters for the flap. The procedure driven by the genetic algorithm based on non-dominated sorting (NSGA II) method, elliptic equations, and RBF mesh deformation method is used to automatically generate the Fowler flap shape and compute meshes. Navier-Stokes solver is used for aerodynamic performance evaluation by distributed parallel computing that reduces optimization time cost. The Fowler flap optimization design based on GA(W)-1 airfoil is carried out to improve the lift coefficient in linear section of the lift curves(in the range lower than angle of attack 6°) and the maximal lift coefficient (near angle of attack 13°). The whole optimization process takes about 8 hours. The final Pareto optimal solutions are presented, and the correlation between design variables of the optimal airfoils is discussed. Compared with the baseline configuration, the maximal increments in lift coefficient at angle of attack 6° and 13° are 7.03% and 3.42%, respectively. These optimal results validate the high efficiency of the design optimization system proposed in this paper.

Fowler flap; multi-objective optimization; genetic algorithm based on non-dominated sorting (NSGA-II); Pareto optimal solutions

0258-1825(2017)04-0572-07

2017-04-02;

2017-06-15

魏闯*(1984-)，男，工程师，研究方向：气动优化，数值计算. E-mail：agangood@sina.com

魏闯, 张铁军, 刘铁中. 通用飞机富勒襟翼多目标优化[J]. 空气动力学学报, 2017, 35(4): 572-578.

10.7638/kqdlxxb-2017.0070 WEI C, ZHANG T J, LIU T Z. Multi-objective optimization of Fowler flap on general aircraft[J]. Acta Aerodynamica Sinica, 2017, 35(4): 572-578.

V211.3

A doi: 10.7638/kqdlxxb-2017.0070