基于粒子群算法的大型宾馆客房智能分配算法设计
2017-09-03甘肃机电职业技术学院王鹏亮
甘肃机电职业技术学院 王鹏亮
中国农业银行天水分行 裴海瑞
基于粒子群算法的大型宾馆客房智能分配算法设计
甘肃机电职业技术学院 王鹏亮
中国农业银行天水分行 裴海瑞
本文简要的介绍了离子群算法的思想和数学模型,紧跟着阐述了现在大型宾馆管理系统中存在的主要问题,重点论述了应用离子群算法对原有宾馆管理算法进行改进,简化系统运行,提高宾馆运营管理,提高经济效益。
组合规划;笛卡尔积;解域空
1.引入
进入21世纪,我国经济发展水平明显加快,人们对生活的质量有了更高的追求,外出旅游做为一种新型消费模式促使旅游业高速发展,也促使酒店宾馆等服务业蓬勃高速发展。而今很多大型宾馆在系统管理中存在一些问题,如当住店人过多或是宾馆房间太多的情况下,给顾客分配房间需要很长的时间,这就给顾客带来不便,更降低了宾馆的收益和竞争能力。如何实现宾馆管理智能化、现代化,提高客房资源的分配率,提升管理水平是当前大型宾馆发展急需解决的问题。
2.解决思路
宾馆客房的分配是一个典型的NP完全问题,也是一个多目标、多约束的空间调度分配问题。该问题会随着住店顾客的人数增多或是宾馆客房的增加,使客房的分配难度成倍的增加。其问题本身的难度决定了算法设计的困难性。粒子群(Particle Swarm Optimization,PSO)算法是一种群智能算法,它是一种适合求解多约束、多变量、多目标问题的进化算法,其原理简单、收敛性好、搜索效率高易实现。本文将PSO算法应用于客房分配问题算法的设计上,对客房分配算法进行优化。
3.PSO算法的原理和数学描述

下面给出粒子速度和粒子位置的更新迭代公式:

其中,参数ω(惯性权重ω∈(0,1)),r表示第 i个粒子在R维解域空间中对应的维数,表示第i个粒子的速度,c1和c2表示学习因子(又叫做加速因子,通常 c1=c2=2),1)的随机数,表示第i个粒子搜索到的最优值,表示整个群体在一次迭代中搜索到的最优值,表示第i个粒子的当前位
5.结束语

图1为粒子群在解域空间中搜寻最优解过程的示意图,n1,n2表示粒子群中的任意两个搜寻粒子。

图1 粒子群搜寻最优解移动示意图
4.客房分配问题中PSO算法设计
在客房分配问题中应用PSO算法进行排课算法设计,每个顾客为搜寻粒子,整个宾馆的房间为解域空间,每个满足要求的客房都代表了一个优化问题的可行解,下面应用PSO算法对排课问题进行算法设计:
(1)客房分配问题种群初始化。根据顾客人数和顾客住房要求确定搜索粒子数量和客房类型、输入客房数量,而后对顾客粒子均匀分散在解域空间中,等待搜索目标信息。
(2)建立一个立体三维空间坐标轴,应用三维空间对客房分配问题建模,根据客房数目、时间段次数和客房价位多少对三维坐标各坐标轴进行分割,则整个三维空间就被分割成了许多的小立方体,且把所有小立方体的初值设置为0,表示没有入住。三维空间中的每个小立方体代表一个迭代的顾客粒子,而且顾客粒子采用三维编码方式记录自身所搜索到的信息值。
(3)根据顾客要求确定入住客房类型,并且确定各入住房价,客房分配从底层向高层逐层分配,客房入住类型相同则尽量连号分配。
(4)顾客粒子在解域空间中按照时间段T和优先级选取相应的客房M进行分配。M一旦确定客房价位P也随之确定。这样一个顾客粒子就在解域空间中搜索到了的可行解G(T,M,P),即完成了一位顾客的客房分配任务。凡是三维空间中被分配了的客房小立方体都用1(有顾客入住)标注。然后继续执行步骤⑷直至所有顾客粒子都搜寻到可行解,然后比较可行解的相对最优解。
经过以上4个步骤,实现了客房分配问题中PSO算法设计和应用,完成了初始的客房分配任务。根据三维空间坐标中的立方体标注图如图2所示,可以准确获取顾客粒子的初始状态、分布情况及其规模大小。
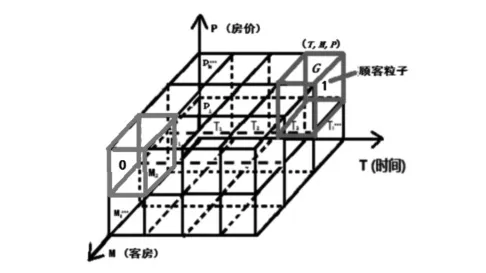
图2 客房分配标注示
本文针对大型宾馆查询系统客房查询存在的问题,引入PSO算法,对客房查询算法进行了设计,简化系统运行,提高宾馆运营管理,提高经济效益。
[1]江菱.宾馆客房管理系统分析与设计[D].云南大学,2013.
[2]代航阳.基VB的宾馆客房管理系统设计[D].电子科技大学,2006.
[3]郑宇军.C#语言程序设计基础[M].清华大学出版社,2011.
王鹏亮(1979—),男,甘肃天水人,工学硕士,甘肃机电职业技术学院讲师,主要研究方向为计算机应用技术教学。
裴海瑞(1982—),女,甘肃天水人,理学硕士,中国农业银行职员,中级职称,主要研究方向数学应用。
